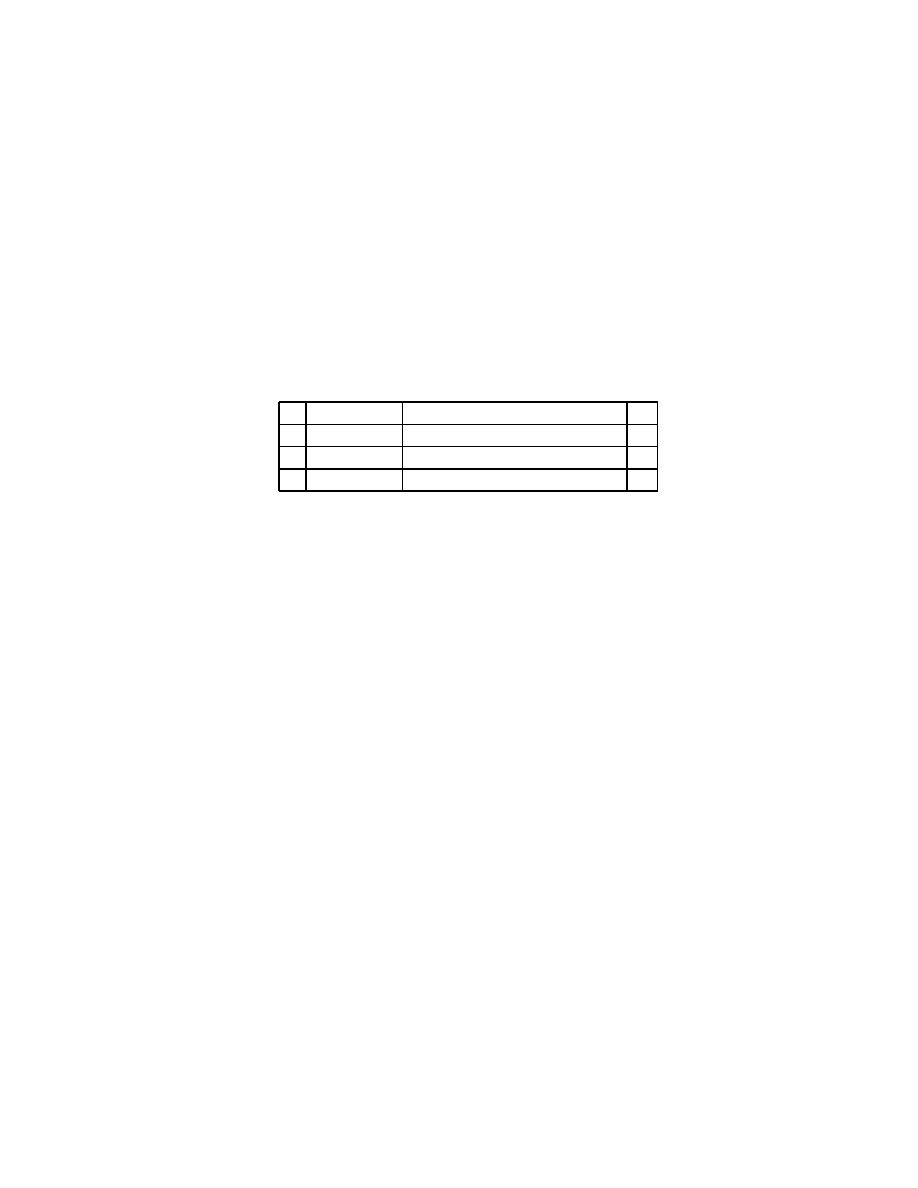
Architektura komputerów - ´cwiczenia - lista 2

1. Standard IEEE obsługuje cztery schematy zaokr ˛aglania: symetryczne do parzystej (ang. round-

to-nearest-even), obci˛ecie (ang. truncate), zaokr ˛aglanie w kierunku dodatnim (do

) i ujem-

nym ( do

). Oblicz ´sredni standaryzowany bł ˛ad zaokr ˛aglenia dla ka˙zdego z nich.

2. Znajd´z ostateczne postacie dla schematów zaokr ˛aglania wymienionych w poprzednim zadaniu

w nast˛epuj ˛acych przypadkach :

s Wykładnik

Znacznik

G

0 00011111 11111111111111111111111 1
0 11111110 11111111111111111111111 1
1 11111110 11111111111111111111111 1

3. Opieraj ˛ac si˛e na wynikach uzyskanych w poprzednim zadaniu przedstaw zalety schematu za-

okr ˛aglania symetrycznego do parzystej. Podaj tak˙ze wady tego schematu (z punktu widzenia
implementacji), które mog ˛a by´c usuni˛ete poprzez adaptacj˛e schematu zaokr ˛aglania symetrycz-

nego do nieparzystej.

4. Wykonaj poni˙zsze działania dla ka˙zdego schematu zaokr ˛aglania obsługiwanego przez standard

IEEE :

5. Po dodaniu dwóch znormalizowanych liczb pojedynczej precyzji

i

wynik był równy

.

Czy to implikuje

?

6. (a) Porównaj bł ˛ad powstaj ˛acy podczas obliczania iloczynu czterech liczb wykonywanego sze-

regowo jako

!

"$#

%$#

'&$#

z bł˛edem dla implementacji równoległej

(!

"$#

(%

&$##$)

Wska˙z metod˛e generuj ˛ac ˛a mniejszy bł ˛ad dla iloczynu

*

liczb.

(b) Powtórz zadanie zawarte w poprzednim punkcie dla sumy. Czy mo˙zna uzyska´c mniej-

sze bł˛edy, je´sli wiadomo, ˙ze liczby s ˛a uło˙zone według warto´sci, np.: od najmniejszej do

najwi˛ekszej ?