pytania egzaminacyje z fizyki odpowiedzi

WYKAZ ZAGADNIEŃ Z FIZYKI.

Fizyka jako ścisła nauka przyrodnicza.

Wielkości fizyczne i ich jednostki (Układ SI) Definicja wielkości fizycznych.

Definicje m, s, kg, A. K.

Wielokrotności i podwielokrotności (m,



, n, p, d, h, k, M, G,T)

Podstawy Mechaniki i Termodynamiki.

Opis ruchu.

Pojęcie ruchu i jego rodzaje.

Względność ruchu.

Pojęcie odległości – długości.

Ruch prostoliniowy i krzywoliniowy. b)

Układy współrzędnych. Układ współrzędnych prostokątnych. Układ współrzędnych

sferycznych.

Długość i szerokość geograficzna.

Kinematyka punktu – wektorowy opis różniczkowy.

Wektor położenia.

10. Droga i tor. (m, km, mila morska)
11. Definicja prędkości. (m/s, km/godz, węzły)
12. Definicja przyspieszenia.
13. Przyspieszenie styczne i normalne.
14. Przyspieszenie ziemskie.
15. I zasada dynamiki.
16. Ruch jednostajny.
17. I zasada dynamiki Newtona.
18. Ruch jednostajny.
19. Wykresy prędkości.
20. Wykresy drogi jako całki z prędkości
21. II zasada dynamiki Newtona
22. Pojęcie i definicja siły (N).
23. Ruch jednostajnie zmienny
24. Wykresy prędkości i przyspieszenia.
25. Droga jako całki z prędkości w ruchu zmiennym.
26. Równanie ruchu punktu materialnego.
27. Wektorowe, różniczkowe równanie ruchu.
28. Ruch jednowymiarowy: swobodny spadek ciała III zasada dynamiki.
29. Oddziaływanie ciał.
30. III zasada dynamiki Newtona.
31. Wzajemność oddziaływań.
32. Grawitacja i prędkości kosmiczne.
33. Prawo powszechnej grawitacji.
34. Przyspieszenie ziemskie a masa Ziemi.
35. Satelity i 1, 2 i 3 prędkość kosmiczna.
36. Opis ruchu obrotowego bryły sztywnej.
37. Bryła sztywna, jej ruch postępowy i obrotowy.
38. Opis ruchu obrotowego



)

39. Równanie ruchu bryły sztywnej.
40. Moment bezwładności.
41. Równanie ruchu bryły sztywnej.
42. Moment bezwładności punktu, walca i obręczy.
43. Praca i energia oraz zasady zachowania.
44. Pojęcie pracy i energii oraz mocy.
45. Definicja pracy (opis całkowo – wektorowy, J).
46. Definicja mocy i jednostki (W, KM).
47. Energia a praca.

48. Energia kinetyczna i potencjalna.
49. Zasada zachowania energii.
50. Energia kinetyczna w ruchu postępowym.
51. Energia kinetyczna w ruchu obrotowym – energia rotacyjna.
52. Energia potencjalna ciężkości.
53. Zasada zachowania energii (Prz: w swobodnym spadku ciała).
54. Oscylator harmoniczny.
55. Rozwiązanie równania ruchu oscylatora harmonicznego.
56. Równanie ruchu oscylatora harmonicznego.
57. Rozwiązanie tego równania dla drgań swobodnych.
58. Energia oscylacji.
59. Energia potencjalna sprężystości.
60. Energia kinetyczna, potencjalna i całkowita oscylatora.
61. Drgania wymuszone i tłumione.
62. Równanie ruchu oscylatora tłumionego i jego rozwiązanie
63. Wykres drgań tłumionych.
64. Oscylator z siłą wymuszającą.
65. Rezonans
66. Ruch falowy i podstawy akustyki.
67. Opis matematyczny fali płaskiej.
68. Matematyczny opis jednowymiarowej fali bieżącej.
69. Wykres zmienności amplitudy fali w czasie i przestrzeni.
70. Długość, częstotliwość, okres a prędkość fali.
71. Interferencja fal.
72. Fala stojąca. I
73. nterferencja fal jako efekt sumowania dwu fal.
74. Fala stojąca jako interferencja fali padającej i odbitej.
75. Dźwięk jako fala podłużna.
76. Fala poprzeczna a fala podłużna.
77. Wysokość, natężenie i barwa dźwięku
78. Rozprzestrzenianie się dźwięku w ośrodkach.
79. Prędkość dźwięku w gazach, cieczach i ciałach stałych..
80. Podstawy akustyki i hydroakustyki.
81. Prędkość dźwięku w powietrzu, wpływ temperatury i jej rozkładu.
82. Prędkość dźwięku w wodzie, wpływ uwarstwienia wód morskich.
83. Opis ruchu płynów.
84. Statyka płynów.
85. Ciśnienie i prawo Archimedesa.
86. Ciśnienie hydrostatyczne (jednostki ciśnienia, Pa, bar)
87. Prawo Archimedesa.
88. Pływanie i stateczność ciał pływających.
89. Równanie ciągłości dla cieczy i gazów.
90. Prawo zachowania masy w przepływach.
91. Równanie ciągłości dla cieczy.
92. Równanie ciągłości dla gazów.
93. Równanie Bernuliego
94. Zachowanie energii w przepływach.
95. Równanie Bernuliego
96. Ciśnienie statyczne, dynamiczne i całkowite.
97. Lepkość płynów.
98. Definicja lepkości i jednostki.
99. Wpływ lepkości na przepływy.
100. Zasady termodynamiki.
101. 0 zasada termodynamiki.
102. Cząsteczkowa budowa materii a stan termiczny ciał.
103. Temperatura – skale.
104. Zmiany właściwości ciał ze zmianą stanu termicznego – rozszerzalność.
105. Skala Celsjusza temperatury.

106. Bezwzględna skala temperatur (K).
107. I zasada termodynamiki.
108. Energia wewnętrzna ciał.
109. Równoważność pracy i ciepła.
110. Prawo zachowania energii.
111. I zasada termodynamiki.
112. Pojemność cieplna ciał.
113. Ciepło właściwe masowe i molowe.
114. Bilans cieplny.
115. II zasada termodynamiki.
116. Możliwości i ograniczenia zamiany ciepła na pracę.
117. II zasada termodynamiki.
118. Naturalne procesy termodynamiczne w przyrodzie a II zasada.
119. Entropia.
120. Sprawność termodynamiczna.
121. Sprawność zamiany ciepła na pracę.
122. Sprawność termodynamiczna – silnik idealny.
123. Cykl Carnotta Termodynamiczna definicja temperatury.
124. III zasada termodynamiki.
125. Ograniczenia przekazywania energii w niskich temperaturach.
126. III zasada termodynamiki.
127. Niemożliwość osiągnięcie zera w bezwzględnej skali temperatur.
128. Bezwzględna skala temperatury.
129. Zero w bezwzględnej skali temperatur a cząsteczkowa budowa materii.
130. Właściwości gazu doskonałego.
131. Kinetyczna teoria gazu doskonałego.
132. Model gazu doskonałego.
133. Wymiana pędu i energii cząsteczek gazu ze ścianką naczynia.
134. Ciśnienie gazu.
135. Równanie stanu gazu doskonałego.
136. Temperatura jako miara energii kinetycznej cząsteczek gazu.
137. Zasada ekwipartycji energii.
138. Właściwe ciepło molowe gazu a budowa cząsteczek.
139. Równanie stanu i przemiany gazu doskonałego.
140. Przemiana izotermiczna
141. Przemiana izochoryczna Cv.
142. Przemiana izobaryczna. Cp.
143. Równanie Mayera.
144. Przemiana adiabatyczna.



145. Cykl Carnotta przemian gazu doskonałego.
146. Zmiany stanu skupienia materii.
147. Przemiany fazowe.
148. Wykres T(Q).
149. Ciepło przemiany.
150. Izotermy z uwzględnieniem zmian stanu skupienia.
151. Wykres p(V).
152. Parametry krytyczne gazu.
153. Wykres fazowy V(T), punkt potrójny dla wody.
154. Stan skupienia a oddziaływania międzycząsteczkowe.
155. Rodzaje i zasięg oddziaływań międzycząsteczkowych.

Zjawiska elektromagnetyczne.
Elektryczne aspekty budowy materii.
Elektryzowanie ciał.
Elektron.
Ładunek elektryczny.

Elektryzowanie ciał jako efekt wymiany elektronów.
Ładunek elementarny.

Prąd elektryczny.
Amper.
Definicja ampera absolutnego.
Natężenie prądu a ładunek elektryczny (C)
Oddziaływania elektryczne.
Prawo Coulomba.

Oddziaływanie ciał naelektryzowanych.
Prawo Coulomba.
Pole elektrostatyczne.
Natężenie pola elektrostatycznego.

Potencjał. pola elektrostatycznego.
Napięcie. (V)
Pole elektrostatyczne ładunku punktowego i kuli naelektryzowanej
Pojemność i energia ciał naelektryzowanych
Pojemność elektryczna ciał (F).
Energia ciała naelektryzowanego.
Kondensator płaski.
Energia pola elektrycznego

Prawa Ohma dla prądów.
Prawo Ohma.
Opór elektryczny.
Opór właściwy.
Prawa Kirchoffa.
Prawa zachowania ładunku a I prawo Kirchoffa.
Prawa zachowania energii a II prawo Kirchoffa.
Magnetyzm

a) Oddziaływania magnetyczne.
Oddziaływania magnetyczne w przyrodzie.
Magnetyzm Ziemski.
Elektromagnetyzm jako nierozdzielność zjawisk elektrycznych i magnetycznych
b) Pole indukcji magnetycznej.
Wektor indukcji magnetycznej.
Siła Lorentza.

Skutki magnetyczne prądu.
Prawo Biotta – Savarta.
Pole magnetyczne wokół przewodnika prostego.
Prawo Ampera.
Indukcja elektromagnetyczna.

Prawo indukcji elektromagnetycznej Faradaya.
Prawa Maxwella i fale elektromagnetyczne.
Uogólnienie praw Faradaya i Ampera.

Uogólnienie praw dla obwodów na prawa dla pól.
Prawa Maxwella.
Wzajemne powiązania zjawisk elektrycznych i magnetycznych.
Rozchodzenie się zaburzeń pola elektrycznego lub magnetycznego.
Fale elektromagnetyczne i ich widmo.
Fale elektromagnetyczne jako efekt wzajemnej generacji pół elektrycznych i magnetycznych
przez dowolne zaburzenie pola elektrycznego lub pola magnetycznego.
Widmo fal elektromagnetycznych.
Natura światła.

Światło jako fala elektromagnetyczna.
Falowa natura światła.
Prawo odbicia i załamania światła a zasady Huygensa i Fermata.

Dyfrakcja i interferencja światła.
Widmo a barwy.
Podczerwień i ultrafiolet.
Zakres widmowy światła widzialnego.

Długość fali a barwa światła.

Barwy proste i zlożone
Promieniowanie ultrafioletowe.
Promieniowanie podczerwone.
Promieniowanie ciała doskonale czarnego.
Widmo promieniowania ciała doskonale czarnego.
Rozkład widmowy promieniowania ciał stałych.

Wykresy widm dla różnych temperatur.
Prawa Wiena i Stefana Boltzmana.
Prawo przesunięć maksimum promieniowania z temperaturą. (Wiena)
Temperatura a zdolność emisyjna ciał promieniujących. (Pr.Stefana – Boltzmana)
Kwantowy postulat Plancka
Kwantowe założenie Plancka.
Prawo Plancka.
Kwantowa natura światła.
Zjawisko fotoelektryczne.
Natężenie fotoprądu i energia fotoelektronów.
Kwantowe założenie Einsteina i Prawo zachowania energii.
Kwantowe założenie Einsteina.
Prawo zachowania energii dla zjawiska fotoelektrycznego.
Właściwości kwantowe światła.
Fotony. (E

, m

)

Struktura materii.

Rozwój poglądów na budowę materii.
(Modele atomu: Thomsona i Bohra).
Rola elektronu w wymianie energii promienistej.
Promieniowanie jako fala emitowana przez elektrony.
Oscylatorowy model atomu Thomsona.
Elektrony jako elektryczne oscylatory harmoniczne – dipole.
Doświadczenia Rutheforda i jego model.
Rozpraszanie szybkich elektronów przez materię.
Rozpraszanie cząstek



przez materię.

Jądrowy model atomu Rutheforda i jego wady.
Postulaty Bohra i jego model atomu wodoru.

Kwantowanie orbit elektronów.
I postulat Bohra.
Kwantowa wymiana energii przy zmianie orbity.
II postulat Bohra.
Atom wodoru wg. Bohra.
Serie widmowe atomu wodoru.
Uzupełnienia Sommerfelda i spin elektronu.
Struktura linii widmowych.
Subtelna struktura linii widmowych.
Orbity eliptyczne.
Liczby kwantowe.
Dopuszczenie orbit eliptycznych i kwantowanie ich kształtów.
Główna i poboczna liczba kwantowa Atom w polu magnetycznym
Rozszczepienie linii widmowych w polu magnetycznym.
Moment magnetyczny elektronu.
Kwantowanie przestrzenne.
Magnetyczna liczba kwantowa.
Spin elektronu.
Doświadczenie Sterna – Gerlacha.

Własny moment magnetyczny elektronu.
Spin i spinowa liczba kwantowa.
Zakaz Pauliego.
Układ okresowy pierwiastków

Widma atomowe i cząsteczkowe.
Systematyka widm atomowych.

Stany energetyczne atomu a liczby kwantowe
Układ poziomów energetycznych atomu i jego obsadzenie przez elektrony.
Reguły wyboru.
Przejścia między poziomami energetycznymi.
Przejścia dozwolone i niedozwolone.
Reguły wyboru dla liczb kwantowych.

Stany metatrwałe.
Rezonans elektronowy.
Przejścia przy zmianie spinu.
Rezonans elekrtronowy.

Rezonans jądrowy.
Wpływ jądra na poziomy energetyczne.
Rezonans jądrowy.
Wpływ oddziaływań na linie widmowe.

Oddziaływania międzycząsteczkowe a stany energetyczne.
Prędkość w termicznym ruchu cząsteczek i Efekt Dopplera.
Termiczne i ciśnieniowe rozszerzenie linii widmowych
Widma cząsteczkowe.

Oddziaływania między atomami w cząsteczkach.
Stany rotacyjne i oscylacyjne.
Rozmycie linii widmowych w pasma.
Widma cząsteczkowe.

Widma ciał stałych.
Pasma energetyczne elektronów w ciałach stałych.
Pasmo walencyjne i pasmo przewodnictwa.
Wpływ domieszek na poziomy energetyczne.

Widma promieniowania ciał stałych.
Emisja spontaniczna i wymuszona.
Emisja spontaniczna w naturalnym promieniowaniu ciał.
Wymuszona emisja fotonów.

Lasery i spójność światła.
Zasada działania laserów.
Spójność i polaryzacja światła laserowego..

Struktura jądra atomowego i przemiany jądrowe.
Składniki jądra.
Liczba atomowa i masowa.
Właściwości protonów i neutronów.

Liczba masowa i atomowa a skład jądra.
Defekt masy i energia jądrowa.
Defekt masy a liczba porządkowa.
Energia wiązania jądra.

Rola mezonów.
Przemiany jądrowe.
Naturalny rozpad promieniotwórczy.
Promieniowanie



Prawo rozpadu naturalnego.
Okres połowicznego rozpadu
Sztuczne przemiany jądrowe.

Rozszczepienie jąder. Synteza jądrowa.
Energetyka jądrowa.
Reaktory atomowe.
Energia termojądrowa.
Ochrona radiologiczna.
Szkodliwość promieniowania jądrowego.
Dozymetria.
Kwarki. Hipoteza kwarków.

Systematyka cząstek elementarnych.
Problem złożoności cząstek elementarnych.

Kwarki Problem cząstki elementarnej.
Rozwój poglądów na strukturę materii i hipotezy.

Właściwości ciał stałych..
Sieci krystaliczne
Pasma energetyczne termiczne, elektryczne i magnetyczne właściwości ciał stałych.

Półprzewodniki.
Złącza p-n Tranzystory.

... I. 12 Wielkości fizyczne i ich jednostki (Układ SI) Definicja wielkości fizycznych.

długość odległość

metr

masa

kilogram

czas

sekunda

prąd elektryczny

amper

temperatura

kelwin

liczność materii

mol

światłość

kandela

I.13 Definicje m, s, kg, A. K.

metr (m) - jest to długość równa 1 650 763,73 długości fali w próżni promieniowania

odpowiadającego przejściu między poziomami 2p

a 5d

atomu

Kr (kryptonu 86 )

Sekunda (s) – jest to czas równy 9 192 631 770 okresom promieniowania

odpowiadającego przejściu między dwoma poziomami struktury nad subtelnej stanu
podstawowego atomu izotopu cezu

133

Kilogram (kg) – jest to masa międzynarodowego wzorca tej jednostki, cylindrowi

platynowo-irydowemu umieszczonemu we Francji.

Amper (A) – jest to prąd elektryczny nie zmniejszający się , który płynąc w dwóch

równoległych prostoliniowych, nieskończenie długich przewodach o przekroju kołowym

znikomo małym, umieszczonych w próżni w odległości 1 m od siebie – wywołałby między
tymi przewodami siłę 2

-7

N na każdy metr długości.

Kelwin (K) – jest to 1/273,16 temperatury termodynamicznej punktu potrójnego wody.

I.14. Wielokrotności i podwielokrotności (m,



, n, p, d, h, k, M, G,T)

eksa

peta

tera

giga

mega

kilo

hekto

deka

decy

-1

centy

-2

mili

-3

mikro



-6

nano

-9

piko

-12

femto

-15

atto

-18

II. 1 Opis ruchu.

II. 2 Pojęcie ruchu i jego rodzaje.

Ruchem nazywamy następującą w czasie zmianę położenia ciała względem wybranego
układu odniesienia.

II. 3 Względność ruchu.

W zależności od układu odniesienia ciało może znajdować się w spoczynku i w ruchu.

II. 4 Pojęcie odległości – długości.

II. 5 Ruch prostoliniowy i krzywoliniowy.
Ruch prostoliniowy to taki ruch dla którego torem jest linia prosta a krzywoliniowy to taki

gdzie torem jest krzywa.

II. 6 Układy współrzędnych. Układ współrzędnych prostokątnych. Układ współrzędnych

sferycznych.
W celu ścisłego opisania ruchu przyjmujemy układ odniesienia składający się z 3

prostopadłych osi Ox, Oy, Oz. W układzie tym za pomocą współrzędnych x, y, z można
wyznaczyć położenie dowolnego punktu przestrzeni.
Układ współrzędnych sferycznych, jeden z podstawowych układów współrzędnych.
Pierwszym układem współrzędnych sferycznych był układ współrzędnych astronomicznych,

umożliwiający określanie położenia ciał na sferze niebieskiej. W układzie tym podaje się dwa
zorientowane kąty: kąt θ pomiędzy wyróżnioną płaszczyzną (horyzontem, ekliptyką,
równikiem niebieskim, w zależności od rodzaju układu) a prostą wiodącą od obserwatora do
ciała niebieskiego oraz kąt



pomiędzy płaszczyzną wybranego (konwencjonalnie) koła

wielkiego, prostopadłego do wyróżnionej płaszczyzny, a kołem wielkim przechodzącym
przez dane ciało. W układzie fizycznych współrzędnych sferycznych kąty te uzupełnia się
odległością R od obserwatora (początek układu współrzędnych sferycznych) do danego ciała.

Współrzędne sferyczne związane są ze współrzędnymi kartezjańskimi x, y, z następującymi
relacjami: x = R cos



cosθ, y = R sin



cosθ, z = sinθ.

II. 7 Długość i szerokość geograficzna.

Odległość kątowa określająca położenie danego miejsca na kuli ziemskiej. Długość
geograficzna to kąt pomiędzy południkiem ziemskim danego miejsca a płaszczyzną ozna-

czonego południka zerowego, za który przyjęto południk przechodzący przez Greenwich w
Anglii. Na równiku 10 dl. geogr. równa się w przybliżeniu 113 km. Szerokość geogr. to
odległość kątowa pomiędzy dowolnym punktem Ziemi a równikiem, mierzona na płn. lub na
płd. Po łuku ziemskim; jest ona równa kątowi między płaszczyzną równika a pionem w

danym punkcie; podaje się ją w stopniach, minutach, sekundach. Każda minuta odpowiada 1
mili morskiej długości 1,85 km.

II. 8 Kinematyka punktu – wektorowy opis różniczkowy.

II. 9 Wektor położenia.

Położenie punktu można wskazać także za pomocą wektora łączącego początek układu (punkt
0) z punktem M. Jest to wektor położenia lub nazywany jest też wektorem wodzącym.

II. 10 Droga i tor. (m, km, mila morska)

Linia ciągła, którą tworzą kolejne położenia rozpatrywanego punktu poruszającego się ciała,
nazywa się torem punktu, a określony odcinek toru przebyty przez poruszający się punkt w
określonym czasie – drogą s poruszającego się punktu.
Mila morska - jednostka miary odległości na morzu równa 6080 stopom, tj. 1852,8 m.

II. 11 Definicja prędkości. (m/s, km/godz, węzły)

Można wyodrębnić prędkość średnią i chwilową: P śr. Jest to wektorowa wielkość fizyczna
równa stosunkowi przesunięcia



r do czasu



t, w którym to przesunięcie nastąpiło. Potocznie

określa się to jako stosunek drogi jaką przebyło ciało , do czasu w którym ta droga została

przebyta. To pojęci jest jednak mało precyzyjne ponieważ mierzona jest w dość dużym
przedziale czasu. P ch. Jest to prędkość ciała w danej chwili, mierzona w przedziale czasu
spełniającym warunek v=



t -> 0

Węzeł, jednostka prędkości stosowana w żegludze, równa 1 mili morskiej na godzinę (1,85
km/godz.). Nazwa wiąże się ze stosowaniem logu ręcznego: liczba supłów przepuszczanych
przez rękę w czasie 3 s - przy ich rozmieszczeniu na loglinie co 154 cm, tj. co 5 stóp - równa
jest prędkości statku w węzłach.

II. 12 Definicja przyspieszenia.

Jeżeli przyrosty prędkości w ruchu jednostajnie zmiennym są wprost proporcjonalne do

czasu, to stosunek tych dwóch wielkości ma wartość .stałą. Ten stały stosunek przyrostu

prędkości (v - vo) do czasu t, w którym przyrost zachodzi. nazywa się przyśpieszeniem ruchu
jednostajnie zmiennego i oznaczany jest literą a.

II. 13 Przyspieszenie styczne i normalne.

Ciało poruszające się po torze krzywoliniowym ze stałą wartością prędkości doznaje
przyspieszenia prostopadłego do wektora prędkości o zwrocie do środka krzywizny toru.

Przyspieszenie to ma nieco inny charakter od dotąd poznanego i dla odróżnienia nosi nazwę

przyspieszenia dośrodkowego (normalnego). Oznaczamy je a

Rozważania powyższe dotyczyły ruchu ze stałą wartością prędkości. A co będzie, gdy

wartość prędkości ulegnie zmianie ? W takim przypadku wystąpi jeszcze drugie

przyspieszenie, które ma kierunek styczny do toru. Obliczamy je podobnie jak dla ruchu

prostoliniowego. Przyspieszenie to nosi nazwę stycznego i oznaczamy je a

. Całkowite

przyspieszenie jest sumą wektorową obu przyspieszeń

II. 14 Przyspieszenie ziemskie.

Przyśpieszenie, którego doznają ciała swobodnie spadające, zwane przyśpieszeniem

ziemskim g, jest zależne od szerokości geograficznej i od wysokości nad poziomem morza,

zmienia się jednak w bardzo małych granicach. W fizyce stosuje się najczęściej normalną

wartość przyśpieszenia ziemskiego g

= 9,80665 m/sek

odpowiadającą szerokości

geograficznej 45° i mierzoną na poziomie morza. Natomiast w obliczeniach technicznych

przyjmuje się przybliżoną wartość

g = 9,81 m/sek

= 981 cm/sek

Kierunek przyśpieszenia jest oczywiście pionowy, zwrócony ku środkowi kuli ziemskiej,
ponieważ w tym kierunku zachodzą przyrosty prędkości.

II. 16 I zasada dynamiki.

Jeżeli na ciało działa układ sił równoważących się wzajemnie, to pozostaje ono w spoczynku
lub w ruchu prostoliniowym, jednostajnym.
Oznacza ona, że jeśli na ciało nie działa żadna niezrównoważona siła i początkowo było ono

nieruchome, to pozostaje nadal nieruchome, jeżeli zaś początkowo poruszało się w pewnym
kierunku z pewną prędkością, to ruch jego się nie zmieni, tj. ciało porusza się nadal w tym
samym kierunku i z tą samą prędkością.

II. 17 Ruch jednostajny.

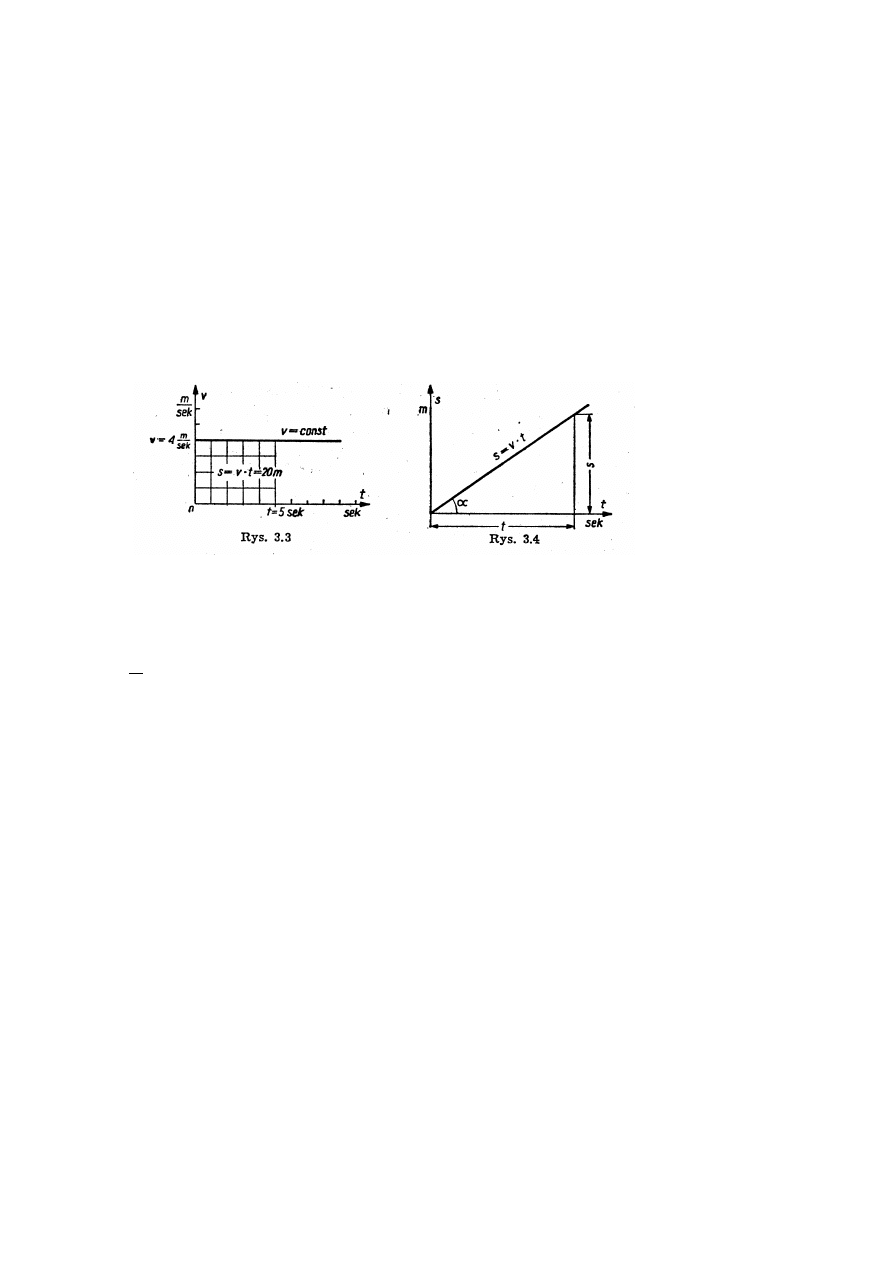
To taki ruch, w którym przebywana droga jest wprost proporcjonalna do czasu ruchu, co
oznacza że w różnych, dowolnie małych odstępach czasu punkt materialny przebywa drogi
równe.

II. 19 Wykresy drogi jako całki z prędkości II. 18 Wykresy prędkości.

II. 20 II zasada dynamiki Newtona.

Niezrównoważona siła F, działając na ciało, nadaje mu przyspieszenie a, które jest wprost
proporcjonalne do wielkości siły i odwrotnie proporcjonalne do masy m ciała, a skierowane
tak samo jak siła

II. 21 Pojęcie siły.

W zjawiskach ruchu spotykamy się z takimi wzajemnymi oddziaływaniami na siebie ciał, w
wyniku których ciało nieruchome zostaje wprawione w ruch, ciało poruszające się ulega
zatrzymaniu bądź też ruch ciała zostaje w pewien sposób zmieniony, np. co do kierunku lub
wartości prędkości. Oddziaływania takie nazywają się s i ł a m i.
W celu łatwiejszego opisu zjawisk pomija się w mechanice znikome zmiany wymiarów i
kształtów ciał pod wpływem działania sił, przyjmuje że pozostają one nie zmienione. Inaczej
mówiąc zastępuje się ciała rzeczywiste uproszczonym modelem, zwanym ciałem doskonale
sztywnym.
Siły dzieli się na zewnętrzne, które działają z zewnątrz na ciało (np. nacisk, siła przyciągania
itp.) oraz we w nętrzne, występujące wewnątrz ciała i wywołane wzajemnym oddziaływaniem
na siebie jego cząsteczek (np. siła skurczająca rozciągniętą sprężynę itp.). Siły zewnętrzne

mogą działać przy bezpośrednim zetknięciu się ciał albo też na odległość.
Siły zewnętrzne dzielą się ponadto na czynne, które dążą do wywołania ruchu, jego zmiany
lub odkształceń, oraz bierne, które występując w miejscach podparcia lub zawieszenia
przeciwdziałają siłom czynnym. Si1y bierne pojawiają się przy tym w chwili przyłożenia sił

czynnych i znikają, gdy przestają one działać. Tak np. ciężar żeliwny spoczywający na
podłożu wywiera na nie pod wpływem siły czynnej, a mianowicie ciężaru G, nacisk
prostopadły (normalny) N, ale ponieważ jest on nieruchomy podłoże musi oddziaływać na
niego siłą bierną skierowaną ku górze i równoważącą ciężar. Siłę, z jaką podłoże oddziałuje

na spoczywające na nim ciało nazywa się reakcją R.
Doświadczenia wykazują że skutek działania siły (np. ruch ciała) zależny jest od kierunku jej
działania – siła jest więc wektorem. Siłę określają następujące cechy:

* wielkość siły – można wyrazić liczbowo podając jej wartość w odpowiednich jednostkach
(N);

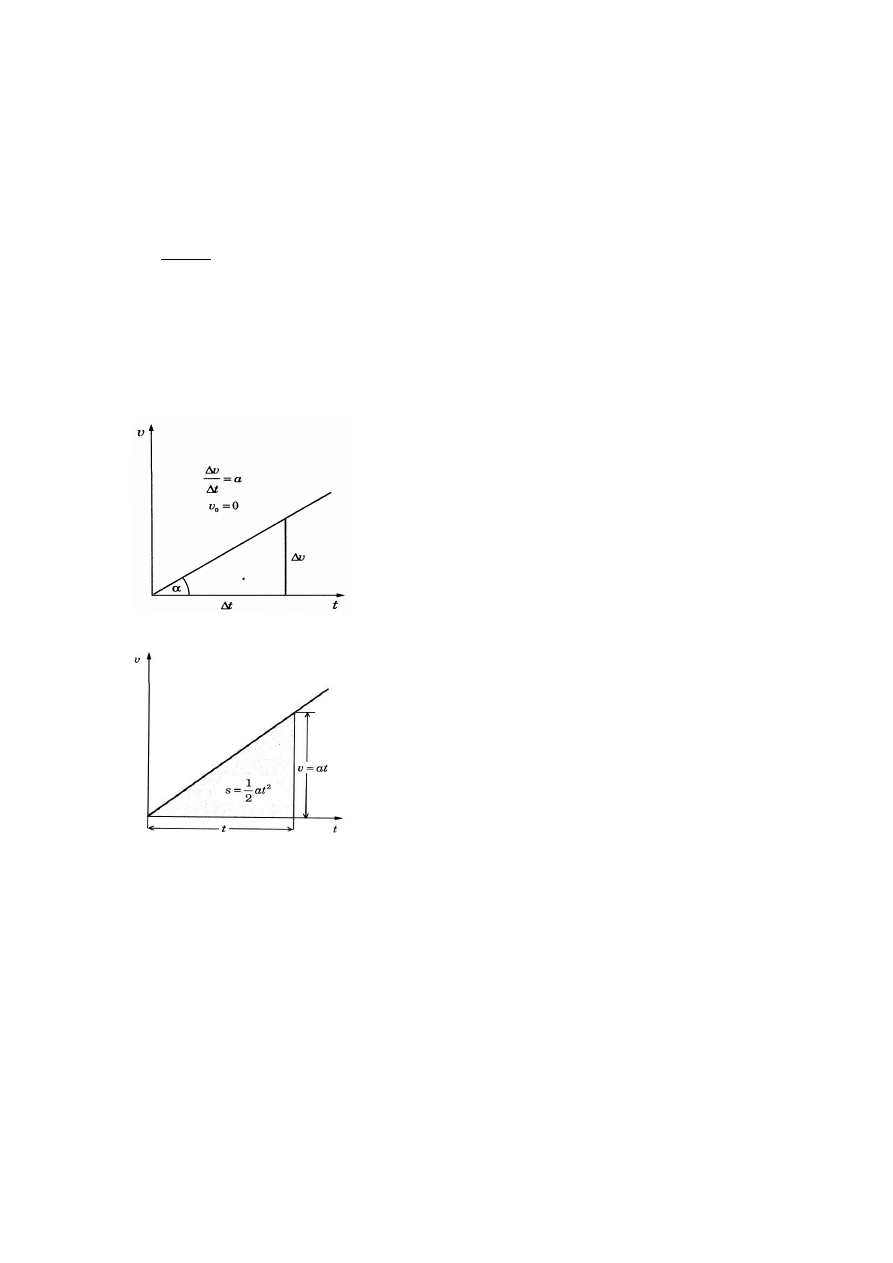
* kierunek działania siły – określa się przez podanie kąta, który tworzy on z pewnym
kierunkiem umownym;

* skutek działania siły – jest zależny nie tylko od jej wielkości i kierunku, ale również od linii
działania.
* dla niektórych sił (np. siły ciężkości), podaje się jeszcze punkt przyłożenia, oznacza się go
liczbowo przez podanie współrzędnych odpowiednich dla danego układu.

II. 23 Definicja siły (N)

Jednostką siły w układzie Si jest Niuton (N), to jest taka siła, która masie 1kg nadaje
przyspieszenie 1 m/s

1 N = 1

kg * m

II. 22 Ruch jednostajnie zmienny

Często zdarza się ruch zmienny tego rodzaju, że przyrosty prędkości są wprost proporcjonalne
do czasu tzn. w równych dowolnie małych odstępach czasu przyrosty prędkości są

jednakowe. Taki ruch nazywa się jednostajnie zmiennym. Oczywiście mogą być ruchy
jednostajnie przyśpieszone, jednostajnie opóźnione.

II. 23 Wykresy prędkości i przyspieszenia.

II. 24 Droga jako całki z prędkości w ruchu zmiennym.

II. 25 Równanie ruchu punktu materialnego.

Jeżeli punkt materialny porusza się ruchem jednostajnym z prędkością v w czasie t, to drogę
przebytą s wyrazi równanie s = v * t. Jeżeli w chwili rozpoczęcia obserwacji (t=0) ciało
poruszające się ruchem jednostajnym postępowym znajduje się w odległości s

od przyjętego

punktu odniesienia – równanie ruchu jednostajnego ciała względem tego punktu przyjmie
postać

s = s

+ v * t

Jeżeli w chwili rozpoczęcia obserwacji (t=0) ciało poruszające się ruchem prostoliniowym
jednostajnie zmiennym znajduje się w odległości s

od przyjętego punktu odniesienia i ma

prędkość v

– równanie ruchu ciała, określające jego położenie względem tego punktu,

przyjmie postać

s = s

+ v

t + at

Jeżeli natomiast początek obserwacji odpowiada chwili początkowej ruchu w której v

=0,

równanie ruchu jednostajnie zmiennego przyjmie uproszczoną postać

s = at

Prędkość - v = v

+ a * t

II. 26 Wektorowe, różniczkowe równanie ruchu.

II. 27 Ruch jednowymiarowy: swobodny spadek ciała

Wszystkie ciała w próżni spadają jednakowo szybko.

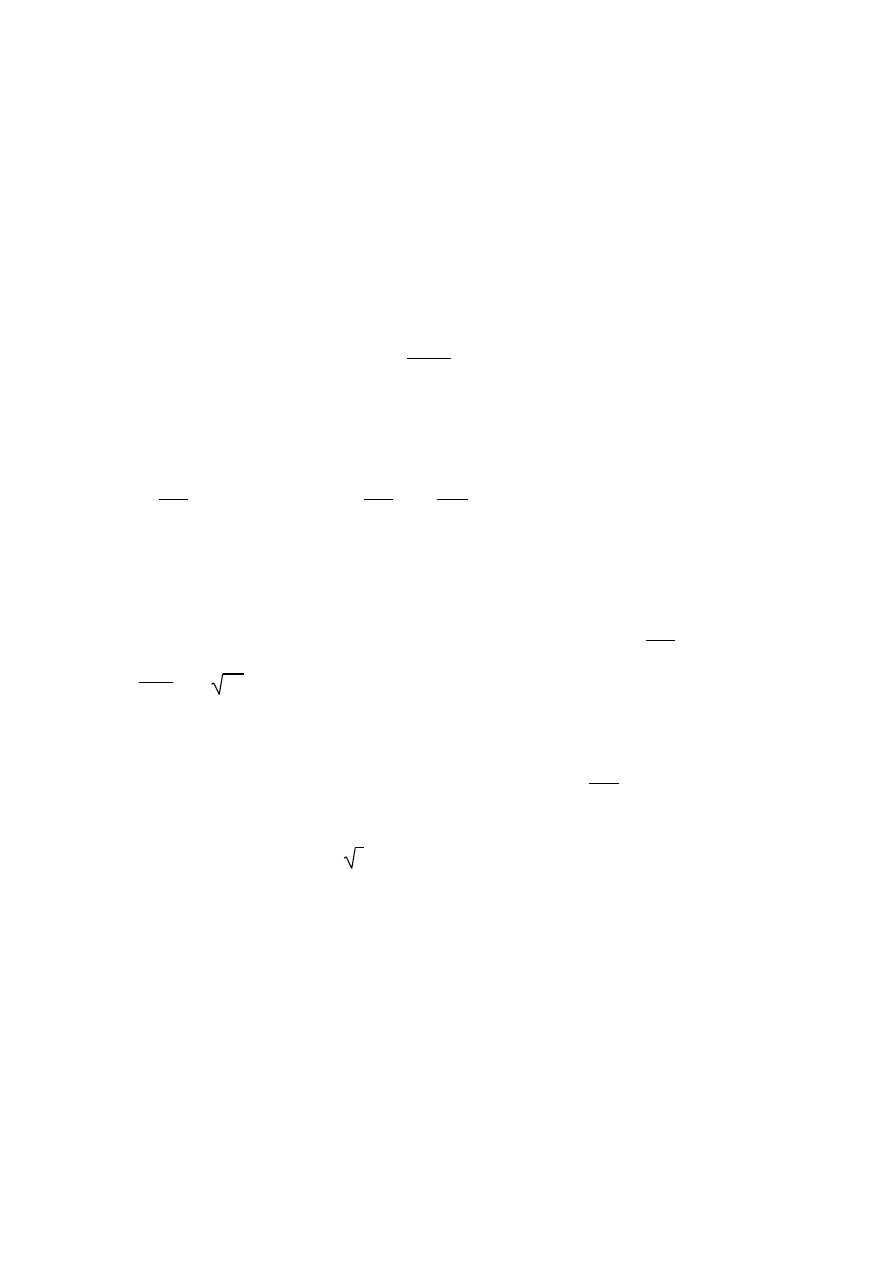
Droga przebyta przez ciało swobodnie spadające jest wprost proporcjonalne do kwadratu
czasu spadania, czyli że ruch ciał swobodnie spadających jest ruchem jednostajnie

przyspieszonym, ze stałym przyspieszeniem, niezależnym od ciężaru ciała.

II. 28 Oddziaływanie ciał.

II. 29 III zasada dynamiki Newtona.

Jeżeli ciało A działa na ciało B siłą, to ciało A siłą równą co do wartości, o takim samym
kierunku, lecz przeciwnym zwrocie.

II. 26 Wzajemność oddziaływań.

II. 27 Prawo powszechnego ciążenia.

Każde dwa ciała przyciągają się wzajemnie siłami grawitacji, których wartości są wprost

proporcjonalne do iloczynu mas tych ciał i odwrotnie proporcjonalne do kwadratu odległości

między środkami ich mas.

II. 28 Przyspieszenie ziemskie a masa Ziemi.

Przyspieszenie ziemskie to charakterystyczne przyspieszenie z jakim opadają wszystkie ciała
znajdujące się na powierzchni ziemi; g=9,81

. Siła z jaką ziemia przyciąga ciało (F

) jest

równa co do wielkości sile z jaką ciało przyciąga ziemię(F

)

= F

...(F=ma)... a [g=9,81]=

...M=

g R

i stąd masa ziemi M

=5,96*10

II. 29 Satelity i 1, 2 i 3 prędkość kosmiczna.

Pierwsza prędkość kosmiczna jest to prędkość jaką należy nadać ciału, stycznie do
powierzchni ziemi, aby obiegało ją tuż nad powierzchnią (przy założeniu braku atmosfery).

Krążący nad powierzchnią ziemi, ale poza zasięgiem atmosfery (ok. 160 km )satelita podlega

działaniu siły grawitacyjnej, która pełni tutaj rolę siły dośrodkowej F

=mg –

mg=

m v

- v= gR ; przy założeniach R=6370km, g=9,8

v=7,9km/s – taką prędkość

musiało by mieć ciało aby mogło obiegać ziemie tuż przy jej powierzchni nie spadając na nią
II prędkość kosmiczna to najmniejsza prędkość, którą należy nadać ciału wyrzucanemu z

ziemi, aby oddaliło się w nieskończoność. Jeżeli ciału znajdującemu się na powierzchni ziemi

nadamy energię kinetyczną spełniającą warunek : E

=0,5mv

= G

to będzie ono mogło

(pomijając opór atmosfery ziemi) opuścić obszar jej grawitacyjnego przyciągania. Ciało takie
staje się wtedy sztucznym satelitą słońca Wyliczoną w ten sposób prędkość v=

Error!

nazywa

się prędkością ucieczki. Jest ona 2 razy większa od I prędkości (11,19 km/s)
Niekiedy mówi się też o trzeciej prędkości kosmicznej, tj. prędkości, jaką trzeba nadać ciału

w pobliżu Ziemi, by opuściło ono Układ Słoneczny (wynosi ona 42 km/s w układzie
odniesienia względem Słońca.

II. 30 Opis ruchu obrotowego bryły sztywnej.

Podczas ruchu obrotowego bryły sztywnej wszystkie jej punkty (wyłączywszy oś obrotu)
zataczają okręgi o środkach leżących na osi obrotu. Podczas ruchu obrotowego każdy punkt
bryły sztywnej porusza się z taką samą prędkością kątową. Jeżeli prędkość kątowa ruchu

obrotowego nie jest stała, wprowadza się pojęcie przyspieszenia kątowego e; bryły sztywnej
(w dowohiej chwili jednakowe dla każdego punktu tej bryły).

II. 31 Bryła sztywna, jej ruch postępowy i obrotowy.

Bryłą sztywną nazywamy ciało, w którym odległość dwu dowolnie wybranych punktów nie
ulega zmianie, mimo działających na to ciało sił.
W ruchu postępowym odcinek łączący dowolne dwa punkty bryły sztywnej pozostaje
równoległy do swoich poprzednich położeń.

II. 32 Opis ruchu obrotowego



)

Ruchem obrotowym nazywa się taki ruch, w którym torami wszystkich punktów

poruszającego się dała są okręgi współśrodkowe, a ich środki nie biorące udziału w ruchu leżą

na jednej prostej zwanej osią obrotu. Drogi przebyte równocześnie przez punkty położone w

różnych odległościach od osi obrotu nie są jednakowe, ale tym większe, im większa jest ich

odległość od osi obrotu. Droga kątowa



- jest to kąt obrotu ciała wyrażony w radianach.

Droga kątowa charakteryzuje ruch obrotowy właściwiej niż droga liniowa, która jest różna dla

punktów różnie odległych od osi obrotu. Zgodnie z określeniem miary łukowej kąta, jako

stosunku odpowiadającego mu łuku do promienia (s łuk, r promień)



mamy s =



* r

Droga liniowa s dowolnego punktu obracającego się ciała jest równa iloczynowi drogi
kątowej



przez odległość r punktu od osi obrotu.

Stosunek drogi kątowej α do czasu t, w którym została ona zakreślona nazywamy

prędkością kątową w ruchu obrotowego.





Jednostką prędkości kątowej jest radian na sekundę

Rozróżnia się ruchy obrotowe jednostajne, w których prędkość kątowa jest wielkością stałą,
czyli zakreślona droga kątowa jest wprost proporcjonalna od czasu oraz – ruchy obrotowe

zmienne, w których ta zależność nie jest zachowana.
W technice miarą prędkości ruchu obrotowego jednostajnego jest prędkość obrotowa (ilość

pełnych obrotów wykonanych w jednostce czasu) Jednostką p o jest obrót na sekundę

lub

obrót na minutę

min

Prędkość liniowa v dowolnego punktu obracającego się ciała równa się iloczynowi prędkości
kątowej



przez odległość r danego punkt od osi obrotu v =



* r

Można wyodrębnić ruchy w których prędkość kątowa ( a zatem i obrotowa) nie są
wartościami stałymi. Występują one przy rozruchu i hamowaniu. Przyrost prędkości kątowej





są wprost proporcjonalne do czasu t, w którym ten przyrost zachodzi, jest dla

takiego ruchu wielkością stałą i nosi nazwę przyspieszenia kątowego.





Jednostką

przyspieszenia kątowego jest radian na sekundę do kwadratu (

), czyli takie przyspieszenie

które w czasie 1 sekundy powoduje przyrost prędkości 1 radiana na sekundę.
Przyśpieszenie liniowe a dowolnego punktu obracającego się ciała równa się iloczynowi
przyśpieszenia kątowego



przez odległość r danego punkt od osi obrotu a =



* r

II. 33 Równanie ruchu bryły sztywnej.

II. 34 Moment bezwładności.

Jeżeli ciało o masie m i bardzo małych wymiarach geometrycznych (punkt materialny) obraca
się dookoła punktu ) po kole o promieniu r z przyspieszeniem kątowym



, pod wpływem

działania nań momentu M=F*r, wówczas z 2 prawa Newtona F=m*a wypływa związek:
M=m*r



gdyż a=r*



Iloczyn m*r

= I nazywamy momentem bezwładności punktu materialnego m względem osi

obrotu O

II. 35 Moment bezwładności punktu, walca i obręczy.

Walec J



( d

3
4

)



Obręcz (pierścień o przekroju prostokątnym i kołowym ) J

1
2



ab R (4 R

)



(16 R

+ 3 a

)

II. 36 Zasady zachowania energii.

Suma energii kinetycznej i potencjalnej w układzie, na który nie działają siły zewnętrzne i nie
następuje w nim rozpraszanie energii wskutek działania sił, jest wielkością stałą.
Suma początkowa energii układu ciał + suma włożonych prac = suma końcowa energii
układu ciał

Suma włożonych prac = suma przyrostów energii układu

II. 37 Pojęcie pracy i energii.

Ciało mające zdolność wykonania pracy (np. zawieszone, napięte lub będące w stanie ruchu)

posiada energię, zaś zasób pracy W, którą to ciało może wykonać nazywamy jego energią
mechaniczną E. Energię mierzy się w jednostkach pracy.
Przekazywanie energii innym ciałom może przybierać różne formy. Jeżeli odbywa się ono w
sposób mechaniczny, czyli możliwy do opisania prawami mechaniki, to nazywa się pracą.
Drugim sposobem przekazu energii jest ciepło.

II. 38 Definicja pracy (opis całkowo – wektorowy, J).

Praca (W) – jest to iloczyn siły działającej F przez drogę s i cosinus kąta zawartego między
kierunkiem działania siły i kierunkiem ruchu. W = F*s*cos



w dynamice skalarna wielkość fizyczna W (L) zdefiniowana wzorem:

gdzie: F - siła działająca na ciało, wykonująca pracę wzdłuż drogi S, ds - nieskończenie
mały wektor styczny w każdym miejscu do drogi S.

Jednostką pracy jest (J) dżul. Jeden dżul jest równy pracy jaką wykonuje siła 1N na
drodze 1m; przy założeniu, że zwrot działającej siły jest zgodny ze zwrotem przesunięcia

(



=0).

1J = 1N * 1m

[J] =

kg m

Można przytoczyć 4 przypadki wartości pracy w zależności od kąta przyłożenia działającej

siły, względem kierunku przesunięcia jej punktu zaczepienia.



=0 – c os



=1 – W = F*s

2. 0 <



< 90

– W = F*s*cos



=90

– cos



= 0 – W = F*s*cos



= 0



=180

– cos



= -1 – W = F*s*cos



= W = - F*s

II. 39Definicja mocy i jednostki (W, KM).

Moc – jest to stosunek pracy W do czasu t, w którym ta praca została wykonana P =

Jednostką mocy jest wat. 1 wat jest równy mocy urządzenia, które w ciągu 1 sekundy

wykonuje pracę 1 dżula; 1W=

1kW = 1000W

KM – koń mechaniczny (z ang.) 1KM = 0,736 kW 1kW = 1,36 KM

II. 40 Energia kinetyczna i potencjalna.

Energia mechaniczna występuje w dwóch postaciach: jako energia potencjalna, którą
posiadają niektóre ciała w spoczynku (np. zawieszony ciężar, napięta sprężyna) lub energia
kinetyczna, którą obdarzone są ciała w ruchu (np. pędząca kula).

II. 41 Energia kinetyczna w ruchu postępowym.

E k Jeżeli stała siła F wprawia w ruch jednostajnie zmienny ciało o masie m udzielając mu na
drodze s prędkości v, to energia kinetyczna ciała spełnia równanie E

=W=F*s – ( II zasada

dyn Newtona F=m*a równanie ruchu jednostajnie zmiennego o prędkości początkowej v

i v=a*t to...) E

II. 42 Energia kinetyczna w ruchu obrotowym – energia rotacyjna.

Rozpatrzmy obecnie energię kinetyczną ciała, znajdującego się w ruchu obrotowym

jednostajnym. W tym celu załóżmy;, że tarcza o masie m złożona z bardzo dużej ilości

cząsteczek o masach m

, m

... m

. tak małych. że można je przyjąć za punkty materialne

obraca się dookoła osi przechodzącej przez jej środek ciężkości ze stałą prędkością kątową



Energię kinetyczną poszczególnych cząsteczek wyrazi równanie

k n

(podstawiając v



) E

k n



Energia kinetyczna całej tarczy jest

oczywiście sumą energii jej poszczególnych cząsteczek E



k n





- -





Wyrażenie



nazywamy momentem bezwładności J wirującej tarczy

względem osi obrotu

J =





Energia kinetyczna E

ciała obracającego się dookoła osi przechodzącej przez jego środek

ciężkości równa. jest połowie iloczynu momentu bezwładności tego ciała J względem osi

obrotu, przez kwadrat prędkości kątowej



Jednostką momentu bezwładności jest iloczyn jednostki masy przez kwadrat jednostki

długości, a więc kg*m

II. 43 Energia potencjalna ciężkości.

E p Ciało o masie m położone na wysokości h nad pewnym poziomem odniesienia (za który
przyjmuje się najczęściej powierzchnie kuli ziemskiej) posiada energię potencjalną położenia
(ciężaru).

=G*h

=m*g*h ponieważ spadając może wykonać pracę W=G*h

Energia potencjalna ciała jest równa iloczynowi ciężaru ciała przez wysokość położenia

II. 44 Oscylator harmoniczny.

Jest to wyidealizowany układ fizyczny - punkt materialny o masie m, na który działa siła
proporcjonalna do chwilowego wychylenia x od pewnego położenia równowagi.

II. 45 Równanie ruchu oscylatora harmonicznego.
x = A sin



- częstość kołowa ruchu (jeżeli punkt porusza się jednostajnie po

okręgu z prędkością kątową



to jego rzut porusza się ruchem harmonicznym z częstością

kołową



= 2



v =



gdzie T jest okresem, a v częstością ruchu. Wielkość A określa

wartość maksymalnego wychylenia ze stanu równowagi (x=A). Nosi ona nazwę amplitudy
ruchu harmonicznego.
Prędkość w ruchu harmonicznym (tak samo jak w kołowym) baza[





* r ; v =



* r

A=r po porównaniu ruchu kołowego i oscylacyjnego rzut tej prędkości na oś pionową to v =
v

cos





A cos





A cos



przyspieszenie – a = -



A sin



t ... a = -



II. 46 Rozwiązanie tego równania dla drgań swobodnych.

II. 47 Energia potencjalna sprężystości.

Występuje ona w przypadku napiętej sprężyny. Policzenie pracy jest tu trudniejsze, ponieważ
siła odkształcająca sprężynę nie jest stała, a wzrasta w zależności od wydłużenia sprężyny.
Dla zwykłych sprężyn siła jest proporcjonalna do wydłużenia, co można zapisać wzorem
F=k



r, gdzie k to stała sprężyny. Aby obliczyć pracę wykonaną podczas rozciągania sprę-

żyny, musimy znaleźć siłę średnią. Siła ta, rozciągająca sprężynę od



, jest średnią

arytmetyczną wartości siły na początku i na końcu rozciągania. F

śr

gdzie F

1-2



1-2

stąd praca wynosi W = F

śr



(



) = =



Otrzymaliśmy różnicę dwóch wyrażeń, które oznaczały stany związane z napięciem sprężyny.

Tak więc wielkość wyrażoną wzorem E



II. 48 Energia kinetyczna, potencjalna i całkowita oscylatora.

E = E

+ E

wyprowadzenie E

; v =



A cos



t ; [ m



= k –wyprowadzone z II

zasady Newtona i założenia przyspieszenia a = -



x ]

k
2

cos





k – jest współczynnikiem sprężystości (F=-kx) a



r- zmianą długości

odkształcanego ciała



r=x (x = A sin



k
2

sin



t po podstawieniu E=

II. 49 Drgania wymuszone i tłumione.

W wypadku gdy ruch oscylatora harmonicznego odbywa się bez tarcia, wtedy amplituda
ruchu jest stała. Stała jest także energia. Jeżeli nie podtrzymywać ruchu wahadła czy kulki na
sprężynie, to po pewnym czasie ruch ustanie. Energia oscylatora zostanie rozproszona,
zamieniona na energię wewnętrzną poruszającego się ciała i jego otoczenia. Ruch zbliżony do
harmonicznego, ale taki, w którym amplituda maleje w funkcji czasu, nazywamy ruchem
harmonicznym tłumionym. W tym ruchu amplituda maleje ale okres drgań pozostaje
wartością stała.
W ruchu harmonicznym wymuszonym wyróżniamy 3 rodzaje przypadków drgań w

zależności od częstości pobudzanej;

a) mniejszej od częstości własnej układu
b) równej częstości własnej układu
c) większej od częstości własnej układu

W przypadkach a i c obserwujemy ruchy o niezbyt wielkiej amplitudzie. Z reguły początkowo
kulka wykonuje ruchy dosyć nieregularne, po pewnym czasie zaczyna poruszać się
harmonicznie z częstością równą częstości wymuszającej i stałej amplitudzie.

Zupełnie inaczej zachodzi zjawisko, gdy częstość wymuszająca jest równa częstości własnej
układu. Wtedy amplituda drgań rośnie z czasem liniowo. Po chwili staje się bardzo znaczna,
kulka zaczyna "wyrywać się" trzymającym ją sprężynom. We wszystkich trzech wypadkach
mamy do czynienia z tak zwanym wymuszonym ruchem oscylatora. Przypadek b, kiedy częs-

tość drgań pobudzających jest równa częstości własnej układu, nazywamy rezonansem.

II. 50 Równanie ruchu oscylatora tłumionego i jego rozwiązanie

II. 51 Wykres drgań tłumionych.

Zależność wychylenia od czasu w ruchu harmonicznym tłumionym

II. 52 Oscylator z siłą wymuszającą.

Równanie : ma = - kx + F

przy założeniach że siła F

zależy sinusoidalnie od czasu

zgodnie ze wzorem F

= F

sin



t , układ nie jest rezonansem (



=/=



– częstość kołowa

siły wymuszającej =/=częstość kołowa własna układu.) i porusza się periodycznie z
częstością równą częstości siły wymuszającej



, a x = A sin



t. , przyspieszenie dane jest

wzorem; a = -



A sin



t to dochodzimy do wniosku że A(



) =

czyli że przy



(





0 ) ;





∞ co jest fizycznie niemożliwe !

II. 53

Rezonans

Zjawisko gwałtownego wzrostu amplitudy drgań układu mechanicznego lub elektrycznego

zachodzące, gdy częstość drgań wymuszających zbliża się do częstości drgań własnych.

II. 54 Ruch falowy i podstawy akustyki.

Ruch falowy jest zjawiskiem bardzo często występującym w przyrodzie. Jednym z

przykładów są fale na powierzchni cieczy: gdy na kałużę upadnie kropla deszczu, rozchodzi
się po niej zaburzenie w kształcie charakterystycznych okręgów. Bezustannie wykonują też
ruch falowy powierzchnie naturalnych zbiorników wodnych. Znamy też przykłady innych fal
mechanicznych: jeżeli poruszymy koniec swobodnie zawieszonego sznura czy łańcucha,

pojawia się na nim odkształcenie szybko "wędrujące" ku górze. Falami mechanicznymi są też
dźwięki rozchodzące się w powietrzu i innych ośrodkach materialnych.
Akustyką nazywamy naukę o zjawiskach dźwiękowych, tj. zjawiskach wyczuwalnych
zmysłem słuchu. Mają one charakter falowy, mianowicie wiążą się z powstawaniem i

rozchodzeniem się w powietrzu lub innym ośrodku sprężystym fali podłużnej, polegającej na
kolejnym zagęszczaniu i rozrzedzaniu warstw cząsteczek ośrodka, zwanej falą dźwiękową lub
głosową.

II. 55 Opis matematyczny fali płaskiej.

Jeżeli front fali ma postać płaszczyzny prostopadłej do kierunku rozchodzenia się fali to taka
fala nazywa się płaską.

Równanie sinusoidalnej fali płaskiej rozchodzącej się wzdłuż osi odciętych x. s = A cos[ω(t-
x
u

) + φ ]. Wielkość k =

nosi nazwę liczby falowej. Po przekształceniach k =

2π

λ . Tak więc

liczba falowa wskazuje na to, ile długości fal układa się na odcinku równym 2π metrów. Jest
to wielkość analogiczna do częstości kołowej, która wskazuje ile okresów mieści się na
odcinku czasowym równym 2π sekund. Ostatecznie s = A cos(ωt - kx + φ). Z tego wynika że

Drganie to jest funkcją harmoniczną s = A cos(ωt + α) α = φ- kx

II. 56 Matematyczny opis jednowymiarowej fali bieżącej.

II. 57 Wykres zmienności amplitudy fali w czasie i przestrzeni.

Wartość maksymalnego wychylenia fali nazywa się Amplitudą i oznacza się poprzez A.

II. 58 Długość, częstotliwość, okres a prędkość fali.

Im większa jest częstotliwość v pobudzającego ruchu harmonicznego, tym mniejsza jest
długość fali. Fala biegnie z określoną prędkością v. W ciągu jednego okresu T fala
przebiegnie odcinek struny równy długości fali λ. Dla ruchu jednostajnego s = vt, czyli w

naszym przypadku λ = vT. Związek między okresem T ruchu harmonicznego a jego

częstością v jest następujący T =

; a więc λ=

; lub v = λv. Ze wzoru wynika że długość fali

jest odwrotnie proporcjonalna do częstości fali v. Częstość zależy od długości jeżeli długość
fali jest mniejsza to częstość jest większa. Im większa jest prędkość fali, tym większa częstość

ruchu harmonicznego. Pojęcia okresu, długości, częstości, amplitudy fali mają sens tylko dla
fal sinusoidalnych

II. 59 Interferencja fal.

Rozpatrzmy pewien obszar przestrzeni, w którym dodają się dwie lub kilka fal. Jeżeli okaże

się, że intensywność drgania wypadkowego w dowolnym punkcie jest równi sumie

intensywności fal, to mówimy, że nie ma interferencji. Jeżeli jednak okaże się, że przy

nałożeniu fal następuje rozkład energii, tak że intensywność w jednych punktach jest większa

a w innych mniejsza od intensywności sumarycznej,- to mówimy, że występuje interferencja.

Tak więc interferencją nazywamy zjawisko rozkładu energii powstające w pewnych

określonych warunkach w wyniku zsumowania się amplitud dwóch lub kilku fal.

Stabilny w czasie obraz rozkładu intensywności, powstający w wyniku interferencji

nosi nazwę obrazu interferencyjnego.

Powstanie fali stojącej jest przykładem zjawiska interferencji. Stały w czasie układ węzłów i

strzałek jest typowym przykładem obrazu interferencyjnego.

II. 60 Fala stojąca.

Gdy biegnąca fala zostanie całkowicie odbita to suma fali początkowej i odbitej (które to się
na siebie nałożą) daje tzw. falę stojącą. . W odróżnieniu od fali biegnącej, w której wszystkie

punkty odbywają drgania o tej samej amplitudzie, lecz z opóźnieniem fazowym, w fali
stojącej wszystkie punkty drgają równocześnie, lecz z różny amplitudami. Obszary, w których
ośrodek znajduje się w spoczynku (amplitudy zerowe) noszą nazwę węzłów fali stojącej,
obszary zaś drgające z maksymalną amplitudą – noszą nazwę strzałek.

II. 61 interferencja fal jako efekt sumowania dwu fal.

Interferencją nazywamy nakładanie się fal przy czym wychylenie fali wypadkowej jest
algebraiczną sumą wychyleń fal składowych (zasada -superpozycji). W wyniku interferencji

fale mogą się wzmacniać (jeżeli ich fazy są zgodne) lub wygaszać (jeżeli ich fazy są
przeciwne).
Maksymalne wzmocnienie (maksimum interferencyjne) dwóch fal spójnych jest
obserwowane w punktach, w których różnica dróg (różnica odległości punktu od obu źródeł

nakładających się fal) równa jest całkowitej wielokrotności długości fali.
Maksymalne wygaszenie (minimum interferencyjne) dwóch fal jest obserwowane w
punktach, w których różnica dróg jest równa nieparzystej wielokrotności połówki długości
fali.

II. 62 Fala stojąca jako interferencja fali padającej i odbitej.

Fala stojąca powstaje w wyniku nałożenia się dwóch fal poruszających się w przeciwne
strony. Jedna z nich to fala wzbudzana przez źródło i rozchodząca się wzdłuż osi odciętych.
Równanie jej :ma postać s

= Acos (ωt – kx) Druga fala powstaje na skutek odbicia

pierwszej fali od przegrody. Ponieważ rozchodzi się ona w kierunku ujemnych wartości
osi odciętych, więc w równaniu należy zmienić znak przy współrzędnej. Prócz tego należy

uwzględnić fakt, że przy odbiciu faza fali może się zmienić. Dlatego też równanie fali odbitej
ma postać; s

= Acos (ωt + kx + φ) równanie fali stojącej zapiszemy w postaci

s = s

=Acos(ωt – kx) + (ωt + kx + φ) po wykonaniu elementarnych przekształceń

otrzymamy s = 2Acos(kx +

) cos(ωt +

) = Bcos (ωt +

), gdzie amplituda fali stojącej ma

postać B = 2Acos (kx +

)

II. 63 Dźwięk jako fala podłużna.

II. 64 Fala poprzeczna a fala podłużna.

Na powierzchni cieczy powstają fale, które nie są wywołane przez sprężystość ośrodka, lecz
przez siły napięcia powierzchniowego lub przez siły ciężkości (fale kapilarne i grawitacyjne).
Osobliwość tych fal polega na tym, że cząsteczki cieczy drgają w kierunku pionowym, fala
zaś rozchodzi się w płaszczyźnie poziomej. Jeżeli drgania cząsteczek ośrodka odbywają się
prostopadle do kierunku rozchodzenia się fal, to taka fala nosi nazwę fali poprzecznej
W ciałach stałych możliwe są zarówno fale podłużne jak i poprzeczne. Fala podłużna
powstaje w wyniku deformacji typu sprężenie lub rozrzedzenie - podobnie jak w cieczach lub

gazach (sprężystość objętości). Fala poprzeczna powstaje. dzięki właściwości sprężystości
postaci. Gazy i ciecze nie :mają sprężystości postaci i dlatego nie mogą w nich powstawać
fale poprzeczne.
Plaryzacja fali mechanicznej określa, jaki jest kierunek drgań cząsteczek (elementów ośrodka)

w stosunku do kierunku rozchodzenia się fali. Poznaliśmy
dwa podstawowe typy polaryzacji.

l. W fali podłużnej kierunek wychyleń jest równoległy do kierunku

rozchodzenia się fali.

2. W fali poprzecznej kierunek wychyleń jest prostopadły do kierunku rozchodzenia się

fali.

II. 65 Wysokość, natężenie i barwa dźwięku

Fizyczną miarą wysokości dźwięku jest częstotliwość drgań źródła dźwięku. Dźwięk jest tym

wyższy (cieńszy) im większa jest częstotliwość v, i odwrotnie. Granice słyszalności

dźwięków wynoszą v= 16 - 20 000 Hz.

Wysokość dźwięku można w przybliżeniu określić przez porównanie słuchem dwóch

dźwięków, z których jeden jest dźwiękiem wzorcowym o znanej częstotliwości. Do-

kładniejszych pomiarów dokonuje się przez wykreślenie na jednostajnie poruszającej się

taśmie, za pomocą przyrządu zwanego fonografem, wykresu drgań źródła dźwięku.

Natężenie jest cechą odróżniającą dźwięki silne od słabych. Fizyczną miarą natężenia

dźwięku jest natężenie fali głosowej w danym punkcie, określone równaniem

F * t

Fala przenosi energię od źródła, które ją wysyła. Wielkość tej energii równa jest pracy

zużytej na zakłócenie równowagi cząsteczek ośrodka sprężystego. Stosunek ilości
przenoszonej energii E do iloczynu powierzchni fali F przez czas t nosi nazwę natężenia fali.

Można udowodnić, że natężenie dźwięku jest wprost proporcjonalne do gęstości ośrodka,
kwadratu amplitudy i kwadratu częstotliwości drgań.

Dźwięki o jednakowej wysokości i jednakowym natężen1u, wydawane przez różne źródła,

różnią się od siebie. Różnice te spowodowane są charakterem drgań źródła i określają barwę

dźwięku. Wykreślając za pomocą fonografu wykresy drgań, odpowiadające różnym źródłom,

można się przekonać, że różnym kształtom wykresów odpowiadają różne barwy dźwięku

II. 66 Rozprzestrzenianie się dźwięku w ośrodkach.

Fale dźwiękowe nie rozchodzą się w próżni. Warunkiem powstawania i rozchodzenia się fal

dźwiękowych jest wystąpienie sprężystego ośrodka materialnego, w którym mogą być
wywołane drgania jego cząstek. Najczęściej spotykamy się ze zjawiskiem rozchodzenia się
fal dźwiękowych w powietrzu, chociaż mogą się one również rozchodzić w cieczach i ciałach
stałych.

II. 67 Prędkość dźwięku w gazach, cieczach i ciałach stałych..

Prędkość rozchodzenia się fali w powietrzu i innych gazach wyraża się wzorem v=

Error!

x – stosunek ciepła właściwego gazu pod stałym ciśnieniem do ciepła właściwego w stałej

objętości x =

; p – ciśnienie gazu; d – gęstość gazu.

Prędkość fali dźwiękowej w gazach zależy więc zarówno od ciśnienia jak i temperatury gazu,
ponieważ gęstość gazu jest funkcją temperatury. W warunkach normalnych w powietrzu v =
333m/s

W powietrzu poruszającym się, fale unoszone są razem z ośrodkiem i prędkość rozchodzenia
się fali i kierunku ruchu powietrza.
W ciałach stałych i cieczach v=

Error!

E – moduł sprężystości (ściśliwości) ośrodka.

II. 68 Podstawy hydroakustyki.

II. 69 Prędkość dźwięku w powietrzu, wpływ temperatury i jej rozkładu.
II. 70 Prędkość dźwięku w wodzie, wpływ uwarstwienia wód morskich.

II. 71 Opis ruchu płynów.
II. 72 Statyka płynów.

II. 73 Ciśnienie i prawo Archimedesa.

Jest to skalarna wielkość fizyczna równa stosunkowi wartości siły prostopadłej do

powierzchni na którą ona działa do wielkości tej powierzchni p=

p - ciśnienie; F – siła; s -

powierzchnia

II. 74 Ciśnienie hydrostatyczne (jednostki ciśnienia, Pa, bar)

Jest to ciśnienie wywierane przez nieruchomą ciecz, wywołane przez jej ciężar. Jest ono

wprost proporcjonalne do wysokości słupa cieczy i jej gęstości p = ςgh p – ciśnienie
hydrostatyczne; ς – gęstość cieczy; g – przyspieszenie ziemskie; h – wysokość słupa cieczy.
Ciśnienie nadanej głębokości zależy jedynie od grubości warstwy cieczy i od jej gęstości, nie

zależy od całkowitej masy cieczy ani od kształtu naczynia.

Prawo Pascala: Jeżeli ciśnienie P

jest wywierane na część powierzchni płynu, to rozchodzi

się ono jednakowo na wszystkie części powierzchni ograniczającej płyn.

1 Pa =

1 N

1 m

kg*m
s

- to takie ciśnienie jaki wywiera siła 1N na powierzchnię 1m

1 bar = 1000 mbr = 10

Pa.

II. 75 Prawo Archimedesa.

Ciało zanurzone w płynie (ciecz, gaz) traci pozornie na ciężarze tyle, ile waży płyn wyparty

przez to ciało. Innymi słowy: wypór, jakiemu podlega ciało zanurzone w płynie, równa się
ciężarowi płynu wypartego przez to ciało. F

=Vςg; F

–siła wyporu; V – objętość

zanurzonego ciała; ς – gęstość cieczy; g – przyspieszenie ziemskie.

II. 76 Pływanie i stateczność ciał pływających.

Ciało pływa całkowicie zanurzone jeżeli jego gęstość (ciężar właściwy) jest równa gęstości
cieczy.

Ciało tonie jeżeli jego gęstość jest większa gęstości cieczy, w której zostało zanurzone.
Ciało wypływa jeżeli jego gęstość jest większa gęstości cieczy. Po wypłynięciu ciało takie
pływa częściowo zanurzone, przy czym stosunek objętości zanurzonej części do całej jego
objętości jest równy stosunkowi gęstości ciała do gęstości cieczy.

Warunkiem pływania jest równowaga ciężaru i wyporu.

II. 77 Prawo zachowania masy w przepływach.

Równanie ciągłości strumienia wytłumaczyć można na przykładzie kanału o zmiennym

przekroju. W tym wypadku równania dla 3 dowolnych przekrojów tego kanału m

* w

;

* w

; m

* w

Gdy przepływ czynnika jest ustalony to strumień masy (masowe

natężenie przepływu) w każdym miejscu kanału jest jednakowy m

= m

. Wynika stąd

tzw. Równanie ciągłości strumienia

* w

czyli

S * w

= const

II. 78 Zachowanie energii w przepływach.

Energia kinetyczna czynnika E

m * w

; E

- [J]; m-masa [kg]; w-prędkość m/s. Energia

kinetyczna czynnika w dyszy rośnie kosztem jego entalpii. Największą energią kinetyczną
uzyskałby w dyszy gaz doskonały, gdyby jego entalpia podczas przepływu przez dysze

zmalała do tego stopnia żeby jego temperatura po przejściu przez dysze wynosiła 0K.
Różnice pomiędzy energią kinetyczną, którą uzyskałby czynnik po ekspansji odwracalnej
rzeczywistą energią kinetyczną którą uzyskuje po ekspansji nieodwracalnej do takiego
samego ciśnienia p

,będziemy nazywać stratą energii kinetycznej.Wskutek tarcia część

energii kinetycznej czynnika zmienia się na ciepło ogrzewające z powrotem czynnik.

II. 79 Równanie ciągłości dla cieczy.

II. 80 Równanie ciągłości dla gazów

II. 81 Równanie Bernuliego

Równanie opisujące przepływ nie zaburzony (laminarny) cieczy doskonałej wewnątrz

rury o zmiennym przekroju i położeniu:

ςgh + 0,5 ςv

+ p = const.,

gdzie: ς - gęstość cieczy, g - przyspieszenie ziemskie, h - wysokość środka przekroju nad
poziomem odniesienia, v - prędkość dla danego przekroju, p - ciśnienie w miejscu danego
przekroju.

Z równań Bernoulliego, dla prędkości cieczy v = 0 można otrzymać wzór na ciśnienie
hydrostatyczne.

II. 82 Ciśnienie statyczne, dynamiczne i całkowite.

Do rurociągu, którym przepływa gaz, wmontowano U-rurkę w ten sposób, że jeden jej koniec

jest zaopatrzony w tarczę Sera, którą wyrównuje strugę gazu drugi koniec jest zagięty pod
prąd przepływającego płyn. Na U-rurce zamontowano dwa manometry. Wskazania ich nie są
jednakowe. Manometr A wskazuje takie ciśnienia, jakie pokazywałby, gdyby się poruszał
razem z czynnikiem wzdłuż rurociągu- jest to tzw. ciśnienie statyczne p

.Natomiast

manometr B wskazuje ciśnienie większe, gdyż czynnik płynący rurociągiem wpada swoim
rozpędem do prawej gałęzi U-rurki. Ponieważ ciśnienie wskazywane przez manometr B
pochodzi nie tylko od ciśnienia statycznego płynącego gazu, lecz także od jego prędkości,
nosi ono nazwę ciśnienia całkowitego p

.Różnicę między ciśnieniem panującym w prawej

gałęzi U-rurki(wskazywanym przez manometr B) a ciśnieniem panującym w lewej gałęzi U-
rurki (wskazywanym przez manometr A) nazywamy ciśnieniem dynamicznym p

gdyż jest

ono spowodowane energią kinetyczną płynącego czynnika. Znając różnicę poziomów h
cieczy w U-rurce oraz jej ciężar właściwy ۶ można określić wartość ciśnienia dynamicznego

za pomocą wzoru

=h*۶

Ciśnienie dynamiczne-zalezy od prędkości przepływającego czynnika i jego gęstości. Można
udowodnić, że pomiędzy wielkością ciśnienia dynamicznego a prędkością i gęstością

przepływającego czynnika istnieje zależność:

ς * w

W której ς oznacza gęstość przepływającego czynnika w kg/m

, natomiast w jego prędkości

w m/s

Jak wynika z przeprowadzonego rozumowania, ciśnienie całkowite jest sumą ciśnienia
statycznego i dynamicznego.

II. 83 Lepkość płynów.

Opór jaki napotykają przesuwające się względem siebie i stykające się warstwy płyn (tarcie
wewnętrzne min. oddziaływaniem miedzy cząsteczkowym).

II. 84 Definicja lepkości i jednostki.

Lepkość można podzielić na kinematyczną [m

/s] i dynamiczną[Pa *s]

II. 85 Wpływ lepkości na przepływy.

Lepkość wpływa na spadek prędkości przepływu cieczy

0 Zasada Termodynamiki – temperatura, taka wielkość fizyczna, której równość zapewnia
równowagę termiczną ciał będących ze sobą w kontakcie.
Równowaga termiczna – jeżeli ciało A jest w równowadze termicznej z ciałem C i ciało B jest

także w równowadze z tym samym ciałem C, to oba ciała A i B są w równowadze
termicznej.

II. 86Cząsteczkowa budowa materii a stan termiczny ciał.

II. 87 Temperatura – skale.

Temp. jest określeniem zmiany stanu cieplnego ciała. W fizyce stosowane są 3 skale
termometryczne: Celsjusza, Faherenhejta i Kelvina

II.88 Zmiany właściwości ciał ze zmianą stanu termicznego – rozszerzalność.

Ze zmianą temp. ciał wszystkie ich własności ulegają zmianie. ciała stałe ciecze gazy

powiększają swoją objętość przy ogrzewaniu gazy zamknięte w stałej objętości zwiększają
ciśnienie. Ponadto zmienia się gęstość ,ściśliwość lepkość, oporność elektryczna i wiele
innych własności.

II.89 Skala Celsjusza temperatury.

Temp. wyższe od temp. wrzenia wody mają wartości większe od 100

C, natomiast temp.

niższe od punktu zerowego skali nazywamy temp. ujemnymi i oznaczamy znakiem(-) przed
liczbą wyrażającą ilość jednostki skali.

II. 90 Bezwzględna skala temperatur (K).

Punkt zerowy tej skali, zwany zerem bezwzględnym, odpowiada punktowi- 273 skali
Celsjusza, przy czym jednostki obu tych skal są sobie równe.

II. 91 I zasada termodynamiki.

I zasada-stwierdza że w zamkniętym układzie termodynamicznym, który nie zmienia swej
energii kinetycznej i potencjalnej zmiana energii wewnętrznej jest równa sumie algebraicznej
pracy oraz ciepła wymienionego z otoczeniem.

L=Q-ΔU

Z której wynika, że wykonanie pracy wymaga dostarczenia do układu ciepła z otoczenia albo
zmniejszenia energii wewnętrznej układu.

II. 92 Energia wewnętrzna ciał.

Zależy od temp., stanu skupienia, ciśnienia, objętości ciał. Ew dowolnej ilości czynnika
oznacza się symbolem U [J] Ew 1kg.czynnika oznacza się symbolem u (jest to J/kg).Ew
1kmol oznacza się symbolem Mu (j/kmol). Ew 1 kg oraz1 kmol czynnika nazywa się Ew

właściwą U=m*u U=n*Mu
Jeżeli przyjmiemy że Ew dowolnego ciała stałego lub ciekłego, nie zmieniającego swego
stanu skupienia i mającego stałe ciepło właściwe, w temperaturze O

C jest równa zeru, to

energia wewnętrzna tego ciała po pogrzaniu do temperatury t

C jest równa ilości ciepła, które

pochłonęło to ciało w czasie ogrzewania od 0

C do t

U=m*c*t

u = c*t

Mu = Mc*t

II. 93 Równoważność pracy i ciepła.

Wszystkie rodzaje pracy są całkowicie zamienialne na pracę mechaniczną a także między
sobą ponieważ przemianom tym nie towarzyszy wymiana entropii. Idealny silnik elektryczny
bez tarcia i oporu elektrycznego, zamienia całkowicie pracę prądu elektr. Na pracę mech.
Idealny generator elektr. całkowicie zamienia pracę mech. w e elektr. Ponieważ wszystkie

formy pracy są dowolnie zamienialne, więc są one sobie nawzajem równoważne
termodynamicznie

II. 94 Prawo zachowania energii.

= Δ E

+ E

; E

– E doprowadzona do układu; Δ E

– przyrost e układu; E

– e

odprowadzona z układu

II. 95 Pojemność cieplna ciał.

II. 96 Ciepło właściwe masowe i molowe

Masowe (kilogramowe) ciepło właściwe (c)– jest to ilość ciepła potrzebna do ogrzania 1 kg

ciała o 1 stopień [J/(kg*K)]. Do ogrzania m kilogramów ciała o 1 stopień potrzeba m * c
ciepła, do ogrzania zaś m kg o Δt = t

-t

stopni potrzeba ciepła Q

1-2

= m*c(t

-t

)

Przy rozpatrywaniu gazów można wyróżnić 2 rodzaje c w: o stałej objętości c

i o stałym

ciśnieniu c

. Dla gazów doskonałych i pół doskonałych istnieje zależność R = c

– c

Tak samo jest dla kilomolowego Mc

- Mc

.=R * M =8315 J/(kmol*K)

Molowe (kilomolowe) ciepło właściwe (Mc) jest to ilość ciepła potrzebna do 1 kmol ciała o 1
stopień [J/(kmol*K)]. Jeden kilomol ma masę M razy większą od 1 kg. Wynika stąd, że
kilomolowe c w jest M razy większe od kilogramowego c w. Ilość ciepła potrzebną do

ogrzania n kilomoli ciała od temp. t

do t

oblicza się Q

1-2

= m*(Mc)(t

-t

)

II. 97 Bilans cieplny.

W układzie ciał, które nie wymieniają ciepła z otoczeniem i w których nie zachodzi zamiana

ciepła na inne rodzaje energii, łączna ilość ciepła jest stała, czyli suma ilości ciepła oddanego
równa jest sumie ilości ciepła pobranego przez inne ciała tego układu. Σ Q

= Σ Q’

II. 98 II zasada termodynamiki.

a)ciepło nie może samorzutnie przejść od ciała o temp. niższej do ciała o temp. wyższej.

b)tarcie jest przemianą nieodwracalną
c)niemożliwe jest skonstruowanie perpetum mobile II rodzaju. Perpetum mobile II rodzaju

byłby to pracujący według zamkniętego obiegu silnik cieplny, który pobierał ciepło tylko z
jednego źródła o stałej temp. i w całości zamieniał to ciepło na pracę mechaniczna nie
powodują żadnych trwałych zmian w innych ciałach.

II. 99 Możliwości i ograniczenia zamiany ciepła na pracę.

Praca może być całkowicie zamieniona na ciepło, ale proces odwrotny nie jest możliwy,
ciepło nie może być całkowicie zamienione na pracę. Entropia dopływa do układu wraz z
ciepłem, ale nie opuszcza go wraz z pracą. Urządzenie zamieniające ciepło na pracę musi

koniecznie oddzielić entropię od tej części ciepła która została zamieniona na pracę. Entropia
odebrana od tej porcji ciepła nie może pozostać w urządzeniu w nie skączoność, musi
ostatecznie być od niego odebrana. Jedynym sposobem jest dostarczenie większej ilości
ciepła niż potrzeba na wytworzenie określonej pracy i oddanie nadmiaru, jako ciepła

straconego w temp. niższej niż na wlocie. Stwierdzono iż aby odprowadzić całą dostarczoną
entropię, wystarczy oddać do dolnego źródła o niższej temp. tylko określoną ilość ciepła.

II. 100 Naturalne procesy termodynamiczne w przyrodzie a II zasada.

II. 101 Entropia.

Elementarny przyrost entropii ciała jest równy ilorazowi elementarnej ilości ciepła, którą
pochłonęło to ciało, przez temperaturę bezwzględną, jaką miało to ciało w momencie

pochłaniania tego ciepła dS =

W obliczeniach przyjmuje się zwykle, że entropia ciała jest

równa zeru, gdy ciało to ma temperaturę O°C i znajduje się pod ciśnieniem 0,1 MPa 1). Jeżeli
ciało ogrzewamy od stanu, w którym entropia jego miała wartość zero do jakiegoś dowolnego
stanu 1, to entropia jego wzrasta.

II. 102 Sprawność termodynamiczna – silnik idealny.

W silniku cieplnym nie można zamieniać na pracę całego ciepła doprowadzonego do obiegu.
Na przykład w silniku spalinowym część ciepła dostarczonego podczas spalania paliwa musi

być odprowadzona do chłodnicy, a część wraz ze spalinami uchodzi do atmosfery. Udział
ciepła zamienianego na pracę decyduje o zużyciu paliwa, a więc o ekonomiczności silnika.
Do oceny tak rozumianej efektywności silnika stosuje się wielkość η , zwaną

sprawnością obiegu, wyrażoną wzorem η=

w którym: L

-praca obiegu, Q - ciepło doprowadzone do obiegu.
Ponieważ tylko część ciepła doprowadzonego może być zamieniona na pracę, sprawność η
jest zawsze mniejsza od jedności. Sprawność obiegu jest tym większa, im większa część
ciepła doprowadzonego zostanie w obiegu zamieniona na pracę.

Zgodnie z zależnością L

= Q -│Qo│, gdzie Qo oznacza ciepło odprowadzone z obiegu,

które - jak pamiętamy - ma wartość ujemną. η=

Q -│Qo│

= 1-

│Qo│

II. 103 Cykl Carnotta Termodynamiczna definicja temperatury.

To obieg odwracalny, którego górne źródło ciepła ma temperaturę T, a źródło dolne – stałą
temp. T

. Kolejne fazy pracy zespołu tłok-cylinder odpowiadają pośrednim etapom przemian,

które łączą punkty obiegu. Podczas pierwszej fazy zmniejszająca się masa tłoka oraz transport
ciepła z górnego (ciepłego) źródła powodują izotermiczne rozprężanie gazu doskonałego

zawartego w cylindrze od objętości V

do objętości V

. Podczas drugiej fazy mniejsza masa

tłoka i odizolowanie cieplne od otoczenia powodują adiabatyczne rozprężanie gazu do
największej objętości V

. Podczas trzeciej fazy zwiększająca się masa tłoka i odpływ ciepła

do dolnego (zimnego) źródła powodują izotermiczne sprężanie gazu do objętości V

. Podczas

czwartej fazy nadal zwiększająca się masa tłoka i izolacja cieplna od otoczenia powodują
adiabatyczne sprężanie gazu do najmniejszej objętości V

. Przemiany 3-4(rozprężanie

adiabatyczne) i 1-2(sprężanie adiabatyczne) - między dwiema przemianami izotermicznymi
4-1(sprężanie izotermiczne) i 2-3(rozprężanie izotermiczne) - odbywają się bez wymiany

ciepła, a ponieważ są ponadto odwracalne, pozostają przemianami adiabatycznymi -

izentropowymi, dla których jest spełniony warunek: dS =

=0 Jest to więc przemiana przy

stałej entropii. Sprawność obiegu Carnota η= 1-

│Qo│

= 1-. η=

- S

)

T(S

- S

)

= 1-

II. 104 III zasada termodynamiki.

Układ w stanie równowagi, w temperaturze zera bezwzględnego T = 0K znajduje się w stanie
maksymalnego uporządkowania, a jego entropia wynosi zero. Jeżeli temperatura ciała dąży do
zera bezwzględnego, to jego ciepło właściwe i współczynnik rozszerzalności cieplnej też dążą

do zera. Z trzeciej zasady termodynamiki wynika, że nie można osiągnąć temperatury zera
bezwzględnego

II. 105 Ograniczenia przekazywania energii w niskich temperaturach.

II. 106 Niemożliwość osiągnięcie zera w bezwzględnej skali temperatur.

II. 109 Zero w bezwzględnej skali temperatur a cząsteczkowa budowa materii.

Najmniejsza możliwa temperatura równa -273,15°C = 0 K. Zero bezwzględne odpowiada
stanowi materii o najmniejszej możliwej energii.

II. 110 Właściwości gazu doskonałego.

Gaz doskonały ma 4 następujące własności:
1. Stosuje się do prawa Boyle'a i Mariotte'a. gdy t =const to pv = const p

= p

2. Stosuje się do prawa Gay-Lussaca. gdy p =const to

= const

3. Stosuje się do prawa A vogadra. Jeżeli w 3 różnych zbiornikach są różne gazy a p,v i t jest

identyczne to w każdym z tych zbiorników znajduje się taka sama ilość cząsteczek gazu.
4. Ma stałe ciepło właściwe.
Gaz półdoskonały stosuje się do wymienionych trzech praw, ale jego ciepło właściwe nie jest
stałe i zależy od temperatury (w temperaturach wyższych jest większe niż w temperaturach

niższych).

II. 111 Kinetyczna teoria gazu doskonałego.

II. 112 Model gazu doskonałego.

II. 113 Wymiana pędu i energii cząsteczek gazu ze ścianką naczynia.

II. 114 Ciśnienie gazu.

Jeżeli do zbiornika zawierającego określony gaz zostanie wprowadzony inny gaz, to będą one
tworzyć jednolitą mieszaninę. Wykrycie zależności, w jakiej pozostaje ciśnienie mieszaniny

gazów od ciśnienia jej składników, zawdzięczamy Daltonowi. Prawo Daltona stwierdza, że
ciśnienie p wywierane w zbiorniku przez mieszaninę gazów równa się sumie ciśnień p

, p

...

, jakie w tymże zbiorniku wywierałby każdy ze składników mieszaniny, gdyby sam tylko

wypełniał zbiornik p = p

+ p

+ . . . + p

Jeżeli na przykład do pustego zbiornika, mającego pojemność 10 litrów zostanie
wprowadzony 1 litr tlenu, odmierzony pod. ciśnieniem 1 atmosfery, wywiera on tam zgodnie
z prawem Boyle-Mariotte'a ciśnienie równe 0,1 at; jeżeli następnie do tegoż zbiornika
wpuszczony będzie 1 litr azotu, odmierzony również pod ciśnieniem 1 at, to połączony ze

zbiornikiem manometr wykaże, że utworzona mieszanina wywiera ciśnienie równe 0,2 at.
Ciśnienie mieszaniny byłoby takie samo, gdybyśmy naprzód wpuścili azot, a potem tlen.

II. 115 Równanie stanu gazu doskonałego.

pv=RT; ponieważ vm=V to pV=mRT

II. 116 Temperatura jako miara energii kinetycznej cząsteczek gazu.

Dwa zaizolowane zbiorniki połączono ze sobą rurką, na której umieszczono zawór. W
zborniku A znajdował się gaz o temperaturze t

, pod ciśnieniem P

W zbiorniku B była

natomiast zupełna próżnia. Po otwarciu zaworu ciśnienia i temperatury w obu zbiornikach po

chwili się wyrównały. Okazało się, że ciśnienie P

panujące w obu zbornikach jest wtedy

mniejsze od ciśnienia P

panującego przedtem w zbiorniku A. Gdy obydwa zbiorniki

otoczymy wspólną osłoną kontrolną i rozpatrzymy tak wyodrębniony układ, to przekonamy

się, że energia wewnętrzna gazu nie uległa zmianie, gdyż żadnej energii do niego nie

doprowadzono ani też od niego nie odprowadzono. Widzimy więc, że pomimo zmiany

ciśnienia i objętości nie zmieniła się energia wewnętrzna czynnika, chociaż zmieniła się jego
egzergia.

Gdy znajdujący się przed doświadczeniem w zbiorniku A czynnik miał takie parametry, że

można go było traktować jak gaz doskonały lub półdoskonały, to wspólna temperatura t2,

która ustaliła się w obu zbiornikach po otwarciu zaworu, jest równa temperaturze t l' która

panowała w zbiorniku A przed otwarciem zaworu. Nasuwa się przeto przypuszczenie, że do

zmiany energii wewnętrznej tego gazu konieczna jest zmiana jego temperatury.

Doświadczenia takie powtórzono wiele razy i stwierdzono ostatecznie, że energia wewnętrzna
gazu doskonałego i półdoskonałego zależy tylko od jego temperatury, a nie zależy od jego

ciśnienia i objętości.

Wzór służący do obliczania energii wewnętrznej gazu doskonałego i półdoskonałego

zawierać więc musi symbol T lub t, a nie zawiera symboli P, V, v.

Jeżeli przyjmiemy, że energia wewnętrzna gazu doskonałego w temperaturze O K wynosi
zero, to energia wewnętrzna tego gazu o dowolnej temperaturze T K równa jest ilości ciepła,

które musimy doprowadzić, aby ogrzać ten gaz od O K do T K. Słuszne to jednak jest tylko
wtedy, gdy doprowadzane ciepło jest zużywane tylko do zwiększenia energii wewnętrznej
czynnika (a nie np. częściowo do wykonywania pracy). Dlatego ogrzewanie to musi odbywać
się w stałej objętości. Do obliczania więc energii wewnętrznej gazów doskonałych służą
wzory

U = m*c

*T = n*(Mc

)*T

II. 117 Zasada ekwipartycji energii.

Zasada równego podziału energii na poszczególne stopnie swobody w układzie, który jest w

stanie termodynamicznej równowagi.

II. 118 Właściwe ciepło molowe gazu a budowa cząsteczek.

II. 120 Przemiana izotermiczna

Przemianę izotermiczną gazu doskonałego i półdoskonałego w układzie pracy wyraża

odcinek hiperboli, której asymptotami są osie układu. L

1-2

= p

Wstawiając do wzoru

ważną dla izotermy zależność p

= p

otrzymamy wzór L

= L

1-2

Wzór potrzebny do obliczania ilości ciepła, którą musimy doprowadzić do gazu

doskonałego lub półdoskonałego podczas przemiany izotermicznej, wyprowadzimy
posługując się pierwszą postacią równania pierwszej zasady termodynamiki ΔQ

1-2

= ΔU + L

1-2

w którym podstawiamy ΔU=0 gdyż T

= T

1-2

= L

1-2

Ilość ciepła doprowadzonego do gazu podczas przemiany izotermicznej jest więc równa pracy
bezwzględnej wykonanej przez ten gaz- Podkreślić należy, że zależność ta jest słuszna tylko
dla przemiany izotermicznej gazu doskonałego i półdoskonałego, gdyż tylko podczas takiej
przemiany energia wewnętrzna gazu doskonałego i półdoskonałego zachowuje wartość stałą
(U

= U

)

II. 121 Przemiana izochoryczna.

Izochorą nazywamy przemianę, podczas której nie zmienia się objętość czynnika (V = const).

Przemianę tę w układzie pracy przedstawia odcinek linii prostej równoległej do osi p

Zależność pomiędzy temperaturą a ciśnieniem gazu podczas tej przemiany wyprowadzimy

dzieląc przez siebie stronami dwa równania stanu gazu. Pierwsze z tych równań odnosi się do

stanu początkowego czynnika, drugie zaś do jego stanu końcowego. W równaniach tych

wskaźniki 1 i 2 są umieszczone tylko przy symbolach ciśnienia i temperatury, gdyż objętość,

stała gazowa i masa czynnika nie et zmieniają się podczas przemiany izochorycznej.

V = m R T

Wzór ten przedstawia nam prawo Charlesa: ciśnienie bezwzględne gazu doskonałego i
półdoskonałego podczas przemiany izochorycznej zmienia się wprost proporcjonalnie do

temperatury wyrażonej w kalwinach).
Rzutując odcinek przedstawiający tę przemianę na oś V przekonać się można, że praca
bezwzględna tej przemiany jest równa zeru L

1-2

= 0

Z równania wynika zatem, że ciepło doprowadzone do czynnika podczas tej przemiany

zostaje w całości zużyte do powiększenia jego energii wewnętrznej Q

1-2

= ΔU = U

-U

W przypadku gazów doskonałych można też użyć wzoru Q

1-2

= m* c

-T

) = n* Mc

-T

)

Rzutując odcinek przedstawiający tę przemianę na oś p łatwo możemy się przekonać, że
praca techniczna przemiany izochorycznej wynosi L

= V * (p

– p

)

II. 121 Przemiana izobaryczna.

Jest to przemiana, podczas której ciśnienie czynnika nie zmienia się p= const. W układzie
pracy (pv) przemianę tą przedstawia odcinek linii prostej równoległej do osi V.

Prawa Gay-Lussaca.

Praca bezwzględna tej przemiany przedstawiona jest na wykresie polem prostokąta o

wysokości p i podstawie (V

-V

) i wynosi L

1-2

= p*( V

-V

)

Rzutując linię przedstawiającą tę przemianę na oś p widzimy, że praca techniczna tej
przemiany jest równa zeru L

Ilość ciepła, którą musimy doprowadzić do gazu podczas tej przemiany, wynosi Q

1-2

m*c

-T

) = n*Mc

-T

)

Do obliczenia ilości ciepła, które musimy doprowadzić do czynnika podczas przemiany
izobarycznej, można wykorzystać też drugą postać pierwszej zasady termodynamiki, w której
zgodnie ze wzorem wstawiamy L

1-2

= I

-I

II. 122 Równanie Mayera.

Dla gazu doskonałego związek pomiędzy ciepłem właściwym przemiany izochorycznej C

(przemiana izochoryczna) a ciepłem właściwym przemiany izobarycznej C

(przemiana

izobaryczna).

II. 123 Przemiana adiabatyczna.



Adiabata jest to przemiana, podczas której nie doprowadzamy ani też nie odprowadzamy
ciepła do czynnika: Q

l-2

= 0. Zależność pomiędzy ciśnieniem a objętością czynnika podczas

odwracalnej przemiany adiabatycznej gazu doskonałego wyraża równanie

= const κ =

(Mc

)

(Mc

)

z wzoru wynika

= (

)

Przemianę adiabatyczną w układzie pracy przedstawia odcinek linii krzywej, bardziej stromej
od izotermy. Asymptotami tej krzywej są również osie układu.

Zależności

Pracę bezwzględną przemiany adiabatycznej można obliczyć posługując się równaniem ΔQ

= ΔU + L

1-2

w którym podstawiamy Q

1-2

=0, a ΔU = U

-U

równanie to po przekształceniu

przyjmuje wtedy postać L

1-2

= U

– U

U = m* c

* T...

Widzimy więc, że podczas adiabatycznego rozprężania czynnik wykonuje pracę bezwzględną
jedynie kosztem swojej energii wewnętrznej.
L

= κ * L

1-2

II. 125 Zmiany stanu skupienia materii.

Temperaturę wrzenia nazywamy również temperaturą nasycenia i oznaczamy symbolem t

Ciecz, która osiągnęła już temperaturę wrzenia, ale jeszcze nie zaczęła wrzeć, będziemy

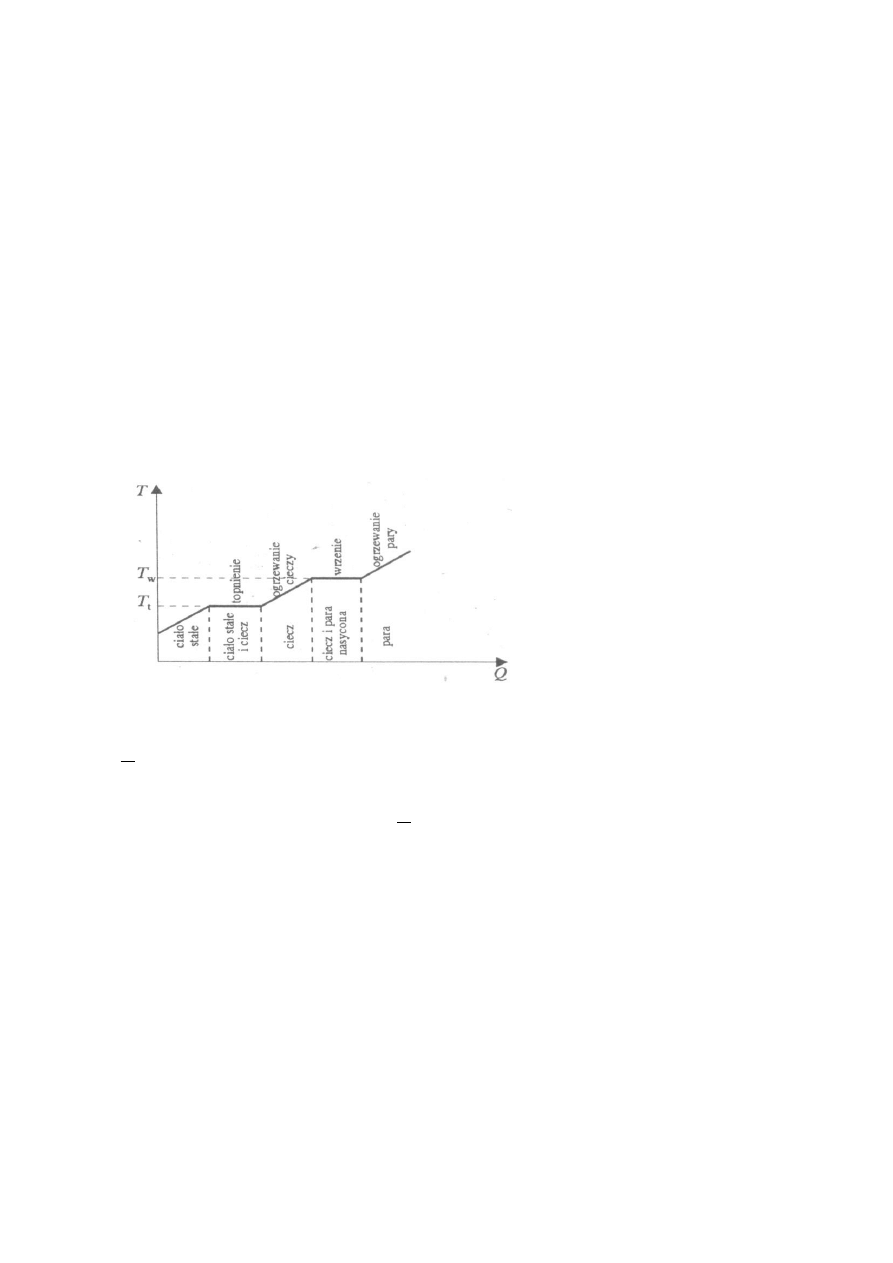
nazywać cieczą w punkcie pęcherzyków (lub cieczą nasyconą). Mieszaninę cieczy i pary
będziemy nazywać nasyconą parą mokrą lub krótko parą mokrą. Parę, która ma jeszcze

temperaturę nasycenia, ale nie zawiera już kropelek cieczy - parą nasyconą suchą, parę zaś o
temperaturze wyższej od temperatury nasycenia - parą przegrzaną.
Gdy uzyskaną parę przegrzaną będziemy pod tym samym ciśnieniem ochładzać, to
przekonamy się, że skraplanie, czyli kondensacja, będzie odbywać się dokładnie w tej
samej temperaturze), w której odbywało się wrzenie, natomiast krzepnięcie, czyli
zamarzanie, w tej temperaturze, w której odbywał się proces topnienia. Ilość ciepła, która
musi być odprowadzona podczas procesu skraplania jest dokładnie równa ciepłu
parowania. Ilość zaś ciepła, która musi być odprowadzona w procesie krzepnięcia jest

dokładnie równa ciepłu topnienia. Zjawisko sublimacji polega na bezpośrednim
przechodzeniu ciała stałego w gaz (w parę). Zjawisko sublimacji wykorzystuje się w róż-
nych celach np. w wagonach "na suchy lód", które służą do przewożenia produktów
żywnościowych. W wagonach tych umieszcza się bryły dwutlenku węgla. Bryły te nie

topią się, lecz sublimują. Ponieważ sublimujący dwutlenek węgla pobiera wielkie ilości
ciepła, temperatura w wagonie się obniża. Używanie "suchego lodu" jest praktyczniejsze
od używania zwykłego lodu, gdyż topniejący zwykły lód zawilgoci wagon i przewożone
w nim produkty. Natomiast dwutlenek węgla może być cieczą tylko wtedy, gdy znajduje

się pod ciśnieniem wyższym niż 0,518 MPa. Przy niskim ciśnieniu cząstkowym pary
wodnej w powietrzu mamy do czynienia z sublimacją

II. 126 Wykres T(Q).

Ciepło przemiany.

Ilość ciepła, którą musimy doprowadzić, aby 1 kg ciała stałego o temperaturze topnienia
zamienić całkowicie na ciecz (o tej samej temperaturze), nazywamy ciepłem topnienia. q

[J/kg] Natomiast ilość ciepła, jaką musimy doprowadzić, aby 1 kg cieczy w

punkcie pęcherzyków zamienić izobarycznie w parę nasyconą suchą ciepłem parowania

lub entalpią parowania (symbol r). Q

[J/kg]

Parametry krytyczne gazu. W miarę wzrostu ciśnienia maleje wartość ciepła parowania,
aż wreszcie przy ciśnieniu 22,129 MPa przyjmuje ono wartość zero. Pod ciśnieniami
wyższymi niż 22,129 MPa nie mamy już do czynienia ze zjawiskiem wrzenia. Gdy
weźmiemy wodę (ciecz) i będziemy ogrzewać ją izobarycznie pod ciśnieniem wyższym

od 22,129 MPa od temperatury O°C do temperatury 1000°C, to w temperaturach niskich
czynnik będzie miał własności zbliżone do własności cieczy, a w temperaturach wysokich
własności zbliżone do własności pary przegrzanej (gazu). Ale ta zmiana własności nastę-
pować będzie powoli w miarę wzrostu temperatury bez zjawiska wrzenia. Z tego powodu
o H

0 pod ciśnieniem wyższym od 22,129 MPa mówimy, że znajduje się w stanie

ciągłości gazowo-ciekłej. Krzywa parowania na wykresie (p, t) I kończy się więc przy
ciśnieniu 22,129 MPa w punkcie K zwanym punktem! krytycznym. Temperaturę
nasycenia odpowiadającą punktowi krytycznemu nazywać będziemy temperaturą
krytyczną i oznaczać symbolem t

ciśnienie zaś odpowiadające punktowi krytycznemu

nazywać będziemy ciśnieniem krytycznym i oznaczać symbolem Pk. Parametry krytyczne
dla H

0 mają wartości p

= 22,129 Mpa, t

= 374,15

C Można by sądzić, że im wyższe

ciśnienie w kotle, tym tańsza powinna być para przegrzana o określonej entalpii, gdyż
tym mniej ciepła wymaga proces wrzenia i tym wyższa jest temperatura, w której zaczyna
się proces przegrzewania pary. Okazuje się jednak, że tak nie jest, ponieważ zgodnie z

zasadą zachowania energii izobaryczne zwiększenie entalpii czynnika wymaga określonej
ilości ciepła bez względu na ciśnienie, pod którym proces ten się odbywa. Należy pod-

kreślić, że przy wysokim ciśnieniu wodę musimy podgrzać do dość wysokiej temperatury,
by zaczęła wrzeć, a w wysokiej temperaturze woda (ciecz) ma duże ciepło właściwe. Im
więc wyższe ciśnienie, tym więcej ciepła musi być doprowadzone do procesu
podgrzewania cieczy. Suma zaś ciepła koniecznego do izobarycznego podgrzewania
wody, jej odparowania i przegrzania nie zależy od ciśnienia, mimo że każda z tych trzech
przemian przy różnych ciśnieniach wymaga różnych ilości ciepła. Suma ta zależy tylko
od entalpii początkowej i końcowej czynnika i to nawet wtedy, gdy proces odbywa się
przy ciśnieniu ponad krytycznym.

Wykres fazowy V(T), punkt potrójny dla wody. Jeżeli dana substancja może
występować w trzech stanach skupienia, to każdej parze faz można wykreślić we
współrzędnych p, T krzywe równowagi: między ciałem stałym a cieczą, między ciałem
stałym a parą, między cieczą a parą (współrzędne każdego punktu takiej krzywej opisują

warunki równowagi fazowej). Krzywe te przecinają się w punkcie P zwanym punktem
potrójnym, którego współrzędne wyznaczają warunki umożliwiające występowanie w
stanie równowagi wszystkich trzech faz. Parametry tego punktu dla H

O wynoszą P

611 Mpa; t

= 0,0098 ≈ 1

p - punkt potrójny; k – punkt krytyczny; T

–

temperatura krytyczna, powyżej której ciało może istnieć tylko w stanie gazowym (bez
względu na ciśnienie); p

– ciśnienie krytyczne.

Elektryzowanie ciał. Doświadczenie. Pałeczki wykonane z ebonitu i szkła elektryzujemy

przez potarcie futrem (pałeczki ebonitowej) i jedwabiem (pałeczki szklanej), a następnie
zawieszamy na jedwabnych nitkach, zakończonych metalowymi strzemiączkami i badamy ich
wzajemne oddziaływanie na siebie. Stwierdzamy, że dwie naelektryzowane pałeczki
ebonitowe lub dwie szklane odpychają się wzajemnie, natomiast pałeczka szklana z

ebonitową - przyciągają się. Badając w ten sposób własności innych ciał można stwierdzić, że
elektryzują się one tak Jak ebonit potarty futrem, to znaczy odpychają naelektryzowaną
pałeczkę ebonitową, albo tak jak szkło potarte jedwabiem, czyli odpychają naelektryzowaną

pałeczkę szklaną. Ciała posiadające własności takie, jak szkło potarte jedwabiem, nazywamy
dodatnio naelektryzowanymi, natomiast takie, jak ebonit potarty futrem- naelektryzowanymi
ujemnie. Omówione wyżej doświadczenie wykazuje, że ciała naelektryzowane jednoimienne
( obydwa dodatnio lub obydwa ujemnie) - odpychają się, a naładowane różnoimiennie (jedno
dodatnio a drugie ujemnie) - przyciągają się.
Elektron. Cząstka elementarna ładunku elektrycznym równym q = -1,6021917(70)10

-19

masie m = 511,0041(16)keV/c

= 9,1091

⋅ 10

-31

kg. Elektron jest tą cząstką elementarną

materii która najczęściej przemieszcza się pod wpływem oddziaływań, lub reakcji
chemicznych.
Ładunek elektryczny. Duże Ciała zawierają taką samą liczbę elektronów i protonów, duże
przyciągające i odpychające siły elektrostatyczne znoszą się wzajemnie, a pozostaje jedynie
słaba siła grawitacyjna. Źródłem siły grawitacyjnej jest masa grawitacyjna lub ładunek

grawitacyjny podobnie źródło siły elektrostat. jest nazywane ład elektrycznym. Masa czy
ładunek cząstki, są właściwie atrybutami matematycznymi które mówią nam jak siła
grawitacyjna czy siła elektrostat. działa na daną cząstkę

Elektryzowanie ciał jako efekt wymiany elektronów. Nadmiar elektronów powoduje naelektryzowanie ciał
ładunkiem ujemnym, a ich niedobór ładunkiem dodatnim

Ładunek elementarny. Elektron jest tą cząstką elementarną
Prąd elektryczny.

PRĄD ELEKTRYCZNY JEST STRUMIENIEM PRZEPŁYWAJĄCYCH

ŁADUNKÓW ELEKTRYCZNYCH ELEKTRONÓW LUB JONÓW,

Amper jest natężeniem prądu, który przepływa w dwu równoległych umieszczonych

w próżni w odległości 1m od siebie przewodnikach, jeżeli na każdy metr długości
przewodnika działa siła F = 2 .10 -7N
Natężenie prądu a ładunek elektryczny (C) Możemy je zmierzyć poprzez pomiar sił

oddziaływania między przewodnikami w których ten prąd przepływa. Jednostką jest

Amper. Oddziaływania elektryczne. Między ładunkami elektrycznymi występują
oddziaływania, tzn. działają siły: - odpychające między ładunkami równoimiennymi - i

przyciągające między ładunkami różnoimiennymi a ich wartość określa prawo

Coulomba W próżni:







Oddziaływanie ciał naelektryzowanych. Miarą naelektryzowania ciała jest zgromadzony na
nim ładunek elektryczny Q , który jest iloczynem natężenia prądu z jakim przepływały

ładunki i czasu jego przepływu Q = I t Jednostką ładunku jest Coulomb [ C ] C = A

Prawo Coulomba. Siła F wzajemnego oddziaływania(przyciągania lub odpychania) dwóch

ładunków elektrycznych q1 i q2,znajdujących się od siebie w odległości r jest wprost
proporcjonalna do wielkości tych ładunków, a odwrotnie proporcjonalna do kwadratu
odległości miedzy nimi. F =k

*q1*q2/r

Natężenie pola elektrostatycznego. Jeżeli w pewnym punkcie pola elektrostatycznego,
wytworzonego przez ładunek Q, umieścimy niewielki ładunek próbny q, to znajdzie się on

pod działaniem siły F =

Q q

ε r

gdzie r jest odległością obydwu ładunków. Wartość siły P jest

różna w różnych punktach pola, a jej stosunek do wielkości ładunku próbnego jest dla
każdego punktu wielkością charakterystyczną i stanowi miarę natężenia pola

elektrostatycznego K w tym punkcie K =

Miarą natężenia pola elektrostatycznego w

danym punkcie pola jest stosunek wielkości siły elektrostatycznej P dzialajqcej na
umieszczony w tym punkcie ladunek elektryczny q, do wielkości tego ładunku.
Napięcie. (V) Pole elektrostatyczne ładunku punktowego i kuli naelektryzowanej
Dielektrykami nazywamy materiały, które nie przewodzą ładunków elektrycznych.
W naelektryzowanej kuli dielektrycznej (o promieniu R) ładunek rozkłada się równomiernie

w całej objętości kuli Pole elektryczne na zewnątrz kuli (dla r>R) jest takie jakie wytworzyłby
całkowity ładunek zawarty w kuli gdyby umieszczony był w jej centrum. E~1/r2 Pole
elektryczne wewnątrz kuli (dla r<R) jest takie jakie wytworzyłby ładunek zawarty w kuli o

promieniu r gdyby umieszczony był w jej centrum E~r
Przewodnikami nazywamy materiały, które przewodzą ładunki elektryczne bez przeszkód.
W naelektryzowanej kuli przewodzącej (o promieniu R) ładunek rozkłada się równomiernie
na powierzchni kuli na skutek działania sił odpychających Pole elektryczne na zewnątrz kuli
(dla r>R) jest takie jakie wytworzyłby całkowity ładunek zawarty na powierzchni kuli gdyby
umieszczony był w jej centrum E~1/r2. Pole elektryczne wewnątrz kuli (dla r<R) jest takie
jakie wytworzyłby ładunek zawarty w kuli o promieniu r, a jest on równy zeru E=0

Pojemność elektryczna ciał (F). Jeżeli na jakim ciele zgromadzimy ładunek elektryczny to
potencjał na powierzchni tego ciała będzie zależał od wartości tego ładunku oraz właściwości

tego ciała nazywanej pojemnością elektryczną

 



Pojemnością elektryczną nazywamy stosunek ładunku elektrycznego zgromadzonego na ciele

do wytworzonego prze niego potencjału Jednostką pojemności el. jest Farad jest to pojemność
ciała na którym ładunek jednego 1C wytwarza potencjał 1V
Energia ciała naelektryzowanego.Doładowanie ciała ładunkiem dq wymaga wykonania

pracy dL=U

dq Jeżeli ładowanie wykonano od q = 0 do q = Q to praca przy tym wykonana,

zamieniona na energię naelektryzowanego ciała jest równa:

























Kondensator płaski. Pojemność kondensatora płaskiego o powierzchni płytek S oddalonych

równa :



















Energia pola elektrycznego Jeżeli naelektryzowanym ciałem jest kondensator płaski to jego
energię możemy przypisać polu znajdującemu się między jego okładkami









Stąd gęstość energii pola między okładkami kondensatora jest równa:









Pole elektryczne zawiera w sobie energię o gęstości proporcjonalnej do kwadratu natężenia

pola:











Prawa Ohma dla prądów. Natężenie prądu płynącego w przewodniku jest wprost propor-
cjonalne do napięcia przyłożonego do końców przewodnika Zależy ono od właściwości
przewo-dnika nazywanej oporem . Opór przewodnika zależy od jego długości (l) i przekroju

(S), oraz właściwości materiału - oporu właściwego

Natężenie prądu





Opór elektryczny. Jednostką oporu nazywanego też rezystancją jest Om Jest to opór
przewodnika w którym przy napięciu 1V między jego końcami przepływa prąd o natężeniu
1A
Opór właściwy.
czyli opór rośnie z wzrostem temperatury Dla niektórych półprzewodników takich jak

Dla półprzewodników , oraz elektrolitów (wodnych roztworów zasad, kwasów i soli) gdzie

temperatury













Prawa zachowania ładunku a I prawo Kirchoffa. Suma natężeń prądów wpływających do

węzła obwodu jest równa sumie natężeń wypływających.







Prawa zachowania energii a II prawo Kirchoffa. Suma spadków napięć w każdej pętli
obwodu elek-trycznego jest równa sumie sił elektromotorycznych włączonych w tej pętli







)

(













Pole indukcji magnetycznej. Polem magnetycznym nazywamy przestrzeń w której na
ładunki elektryczne działa siła zależna od ich prędkości nazywana siłą Lorentza.

B nazywamy polem indukcji magnetycznej,

Wektor indukcji magnetycznej. Indukcja magnetyczna jest to stosunek siły działającej na
poruszający się ładunek elektryczny do iloczynu wartości tego ładunku i jego prędkości

Jednostką indukcji magnetycznej jest Tesla - T

 











Prawo Biotta – Savarta. Każdy element długości przewodnika wytwarza pole magnetyczne

o natężeniu:











lub indukcji magnetycznej













Pole magnetyczne wokół przewodnika prostego. Prąd płynący w przewodniku wytwarza
wokół przewodnika pole magnetyczne. Jego natężenie wokół przewodnika prostego można

określić z prawa Biota – Savarta jako całkę wzdłuż przewodnika nieskończenie

długiego

















sin













Prawo Ampera. Obliczmy całkę liniową po okręgu otaczającym przewodnik











Podobnie dla dowolnej linii









Indukcja elektromagnetyczna. Jeżeli przez powierzchnię objętą zamkniętym obwodem
elektryc-nym przenika zmieniający się w czasie strumień indukcji magnetycznej to w
obwodzie tym generuje się siła elektromotoryczna równa szybkości zmian tego strumienia

(prawo indukcji Faradaya)









Prawa Maxwella.









































































Widmo fal elektromagnetycznych Kolejnym wartościom wielokrotności długości fal w
różnicy dróg optycznych fal ugiętych na sąsiednich szczelinach siatki odpowiadają kolejne

rzędy ugięcia co tworzy widma kolejnych rzędów
Światło jako fala elektromagnetyczna. Optyka geometryczna wynika z praw ruchu
falowego dla a>>λ dyfrakcja fal świetlnych, interferencja fal, widma promieniowania,
prędkość światła.

Falowa natura światła. Światło jest falą elektromagnetyczną ale skwantowaną czyli
emitowaną w porcjach nazywanych fotonami o energii:E

= hν Fotonom można przypisać

masę: m

= E

/ c

oraz pęd: p

=h/λ co pozwala światło interpretować jako zbiór cząsteczek

(korpuskuł) Światło tak jak każde zjawisko fizyczne odkrywa nam swoją naturę zależnie od

metody jego badania. W zjawisku możemy zaobserwować tylko to na co pozwala nam
sposób jego obserwacji
Zakres widmowy światła widzialnego. Zakres fal elektromagnetycznych o długościach fal
od 0,4 λm do 0,7μm jest rejestrowany przez człowieka przy pomocy oka. Jego czułość jest

maksymalna dla: λ=0,55μm, a różne długości fal odbierane są jako różne barwy (barwy proste
światła widzialnego)
Promieniowanie ciała doskonale czarnego. Z prawa Plancka wynikają wszystkie prawa
promieniowania ciała doskonale czarnego
Rozkład widmowy promieniowania ciał stałych. Ciała stałe emitują widmo
ciągłe które zależne jest od temperatury ciała. Klasyczna elektromagnetyczna teoria
światła nie jest jednak w stanie wytłumaczyć kształtu ich widma
Prawa Wiena i Stefana Boltzmana. Położenie maksimum widma promieniowania

zmienia się z temperaturą wg prawa Viena:

const





max



Całkowita moc

promieniowania zmienia się z temperaturą wg prawa Stefana - Boltzmana:

)

(

cał











Prawo Plancka. Elektrony wypromieniowują energię tylko skończonymi porcjami

kwantami o wartości E = h

kwantowa natura energii oscylatorów h = 6,626

-34

s Wówczas widmo promieniowania zbioru elektronów w temperaturze T ma

postać:

)

(















Kwantowa natura światła. Klasyczna teoria promieniowania fali
elektromagnetycznej przez zbiór dipoli którymi są drgające elektrony na powierzchni
ciała doskonale czarnego sugeruje silny wzrost energii wypromieniowanej z wzrostem
częstotliwości. Poprawny przebieg dE(λ)/dλ można otrzymać gdy założy się, że

energia ta może być wypromieniowywana tylko małymi skończonymi porcjami -
kwantami. (postulat Plancka)
Zjawisko fotoelektryczne. Układ katody metalowej i anody umieszczone w próżni
mogą przewodzić prąd elektryczny gdy katoda zostanie oświetlona silnym
strumieniem światła.
Natężenie fotoprądu i energia fotoelektronów. Natężenie prądu
fotoelektrycznego zależy od oświetlenia, liczba wybitych fotoelektronów zależy od
natężenia światła Zjawisko fotoelektryczne zachodzi gdy długość fali światła jest
krótsza od pewnej wartości granicznej (długofalowa granica zjawiska
fotoelektrycznego) Aby zjawisko fotoelektryczne zaistniało częstotliwość padającego
promieniowania musi być wystarczająco duża. Energia wybitych foto-elektronów jest
zależna od częstotliwości padającego promieniowania, musi ona być wyższa od
częstotliwości granicznej. Nie ma żadnego opóźnienia między początkiem oświetlania
i zaistnieniem fotoprądu.
Kwantowe założenie Einsteina. Zjawisko fotoelektryczne zostało wytłumaczone
przez Einsteina w oparciu o założenie kwanto-wej natury światła. Swiatło może
przekazywać energię skończonymi porcjami - kwantami o wartości ΔE=hν Prawo
zachowania energii w zjawisku fotoelektrycznym ma postać: (P - praca wyjścia

elektr.)







Fotony. (E

, m

)Światło jest falą elektromagnetyczną emitowa-ną w porcjach

nazywanych fotonami o energii: E

= hν w związku z prawem równoważności masy i

energii można im przypisać masę (relatywistyczną) m

= E

/ c

fotonowi można także

przypisać pęd (relatywistyczny).
Oscylatorowy model atomu Thomsona. Atom jest jednorodną kroplą materii

dodatniej (d≈10

-10

m) Elektrony oscylujące wokół położeń równowagi rozmieszczone

są w atomie w różnych miejscach i jak dipole elektryczne oddziaływają z falą
elektromagnetyczną (światłem).
Doświadczenia Rutheforda i jego model. Atom zbudowany jest z jądra w

którym skupiona jest prawie cała jego masa i cały ładunek dodatni rj=10

-14m

Ujemne elektrony krążą wokół jądra po orbitach kołowych ro=10

-10m

Postulaty Bohra i jego model atomu wodoru. I Elektron krążąc po orbicie
stacjonarnej nie promieniuje energii II Elektron promieniuje energię lub ją pochłania
gdy przeskakuje z orbity na orbitę
Liczby kwantowe. n = 1, 2, 3, - numer orbity l = 0 (s),1(p),2(d),3(f),.(n-1)-
orbitalny moment pędu m= (-l+1), ., -1, 0 , 1,.(l-1),-rzut o.m.p na kierunek z s = -
1/2, 1/2 - spinowy moment pędu j= l+s = -1/2, 1/2, 3/2, 5/2, sumaryczny moment
pędu ns

- Symboliczny zapis stanu elektronowego k - krotność stanu (l. elektronów)

Wyszukiwarka

Podobne podstrony:
PYTANIA Z EGZAMINU Z FIZYKI
pytania z egzaminu i poprawne odpowiedzi
Pytania egzaminacyjne z fizyki sem II, Studia, Sem 2, SEMESTR II, SEMESTR I, fizyka, haksy, Fiza
Pytania egzaminacyjne MR odpowiedzi, Ratownictwo WOPR + Nurkowanie, Egzamin Karta umiejetności Pytan
opracowane pytania z egzaminu z fizyki u Cieślaka styczeń
Poznaj pytania egzaminacyjne z zakresu oceny ochrony cieplnej z odpowiedziami
PYTANIA EGZAMINACYJNE i Odpowiedzi
Pytania z egzaminu z odpowiedziami
Odpowiedzi na pytania z egzaminu 2
odpowiedzi na pytania egzamin
Odpowiedzi na pytania egzaminacyjne z Technologii Informacyjnych
Wstęp do religioznawstwa pytania egzaminacyjne i odpowiedzi
pytania egzaminacyjne na egzaminatora prawa jazdy, ODPOWIEDZI- obsuga D, ODPOWIEDZI - TECHNIKA KIERO
pytania egzaminacyjne na egzaminatora prawa jazdy, ODPOWIEDZI KATEGORIA B, ODPOWIEDZI KATEGORIA &b
pytania egzaminacyjne na egzaminatora prawa jazdy, ODPOWIEDZI- obsuga C, ODPOWIEDZI - TECHNIKA KIERO
pytania egzaminacyjne na egzaminatora prawa jazdy, ODPOWIEDZI- obsuga C, ODPOWIEDZI - TECHNIKA KIERO
Pytania do egzaminu z fizyki sem.1 teoria
prawoznawstwo, Pytania egzaminacyjne z odpowiedziami., 1

więcej podobnych podstron