549

Górnictwo i Geoin

Īynieria • Rok 35 • Zeszyt 2 • 2011

Joanna Stró

Īyk*

ZASTOSOWANIE RÓWNAē WSKAħNIKA ĝCIĝLIWOĝCI C

C

DO OCENY ĝCIĝLIWOĝCI IàÓW SERII POZNAēSKIEJ

1. Wst

Ċp

ĝciĞliwoĞü gruntów, obok ich wytrzymaáoĞci, jest jedną z najistotniejszych cech podáoĪa

branych pod uwag

Ċ na etapie projektowania konstrukcji inĪynierskich, posadawianych na pod-

áoĪu gruntowym. ĝciĞliwoĞü charakteryzuje zmianĊ objĊtoĞci gruntu wobec zwiĊkszającego
si

Ċ obciąĪenia. Dla celów inĪynierskich najczĊĞciej oznaczana jest w laboratorium, w stanie

jednoosiowego odkszta

ácenia, w teĞcie edometrycznym. Na jego podstawie wyznaczyü moĪ-

na podstawowe parametry charakteryzuj

ące ĞciĞliwoĞü: edometryczny moduá ĞciĞliwoĞci E

oed

,

wska

Ĩnik ĞciĞliwoĞci i odprĊĪenia C

c

i C

s

oraz napr

ĊĪenie prekonsolidacji

v’

p

[9].

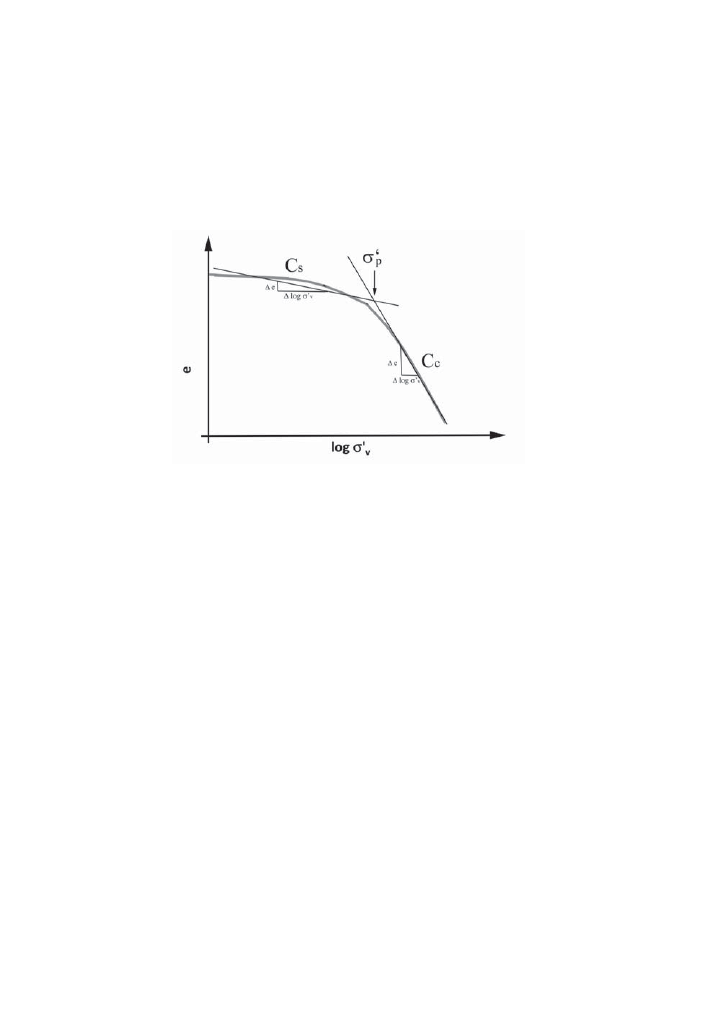
Typowa krzywa

ĞciĞliwoĞci otrzymywana z badania, wykreĞlona w ukáadzie wskaĨnik

porowato

Ğci e — logarytm efektywnego naprĊĪenia pionowego log

v’

v

zosta

áa przedstawiona

na rysunku 1. Krzywa sk

áada siĊ z dwóch podstawowych fragmentów o przebiegu w przybli-

Īeniu liniowym. Pierwsza czĊĞü krzywej przedstawia ĞciĞliwoĞü w zakresie obciąĪeĔ wtórnych
i reprezentuje odkszta

ácenia w przewadze sprĊĪyste. Druga czĊĞü krzywej przedstawia ĞciĞli-

wo

Ğü w zakresie obciąĪeĔ pierwotnych i reprezentuje odksztaácenia w przewadze plastyczne.

Pochylenie pierwszego odcinka krzywej opisywane jest wska

Ĩnikiem odprĊĪenia C

s

, natomiast

drugiego odcinka wska

Ĩnik ĞciĞliwoĞci C

c

. Wska

Ĩniki obliczane są z zaleĪnoĞci [9, 12]:

gdzie:

e — wska

Ĩnik porowatoĞci,

v’

v

— efektywne napr

ĊĪenie pionowe.

* Instytut Geotechniki i Hydrotechniki, Wydzia

á Budownictwa Lądowego i Wodnego, Politechnika Wrocáaw-

ska, Wroc

áaw

,

log

C C

e

c

s

v

v

D

D

=

l

(1)

550

Wska

Ĩniki ĞciĞliwoĞci C

c

i odpr

ĊĪenia C

s

wykorzystywane s

ą do obliczeĔ osiadaĔ pod-

áoĪa gruntowego [1, 6, 9]. W odróĪnieniu od edometrycznego moduáu ĞciĞliwoĞci E

oed

, warto-

Ğci C

c

i C

s

s

ą staáe dla danego gruntu i nie zaleĪne od obciąĪenia co powoduje, Īe są znacznie

ch

Ċtniej stosowane w obliczeniach. GranicĊ zastosowaĔ w obliczeniach wskaĨnika odprĊ-

Īenia C

s

i

ĞciĞliwoĞci C

c

wyznacza napr

ĊĪenie prekonsolidacji

v’

p

(charakterystyczny punkt

za

áamania krzywej ĞciĞliwoĞci (rys. 1).

Wyznaczenie wska

Ĩników C

c

i C

s

w przypadku gruntów drobnoziarnistych ze

wzgl

Ċdu na potrzebny dáugi czas konsolidacji oraz koniecznoĞü pozyskania próby grun-

tu odpowiedniej klasy jako

Ğci jest kosztowne i dáugotrwaáe. W związku z powyĪszym

poszukuje si

Ċ zaleĪnoĞci pomiĊdzy wskaĨnikami C

s

i C

c

a warto

Ğciami charakterystycz-

nych parametrów geotechnicznych, które umo

Īliwią szybsze, wstĊpne oszacowanie

osiada

Ĕ [2, 7, 8, 10, 11, 13–15, 17–21]. Najszerzej znanym równaniem pozwalającym

wyznaczy

ü wartoĞü C

c

jedynie na podstawie warto

Ğci granicy páynnoĞci w

L

jest równa-

nie wska

Ĩnika ĞciĞliwoĞci Skemptona wyprowadzone dla gruntów ilastych o strukturze

przerobionej [19–21]:

Dla gruntów NC — normalnie konsolidowanych, o strukturze naturalnej stosuje si

Ċ

wersj

Ċ poprawioną równania (2) przez Terzaghiego i Pecka [18]:

Wzory (2) i (3) sta

áy siĊ podstawą do dalszych poszukiwaĔ równaĔ wskaĨnika

ĞciĞliwoĞci C

c

[7, 17–21]. Prace [10, 17–18, 21] wykaza

áy, Īe wartoĞü C

c

zale

Īeü

Rys. 1. Krzywa

ĞciĞliwoĞci (C

c

— wska

Ĩnik ĞciĞliwoĞci, C

s

— wska

Ĩnik odprĊĪenia,

v

p

— napr

ĊĪenie prekonsolidacji, e — wskaĨnik porowatoĞci)

,

C

w

0 007

10

c

L

=

-

^

h

(2)

,

C

w

0 009

10

s

L

=

-

^

h

(3)

551

mo

Īe nie tylko od granicy páynnoĞci w

L

, ale równie

Ī od wilgotnoĞci naturalnej w

n

,

wska

Ĩnika porowatoĞci e

0

, czy wska

Ĩnika plastycznoĞci I

p

a tak

Īe wskaĨnika skur-

czalno

Ğci I

S

(tabela 1). Najnowsze badania wskazuj

ą [4, 20–21], Īe wartoĞü C

c

uza-

le

Īniü moĪna równieĪ od wskaĨnika porowatoĞci gruntu e

L

— wyznaczonego dla

tego samego gruntu o strukturze przerobionej i wilgotno

Ğci odpowiadającej granicy

p

áynnoĞci w

L

(tabela 1).

W pracy podj

Ċto próbĊ oceny moĪliwoĞci korzystania z równaĔ wskaĨników ĞciĞliwo-

Ğci dla oceny wartoĞci C

c

i

áów serii poznaĔskiej. Badania przeprowadzono na iáach z rejonu

Wroc

áawia. Wyznaczone z badaĔ wartoĞci wskaĨnika C

c

porównano z warto

Ğciami C

c

wy-

prowadzonymi z niektórych równa

Ĕ z tabeli 1.

2. Materia

á do badaĔ

Do bada

Ĕ wytypowano iáy serii poznaĔskiej z okolic Wrocáawia. Iáy te na nomogra-

mie plastyczno

Ğci Casagrande’a leĪą powyĪej linii A [16]. Grunty te w skáadzie granulo-

metrycznym zawieraj

ą praktycznie tylko frakcje drobne: Cl i Si, z czego frakcji iáowej Cl

od 38,9—76,6%. Sk

áad granulometryczny oraz cechy fi zyczne i wskaĨniki klasyfi kacyjne

analizowanych gruntów przedstawiono w tabeli 2. I

áy te są gruntami prekonsolidowanymi

o cz

Ċsto znacznej wartoĞci ciĞnienia prekonsolidacji

v’

p

[16] (tabela 3).

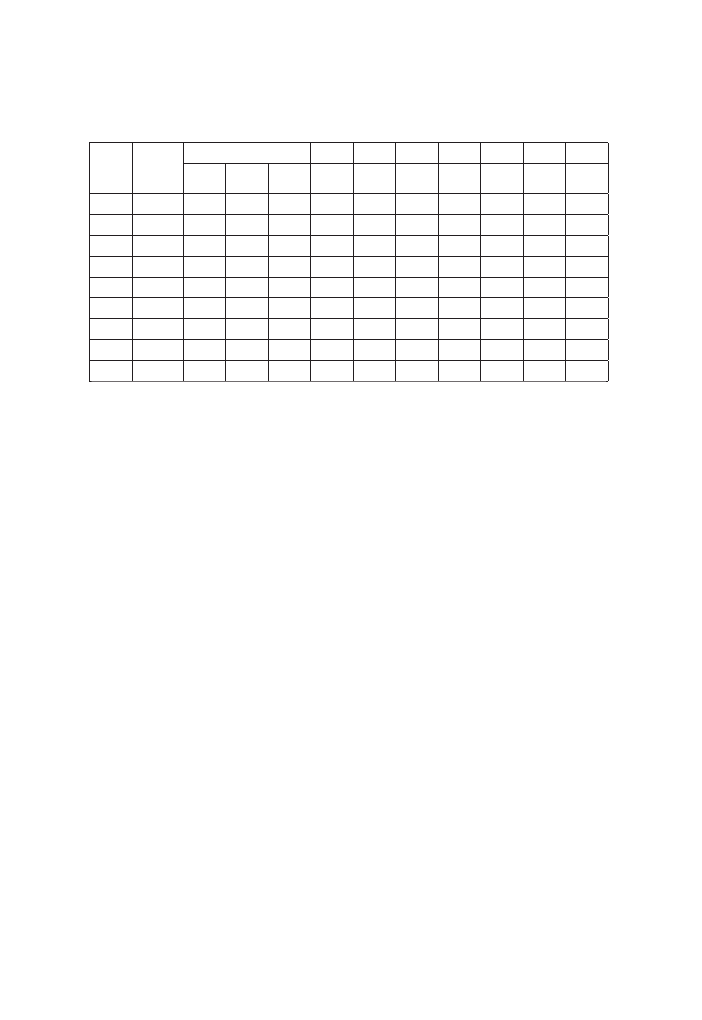
TABELA 1
Równania wska

Ĩnika ĞciĞliwoĞci

C

c

Równanie

Zastosowanie

Autor

C

c

= 0,007 (w

L

– 10)

I

áy przerobione

Skempton – 1944 (por. [19])

C

c

= 0,009 (w

L

– 10)

I

áy naturalne

Terzagi i Peck – 1967 (por. [19])

C

c

= 0,006 (w

L

– 9)

I

áy

Azzouz i in. – 1976 [2]

C

c

= 0,008 (w

L

– 12)

I

áy

Sridharan i Nagaraj – 2000 [18]

C

c

= 0,014 (I

p

+ 3,6)

I

áy

Sridharan i Nagaraj – 2000 [18]

C

c

= 0,007 (I

S

+ 18)

I

áy

Sridharan i Nagaraj – 2000 [18]

C

c

= 0,01 w

n

I

áy

Koppula – 1981 [11]

C

c

= 0,001 (w

n

– 7,519)

I

áy

Herrero – 1983 (por. [18])

C

c

= 0,208 e

0

+ 0,0083

I

áy z Chicago

Bowles 1989 [5]

C

c

= 0,156 e

0

+ 0,0107

I

áy

Bowles 1989 [5]

C

c

= 0,40 (e

0

– 0,25)

I

áy

Azzouz i in. – 1976 [2]

C

c

= 0,5 I

p

G

S

I

áy przerobione i naturalne

Wroth i Wood – 1978 (por. [10])

C

c

= 0,2237 e

L

I

áy przerobione i naturalne

Nagaraj i in. – 1983 [14]

C

c

= 0,2343 e

L

I

áy przerobione i naturalne

Nagaraj i in. – 1986 [14]

C

c

= 0,274 e

L

Mieszanki ilasto–piaszczyste

Nagaraj i in. – 1995 (por. [17])

w

L

— granica p

áynnoĞci, w

n

— wilgotno

Ğü naturalna, e

0

— wska

Ĩnik porowatoĞci, e

L

— wska

Ĩnik porowatoĞci

pasty gruntowej przy wilgotno

Ğci w

L

, I

p

— wska

Ĩnik plastycznoĞci, I

s

— wska

Ĩnik skurczalnoĞci

552

3. Metoda

bada

Ĕ

Analiz

Ċ przeprowadzono na podstawie edometrycznych badaĔ ĞciĞliwoĞci 9 próbek

i

áów. Badania prowadzono procedurą I

L

[9, 16]. Obci

ąĪenia realizowano w edometrach

powy

Īej wartoĞci

v’

p

(tabela 3) a

Ī zaleĪnoĞü pomiĊdzy wskaĨnikiem e a log

v’

v

stawa

áa siĊ

w przybli

Īeniu liniowa. Efekt taki, dla analizowanych gruntów, uzyskiwano zwykle przy ob-

ci

ąĪeniu powyĪej 1–1,5 MPa. ObciąĪenia kontynuowano aĪ do obciąĪenia równego 3,5 MPa.

W analizie uwzgl

Ċdniono tylko te badania, gdzie wartoĞü C

c

po przekroczeniu obci

ąĪenia

v’

p-

stabilizowa

áa siĊ i nie odbiegaáa w trzech kolejnych przedziaáach naprĊĪeĔ wiĊcej niĪ 10%.

4. Wyniki

bada

Ĕ

Warto

Ğci obliczonych wskaĨników C

c

i napr

ĊĪeĔ prekonsolidacji podano w tabeli 3.

Oszacowane z bada

Ĕ edometrycznych wartoĞci wskaĨników C

c

analizowanych gruntów

mieszcz

ą siĊ w przedziale 0,15 do 0,40 i są typowa dla iáów [3]. NajniĪsze wartoĞci C

c

stwier-

dzono dla gruntów o ma

áej początkowej wartoĞci wskaĨnika porowatoĞci e

0

(tabele 2 i 3).

Korelacj

Ċ pomiĊdzy wyznaczonymi z badaĔ wartoĞciami wskaĨnika C

c

a w

L

, w

n

, e

0

oraz

e

L

przedstawiono na rysunku 2.

Analizuj

ąc wyniki badaĔ (rys. 2d) nie zauwaĪono korelacji pomiĊdzy C

c

a e

L

— wska

Ĩ-

nikiem porowato

Ğci pasty gruntowej przy wilgotnoĞci równej w

L

.

S

áaba korelacja jaka pojawia siĊ pomiĊdzy wskaĨnikiem C

c

a w

L

(rys. 2a), mog

ąca byü

wynikiem ma

áego rozrzutu samej wartoĞci w

L

przy du

Īej zmiennoĞci C

c

sugeruje

Īe równania

(2) i (3) nie spe

ániają oczekiwaĔ dla analizowanych gruntów. ZaleĪnoĞü pomiĊdzy C

c

a w

L

— odwrotnie proporcjonalna, jest te

Ī odwrotna do tej jaką uzyskiwano dla past gruntowych

TABELA 2
Warto

Ğci podstawowych cech fi zycznych i wskaĨników klasyfi kacyjnych analizowa-

nych gruntów

Nr

próbki

Rodzaj

gruntu

(ISO)

Frakcje [%]

e

0

e

L

w

n

w

p

w

L

I

p

I

c

Cl [%] Si [%] Sa [%]

[—]

[—]

[%]

[%]

[%]

[—]

[—]

1

Cl

66,9

33,1

0

0,61

1,79

25,20

23,70

67,20

43,50

0,97

2

Cl

64,7

35,3

0

0,60

1,93

23,10

23,40

71,20

47,80

1,01

3

Cl

39,3

60,7

0

0,71

1,35

21,53

23,80

47,90

24,10

1,09

4

Cl

38,9

55,6

5,5

0,90

2,21

26,69

22,30

50,10

27,80

0,84

5

Cl

49,0

48,2

2,8

0,82

2,28

26,60

23,80

47,90

24,10

0,88

6

Cl

76,6

23,4

0

0,64

2,17

19,26

23,00

80,90

57,90

1,06

7

Cl

68,7

31,3

0

0,64

2,30

19,20

25,40

79,00

53,60

1,12

8

Cl

68,0

32,0

0

0,57

1,87

20,30

28,00

70,40

42,40

1,18

9

Cl

70,2

29,8

0

0,51

2,03

19,60

32,00

76,00

44,00

1,28

w

L

— granica p

áynnoĞci, w

n

— wilgotno

Ğü naturalna, e

0

— wska

Ĩnik porowatoĞci, e

L

— wska

Ĩnik porowatoĞci

pasty gruntowej przy wilgotno

Ğci w

L

, I

p

— wska

Ĩnik plastycznoĞci, I

c

— wska

Ĩnik konsystencji

553

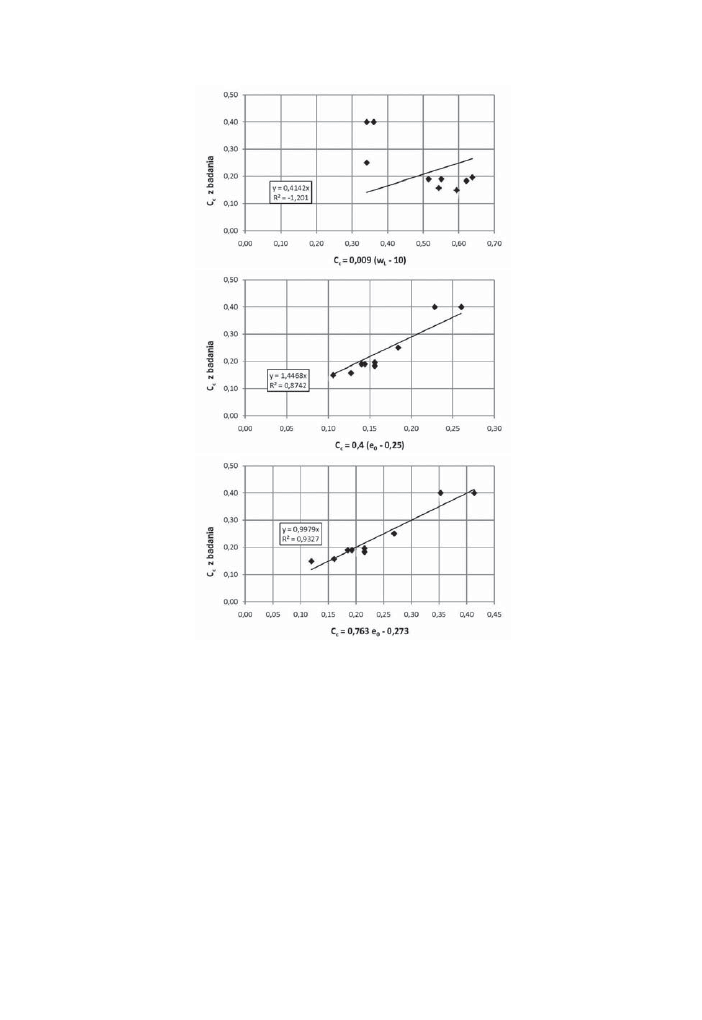
[7, 19–21]. S

áabą korelacjĊ zauwaĪono równieĪ pomiĊdzy C

c

a wilgotno

Ğcią w

n

(rys. 2b).

Najlepsz

ą korelacjĊ stwierdzono pomiĊdzy C

c

a e

0

(rys. 2c) sugerowa

áoby to, Īe równanie

wska

Ĩnika C

c

powinno opiera

ü siĊ na wskaĨniku porowatoĞci e

0

analizowanego gruntu.

W zwi

ązku ze stwierdzonymi zaleĪnoĞciami (rys. 2) sprawdzono dla analizowanych

i

áów stosowalnoĞü wzoru (3) jako najszerzej stosowanego dla iáów oraz równaĔ uzaleĪnio-

nych od wilgotno

Ğci naturalnej w

n

(tabela 1) i przede wszystkim równa

Ĕ opartych na wskaĨ-

niku porowato

Ğci e

0

(tabela 1). Uzyskane warto

Ğci wskaĨników C

c

wyznaczonych z bada

Ĕ

edometrycznych wraz z warto

Ğciami C

c

uzyskanymi z niektórych równa

Ĕ zestawiono w ta-

beli 3. Wybrane zale

ĪnoĞci korelacyjne przedstawiono na rysunku 3.

Stwierdzono,

Īe równanie (3) nie znajduje zastosowania w przypadku iáów serii poznaĔ-

skiej. Uzyskane z (3) warto

Ğci C

c

znacznie odbiegaj

ą od rzeczywistych (tabela 3, rys. 3a)

i w wi

ĊkszoĞci przypadków są znacznie zawyĪone. Równanie oparte na wilgotnoĞci natural-

nej wn (tabele 1 i 3) znacznie lepiej pozwala wyznaczy

ü wartoĞü wskaĨnika C

c

lecz i w tym

przypadku warto

Ğci są zwykle zawyĪone, a w przypadku gruntów o bardzo wysokim e

0

za-

ni

Īone. Najlepszą korelacjĊ z zaprezentowanych równaĔ (tabela 1) uzyskano dla równania

wi

ąĪącego wskaĨnik C

c

z e

0

(rys. 3b) [2]:

Przeprowadzona analiza pozwoli

áa wyznaczyü korelacjĊ pomiĊdzy C

c

a e

0

dla prekon-

solidowanych i

áów serii poznaĔskiej (rys. 2d, rys. 3c, tabela 3) i wyprowadziü równanie

wska

Ĩnika C

c

najlepiej opisuj

ące tĊ zaleĪnoĞü:

TABELA 3
Warto

Ğci wskaĨników ĞciĞliwoĞci analizowanych gruntów

(OED – badanie edometryczne)

Nr

próbki

Rodzaj

gruntu

(ISO)

v’

p

Cc

OED

C

c

= 0,009·

·(

w

L

– 10)

C

c

= 0,01

w

n

C

c

= 0,208

e

0

+

+ 0,0083

C

c

= 0,156

e

0

+

+ 0,0107

C

c

= 0,40·

·(

e

0

– 0,25)

C

c

= 0,763·

·e

0

– 0,273

[kPa]

[—]

1

Cl

750

0,190

0,515

0,252

0,135

0,106

0,140

0,192

2

Cl

770

0,190

0,551

0,231

0,133

0,104

0,140

0,185

3

Cl

670

0,250

0,341

0,215

0,156

0,121

0,184

0,269

4

Cl

680

0,400

0,361

0,267

0,196

0,151

0,260

0,414

5

Cl

910

0,400

0,341

0,266

0,179

0,139

0,228

0,353

6

Cl

700

0,196

0,638

0,193

0,141

0,111

0,156

0,215

7

Cl

710

0,184

0,621

0,192

0,141

0,111

0,156

0,215

8

Cl

480

0,158

0,544

0,203

0,126

0,099

0,127

0,160

9

Cl

420

0,150

0,594

0,196

0,115 10,091 0,106

0,119

,

,

C

e

0 40

0 25

c

0

=

-

^

h

(4)

0,763

,

C

e

0 273

c

0

=

-

(5)

554

Rys. 2. Zale

ĪnoĞü pomiĊdzy wartoĞcią wskaĨnika ĞciĞliwoĞci C

c

wyprowadzon

ą

z bada

Ĕ edometrycznych a: a) w

L

— granic

ą páynnoĞci, b) w

n

— wilgotno

Ğcią naturalną,

c) e

0

— pocz

ątkowym wskaĨnikiem porowatoĞci, d) e

L

— wska

Ĩnikiem porowatoĞci

pasty gruntowej przy wilgotno

Ğci równej w

L

a)

b)

c)

d)

555

5. Wnioski

W przypadku prekonsolidowanych i

áów prawidáowe wyznaczenie wskaĨnika ĞciĞliwo-

Ğci C

c

w laboratorium, wymaga przeprowadzenia bada

Ĕ edometrycznych przy duĪych obcią-

Īeniach — powyĪej

v’

p

— cz

Ċsto znacznie przekraczających zalecenia normowe.

Równania

ĞciĞliwoĞci pozwalają z pewnym przybliĪeniem oszacowaü wartoĞü wskaĨni-

ka

ĞciĞliwoĞci Cc. Zakres stosowania równaĔ jest jednak zwykle ograniczony do okreĞlonej

grupy gruntów. W zwi

ązku z powyĪszym równania te powinny byü wyprowadzane dla kaĪ-

dej grupy niezale

Īnie.

Rys. 3. Zale

ĪnoĞü pomiĊdzy wartoĞcią wskaĨnika ĞciĞliwoĞci C

c

wyprowadzon

ą

z bada

Ĕ edometrycznych a: a) wartoĞcią C

c

obliczon

ą z (3),

b) warto

Ğcią C

c

obliczon

ą z (4), c) wartoĞcią C

c

obliczon

ą z (5)

a)

b)

c)

Z przeprowadzonej analizy wynika,

Īe najszerzej stosowane równanie (3) nazywane

powszechnie równaniem Skemptona w przypadku silnie prekonsolidowanych i

áów serii po-

zna

Ĕskiej nie znajduje zastosowania. Uzyskiwane z równania (3) wartoĞci wskaĨnika C

c

s

ą

zwykle znacznie zawy

Īone — czĊsto ponad dwukrotnie wyĪsze.

Najlepsz

ą korelacjĊ wskaĨnika ĞciĞliwoĞci C

c

analizowanych i

áów stwierdzono wobec

pocz

ątkowej porowatoĞci gruntu e

0

. Z po

Ğród zaprezentowanych równaĔ wyprowadzonych

przez innych autorów dla innego rodzaju i

áów najlepsze przybliĪenie wartoĞci C

c

uzyska

ü

mo

Īna z rozwiązania równania (4) [2].

Przeprowadzona analiza pozwoli

áa wyprowadziü równanie oparte na wskaĨniku porowa-

to

Ğci, które najlepiej przybliĪa wartoĞü wskaĨnika ĞciĞliwoĞci iáów serii poznaĔskiej (5). Rów-

nanie to, mo

Īe sáuĪyü jednak tylko do przybliĪonej oceny wartoĞci wskaĨnika ĞciĞliwoĞci C

c

.

LITERATURA

[1] Aysen A.: Problem solving in soil mechanics. Lisse, Swets and Zeitlinger B.V., 2003

[2] Azzouz A.S., Krizek R.J., Corotis R.B.: Regression Analysis of Soil Compressibility. Soil and

foundations,16, 2, 1976, pp. 19–29

[3] Bell F.G.: Engineering Properties of Soils and Rocks. London, Blackwell Sc. Ltd., 2000
[4] Burland J.B.: On the Compressibility and Shear Strength of Natural Soil. Geotechnique, 40,

3, 1990, pp. 329–378

[5] Bowles J.E.: Physical and Geotechnical Properties of Soils. McGraw–Hill Company Inc., New York, 1989
[6] Craig F.R.: Soil Mechanics. Taylor and Francis, New York, 2004

[7] Giasi C.I., Cherubini C., Paccapelo F.: Evaluation of Compression Index of Remoulded Clays

by Means of Atterberg Limits. Bull. Eng. Geol. Env., 62, 2003, pp. 233–340

[8] Gregory A.S. i in.: Calculation of Compression Index and Precompression Stress from Soil

Compression Test Data. Soil and Tillage Res., 89, 2006, pp. 45–57

[9] Lambe T.W., Whitmann R.V.: Mechanika gruntów. Arkady, Warszawa, 1977

[10] Lav M.A., Ansal A.M.: Regression Analysis of Soil Compressibility. Turk J. Engin. Environ.

Sci., 25, 2001, pp. 101–109

[11] Koppula S.D.: Statistical Estimation of Compression Index. Geotechnical Testing J.,4, 2, 1981, pp. 68–73

[12] Mitchell J.K., Soga K.: Fundamental of Soil Behavior. John Willey and Sons, London, 2005
[13] Ozer M., Isik N.S., Orhan M.: Statistical Neural Network Assessment of the Compression

Index of Clay-bearing Soils. Bull. Eng. Geol. Environ., 67, 2008, pp. 537–545

[14] Nagaraj T.S., Srinivasa Murthy B.R.: A Critical Reappraisal of Compression Index Equation.

Geotechnique, 36, 1, 1986, pp. 27–32

[15] Park J.H., Koumoto T.: New Compression Index Equation. J. Geotech. Geoenv. Eng., 130, 2,

2004, pp. 223–226

[16] Stró

Īyk J.: Przyczyny prekonosolidacji iáów formacji poznaĔskiej z rejonu poáudniowo–za-

chodniej Polski. Praca doktorska. Instytut Geotechniki i Hydrotechniki, Wroc

áaw, 2004

[17] Sridharan A., Gurtug Y.: Compressibility Characteristics of Soil. Geotech. Geol. Eng., 23,

2005, pp. 615–634

[18] Sridharan A., Nagaraj H. B.: Compressibility Bahaviour of Remoulded, Fine-grained Soils

and Correlation with Index Properties. Can. Geotech. J., 37, 3, 2000, pp. 712–722

[19] Terzaghi K., Peck R.B.: Soil Mechanics in Engineering Practice. John Wiley Inc., New York, 1996

[20] Tripathy S., Mishra A.K.: On the use of Skempton’s Compression Index Equation. Geotech.

Geol. Eng., 29, 2011, pp. 129–125

[21] Yoo G. L., Kim B.T., Jeon S.S.: Empirical Correlations of Compression Index for Marine Clay

from Regression Analysis. Can. Geotech. J., 41, 2004, pp. 1213–1221