1. Wstęp teoretyczny

Średnie odległości cząsteczek w cieczach są znacznie mniejsze niż w gazach, dlatego siły wzajemnego ich oddziaływania odgrywają istotną rolę. Zasięg działania tych sił jest bardzo mały, rzędu 5*10^-8 m, a więc około 50 średnic cząsteczki. Na cząsteczki cieczy znajdujące się w warstwie powierzchniowej pozostała część cząsteczek wywiera siłę przyciągania skierowaną w głąb cieczy i prostopadłą do jej powierzchni. Dlatego powierzchniowa warstwa wywiera na ciecz wielkie ciśnienie wewnętrzne dochodzące do dziesiątków tysięcy atmosfer ( dla wody ~1700 at.). Ciśnienia wewnętrznego nie można zmierzyć doświadczalnie, gdyż zawsze skierowane jest w głąb cieczy, a więc nie działa na ścianki naczynia i na ciała w niej zanurzone.

Średnia energia kinetyczna cząsteczek określana jest wyłącznie przez temperaturę. Dlatego w stanie równowagi energie cząsteczek warstwy powierzchniowej i znajdujących się wewnątrz cieczy są identyczne. Natomiast energia potencjalna uwarunkowana jest siłami wzajemnego oddziaływania międzycząsteczkowego. Cząsteczka przechodząc z wewnętrznych części cieczy na jej powierzchnię musi wykonać pracę przeciwko jej siłom przyciągania skierowanym w głąb cieczy. Dlatego cząsteczki warstwy powierzchniowej mają większą energię potencjalną niż cząsteczki wewnątrz cieczy.

Właściwsze i precyzyjniejsze niż pojęcie energii potencjalnej jest pojęcie energii swobodnej ciała, które jest miarą maksymalnej pracy jaką mogłoby ciało wykonać w odwracalnym procesie izotermicznym. W przybliżeniu można je oczywiście utożsamiać z energią potencjalną. Z termodynamiki wynika, że w stanie równowagi stałej układ zachowuje się tak, że posiada minimalną wartość energii swobodnej. Dlatego każda ciecz w stanie równowagi zachowuje się tak, aby mieć najmniejsze pole powierzchni. Świadczy to o tym, że warstwa powierzchniowa jest podobna do rozciągniętej błonki sprężystej. Działają w niej siły molekularne leżące w płaszczyźnie powierzchni cieczy i skierowane na wszystkie jej strony - są to siły napięcia powierzchniowego.

Ze wzoru F = 2 δ l wynika, że wartość liczbowa współczynnika napięcia powierzchniowego równa się sile działającej na jednostkę długości obwodu ograniczającego powierzchnię cieczy. Siła ta jest spowodowana wzajemnym przyciąganiem między cząsteczkami warstwy powierzchniowej i jest skierowana wzdłuż stycznej do powierzchni oraz prostopadle do obwodu. W układzie SI jednostką napięcia powierzchniowego jest więc N/m.

Wyznaczanie napięcia powierzchniowego cieczy przeprowadzane jest trzema metodami:

1) przez rozrywanie błonki powierzchniowej wskutek jej rozciągnięcia;

2) przez pomiar wzniesienia włoskowatego w rurkach włoskowatych (kapilarach);

3) na podstawie wypływu kroplowego.

W naszym ćwiczeniu korzystamy z drugiej metody.

Zakrzywiona swobodna powierzchnia cieczy przy ściankach naczynia nazywa się meniskiem. W celu jego scharakteryzowania wprowadza się pojęcie kąta granicznego θ między zwilżoną powierzchnią ścianki i meniskiem w punktach ich przecięcia się. Jeżeli θ < 90⁰ mówimy, że ciecz zwilża ściankę, jeżeli θ > 900 (rys.9.3b) mówimy, że ciecz nie zwilża ścianki.

Występowanie menisku jest spowodowane tym, że cząsteczki cieczy znajdujące się w pobliżu ścianki ciała stałego oddziałują z jego cząsteczkami.

Pierre Laplace wprowadził następującą zależność między ciśnieniem Pk, wywieranym na ciecz przez warstwę powierzchniową, dzięki działaniu sił napięcia powierzchniowego a geometrią powierzchni cieczy:

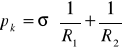
gdzie: R1 i R2 oznaczają promienie krzywizn dwóch dowolnych, ale wzajemnie prostopadłych

przekrojów normalnych w danym punkcie cieczy.

Przekrojem normalnym powierzchni w danym punkcie nazywamy krzywą otrzymaną w przecięciu powierzchni płaszczyzną przechodzącą przez normalną (prostopadłą) do powierzchni w tym punkcie. R1 lub R2 przyjmuje się za dodatnie, gdy środek krzywizny przekroju leży wewnątrz cieczy.

Dla powierzchni kulistej R1= R2=R, więc:

Dla kapilary o małym promieniu r powierzchnia cieczy jest kulista, przy czym jej promień:

Dla cieczy z meniskiem wklęsłym ciśnienie Pk jest równoważone ciśnieniem hydrostatycznym słupa cieczy w kapilarze:

Pk = ρ g h

gdzie: ρ - gęstość cieczy; h - wysokość słupa cieczy w kapilarze mierzona od poziomu cieczy w naczyniu; g - przyśpieszenie ziemskie.

Zestawiając trzy powyższe wzory otrzymujemy możliwość wyznaczenia spółczynnika napięcia powierzchniowego cieczy badając efekt kapilarny:

2. Wykonywanie czynności i wyniki pomiarów

Opis układu pomiarowego

W skład układu pomiarowego wchodzą trzy naczynia napełnione badanymi cieczami. Do każdego z nich wstawiona jest pionowa kapilara. Naczynie z badaną cieczą ustawia się na stoliczku z regulowaną wysokością. Do zmierzenia wysokości słupa cieczy służy katetometr, tzn. przyrząd do wyznaczania pionowych odległości między punktami. Składa się on z kilku podstawowych elementów:

• masywnego pręta umocowanego na trójnożnej podstawie ze śrubą regulującą pionowe ustawienie katetometru; na pręcie naniesiona jest skala milimetrowa;

• lunetki, w polu widzenia której znajdują się dwie skrzyżowane nici ( przy pomiarach punkt przecięcia nici należy nastawić na wybrane poziomy - dolny menisk cieczy w kapilarze i na dolny menisk cieczy w naczyniu).

Lunetka przymocowana jest do cylindra obejmującego pręt katetometru. Cylinder ten wraz z lunetką można z łatwością przesuwać wzdłuż pręta i zamocować za pomocą odpowiedniej śruby w wybranym miejscu. W cylindrze zrobione jest prostokątne wycięcie dla odczytu na skali milimetrowej położenia lunetki. Położenie to może być określone z dokładnością do 0,05 milimetra, dzięki skali noniusza umieszczonej wzdłuż wycięcia.

Przeprowadzenie eksperymentu

1. Zapoznać się z budową katetometru.

2. Ustawić stoliczek w odległości około 2 m. Umieścić na mim naczynie z badaną cieczą. Dobrać odpowiednią wysokość pozwalającą na swobodne dokonywanie odczytów poziomów cieczy na skali katetometru.

3. Zmierzyć wysokość słupa cieczy h w kapilarze. Wykonać co najmniej 5 pomiarów.

4. Wykonać pomiary według punktów 2 i 3 dla dwóch pozostałych cieczy.

5. Odczytać jaka jest temperatura w pomieszczeniu.

6. Zanotować wartość promienia kapilary r podaną w instrukcji załączonej do układu pomiarowego.

Wyniki pomiarów

	Wysokość	słupa	cieczy (cm)
Numer pomiaru	Woda	Benzen	Toluen
1	4,09	1,81	1,75
2	4,00	1,76	1,77
3	4,12	1,79	1,78
4	4,03	1,72	1,72
5	3,99	1,72	1,77
Średnia	4,046	1,760	1,758

Tab. 1 Wyniki pomiarów

3. Obliczenia i analiza dokładności wyników

Dla obliczonych wartości h_śr obliczam współczynniki napięcia powierzchniowego poszczególnych cieczy ze wzoru:

przyjmując następujące dane:

r_kapilary = 0,25 mm ± 0,001 mm T_otoczenia = 21ºC

p_otoczenia = 754 mm Hg g = 9,8066 m/s² θ = 0

ρ_wody = 0,99802 g/cm³ ρ_benzenu = 0,8790 g/cm³ ρ_toluenu = 0,8668 g/cm³

h_{śr wody} = 4,046 cm h_{śr benzenu} = 1,760 cm h_{śr toluenu} = 1,758 cm

σ_wody = 0,04949 N/m

σ_benzenu = 0,01896 N/m

σ_toluenu = 0,01868 N/m

obliczam odchylenie standardowe od obliczonej wartości h_śr nazywane błędem średnim kwadratowym punktów, na podstawie wzoru:

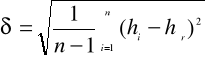
δ_W = 5,683 * 10 ^-4 m

δ_B = 4,062 * 10 ^-4 m

δ_T = 2,387 * 10 ^-4 m

Obliczamy odchylenie standardowe dla współczynnika napięcia powierzchniowego, jako wartości wyznaczonej w sposób pośredni, na podstawie ogólnego wzoru w postaci:

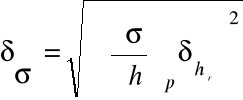
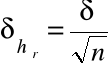
który w tym przypadku przyjmuje postać :

δ_σW = 0,000697 N/m

δ_σB = 0,000438 N/m

δ_σT = 0,000254 N/m

Obliczam przedział ufności ze wzoru:

odpowiadający prawdopodobieństwu 95% k_p = 1,96

Δδ_σW = 0.001366 N/m

Δδ_σB = 0.000858 N/m

Δδ_σT = 0.000498 N/m

4. Wnioski końcowe

Na wynik pomiarów ma wpływ jedynie błąd pomiaru wysokości słupa cieczy, który jest przypadkowy i stosunkowo niewielki, dlatego błędy obliczeń napięcia powierzchniowego są również znikome, rzędu maksymalnie 5%. Wpływ na pewne rozbieżności w wynikach mogło mieć również utracenie przez substancje swych wzorcowych właściwości.

Wartości h_śr obliczone na podstawie wzoru:

---