Laboratorium fizyki

Wyznaczanie bezwładności ciał metodą wahadła

fizycznego grawitacyjnego i sprawdzanie twierdzenia Steinera

Patryk Wojciechowski, Wydział Elektroniki, Data: 17 kwietnia 1998

Cel ćwiczenia:

Celem ćwiczenia było stwierdzenie zależności między okresem drgań wahadła fizycznego grawitacyjnego i momentem bezwładności ciała. Należało też doświadczalnie sprawdzić słuszność twierdzenia Steinera oraz wyznaczyć momenty bezwładności różnych brył.

Wstęp teoretyczny;

Miarą bezwładności bryły sztywnej w ruchu obrotowym jest tak zwany moment bezwładności. Moment ten wyraża się względem wybranej osi, najczęsciej jest to oś symetrii. Jest to analogicznie do tego jak masa stanowi miarę bezwładności ciała w ruchu postępowym. Wielkość ta nie zależy tylko od masy ciała, jego kształtu i wielkości ale także od położenia bryły względem osi obrotu. Ogólny wzór na moment dowolnej bryły ma postać:

Z momentem bezwładności związane jest twierdzenie Steinera. Mówi ono że: moment bezwładności bryły względem dowolnej osi jest równy sumie momentu bezwładności względem osi przechodzącej przez środek masy równolegle do rozważanej osi oraz iloczynu masy bryły i kwadratu odległości między osiami:

Ponieważ wahające się ciało jest wahadłem fizycznym spełniony musiał być warunek sinα=α, co uzyskaliśmy przez małe drgania bryły. Moment bezwładności względem wybranej osi obliczaliśmy mierząc okres tych drgań względem danej osi, następnie wyznaczaliśmy moment bezwładności korzystając z zależności:

Chcąc wyznaczyć moment bezwładności bryły względem osi przechodzącej przez jej środek masy, a dysponując okresem drgań bryły względem innej osi obliczamy stałą wahadła grawitacyjnego określoną wzorem:

a następnie podstawiamy do wzoru:

Układ pomiarowy:

Dwie bryły metalowe : cylindryczny pierścień i tarczę metalową z symetrycznie wywierconymi otworami należało zawieszać na poziomej pryzmatycznej belce i wprawiać w drgania o niewielkiej amplitudzie. Po pomiarze 100 wahnięć bryły należało zmienić w przypadku tarczy otwór, na którym była ona zawieszona i dokonać kolejnych pomiarów. Następnie zmierzyliśmy masę brył za pomocą wagi elektronicznej i odległości między osią wahadła i osią symetrii brył za pomocą suwmiarki.

Wyniki pomiarów:

1. Pierścień metalowy:

średnica wewnętrzna: średnica zewnętrzna:

105,44mm		119,94mm
105,20mm		119,72mm
105,40mm		120,02mm
105,20mm		119,72mm
105,37mm		119,72mm
średnia: 105,322mm		średnia: 119,838mm
promień R1=52,66mm		promień R2=59,919mm

okres 100 wahnięć:

67,24s

67,24s

67,31s

średnia: 67,26s

okres 1 wahnięcia T=0,6726s

masa: 220,4g

Moment bezwładności względem osi zawieszenia:

, gdzie d=R₁=52,66mm

Z twierdzenia Steinera:

Chcąc stwierdzić prawdziwość twierdzenia Steinera liczymy bezwładność ze wzoru tablicowego:

Różnica pomiędzy momentem wyznaczonym metodą statyczną a dynamiczną wynosi:

Dokładność pomiaru momentu bezwładności oceniliśmy metod różniczki zupełnej:

ΔT=0,01s, Δm.=0,1g, Δd=0,1mm

2.Tarcza z otworami.

masa: 1061,5g średnica zewnętrzna D=160,31mm ⇒ R=80,155mm

średnica pomiarowa 2: okres 100 wahnięć względem 2 średnicy:

100,13mm		68,31s
100,21mm		68,26s
100,29mm		68,29s
100,13mm		średnia: 68,2867s
średnia: 100,19mm		okres T2=0,682867s
d2=50,095mm

średnica pomiarowa 3: okres 100 wahnięć względem 3 średnicy:

149,59mm		69,40s
149,58mm		69,38s
149,60mm		69,41s
149,59mm		średnia: 69,3869s
średnia: 149,59mm		okres T3=0,693869s
d3=74,795mm

średnia pomiarowa 4: okres 100 wahnięć względem 4 średnicy:

118,58mm		68,06s
118,59mm		68,07s
118,60mm		68,04s
118,59mm		średnia: 68,0567s
średnia: 118,59mm		okres T4=0,680567s
d4=59,295mm

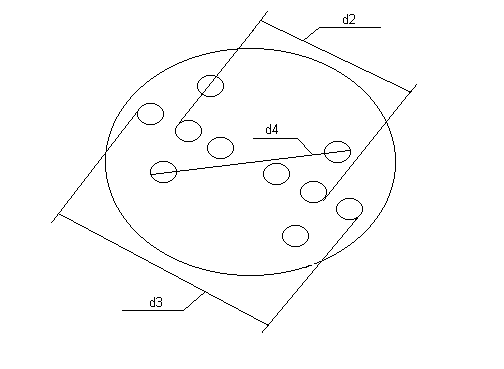
Rysunek: Umiejscowienie badanych średnic na tarczy.

Obliczamy stałe drgań wahadła ze wzoru:

C₂=0,130087m²

C₃=0,132508m²

C₄=0,130617m²

Obliczamy C średnie: 0,131071m²

Na podstawie wzoru:

obliczamy średni moment bezwładności względem osi środkowej.

I_c=0,0035242kgm²

W celu sprawdzenia twierdzenia Steinera, obliczamy momenty bezwładności tarczy względem poszczególnych osi:

I₂=0,00616163 kgm²

I₃=0,00949853 kgm²

I₄=0,00724417 kgm²

a następnie stosujemy je do wzoru Steinera:

I_c2=0,0034978 kgm²

I_c3=0,0035629 kgm²

I_c4=0,0035121 kgm²

Różnice pomiędzy średnim momentem a poszczególnymi momentami obliczonymi przez nas wynoszą odpowiednio:

I_c2-I_c=0,0000264 kgm²

I_c3-I_c=-0,0000386 kgm²

I_c4-I_c=0,0000121 kgm²

Obliczyliśmy także moment bezwładności względem osi środkowej ze wzoru tablicoego:

Dokładność pomiaru momentu bezwładności i stałej C oceniliśmy metod różniczki zupełnej:

ΔT=0,01s, Δm.=0,1g, Δd=0,1mm

Wnioski:

Wyniki pomiarów dokonanych podczas ćwiczenia potwierdzają słuszność twierdzenia Steinera. Dodatkowym argumentem jest uzyskana bardzo mała różnica pomiędzy pomiarem statycznym a dynamicznym, występująca dopiero na trzecim miejscu za pierwszą znaczącą cyfrą. Różnicę tę można wytłumaczyć metodą pomiaru okresu drgań (stoper).Zaistniały bowiem trudności związane z jednakowym ustaleniem momentu startu i zatrzymaniem stopera w poszczególnych pomiarach. Nie bez znaczenia było też tarcie, występujące między powierzchnią pryzmy a zawieszoną bryłą.

Wyprowadzenie wzoru na środkowy moment bezwładności wydrążonego walca.

Walec ten dzielimy na nieskończenie wiele obręczy o grubości `ds.' i momencie bezwładności równym: I=mr²

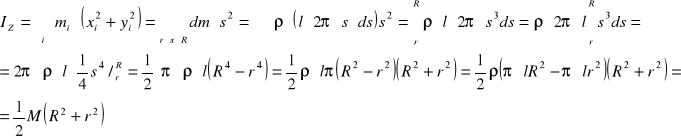
gdzie, M. oznacza całkowitą masę walca, ρ gęstość materiału z którego wykonany jest walec.

1

6

---