UR – nowoczesność i przyszłość regionu
Projekt współfinansowany przez Unię Europejską w ramach Europejskiego Funduszu Społecznego
Uniwersytet Rzeszowski, al. T. Rejtana 16c, 35-959 Rzeszów
s. 1/7
Biuro Projektu: budynek A1, pokój 024, tel. + 48 17 872 11 84
www.nipr.univ.rzeszow.pl,
nipr@univ.rzeszow.pl
Pracownia „Wprowadzenie do metrologii”
Instrukcja do ćwiczeń laboratoryjnych
Ć
wiczenie nr 2
Wyznaczanie g
ę
sto
ś
ci ciał stałych o kształtach
regularnych przy u
ż
yciu mierników długo
ś
ci
i wag o ró
ż
nej klasie dokładno
ś
ci
Krzysztof Kucab
Uniwersytet Rzeszowski
UR – nowoczesność i przyszłość regionu
Projekt współfinansowany przez Unię Europejską w ramach Europejskiego Funduszu Społecznego
Uniwersytet Rzeszowski, al. T. Rejtana 16c, 35-959 Rzeszów
s. 2/7
Biuro Projektu: budynek A1, pokój 024, tel. + 48 17 872 11 84
www.nipr.univ.rzeszow.pl,
nipr@univ.rzeszow.pl
I.
Wstęp teoretyczny
1.
Gęstość ciała (masa właściwa)
ρ
to stosunek masy ciała (m) do zajmowanej
przez nie objętości (V):
m
V
ρ
=
.
Gęstość ciała podajemy w jednostkach [m]/[V], czyli np. [g/cm
3
], [kg/dm
3
],
itp. Jednostką gęstości w układzie SI jest [kg/m
3
].
Tabela 1. Gęstości ciał
*
:
Substancja
ρ
[kg/m
3
]
wodór
0.090
powietrze
1.293
tlen
1.429
chlor
3.22
alkohol etylowy
790
aceton
791
woda (20
o
C)
998.099
gliceryna
1260
rtęć
13550
glin (aluminium)
2720
żelazo
7875
mosiądz
8400-8700
miedź
8933
ołów
11 300-11 400
2.
W celu wyznaczenia objętości niektórych brył geometrycznych wystarczy
zmierzyć ich podstawowe wymiary (np. wysokość, szerokość i głębokość dla
prostopadłościanu). Podstawowymi przyrządami pomiarowymi (dla
pomiarów długości) na I Pracowni Fizycznej są linijka, suwmiarka oraz śruba
mikrometryczna. Przyjmujemy, że maksymalny błąd bezwzględny dla linijki
jest równy najmniejszej podziałce na niej naniesionej.
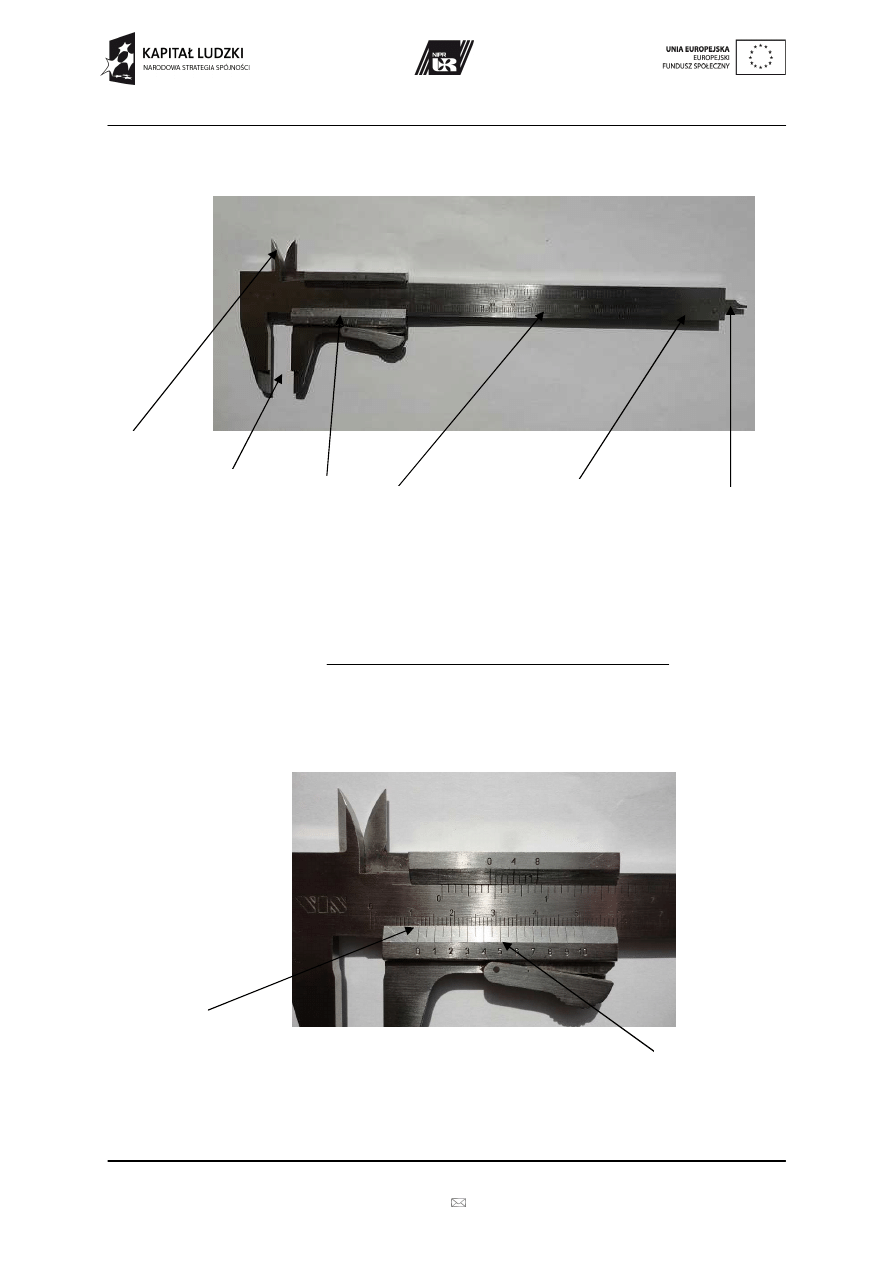
Suwmiarka to przyrząd służący do pomiarów długości z dokładnością do
0.02mm (przeważnie 0.1mm i 0.05mm). Zdjęcie suwmiarki przedstawia
rysunek nr 1.
*
Źródło: Tablice matematyczne, fizyczne, chemiczne i astronomiczne, WSiP, Warszawa 1974.
UR – nowoczesność i przyszłość regionu
Projekt współfinansowany przez Unię Europejską w ramach Europejskiego Funduszu Społecznego
Uniwersytet Rzeszowski, al. T. Rejtana 16c, 35-959 Rzeszów
s. 3/7
Biuro Projektu: budynek A1, pokój 024, tel. + 48 17 872 11 84
www.nipr.univ.rzeszow.pl,
nipr@univ.rzeszow.pl
Rys. 1. Suwmiarka
Maksymalny błąd bezwzględny (
∆
) dla pomiarów dokonywanych
suwmiarką można obliczyć z zależności:
najmniejsza jednostka skali nieruchomej
liczba dzialek (kresek) na noniuszu
∆ =
.
Przykładowy odczyt długości (d) dla suwmiarki (patrz rys. 2.):
Rys. 2. Odczyt z suwmiarki
11mm
0.50mm
d
=
+
=
11.50mm
.
linijka
głębokościomierz
szczęki do pomiaru
średnic wewnętrznych
noniusz
szczęki do pomiaru
średnic zewnętrznych
dokładność suwmiarki
(maks. błąd bezwzględny)
kreska ‘0’ „przechodzi”
poza 11 mm.
kreska ‘5’ leży w jednej linii z kreską
podziałki milimetrowej
UR – nowoczesność i przyszłość regionu
Projekt współfinansowany przez Unię Europejską w ramach Europejskiego Funduszu Społecznego
Uniwersytet Rzeszowski, al. T. Rejtana 16c, 35-959 Rzeszów
s. 4/7
Biuro Projektu: budynek A1, pokój 024, tel. + 48 17 872 11 84
www.nipr.univ.rzeszow.pl,
nipr@univ.rzeszow.pl
Śruba mikrometryczna to przyrząd służący do pomiarów długości
z dokładnością do 0.01mm. Zdjęcie śruby mikrometrycznej przedstawia
rysunek nr 3.
Rys. 3. Śruba mikrometryczna
Przykładowy odczyt długości (d) dla śruby mikrometrycznej (patrz rys. 4.):
Rys. 4. Odczyt ze śruby mikrometrycznej
d = 2mm+0.5mm+0.26mm = 2.76mm.
3.
Do pomiarów masy (ciężaru) ciał służy waga. W ćwiczeniu używamy wagi
szalkowej, przedstawionej na rysunku 5.
wrzeciono
tuleja
bęben
sprzęgło
kowadełko
bęben odsłonił dwa milimetry
bęben odsłonił dodatkowo
pół milimetra
pozioma kreska na tulei jest
przedłużeniem 26 działki bębna
UR – nowoczesność i przyszłość regionu
Projekt współfinansowany przez Unię Europejską w ramach Europejskiego Funduszu Społecznego
Uniwersytet Rzeszowski, al. T. Rejtana 16c, 35-959 Rzeszów
s. 5/7
Biuro Projektu: budynek A1, pokój 024, tel. + 48 17 872 11 84
www.nipr.univ.rzeszow.pl,
nipr@univ.rzeszow.pl
Rys. 5. Waga szalkowa
- Przed przystąpieniem do ważenia należy najpierw wypoziomować
(poziomica) oraz wyzerować (śruby korekcyjne) wagę.
- Badane ciało kładziemy na jednej szalce, odważniki na drugiej.
- Zarówno badane ciało jak i odważniki powinny znajdować się pośrodku szalki.
- Zdejmowanie bądź nakładanie badanego ciała oraz odważników powinno
odbywać się przy zabezpieczonej wadze (pokrętło do aretowania).
- Jeżeli podczas pomiaru wskazówka wychyla się w obie strony wokół zera
o jednakową ilość działek na podziałce, możemy zakończyć ważenie.
- Odważniki powinno się nakładać od względnie najcięższego (za pomocą
pęsety).
II.
Przebieg ćwiczeń
1.
Za pomocą wagi laboratoryjnej (belkowej) trzykrotnie zważyć badany
przedmiot.
2.
Zmierzyć za pomocą linijki wymiary geometryczne figury niezbędne do
wyznaczenia jej objętości. Pomiary każdego wymiaru wykonać trzykrotnie.
W przypadku, gdy otrzymane wyniki któregokolwiek z wymiarów nie
powtarzają się, serię pomiarową rozszerzyć do dziesięciu.
szalka
belka
wskazówka
pryzmat
poziomica
pokrętło do zabezpieczania
(aretowania) wagi
podziałka
wykręcana nóżka
śruby korekcyjne
UR – nowoczesność i przyszłość regionu
Projekt współfinansowany przez Unię Europejską w ramach Europejskiego Funduszu Społecznego
Uniwersytet Rzeszowski, al. T. Rejtana 16c, 35-959 Rzeszów
s. 6/7
Biuro Projektu: budynek A1, pokój 024, tel. + 48 17 872 11 84
www.nipr.univ.rzeszow.pl,
nipr@univ.rzeszow.pl
3.
Wyniki pomiarów umieścić w tabelach
Tabela 2.
L.p.
m [g]
1
2
3
Tabela 3.
schematyczny rysunek badanego
przedmiotu ze wskazaniem
mierzonych wymiarów
geometrycznych
L.p.
a[mm]
b[mm]
...
1
2
..
.
4.
Wykonać serię dziesięciu pomiarów wymiarów geometrycznych badanego
przedmiotu (analogicznie jak w punkcie 2) wykorzystując suwmiarkę oraz
śrubę mikrometryczną. Wyniki zapisać w tabeli.
5.
Obliczyć gęstość materiału badanego przedmiotu.
III.
Informacje uzupełniające
1.
Ze względu na mały błąd względny wnoszony przez pomiar masy, można
ograniczyć się do trzech pomiarów masy badanego ciała. Jako wynik
końcowy należy przyjąć średnią arytmetyczną pomiarów, zaś jako błąd
pomiaru masy:
∆
m = 0.01 g.
2.
Po każdorazowym pomiarze masy ciała, zdejmujemy odważniki oraz
badane ciało, sprawdzamy czy waga jest wyzerowana, następnie kładziemy
ważone ciało na szalce, na której poprzednio znajdowały się odważniki
i rozpoczynamy cały proces ważenia od początku.
3.
Pomiaru wymiarów geometrycznych dokonujemy w różnych miejscach
badanej bryłki.
UR – nowoczesność i przyszłość regionu
Projekt współfinansowany przez Unię Europejską w ramach Europejskiego Funduszu Społecznego
Uniwersytet Rzeszowski, al. T. Rejtana 16c, 35-959 Rzeszów
s. 7/7
Biuro Projektu: budynek A1, pokój 024, tel. + 48 17 872 11 84
www.nipr.univ.rzeszow.pl,
nipr@univ.rzeszow.pl
IV.
Dla dociekliwych
W przypadku, gdy wyniki próbnej serii pomiarów się powtarzają, możemy
przyjąć że dominują błędy systematyczne. W takim przypadku zwiększanie
liczby pomiarów mija się z celem (dla zwiększenia dokładności pomiarów
należy zmienić przyrząd pomiarowy na dokładniejszy). Jako niepewność
pomiarową wielkości mierzonej bezpośrednio przyjmujemy niepewność
przyrządu pomiarowego. W celu obliczenia niepewności pomiarowych
wielkości złożonych stosujemy metodę różniczki zupełnej (ew. pochodnej
logarytmicznej).
W przypadku, gdy wyniki próbnej serii pomiarów różnią się, celowym jest
zwiększenie liczby pomiarów (u nas do dziesięciu). Jako wynik pomiaru
wielkości mierzonej bezpośrednio przyjmujemy średnią arytmetyczną
pomiarów, zaś jako niepewność pomiarową tej wielkości przyjmujemy
odchylenie standardowe średniej arytmetycznej
x
S
. W celu obliczenia
niepewności pomiarowych wielkości złożonych stosujemy odchylenie
standardowe średniej wielkości mierzonej pośrednio. Jako wynik końcowy
niepewności pomiarowej przyjmujemy iloczyn odchylenia standardowego
przez współczynnik Studenta-Fishera (uwzględniający liczbę pomiarów oraz
poziom ufności).
Obliczenia w Laboratorium przeważnie odbywają się dla n=10 pomiarów
oraz przy poziomie ufności 1-
α
= 0.683. W tym przypadku współczynnik
Studenta wynosi
,
1.0585
n
t
α
=
.
V.
Zalecana literatura
1.
H. Szydłowski, Pracownia fizyczna, PWN, Warszawa 1999.
2.
J. Smela, T. Zamorski, A. Puch, Pierwsza pracownia fizyczna - przewodnik,
Wydawnictwo Oświatowe FOSZE, Rzeszów 1995.
3.
J.R. Taylor, Wstęp do analizy błędu pomiarowego, PWN, Warszawa 1999.
4.
J. Rakowiecki, Podstawy metrologii, PWSZ, Katowice 1972.
5.
T. Dryński, Ćwiczenia laboratoryjne z fizyki, PWN, Warszawa 1980.
6.
Sz. Szczeniowski, Fizyka doświadczalna, cz. 1, PWN, Warszawa 1980.