IV/11 Charakterystyka ustrojów powierzchniowych, założenia obliczeniowe/wielkości uogólnione i zależności
między nimi, warunki brzegowe.

Ustroje powierzchniowe charakteryzują się dużą nośnością i korzystnymi własnościami mechanicznymi. W tych ustrojach jeden z wymiarów (grubość) jest wyraznie mniejszy od pozostałych. Ustrój powierzchniowy jest ograniczony powierzchniami górną, dolną i boczną.

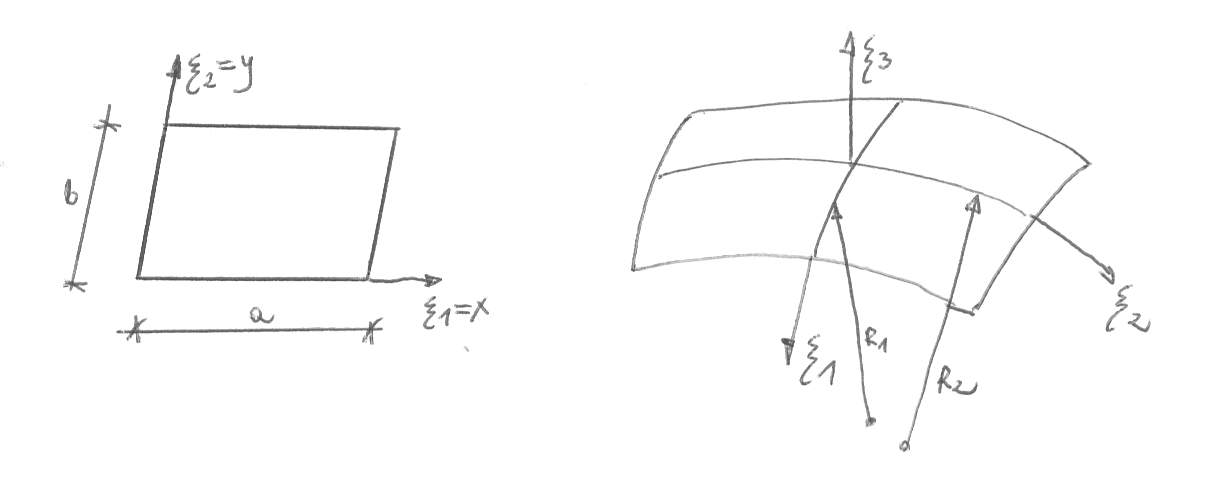
Taką samą rolę jak oś pręta pełni w teorii ustrojów powierzchniowych powierzchnia środkowa, równoległa do powierzchni górnej i dolnej. Grubość h jest najkrótszą odległością pomiędzy powierzchnią górną i dolną, odmierzoną wzdłuż prostej normalnej do powierzchni środkowej. Ustrój powierzchniowy, w którym powierzchnia środkowa jest płaszczyzną nazywamy płytą, a powłoką, jeśli powierzchnia jest zakrzywiona.

Dla płyt

Gdy
<< 1 gdzie l = min(l
,l
) l- charakterystyczny wymiar powierzchni środkowej.

Dla powłok

Gdy
<
do
gdzie R
,R
promienie krzywizny

W ustrojach cienkich wszystkie rozwiązania odnosimy do powierzchni środkowej , opisywanej dwoma niezależnymi parametrami
,
dlatego problemy analizy tych ustrojów są geometrycznie dwuwymiarowe.

Ustroje powierzchniowe dzielimy w zależności od kształtu powierzchni środkowej na:

• tarcze (obciążenie równoległe do powierzchni środkowej).

• tarczownice

• płyty (obciążenie prostopadłe do powierzchni środkowej

• powłoki

Jeśli rozkład naprężeń wzdłuż grubości jest jednorodny (nie zależy od Z) to mamy do czynienia ze stanem tarczowym lub stanem błonowym ( w powłokach bezmomentowych)

Ustroje dzielimy taż ze względu na stan naprężeń:

1. bezmomentowe (rozkład naprężeń wzdłuż grubości jest jednorodny)

• płyty bezmomentowe (tarcze)

- powłoki bezmomentowe (membrana, wyłącznie rozciąganie)

2. ustrój powierzchniowy zginany

Stan bezmometowy jest najkorzystniejszy z punktu widzenia projektowania optymalnych konstrukcji, dąży się do jego realizacji poprzez odpowiednie kształtowanie konstrukcji i jej podparcia oraz sposobu przykładania obciążeń zewnętrznych. Ale problemem jest zabezpieczenie ustroju powierzchniowego przed utratą stateczności, tzw. przed gwałtownym przejściem do stanu giętnego.

Założenia liniowej teorii dzwigarów powierzchniowych

Dla uproszczenia rozwiązań przyjęto założenia zwane hipotezami Kirchhoffa-Love'a oraz kilka dalszych założeń:

1. Hipoteza geometryczna (kinematyczna) -Odcinek prostoliniowy ,prostopadły do nieodkształcalnej powierzchni środkowej pozostaje prostoliniowy, niewydłużalny i prostopadły do powierzchni odkształconej.

2. Hipoteza naprężeniowa - Naprężenie
   jest tak małe w porównaniu z pozostałymi składowymi tensora naprężeń w szczególności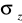
   <<
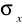
   i
   <<
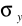
   że można je pominąć w związkach fizycznych, tzn.
   (
   ,
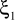
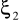
   ,z)
   0

1. Obowiązuje zasada zesztywnienia tzn. przemieszczenia są na tyle małe, że rozwiązania można odnosić do ustroju nieodkształcalnego. Oznacza to, że obowiązują liniowe związki Couchy'ego między przemieszczeniami i odkształceniami.

2. Materiał jest liniowo sprężysty, tj. obowiązuje prawo Hocke'a wyrażające liniowy związek między tensorami naprężeń i odkształceń.

Powyższe założenia prowadzą do pewnych sprzeczności. Dlatego zawęża się je do:

1. ustrój powierzchniowy jest jednorodny o stałej grubości h(
   ,
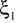
   )=const

2. materiał jest izotropowy o stałych materiałowych E,
   

3. obciążenia przyłożone tylko statycznie

4. pomijamy wpływ temperatury

Tarcze i płyty prostokątne we współrzędnych kartezjańskich

Wielkości uogólnione i siły między nimi.

Uogólnione odkształcenia

Siły przekrojowe

dla stanu tarczowego

Dla stanu giętnego

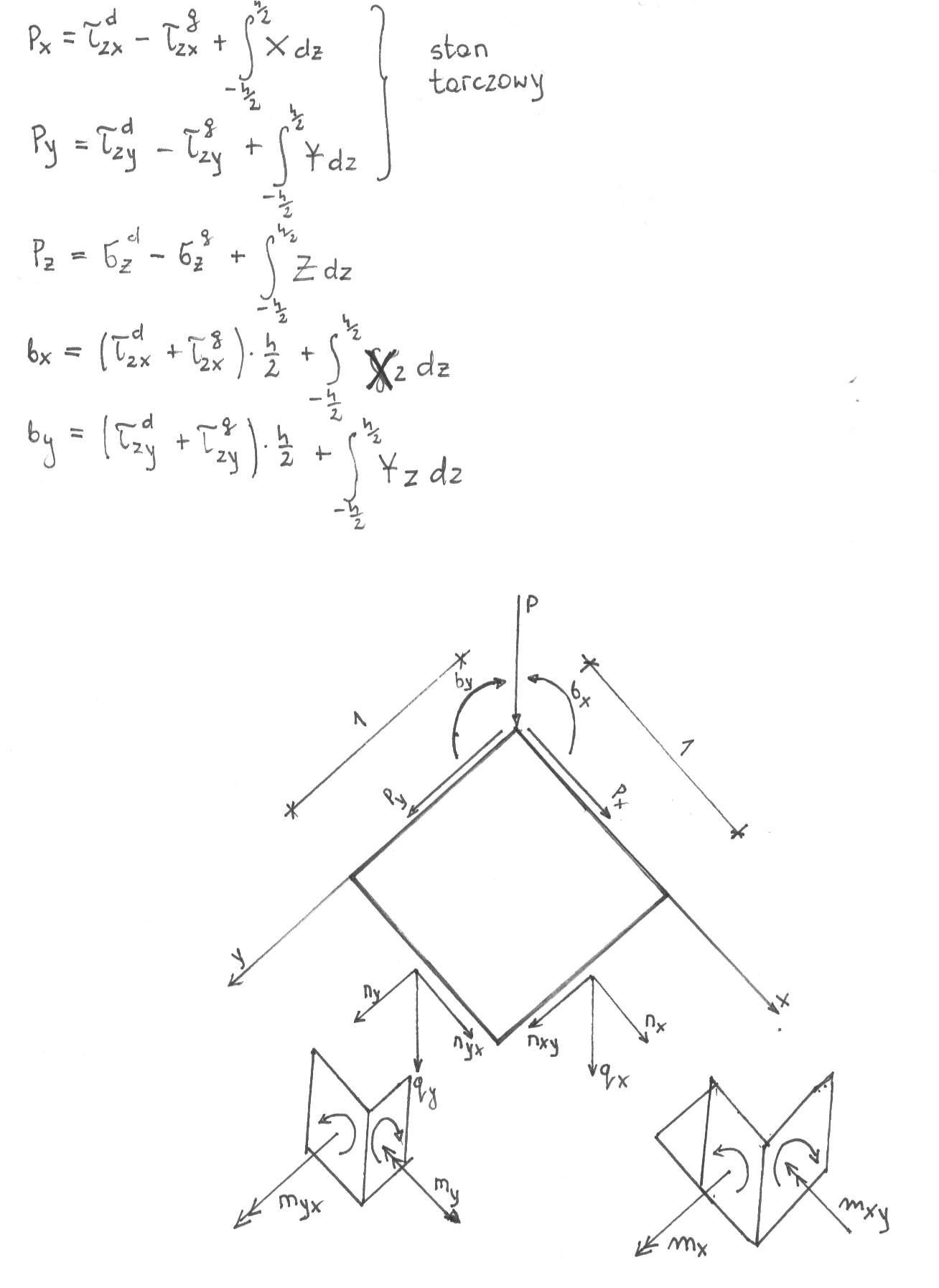
Obciążenia powierzchniowe

Równania fizyczne - wyrażają związki między uogólninymi naprężenimi a uogólninymi odkształceniami.

Płyty kołowe i pierścieniowe

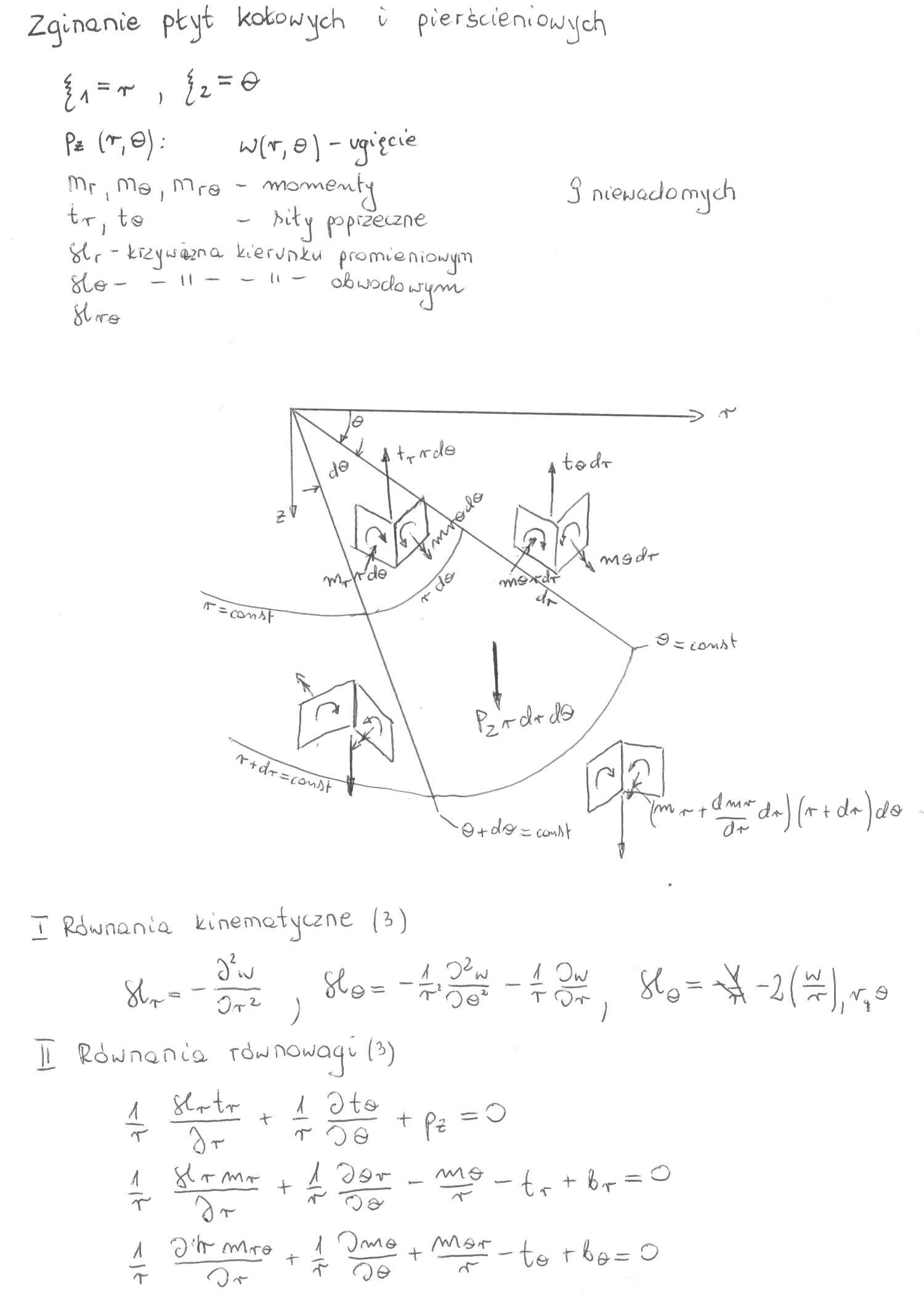
Powłoki w stanie membranowym i giętnym

Powłoki w stanie membranowy i giętnym

Powłoki bezmomentowe stanowią najkorzystniejszy rodzaj powłok ze względów wytrzymałościowych. Przy braku efektów giętnych mamy do czynienia z jednakowym stanem naprężeń wzdłuż grubości powłoki.

Stan bezmomentowy jest możliwy do zrealizowania gdy są spełnione założenia:

1. Powierzchnia środkowa jest gładka bez załomów

2. Obciążenie powierzchniowe jest ciągłe i gładkie a siły brzegowe działają stycznie do powierzchni środkowej.

3. Warunki brzegowe nie krępują przemieszczenia normalnego do powierzchni środkowej `w ` oraz kąta obrotu normalnej.

Osiowo symetryczny stan bezmomentowy

---