Magazynowanie i transport ropy

Temat: Zaprojektować odcinek rurociągu dalekiego zasięgu

spełniającego postawione wymagania.

Adrian Banaś

WWNiG, GiG III rok

Gr.1

niestacjonarne

Projekt zawiera:

1. Wytyczne trasy rurociągu dalekiego zasięgu wraz z opisem.
2. Określenie minimalnej średnicy wewnętrznej rurociągu przy zadanej przepustowości.
3. Dobór gatunku stali rur przewodowych.
4. Określenie naprężenia w rurze rurociągu spowodowane ciśnienie wewnętrznym

tłoczonego medium.

5. Określenie minimalnej grubości ścianki rurociągu metodą stanów granicznych.
6. Obliczenie spadku ciśnienia w rurociągu (przepływ izotermiczny).
7. Określenie naprężenia w rurze rurociągu wywołane ciśnieniem zewnętrznym,

wyznaczenie maks. dopuszczalnej głębokości posadowienia rurociągu.

Założenia projektu:

Do rozważań wytrzymałościowych i hydraulicznych założymy, że projektowany odcinek jest:

- prostoliniowy;

- poziomy (początek i koniec znajdują się na tej samej wysokości);

- jednakowej średnicy i grubości;

- zamontowana armatura, zmiany kierunku itp. powodują zaniedbywalne opory ruchu;

- ulokowany w gruncie o jednakowych właściwościach (także współczynniki przewodzenia
ciepła);

- ulokowany w gruncie o jednakowej temperaturze wzdłuż całej trasy.

Dane projektowe:

Numer projektowy: n=2

Gęstość właściwa ropy naftowej w temp. 30

o

C: 𝜌

𝑟

= 820 [𝑘𝑔/𝑚

3

]

Współczynnik lepkości kinematycznej w temp. 30

o

C: 𝑣

𝑟

= 5,1 ∙ 10

−5

[

𝑚

2

𝑠

]

Długość rurociągu: L=20 km

Wydatek masowy przetłaczanej ropy naftowej: 𝑀 = 2000 [

𝑡

𝑑𝑜𝑏𝑎

] = 23,15 [

𝑘𝑔

𝑠

]

Maksymalna prędkość przepływu ropy przez rurociąg: v=0,9 [m/s]

Ciśnienie wewnątrz rurociągu (ciśnienie tłoczenia ropy): P=3,3 [MPa]

Współczynnik warunków pracy rurociągu: m=0,8

Współczynnik parametrów wytrzymałościowych rurociągu: 𝛾

𝑚

= 1,13

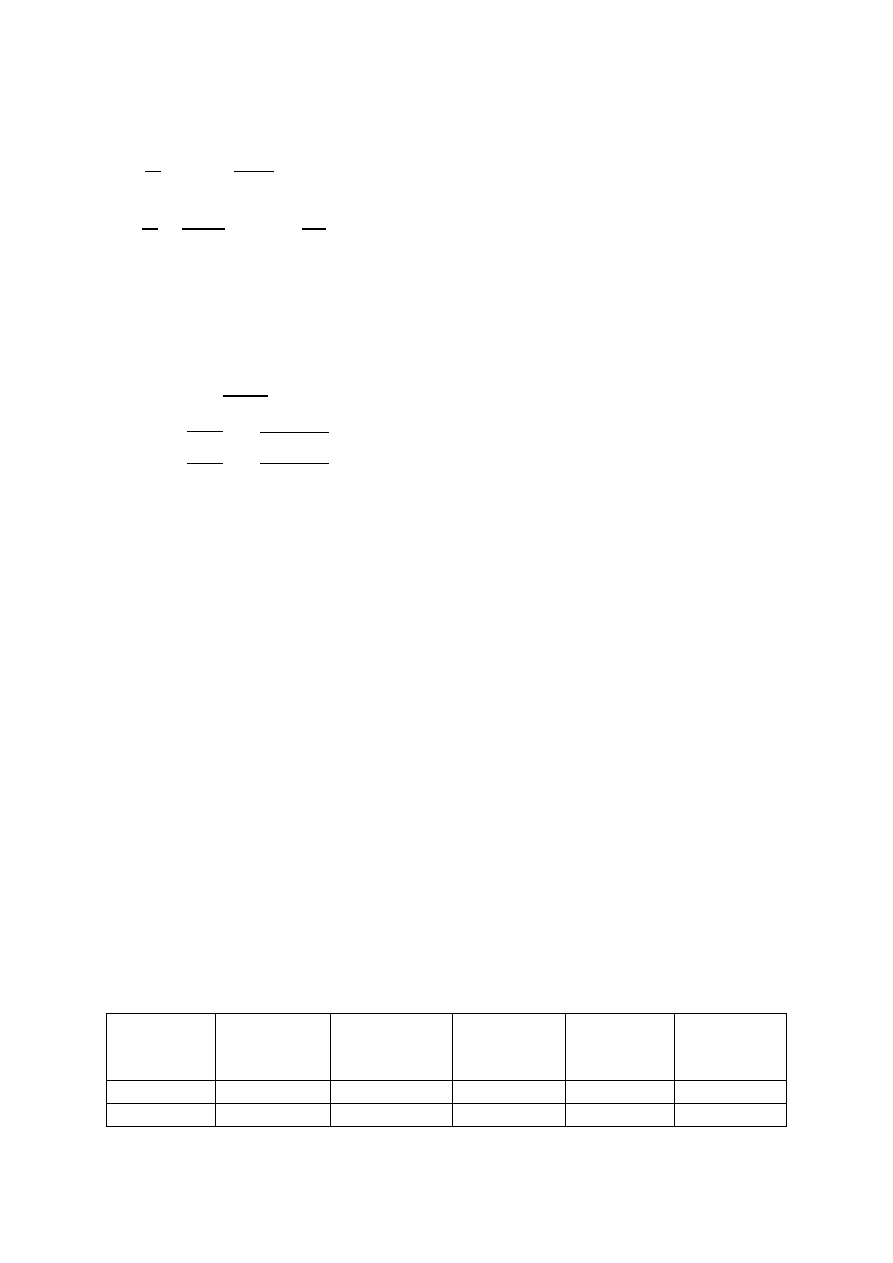
Współczynnik konsekwencji zniszczenia rurociągu: 𝛾

𝑛

= 1,03

Współczynnik obciążenia ciśnieniem wewnętrznym: 𝛾

𝑓

= 1,01

Współczynnik wytrzymałości spoiny w stosunku do obliczeniowej wytrzymałości
materiałowej: 𝛼

𝑠𝑝

= 0,9

Współczynnik korekcyjny: η=0,95

Współczynnik uwzględniający różnicę pomiędzy granicą odkształceń R

e

i granicą rozerwania

R

m

zależny od kategorii rurociągu: k=0,8

Współczynnik pulsacji: 𝛾

𝑝

= 1,0

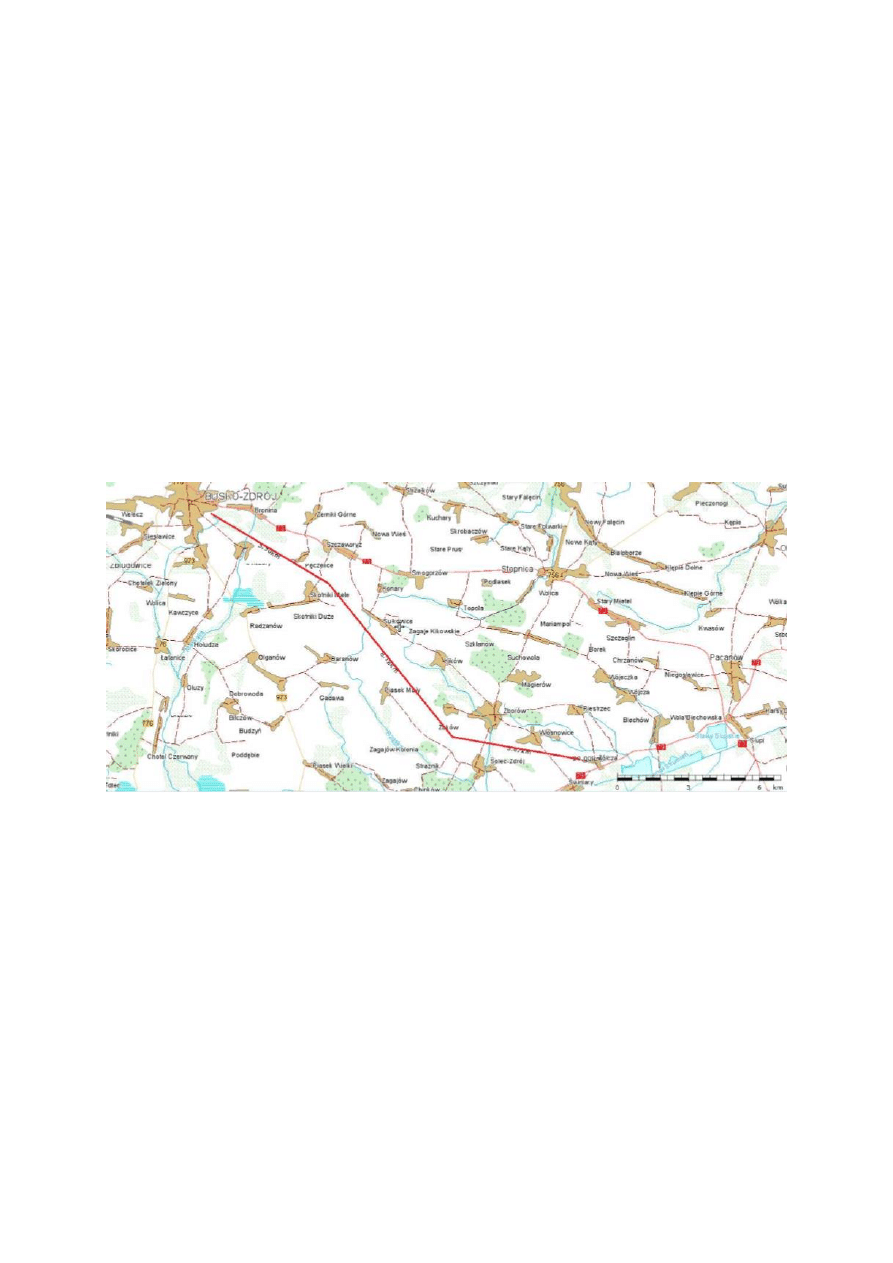
1.Wytyczne trasy rurociągu dalekiego zasięgu wraz z opisem.

Projektowany rurociąg ma przebiegać od miejscowości Busko- Zdrój do miejscowości Żółcza.
Łączna długość rurociągu to 20km. Trasa rurociągu składa się z prostoliniowych odcinków, bez
charakterystycznych przegięć. Długość pierwszego odcinka rurociągu to 5,90km, jest to
odległość od Buska- Zdroju do miejscowości o nazwie Skotniki Małe. Kolejny odcinek ma
długość 8,18km, jego koniec znajduje się na południe od miejscowości Żuków, ostatni odcinek
rurociągu ma długość 5,92km.Na trasie rurociągu nie napotykamy jakiś szczególnych
przeszkód, brak na niej lasów, gór. Jedyną przeszkodą jaką musimy pokonać to trzy niewielkie
cieki wodne, o bardzo małej szerokości oraz kilka dróg lokalnych. Trasa rurociągu została
wytyczona tak aby na drodze rurociągu nie napotkać chroniony obiektów przyrody, ponieważ
czego niestety nie widać na rysunku zamieszczonym poniżej na północ od miejscowości
Owczary znajduje się Rezerwat Owczary oraz południowy-wschód od miejscowości Skotniki
Małe, mamy Rezerwat Kapturowa Góra. Wzdłuż całej trasy rurociągu występują pola uprawne,
co wiąże się z tym że przed przystąpieniem do realizacji projektu niezbędne będzie uzyskanie
zgód o właścicieli tych terenów na wykonywanie prac na ich posiadłościach

2. Określenie minimalnej średnicy wewnętrznej rurociągu.

𝑀 =

𝑚

𝑡

= 2000 [

𝑡

𝑑𝑜𝑏𝑎

]

𝑄 =

𝑀

𝜌

=

23,15

820

= 0,028 [

𝑚

3

𝑠

]

Określenie minimalnej średnicy wewnętrznej rurociągu na podstawie minimalnego
wymaganego wydatku tłoczenia ropy naftowej oraz maksymalnej prędkości przepływu. Po
przekształceniu wzoru na wydatek objętościowy przetłaczanej ropy otrzymamy wyrażenie na
minimalną średnicę wewnętrzną rurociągu

𝑄 = 𝑣 ∙ 𝐴 = 𝑣 ∙

𝜋 ∙ 𝑑

𝑤

2

4

=

𝑑

𝑤

𝑚𝑖𝑛

= √

4 ∙ 𝑄

𝜋 ∙ 𝑣

= √

4 ∙ 0,028

3,14 ∙ 0,9

= 0,199 [𝑚]

Gdzie:

M – masowy wydatek przepływu medium (ropy naftowej);

m – masa przepływającego medium (ropy naftowej);

t – czas przepływu masy m tłoczonego medium (ropy naftowej);

𝜌 – gęstość właściwa tłoczonego medium (ropy naftowej);

Q – wydatek objętościowy przepływu medium (ropy naftowej);

A – pole wewnętrznego przekroju poprzecznego rurociągu;

v – maksymalna prędkość przepływu medium przez rurociąg;

d

w

– średnica wewnętrzna rurociągu;

𝑑

𝑤

𝑚𝑖𝑛

– poszukiwana minimalna średnica wewnętrzna rurociągu

.

3. Dobór gatunku stali i rur przewodowych.

Do wykonania rurociągu zostały wybrane rury do mediów o parametrach:

Gatunek

stali

Górna

granica

plastyczności

Wytrzymałość

na

rozciąganie

Średnica

wewnętrzna

Grubość

ścianki

Średnica

zewnętrzna

R

e

[MPa]

R

m

[MPa]

d

w

[m]

g

s

[m]

d

z

[m]

L290NB

290

415

0,35

0,0125

0,375

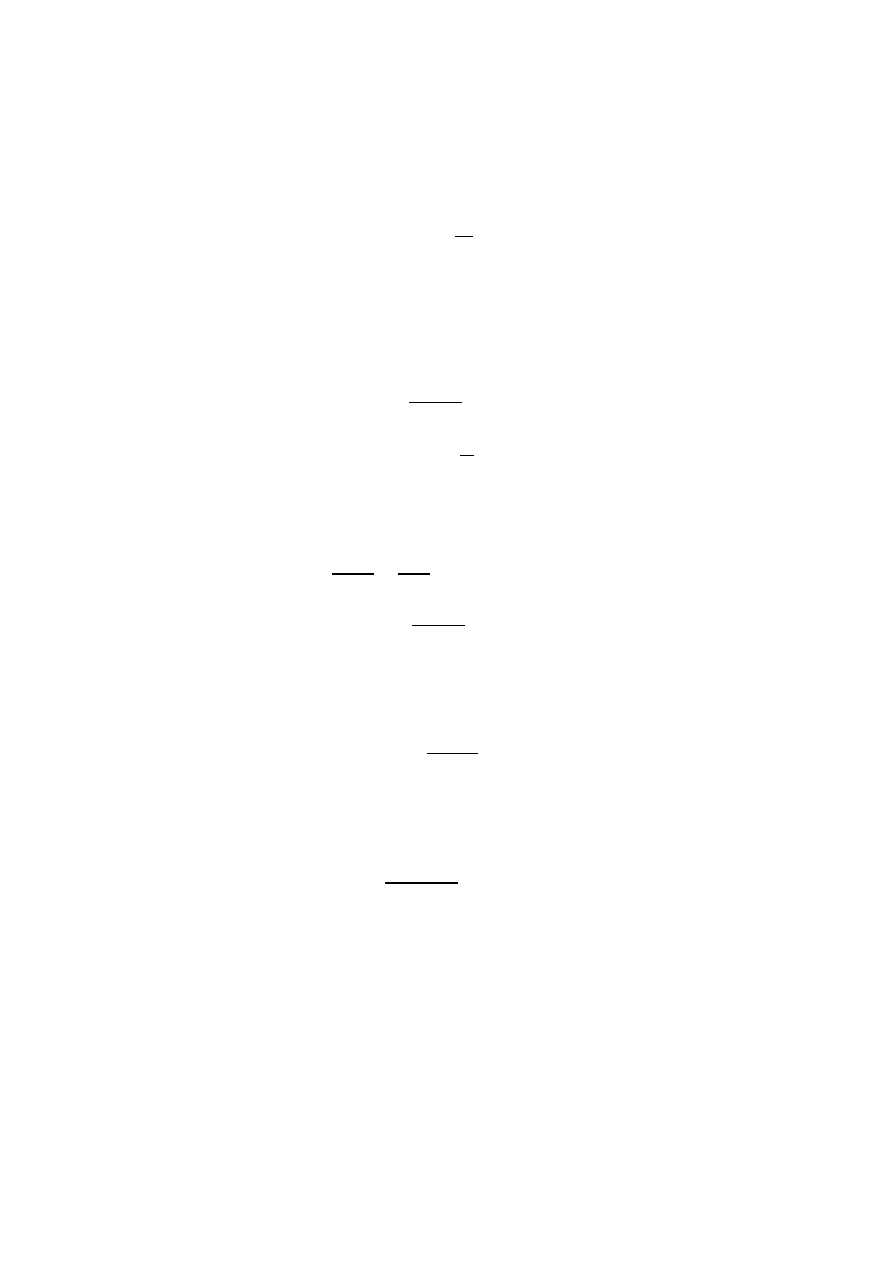
4. Określenie naprężenia w rurze rurociągu spowodowane ciśnienie
wewnętrznym tłoczonego medium.

Obliczenie parametrów 𝛽 𝑖 𝛽

𝑟

:

𝛽 =

𝑟

𝑧

𝑟

𝑤

Gdzie:

r

z

– promień zewnętrzny rurociągu [m];

r

w

– promień wewnętrzny rurociągu [m].

𝛽 =

0,1875

0,175

= 1,07

𝛽

𝑟

=

𝑟

𝑧

𝑟

Gdzie:

r

z

– promień zewnętrzny rurociągu [m];

r – odległość pkt. od osi rury r=

𝑑

𝑤.𝑚𝑖𝑛

2

=

0,282

2

= 0,141[𝑚]

𝛽

𝑟

=

0,1875

0,141

= 1,33

Obliczenie naprężeń osiowych:

𝜎

𝑠

= 𝑃 ∙

1

𝛽

2

− 1

[𝑀𝑃𝑎]

Gdzie:

P – nominalne ciśnienie wewnątrz rurociągu [MPa].

𝜎

𝑠

= 6,7 ∙

1

1,07

2

− 1

= 46,238[𝑀𝑃𝑎]

Obliczenie naprężeń promieniowych w rurociągu na ściance wewnętrznej rury:

𝜎

𝑟.𝑤

= −𝑃[𝑀𝑃𝑎]

Gdzie:

P – nominalne ciśnienie wewnątrz rurociągu

𝜎

𝑟.𝑤

= −6,7[𝑀𝑃𝑎]

Obliczenie naprężeń promieniowych w rurociągu na ściance zewnętrznej rury:

𝜎

𝑟.𝑧

= 0

Obliczenie naprężeń obwodowych w rurociągu na ściance wewnętrznej rury:

𝜎

𝑜.𝑤

= 𝑃 + 𝑃 ∙

𝑑

𝑤

2

2 ∙ 𝑔

𝑠

∙ (𝑑

𝑤

+ 𝑔

𝑠

)

[𝑀𝑃𝑎]

Gdzie:

P – nominalne ciśnienie wewnątrz rurociągu [MPa];

d

w

– wewnętrzna średnica rur [m];

g

s

– grubość ścianki [m].

𝜎

𝑜.𝑤

= 6,7 + 6,7 ∙

0,350

2

2 ∙ 0,0125 ∙ (0,350 + 0,0125)

= 97,266[𝑀𝑃𝑎]

Obliczenie naprężen obwodowych w rurociągu na ściance zewnętrznej rury:

𝜎

𝑜.𝑧

= 𝑃 ∙

𝑑

𝑤

2

2 ∙ 𝑔

𝑠

∙ (𝑑

𝑤

+ 𝑔

𝑠

)

[𝑀𝑃𝑎]

𝜎

𝑜.𝑤

= 6,7 ∙

0,350

2

2 ∙ 0,0125 ∙ (0,350 + 0,0125)

= 90,566[𝑀𝑃𝑎]

Obliczenie naprężeń osiowych w rurociągu:

𝜎

𝑠

= 𝑃 ∙

𝑑

𝑤

2

4 ∙ 𝑔

𝑠

∙ (𝑑

𝑤

+ 𝑔

𝑠

)

[𝑀𝑃𝑎]

𝜎

𝑠

= 6,7 ∙

0,350

2

4 ∙ 0,0125 ∙ (0,350 + 0,0125)

= 45,283[𝑀𝑃𝑎]

Obliczenie naprężeń zredukowanych w rurociągu na ściance zewnętrznej rury:

𝜎

𝑧𝑟,𝑧

= √3 ∙ 𝑃 ∙

𝑑

𝑤

2

4 ∙ 𝑔

𝑠

∙ (𝑑

𝑤

+ 𝑔

𝑠

)

[𝑀𝑃𝑎]

𝜎

𝑧𝑟,𝑧

= √3 ∙ 6,7 ∙

0,350

2

4 ∙ 0,0125 ∙ (0,350 + 0,0125)

= 78,432[𝑀𝑃𝑎]

Po przeanalizowaniu obliczeń powyżej widzimy że naprężenie spowodowane przepływającą
ropą są mniejsze od parametrów wytrzymałościowych dobranej rury. Na tej podstawie
można stwierdzić że do projektu została dobrana rura o odpowiednich parametrach.

5. Określenie minimalnej grubości ścianki rurociągu metodą stanów
granicznych.

Obliczenie zmodyfikowanej wytrzymałości na rozciąganie.

𝑓

𝑑

=

𝑅

𝑚

∙ 𝑚

𝛾

𝑚

∙ 𝛾

𝑛

Gdzie:

R

m

– minimalna wytrzymałość stali lub połączeń spawanych na rozciąganie,

M – współczynnik warunków pracy rurociągu – zwykle m = 0,6-0,9,

𝛾

𝑚

– współczynnik parametrów wytrzymałościowych rurociągu – zwykle dla rurociągów

naziemnych 𝛾

𝑚

= 1,1-1,2, dla rurociągów podziemnych 𝛾

𝑚

= 1,34-1,55,

𝛾

𝑛

– współczynnik konsekwencji zniszczenia rurociągu – zwykle 𝛾

𝑛

= 1-1,1

𝑓

𝑑

=

415 ∙ 0,8

1,13 ∙ 1,03

= 285,248[𝑀𝑃𝑎]

Obliczenie minimalnej grubości ścianki metodą stanów granicznych:

I stan graniczny

- Jednoosiowy stan naprężeń

𝑔

𝑠

=

𝛾

𝑓

∙ 𝑝 ∙ 𝑑

𝑧

2 ∙ (𝑓

𝑑

∙ 𝛼

𝑠𝑝

∙ 𝛾

𝑝

+ 𝛾

𝑓

∙ 𝑝)

gdzie

𝛾

𝑓

– współczynnik obciążenia ciśnieniem wewnętrznym – zwykle przyjmuje się 𝛾

𝑓

= 1-1,15,

p – nominalnie ciśnienie wewnątrz rurociągu [-],

d

z

– zewnętrzna średnica rury [m],

f

d

– zmodyfikowana wytrzymałość na rozciąganie [MPa],

𝛼

𝑠𝑝

– współczynnik wytrzymałości spoiny w stosunku do obliczeniowej wytrzymałości

materiałowej,

𝛾

𝑝

– współczynnik pulsacji,

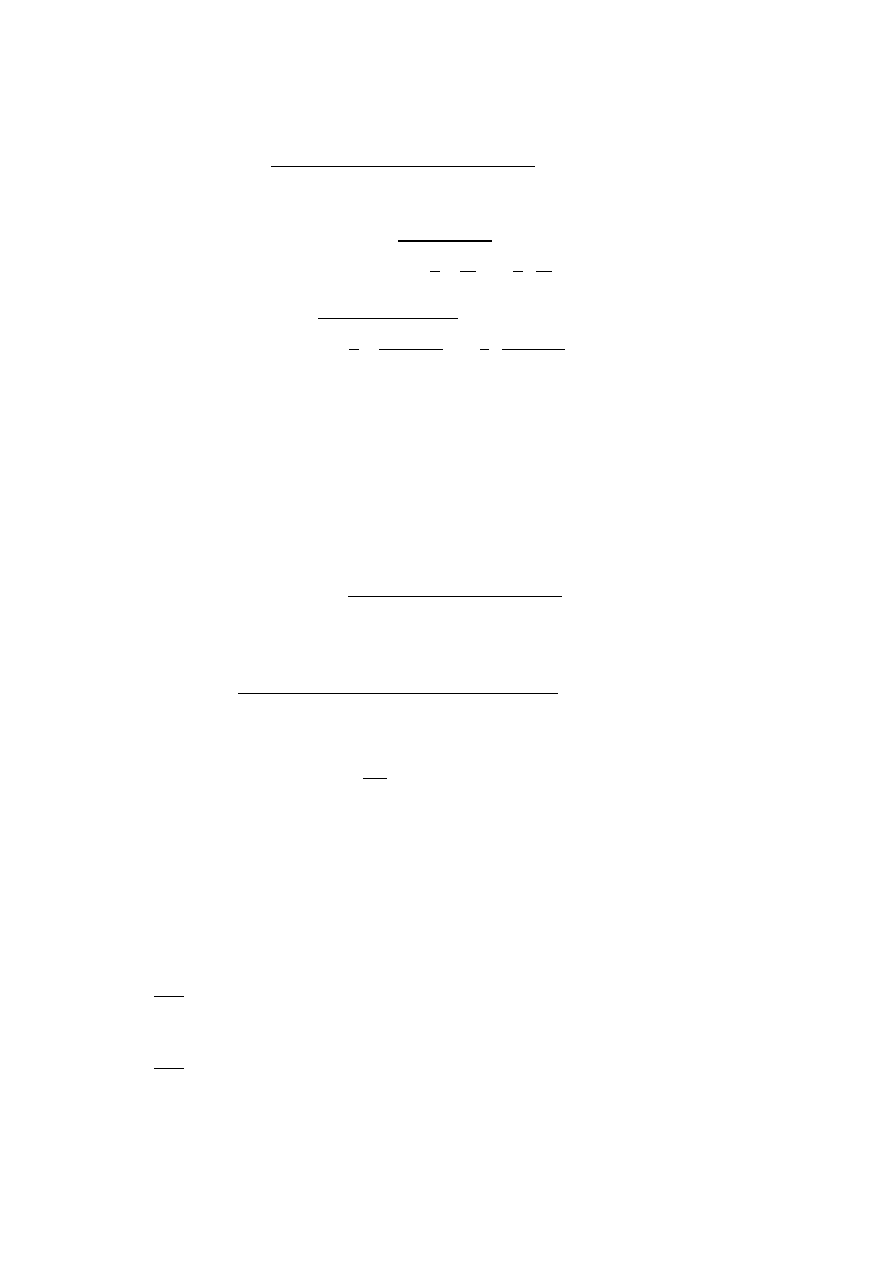
𝛾

𝑓

– współczynnik obciążenia ciśnieniem wewnętrznym.

𝑔

𝑠1

=

1,01 ∙ 6.7 ∙ 0,375

2 ∙ (285,248 ∙ 0,9 ∙ 1,0 + 1,01 ∙ 6,7)

= 4,82 ∙ 10

−3

[𝑚]

-Dwuosiowy stan naprężeń:



1

= √1 −

3
4

∙ (

𝜎

𝑠

𝑓

𝑑

)

2

−

1
2

∙

𝜎

𝑠

𝑓

𝑑



1

= √1 −

3
4

∙ (

46,238

285,248

)

2

−

1
2

∙

46,238

285,248

= 0,909

Gdzie:



1

- parametr uwzględniający dwuosiowy stan naprężeń,

𝜎

𝑠

- naprężenie osiowe w rurociągu [MPa],

𝑓

𝑑

– zmodyfikowana wytrzymałość na rozciąganie [MPa].

𝑔

𝑠2

=

𝛾

𝑓

∙ 𝑝 ∙ 𝑑

𝑧

2 ∙ (



1

∙ 𝑓

𝑑

∙ 𝛼

𝑠𝑝

∙ 𝛾

𝑝

+ 𝛾

𝑓

∙ 𝑝)

[𝑚]

𝑔

𝑠2

=

1,01 ∙ 6.7 ∙ 0,375

2 ∙ (0,909 ∙ 285,248 ∙ 0,9 ∙ 1,0 + 1,01 ∙ 6,7)

= 5,436 ∙ 10

−3

[𝑚]

Liniowa prędkość korozji: 0,05 ÷ 1

𝑚𝑚

𝑟𝑜𝑘

Po 50 latach eksploatacji rurociągu 5mm korozji.

𝑔

𝑠

= 5,436 ∙ 10

−3

+ 5 ∙ 10

−3

= 10,436 ∙ 10

−3

[𝑚] – wartość ta jest mniejsza od wybranego,

więc dobrze dobrano grubość ścianki rurociągu.

Ponadto przy doborze grubości ścianki należy spełnić dodatkowe warunki techniczne:

𝑔

𝑠

≥ {

1

140

∙ 𝑑

𝑧

4𝑚𝑚

𝑔

𝑠

≥ {

1

140

∙ 0,375 = 2,6[𝑚𝑚]

4𝑚𝑚

- Jednoosiowy układ naprężeń

Warunek: 𝜎

𝑜

≤ 𝑓

𝑑

𝜎

𝑜

= 𝛾

𝑓

∙ 𝑝 ∙

(𝑑

𝑧

− 2 ∙ 𝑔

𝑠

)

2 ∙ 𝑔

𝑠

[𝑀𝑃𝑎]

𝜎

𝑜

= 1,01 ∙ 6,7 ∙

(0,375 − 2 ∙ 0,0125)

2 ∙ 0,0125

= 94,738[𝑀𝑃𝑎]

Sprawdzenie warunku:

94,738 [𝑀𝑃𝑎] ≤ 285,248 [𝑀𝑃𝑎] − 𝑤𝑎𝑟𝑢𝑛𝑒𝑘 𝑧𝑜𝑠𝑡𝑎ł 𝑠𝑝𝑒ł𝑛𝑖𝑜𝑛𝑦

- Dwuosiowy układ naprężeń

Warunek: 𝜎

𝑜

≤



1

∙ 𝑓

𝑑

𝜎

𝑠

= 1,01 ∙ 6,7 ∙

(0,375 − 2 ∙ 0,0125)

4 ∙ 0,0125

= 47,369[𝑀𝑃𝑎]

Sprawdzenie warunku:



1

∙ 𝑓

𝑑

= 0,909 ∙ 285,248 = 234,747[𝑀𝑃𝑎]

47,369[𝑀𝑃𝑎] ≤ 234,747[𝑀𝑃𝑎] − 𝑤𝑎𝑟𝑢𝑛𝑒𝑘 𝑧𝑜𝑠𝑡𝑎ł 𝑠𝑝𝑒ł𝑛𝑖𝑜𝑛𝑦

Warunek:

𝑅

𝑒

𝑅

𝑚

≥ 0,75

Sprawdzenie warunku:

290
415

= 0,698 − 𝑤𝑎𝑟𝑢𝑛𝑒𝑘 𝑛𝑖𝑒 𝑧𝑜𝑠𝑡𝑎ł 𝑠𝑝𝑒ł𝑛𝑖𝑜𝑛𝑦, 𝑛𝑎𝑙𝑒ż𝑦 𝑠𝑝𝑟𝑎𝑤𝑑𝑧𝑖ć 𝐼𝐼 𝑠𝑡𝑎𝑛 𝑔𝑟𝑎𝑛𝑖𝑐𝑧𝑛𝑦

II stan graniczny

- Jednoosiowy stan naprężeń

𝑔

𝑠1

=

𝛾

𝑓

∙ 𝑃 ∙ 𝑑

𝑧

2 ∙ (

κ

η ∙ 𝑓

𝑑

∙ 𝛼

𝑠𝑝

∙ 𝛾

𝑝

+ 𝛾

𝑓

∙ 𝑃)

[𝑚]

𝑔

𝑠1

=

1,01 ∙ 6,7 ∙ 0,375

2 ∙ (

0,8

0,95

∙ 285,248 ∙ 0,9 ∙ 1,0 + 1,01 ∙ 6,7)

= 5,69 ∙ 10

−3

[𝑚]

𝛾

𝑓

- współczynnik obciążenia ciśnieniem wewnętrznym,

P – nominalne ciśnienie wewnątrz rurociągu [MPa],

κ - współczynnik uwzględniający różnicę pomiędzy granicą odkształceń R

e

i granicą rozerwania R

m

,

η - współczynnik korekcyjny,

d

z

– zewnętrzna średnica rury,

f

d

- zmodyfikowana wytrzymałość na rozciąganie [MPa],

𝛼

𝑠𝑝

- współczynnik wytrzymałości spoiny w stosunku do obliczeniowej wytrzymałości

materiałowej,

𝛾

𝑝

- współczynnik pulsacji,

𝛾

𝑓

– współczynnik obciążenia ciśnieniem wewnętrznym.

- Dwuosiowy stan naprężeń



2

= √1 −

3
4

∙ (

𝜎

𝑠

κ

η ∙ 𝑓

𝑑

)

2

−

1
2

∙

𝜎

𝑠

κ

η ∙ 𝑓

𝑑



2

= √1 −

3
4

∙ (

46,238

0,8

0,95

∙ 285,248

)

2

−

1
2

∙

46,238

0,8

0,95

∙ 285,248

= 0,889

𝑔

𝑠2

=

𝛾

𝑓

∙ 𝑃 ∙ 𝑑

𝑧

2 ∙ (



2

∙

κ

η ∙ 𝑓

𝑑

∙ 𝛼

𝑠𝑝

∙ 𝛾

𝑝

+ 𝛾

𝑓

∙ 𝑃)

=

1,01 ∙ 6,7 ∙ 0,375

2 ∙ (0,889 ∙

0,8

0,95

∙ 285,248 ∙ 0,9 ∙ 1,0 + 1,01 ∙ 6,7

= 6,38 ∙ 10

−3

[𝑚]

Po uwzględnieniu poprawki na korozję: 𝑔

𝑠

= 6,38 ∙ 10

−3

+ 5 ∙ 10

−3

= 11,38 ∙ 10

−3

- Jednoosiowy układ naprężeń

Warunek: 𝜎

𝑜

≤

κ

η

∙ 𝑓

𝑑

𝜎

𝑜

= 𝛾

𝑓

∙ 𝑝 ∙

(𝑑

𝑧

− 2 ∙ 𝑔

𝑠

)

2 ∙ 𝑔

𝑠

[𝑀𝑃𝑎]

𝜎

𝑜

= 1,01 ∙ 6,7 ∙

(0,375 − 2 ∙ 0,0125)

2 ∙ 0,0125

= 94,738[𝑀𝑃𝑎]

Sprawdzenie warunku:

κ

η

∙ 𝑓

𝑑

=

0,8

0,95

∙ 258,248 = 217,472[𝑀𝑃𝑎]

94,738 [𝑀𝑃𝑎] ≤ 217,472 [𝑀𝑃𝑎] − 𝑤𝑎𝑟𝑢𝑛𝑒𝑘 𝑧𝑜𝑠𝑡𝑎ł 𝑠𝑝𝑒ł𝑛𝑖𝑜𝑛𝑦

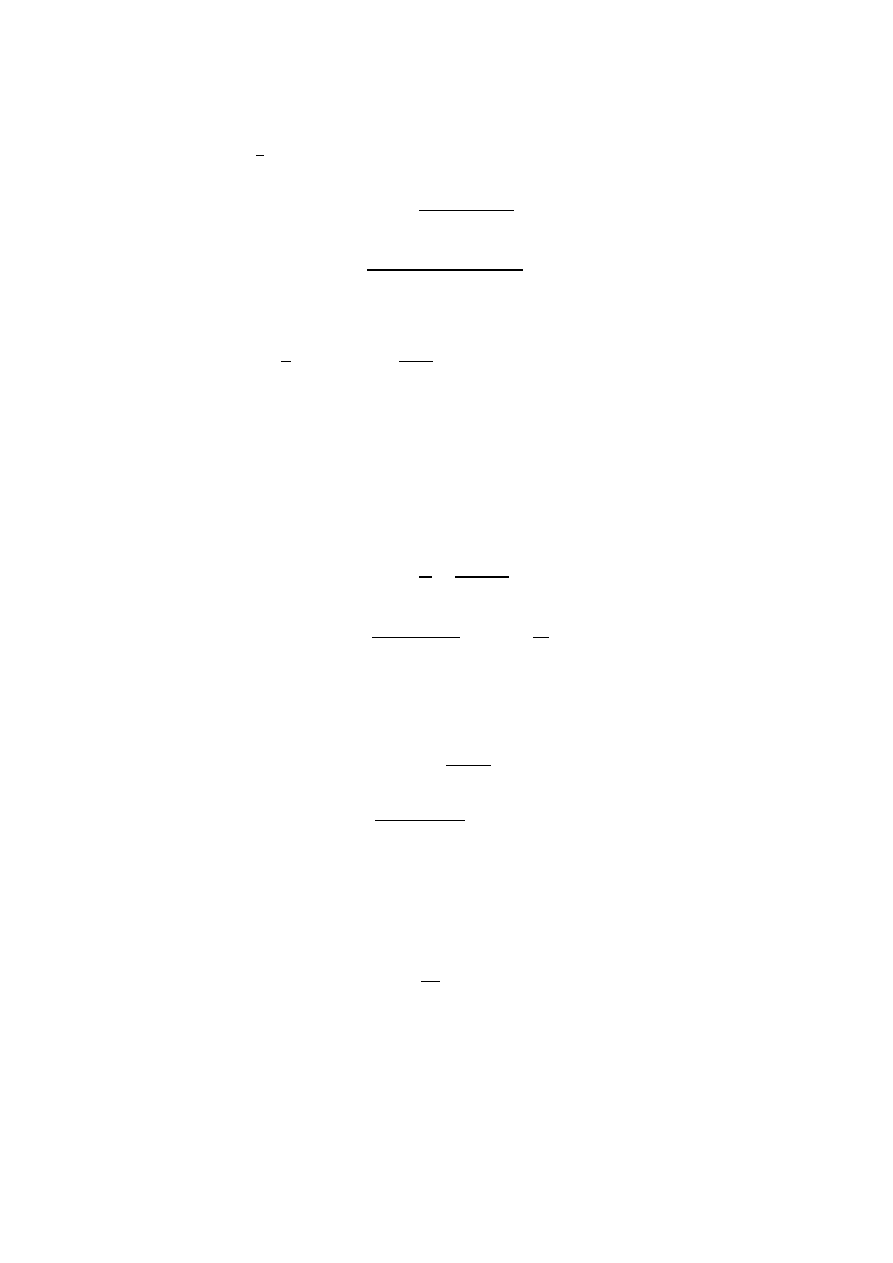
- Dwuosiowy układ naprężeń

Warunek: 𝜎

𝑜

≤



2

∙

κ

η

∙ 𝑓

𝑑

𝜎

𝑜

= 𝛾

𝑓

∙ 𝑝 ∙

(𝑑

𝑧

− 2 ∙ 𝑔

𝑠

)

4 ∙ 𝑔

𝑠

[𝑀𝑃𝑎]

𝜎

𝑜

= 1,01 ∙ 6,7 ∙

(0,375 − 2 ∙ 0,0125)

4 ∙ 0,0125

= 47,369[𝑀𝑃𝑎]

Sprawdzenie warunku:



2

∙

κ

η

∙ 𝑓

𝑑

= 0,889 ∙

0,8

0,95

∙ 258,248 = 193,333[𝑀𝑃𝑎]

47,369 [𝑀𝑃𝑎] ≤ 193,333 [𝑀𝑃𝑎] − 𝑤𝑎𝑟𝑢𝑛𝑒𝑘 𝑧𝑜𝑠𝑡𝑎ł 𝑠𝑝𝑒ł𝑛𝑖𝑜𝑛𝑦

6. Obliczenie spadku ciśnienia w rurociągu.

Obliczenie średniej liniowej prędkości przepływu ropy:

𝑢 =

𝑄

𝐴

=

4 ∙ 𝑄

𝜋 ∙ 𝑑

𝑤

2

𝑢 =

4 ∙ 0,028

3,14 ∙ 0,35

2

= 0,291[

𝑚

𝑠

]

Obliczenie Liczby Reynoldsa:

𝑅𝑒 =

𝑢 ∙ 𝑑

𝑤

𝑣

𝑅𝑒 =

0,291 ∙ 0,35

5,1 ∙ 10

−5

= 1997,058

Re = 1997,058 -> przepływ laminarny

Obliczenie współczynnika oporu przepływu:

λ =

64
𝑅𝑒

= 0,032

Obliczenie spadku ciśnienia w rurociągu:

∆𝑝 = 𝑝

1

− 𝑝

2

=

λ ∙

𝑢

2

∙ 𝐿 ∙ 𝜌

𝑟

2 ∙ 𝑑

𝑤

∆𝑝 =

0,032 ∙

0,291

2

∙ 20000 ∙ 820

2 ∙ 0,35

= 0,06349 [𝑀𝑃𝑎]

L – długość odcinka rurociągu

Obliczony spadek ciśnienia jest mniejszy od ciśnienia tłoczenia ropy, dzięki czemu nie będzie

problemów z przetłoczeniem ropy

7.Określenie naprężenia w rurze rurociągu wywołane ciśnieniem
zewnętrznym, wyznaczenie maks. dopuszczalnej głębokości
posadowienia rurociągu.

Obliczenie ciśnienia krytycznego, które powoduje spłaszczenie przekroju rurociągu:

𝑃

𝑘𝑟𝑦𝑡

=

2 ∙ 𝐸

1 − 𝑣

2

∙ (

𝑔

𝑠

𝑑

𝑠𝑟

)

3

[𝑀𝑃𝑎]

Gdzie:

E – moduł Younga dla materiału rury [MPa],

𝑣 – współczynnik Poissona dla stali,

𝑔

𝑠

– grubość ścianki [m],

𝑑

𝑠𝑟

– średnia średnica rury [m].

𝑑

𝑠𝑟

=

𝑑

𝑤

+ 𝑑

𝑧

2

=

0,35 + 0,375

2

= 0,363[𝑚]

𝑃

𝑘𝑟𝑦𝑡

=

2 ∙ 2,1 ∙ 10

5

1 − 0,3

2

∙ (

0,0125

0,363

)

3

= 18,845[𝑀𝑃𝑎]

Obliczenie dopuszczalnego ciśnienia zewnętrznego:

P

z

≤

P

kryt

5

P

kryt

– ciśnienie krytyczne powodujące spłaszczenie rurociągu.

P

z

≤

18,845

5

P

z

≤ 3,769[𝑀𝑃𝑎]

Obliczenie naprężeń pionowych w gruncie:

𝜎

𝑧

= 𝜌

𝑠𝑟

∙ 𝑔 ∙ ℎ

𝑠𝑟

[𝑀𝑃𝑎]

𝜎

𝑧

= 2000 ∙ 9,80665 ∙ 0,5 = 0,0098[𝑀𝑃𝑎]

Gdzie

𝜌

𝑠𝑟

– średnia gęstość właściwa nadkładu [kg/m

3

],

𝑔 – przyspieszenie ziemskie [m/s

2

],

ℎ

𝑠𝑟

– średnia wysokość nadkładu [m].

Obliczenie naprężeń poziomych w gruncie:

𝜎

𝑥

= 𝜎

𝑦

= 𝑘 ∙ 𝜎

𝑧

Gdzie:

k – współczynnik bocznego nacisku,

𝜎

𝑧

– naprężenie pionowe w gruncie [MPa].

𝑘 =

𝑣

1 − 𝑣

=

0,3

1 − 0,3

= 0,429

𝜎

𝑥

= 𝜎

𝑦

= 0,429 ∙ 0,0098 = 0,0042[𝑀𝑃𝑎]

Lp.

d

w

g

s

d

sr

h

sr

𝛔

𝐳

𝛔

𝐱

, 𝛔

𝐲

P

kryt

P

kryt

/5 𝛔

𝐳

OK.?

-

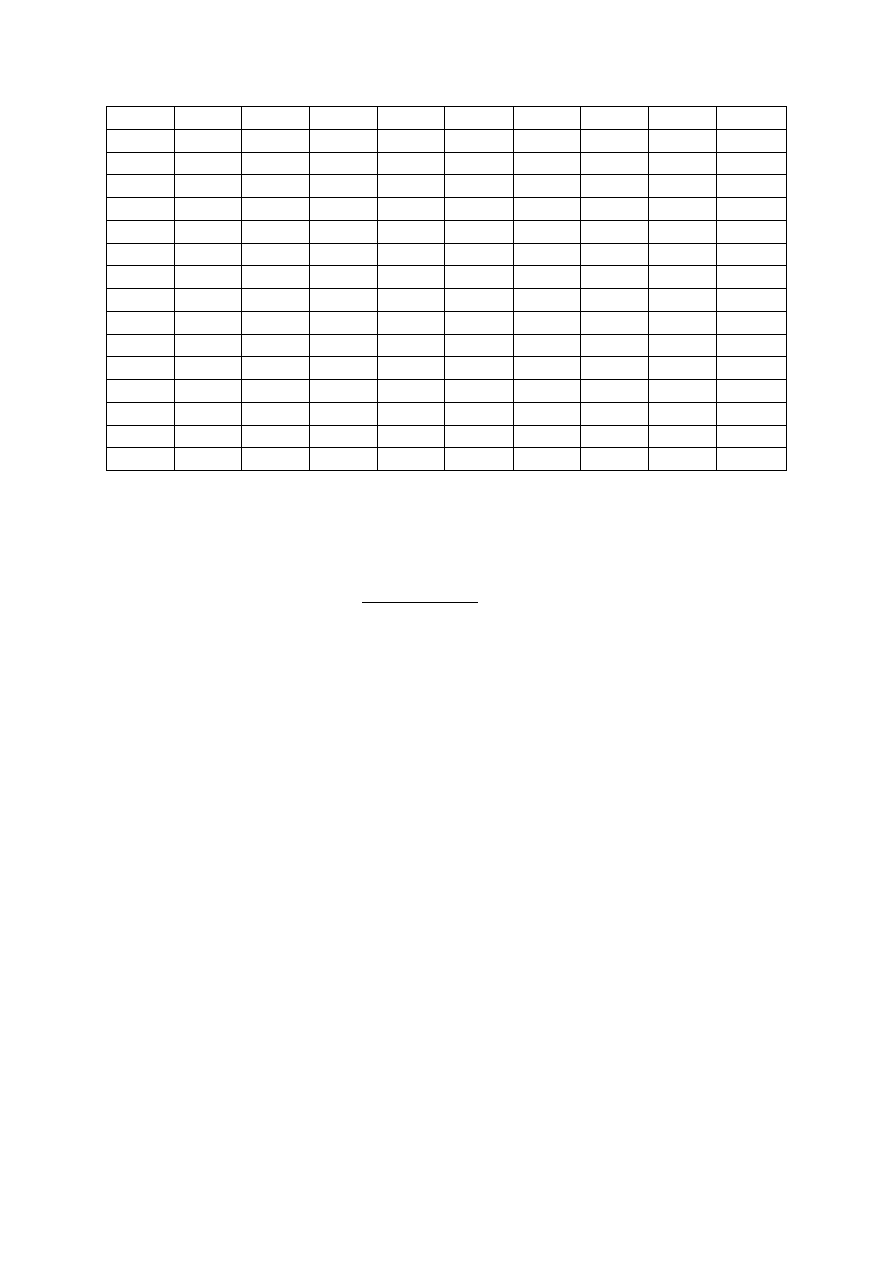
mm

mm

mm

m

MPa

MPa

MPa

MPa

tak/nie

1

350

12,5

363

0,5

0,0098 0,0042 18,845

3,769

tak

2

350

12,5

363

0,8

0,016

0,0067 18,845

3,769

tak

3

350

12,5

363

1,0

0,02

0,0084 18,845

3,769

tak

4

350

12,5

363

1,2

0,024

0,01

18,845

3,769

tak

5

350

12,5

363

1,5

0,029

0,013

18,845

3,769

tak

6

350

12,5

363

2,0

0,039

0,017

18,845

3,769

tak

7

350

12,5

363

3,0

0,059

0,025

18,845

3,769

tak

8

350

12,5

363

5,0

0,098

0,042

18,845

3,769

tak

9

350

12,5

363

8,0

0,157

0,067

18,845

3,769

tak

10

350

12,5

363

10,0

0,196

0,084

18,845

3,769

tak

11

350

12,5

363

20

0,392

0,168

18,845

3,769

tak

12

350

12,5

363

50

0,981

0,42

18,845

3,769

tak

13

350

12,5

363

100

1,961

0,841

18,845

3,769

tak

14

350

12,5

363

200

3,923

1,681

18,845

3,769

nie

15

350

12,5

363

500

9,807

4,203

18,845

3,769

nie

Obliczenie maksymalnej głębokości posadowienia rurociągu bez zmian przekroju:

𝜎

𝑧

= 𝜌

𝑠𝑟

∙ 𝑔 ∙ ℎ

𝑚𝑎𝑥

[𝑀𝑃𝑎]

ℎ

𝑚𝑎𝑥

=

18,845 ∙ 10

6

2000 ∙ 9,80665

= 960,827[𝑚]