1

Dane:

Obliczenia:

Wyniki:

Ciężar zawieszony
na linie wciągarki:

= 19

Prędkość liniowa
podnoszenia
ciężaru:

= 1,1

Średnica

bębna

wciągarki:

= 550

1.

Obliczenia wstępne, dobór silnika

1.1.

Moc na wale wyjściowym

=

∙

1000

=

19000 ∙ 1,1

1000

= 20,9

1.2.

Sprawności poszczególnych układów

•

Przekładnia pasowa:

= 0,95

•

Przekładnia zębata:

= 0,97

•

Układu łożyskowania:

ł

= 0,995

•

Sprzęgła:

= 0,98

•

Sprawność całkowita:

=

∙

∙

ł

∙

= 0,899

1.3.

Moc obliczeniowa silnika elektrycznego

=

= 23,26

1.4.

Maksymalne

i

minimalne

przełożenia

poszczególnych

przekładni

•

Przekładnia pasowa:

"

#$%

= 2

"

#&'

= 5

•

Przekładnia zębata o zębach prostych:

"

#$%

= 2,5

"

#&'

= 4

•

Przekładnia zębata o zębach skośnych

"

#$%

= 2,5

"

#&'

= 4

1.5.

Minimalne i maksymalne przełożenie układu:

"

)#$%

= "

#$%

∙ "

#$%

∙ "

#$%

= 12,5

"

)#&'

= "

#&'

∙ "

#&'

∙ "

#&'

= 80

= 20,9

= 23,26

2

Parametry

pracy

wybranego
silnika:

*

= 30

+

*

= 1472

,-.

/+

*

= 270 0

Średnica

wału

silnika elektr.:

*

= 48

Max. Naprężenia
przy

skręcaniu

wałków:

= 251 2

1.6.

Częstotliwość obracania wału:

+ = 60 ∙ 10

3

∙ 4 ∙ = 38,2

,-.

/+

1.7.

Maksymalna i minimalna liczba obrotów silnika elektrycznego:

+

#$%

= + ∙ "

)#$%

= 477,5

,-.

/+

+

#&'

= + ∙ "

)#&'

= 3056

,-.

/+

1.8.

Dobór silnika elektrycznego:
Zgodnie z zasadą:

*

>

wybrano silnik

4SG 200 L-4 z katalogu firmy Tamel

1.9.

Rzeczywiste przełożenie układu napędowego:

"

)

=

+

*

+ = 38,485

1.10.

Rzeczywiste przełożenia poszczególnych przekładni:

•

Przekładnia pasowa:

"

6

= 2,65

•

Przekładnia zębata o zębach skośnych:

"

7

= 3,8

•

Przekładnia zębata o zębach prostych:

"

3

= 3,8

1.11.

Obciążenie wałów układu napędowego:

•

Przekładnia pasowa

Moc:

6

=

= 23,26

Prędkość obrotowa:

+

6

= +

*

= 1470

,-.

/+

Moment obrotowy:

8

6

= 9550 ∙

6

+

6

= 151,1

Średnica wału:

6

= 9

10

3

∙ 8

6

0,2 ∙

:

= 31,15

"

)

= 38,5

6

= 23,26

+

6

= 1470

,-.

/+

8

6

= 151,1

6

= 31,15

3

•

Przekładnia zębata o zębach skośnych

Moc:

7

=

6

∙

∙

ł

= 24,45

Prędkość obrotowa:

+

7

=

+

6

"

7

= 386,8

,-.

/+

Moment obrotowy:

8

7

= 9550 ∙

7

+

7

= 554,2

Średnica wału:

7

= 9

10

3

∙ 8

7

0,2 ∙

:

= 48,04

•

Przekładnia zębata o zębach prostych

Moc:

3

=

7

∙

∙

ł

= 21,67

Prędkość obrotowa:

+

3

=

+

7

"

3

= 101,8

,-.

/+

Moment obrotowy:

8

3

= 9550 ∙

3

+

3

= 2033

Średnica wału:

3

= 9

10

3

∙ 8

3

0,2 ∙

:

= 74,08

7

= 24,45

+

7

= 386,8

,-.

/+

8

7

= 554,2

7

= 48,04

3

= 21,67

+

7

= 101,8

,-.

/+

8

7

= 2033

7

= 74,08

2.

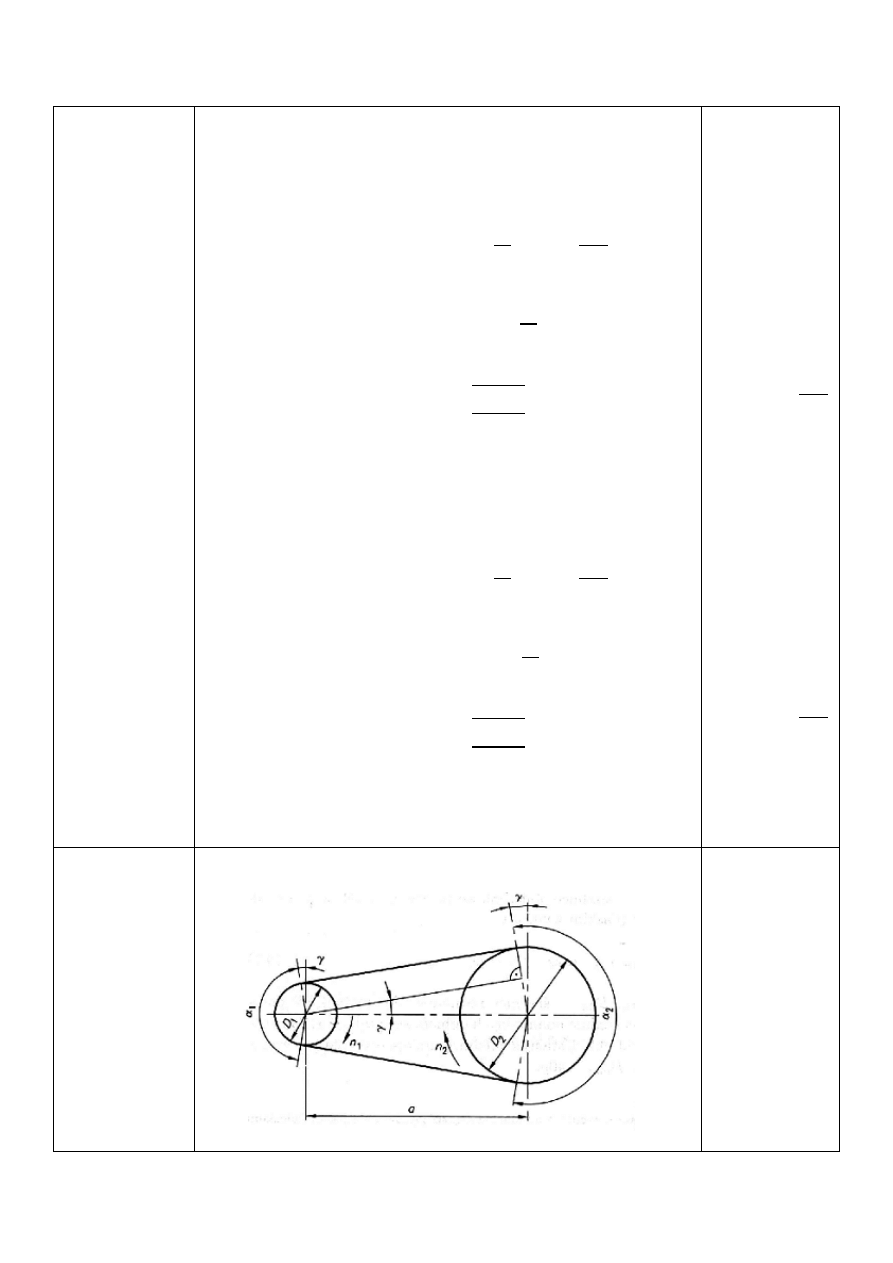
Obliczenia przekładni pasowej z pasem klinowym:

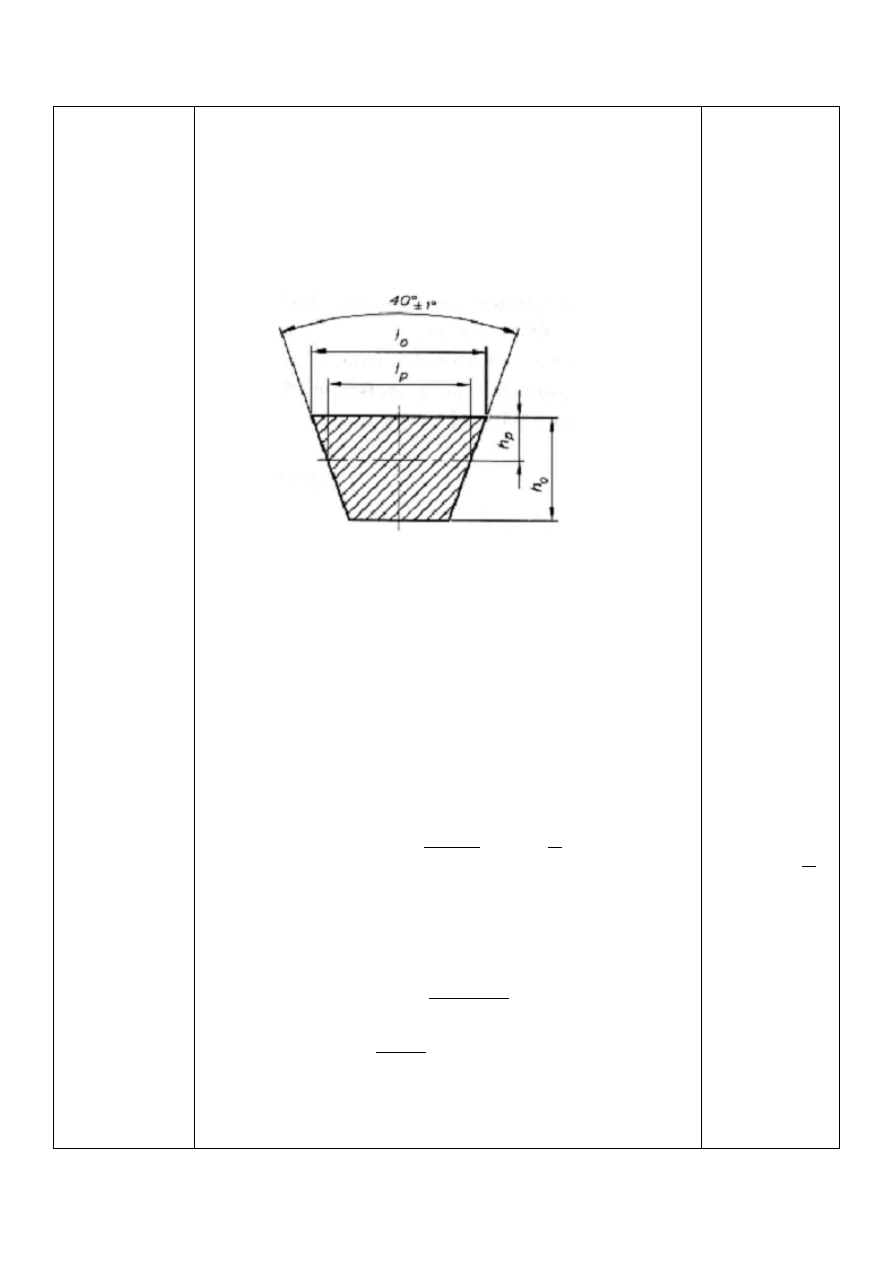
4

Współczynnik
uwzględniający
trwałość

pasa

klinowego:

;

= 1,2

<

)

= 22

< = 19

ℎ = 14

ℎ

*

= 5,7

Współczynnik
poślizgu
sprężystego:

> = 0,01

2.1.

Moment obliczeniowy

8

6

= 8

6

∙

;

= 181,33

2.2.

Moc obliczeniowa

6

=

6

∙

;

= 27,91

2.3.

Przekrój i wymiary przekroju pasa
Oznaczenie pasa: C, HC

2.4.

Minimalna średnica koła czynnego
Dobrano na podstawie [1], str. 121, tab. 7.3.1

?

6#$%

= 200

2.5.

Średnica skuteczna
Dobrano na podstawie [1], str. 117, tab. 7.2.5

?

6

= 224

2.6.

Średnica obliczeniowa koła biernego

?

7

= ?

6

∙ "

6

= 593,6

Na podstawie [1], str. 117, tab. 7.2.5

?

7

= 560

2.7.

Prędkość pasa i maksymalna prędkość pasa

=

4?

6

+

6

60 ∙ 10

3

= 17,24

Dla pasa o przekroju C maksymalna prędkość pasa wynosi 25
m/s.

2.8.

Przełożenie rzeczywiste przekładni

"

@

=

?

7

?

6

∙ A1 − >C = 2,525

Odchyłka:

∆" =

|F

GH

IF

J

|

F

J

= 0,047

Wartość odchyłki stanowi 1,8 % wartości przełożenia.

8

6

= 190

6

= 28

?

6

= 224

?

7

= 560

= 17,24

"

@

= 2,525

5

Współczynnik
uwzględniający
kąt opasania koła
czynnego ([1], str.
122, tab. 7.3.7):

&

= 1

Prędkość większa
od

wyliczonej

powyżej (17 m/s):

= 20

Moc

nominalna

dla tej prędkości
(tabela 7.3.4):

)

= 7,86

Prędkość mniejsza
od

wyliczonej

powyżej:

#

= 15

Moc

nominalna

dla tej prędkości
(tabela 7.3.4):

)#

= 6,95

2.9.

Zalecana odległość osi

2 ≥

&

∙ ?

7

2 = 560

2.10.

Obliczeniowa długość pasa

L′ = 2 ∙ 2 + 0,5 ∙ 4 ∙ A?

6

+ ?

7

C +

0,25 ∙ A?

7

− ?

6

C

7

2

L′ = 2402

2.11.

Rzeczywista długość pasa

Na podstawie [1], str.121, tab. 7.3.3 dobrano rzeczywistą
długość pasa spełniającą warunek:

L ≥ L′

L = 2500

2.12.

Rzeczywista odległość osi

2 = 2 + 0,5 ∙ OL − L′ P = 609,05

2.13.

Liczba obiegów pasa

Q = 10

3

∙ L = 6,9

1

2.14.

Kąt opasania koła czynnego

R

6

= 180 −

57 ∙ A?

7

− ?

6

C

2

= 148,6°

2.15.

Obliczeniowa moc przenoszona przez 1 pas

Na podstawie [1], str. 122, tab. 7.3.4, korzystając z metody
interpolacji liniowej wyznaczono wartość nominalnej mocy
przenoszonej przez 1 pas.

)

=

)#

+

A

)

−

)#

C

−

#

∙ A −

#

C = 7,36

2 = 560

L′ = 2402

L = 2500

2 = 609,05

Q = 6,9

1

R

6

= 148,6°

)

= 7,36

6

Współczynnik
uwzględniający
długość pasa:

T

= 0,94

Współczynnik
uwzględniający
kąt opasania koła
czynnego ([1], str.
122, tab. 7.3.6):

U

= 0,93

Współczynnik
uwzględniający
ilość pasów ([1],
str.

122,

tab.

7.3.8):

= 0,75

Współczynnik
napędu dla pasów
tkaninowo

–

gumowych
(stosunek
obciążenia
użytecznego

do

sumy napięć w
cięgnach):

V = 0,6

Moc przenoszona przez 1 pas wynosi:

6 &

=

)

∙

T

∙

U

= 6,43

2.16.

Obliczeniowa liczba pasów

W =

6

6 &

= 4,34

2.17.

Rzeczywista liczba pasów

W =

W

= 5,786

2.18.

Siła obwodowa

X

Y

= 2 ∙ 10

3

∙

8

6

?

6

= 1349

2.19.

Napięcie wstępne pasa

X

)

=

X

Y

2 ∙ V = 1124

2.20.

Siła obciążająca wały przekładni

X = 2 ∙ X

)

∙ /+ Z

[

2\ = 2222

2.21.

Napięcie cięgien

•

Czynnego:

X

6

= X

)

+ 0,5 ∙ X

Y

= 1799

•

Biernego:

X

7

= X

)

− 0,5 ∙ X

Y

= 449,7

2.22.

Kąt odchylenia pasa

] = 2.^ /+ _

?

7

− ?

6

22 ` = 16°

6 &

= 6,43

W = 4,34

W = 6

X

Y

= 1349

X

)

= 1124

X = 2222

X

6

= 1799

X

7

= 449,7

] = 16°

7

Dla

pasa

o

przekroju C ([2],
str. 409, tab. 9.4):

< = 19

-

#$%

= 5,7

ℎ

#$%

= 14

a = 25,5

b = 17

ℎ = 5,7

Współczynnik
przeciążenia:

c = 1,1

Pole

przekroju

pasa:

d

= 2,3 ∙ 10

Ie

7

Moduł
sprężystości:

f

g

= 391 2

Odległość
skrajnego włókna
od osi obojętnej
pasa (dla pasów
klinowych):

h

)

= ℎ

= 5,7

2.23.

Siła obciążająca wał i łożyska

= ZX

6

7

+ X

7

7

+ 2X

6

X

7

∙ ^, A2]C\

6

7

= 2583

2.24.

Kąt pochylenia siły Q względem osi koła

i = 2.^j0 _

X

6

− X

7

X

6

+ X

7

` ∙ j0] = 10°

2.25.

Siły działające na wał

= ∙ ^, i = 1994

= ∙ /+i = 341,6

3.

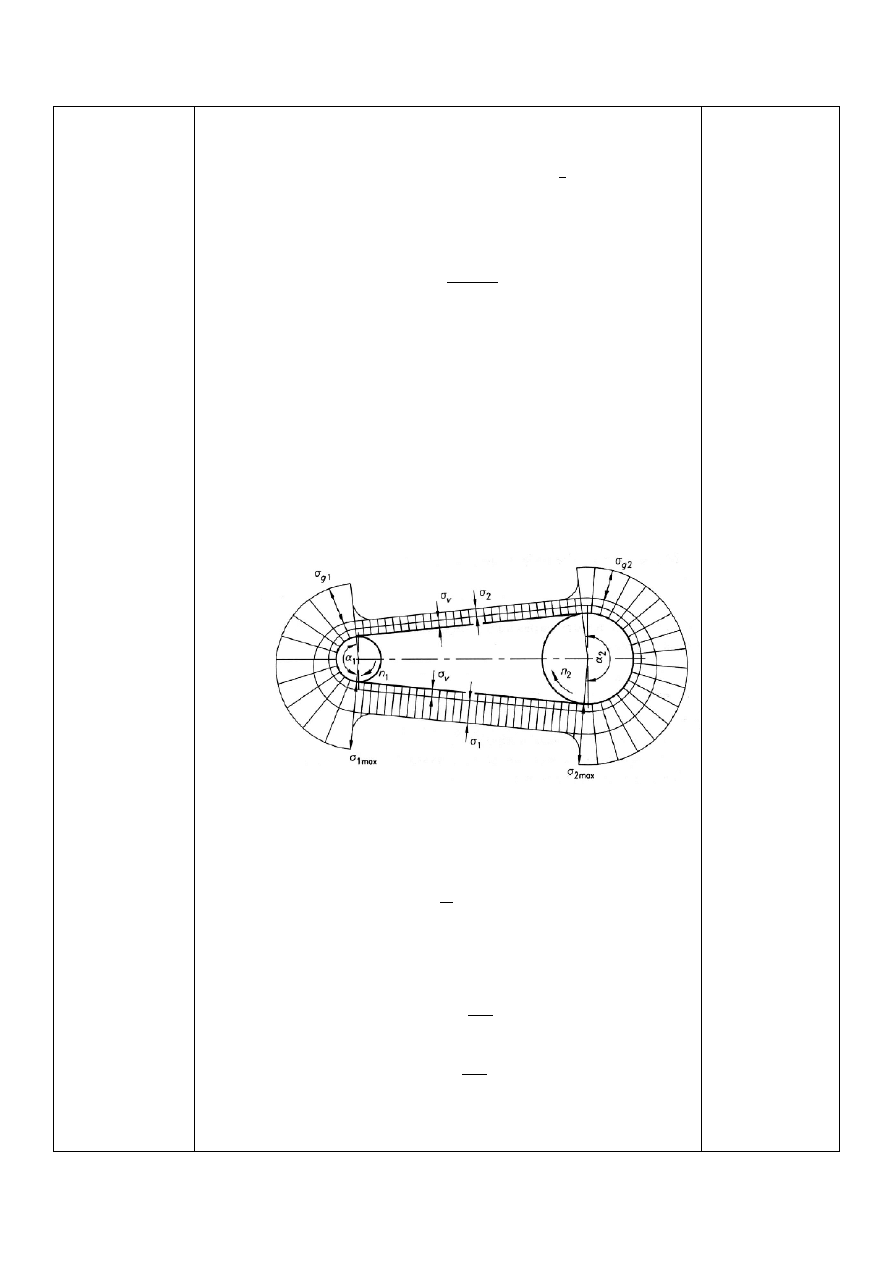
Wytrzymałość i trwałość pasów

3.1.

Naprężenia normalne w cięgnie czynnym od rozciągania siła F

1

k

6

= X

6

∙

c

d ∙ 10

Il

= 8,61 2

3.2.

Naprężenia normalne od zginania pasa

k

g6

= f

g

∙

2h

)

?

6

= 21 2

k

g7

= f

g

∙

2h

)

?

7

= 0,81 2

= 2023

i = 10°

= 1994

= 341,6

k

6

= 8,61 2

k

g6

= 21 2

k

g7

= 0,81 2

8

Na podst. [2], str.
417, tab. 9.7:

m = 1000

0

3

= 11

Wsp. zmienności
obciążenia:

>

7

= 2

Ilość kół:

W = 2

Naprężenia
dopuszczalne:

k

n

= 91 2

Obliczeniowa
trwałość

pasa

klinowego:

o

)

= 200 ∙ 10

l

Częstość

zmian

obciążenia:

b = 6pW

Ilość

zmian

w

ciągu doby:

+ = 2

3.3.

Naprężenia normalne wywołane siłą odśrodkową

k

q

=

m ∙

7

10

l

= 0,31 2

3.4.

Naprężenia maksymalne

•

Na mniejszym kole:

k

6#&'

= k

6

+ k

g6

+ k

q

= 10,91 2

•

Na większym kole:

k

7#&'

= k

6

+ k

g7

+ k

q

= 9,71 2

3.5.

Współczynnik uwzględniający zginanie pasa na kołach

>

6

=

2

1 + Zk

7#&'

k

6#&'

\

#

= 1,563

3.6.

Przewidywany czas pracy przekładni

8 = 9200 ∙

b

+ ∙ b = 4000ℎ

b =

1000

L

= 6,9pW

3.7.

Liczba cykli

o = 3600 ∙ 8 ∙ 0,001∙ L ∙

W

>

6

∙ >

7

= 6,36 ∙ 10

r

3.8.

Sprawdzenie warunku wytrzymałościowego

k

#&'

= k

n

∙ 9

o

)

o

s

= 9,91 2

Warunek wytrzymałościowy nie jest spełniony. Maksymalne wartości
naprężeń występujących podczas pracy przekładni są nieznacznie większe
od naprężeń dopuszczalnych. Obliczenia prowadzone były od początku z
nadwyżką wartości wyliczonych, więc prawdopodobne jest że warunek
wytrzymałościowy jest spełniony. Największe są wartości naprężeń
pochodzących od zginania pasa. Należałoby zastosować pas klinowy
zębaty, posiadający dużą odporność na zginanie. Drugim rozwiązaniem
jest zwiększenie średnic kół.

k

q

= 0,31 2

k

6#&'

= 10,91 2

k

7#&'

= 9,71 2

>

6

= 1,563

8 = 4000ℎ

o = 6,36 ∙ 10

r

k

#&'

= 9,91 2

9

Moc:

7

= 22,45

Prędkość
obrotowa:

+

7

= 386,84

,-.

/+

Moment
obrotowy:

8

7

= 554,2

Średnica wału:

7

= 48

Przełożenie
przekładni:

"

7

= 3,8

Wsp.

szerokości

wieńca:

= 1

Wsp.
zastosowania:

c

t

= 1,1

Wsp.
eksploatacyjny:

c

u

= c

t

= 1,1

4.

Obliczenia przekładni zębatej o zębach skośnych

Materiał na koło zębate: stal hartowana powierzchniowo 15CrNi6.
Naprężenia dopuszczalne dla tej stali wynoszą:

k

u $#

= 16301 2

k

v $#

= 5001 2

4.1.

Wstępne określenie naprężeń dopuszczalnych

a)

Do wstępnych obliczeń przyjmujemy naprężenia dopuszczalne:

k

uw

= 0,8 ∙ k

u $#

= 13041 2

k

vw

= 0,8 ∙ k

v $#

= 4001x2

b)

Trwałość przekładni:

Przekładnia pracuje 100 dni w roku, 10 godzin na dobę, przez 5
lat.

y = 100 ∙ 10 ∙ 5 = 5000ℎ

c)

Liczba cykli:

+

Y

= 60 ∙ y ∙ +

7

= 1,16 ∙ 10

z

4.2.

Wstępne określenie średnicy podziałowej zębnika

ę

= 690 ∙ 9

8

7

c

u

k

uw7

∙

"

7

+ 1

"

7

:

= 53

4.3.

Określenie odległości osi kół

2 =

ę

2 ∙ A1 + "

7

C = 121,17

Przyjmuję znormalizowaną odległość osi:

2 = 140

4.4.

Określenie podstawowych parametrów przekładni

6

=

2 ∙ 2

1 + "

7

= 58,3

Przyjmuję średnicę podziałową:

6

= 60

Przyjmuję liczbę zębów zębnika:

W

6

= 22

Przyjmuję kąt pochylenia linii zęba:

| = 15°

a)

Moduł normalny:

%

=

6

^, |

W

6

= 2,64

Przyjmuję moduł normalny:

%

= 2,75

k

uw

= 13041 2

k

vw

= 4001 2

y = 5000ℎ

+

Y

= 1,16 ∙ 10

z

ę

= 53

2 = 121,17

2 = 140

6

= 60

W

6

= 22

| = 15°

%

= 2,75

10

R = 20°

| = 15°

} ~

Y

= 0,5

b)

Moduł czołowy:

Y

=

%

^, | = 2,847

Przyjmuję moduł czołowy:

Y

= 3

d)

Liczba zębów koła zębatego:

W

7

= W

6

∙ "

7

= 83,6

e)

Średnice podziałowe kół zębatych:

6

=

Y

∙ W

6

= 66

7

=

Y

∙ W

7

= 252

f)

Nominalna odległość osi kół:

2

6

=

W

6

+ W

7

2 ∙

Y

= 159

Przyjmuję szerokość wieńca:

- = 60

g)

Czołowy kąt przyporu:

R

Y

= 2.^j0 _

j0R

^, |` = 21°

h)

Toczny kąt przyporu:

R

Y

= j0 _

2

6

2 ∙ ^, R

Y

`

I6

= 39°

i)

Zastępcza liczba zębów:

W

6

=

W

6

^,

3

| = 24,42

W

7

=

W

7

^,

3

| = 93,22

j)

Współczynniki przesunięcia zarysu:

Suma współczynników przesunięcia zarysu:

} ~

%

=

∑ ~

Y

^, | = 0,52

Na podstawie [2], str. 249, rys. 4.24 wyznaczono wartości:

~

6%

= 0,39

~

7%

= 0,12

Y

= 3

W

7

= 84

6

= 66

7

= 252

- = 60

R

Y

= 21°

R

Y

= 39°

W

6

= 24,42

W

7

= 93,22

11

h = 1

Współczynniki przesunięcia zarysu:

~

6Y

= ~

6%

∙ ^, | = 0,377

~

7Y

= } ~

Y

− ~

6Y

= 0,123

4.5.

Obliczenie wskaźnika zazębienia przekładni

a)

Wysokości głów zębów:

ℎ

&6

=

%

Ah + ~

6%

C = 3,82

ℎ

&7

=

%

Ah + ~

7%

C = 3,08

b)

Wartości pomocnicze:

€

6

=

1

24

9•1 + 2 ∙ ℎ

&6

6

‚

7

•1 +

j0

7

R

^,

7

|‚ − 1 = 0,1

€

6

=

1

24

9•1 + 2 ∙ ℎ

&7

7

‚

7

•1 +

j0

7

R

^,

7

|‚ − 1 = 0,11

€

3

=

2 ∙ /+R

Y

4 ∙

Y

∙ ^, R

Y

= 8,39

c)

Czołowy wskaźnik zazębienia:

>

U

= W

6

∙ €

6

+ W

7

∙ €

7

− €

3

= 2,97

d)

Skokowy wskaźnik zazębienia:

>

ƒ

=

- ∙ /+|

4 ∙

%

= 1,8

e)

Całkowity wskaźnik zazębienia:

>

„

= >

U

+ >

ƒ

= 4,765

f)

Kąt pochylenia linii zęba na walcu zasadniczym:

| = 2.^j0Aj0| ∙ ^, RC = 14°

~

6Y

= 0,377

~

7Y

= 0,123

ℎ

&6

= 3,82

ℎ

&7

= 3,08

€

6

= 0,1

€

7

= 0,11

€

3

= 8,39

>

U

= 2,97

>

ƒ

= 1,8

>

„

= 4,765

| = 14°

12

Na podstawie [2],
str. 228, tab. 4.4
dobrano
współczynniki (6
klasa
dokładności):

c

6

= 13,3

c

7

= 0,0087

g)

Współczynniki Y

ε

i Z

ε

:

…

*

= 0,25 +

0,75

>

U

∙ ^,

7

| = 0,488

†

*

= 9

1

>

U

= 0,581

4.6.

Obliczenia obciążenia zębów

a)

Nominalna siła obwodowa:

6

=

20008

7

6

= 18470

b)

Przybliżona wartość prędkości rezonansowej:

+

‡

= A2,1 ÷ 2,4C ∙ 10

r

∙

^, |

W

67

∙

%

∙

"

7

+ 1

"

7

= A1,93 ÷ 2,2C ∙ 10

e

,-.

/+

Przekładnia pracuje w zakresie podrezonansowym, ponieważ:

386,8

,-.

/+< 0,7 ∙ +

‡

c)

Wskaźnik obciążenia jednostkowego:

Š =

c

t

∙

6

- = 338,68

d)

Wskaźnik prędkości przekładni W:

=

W

6

∙

100

9 "

77

"

77

+ 1 = 0,26

Gdzie:

=

4

6

+

7

60 ∙ 1000 = 1,22

e)

Współczynnik dynamiczny:

c

q

= 1 + _

c

6

Š + c

7

` = 1,012

…

*

= 0,488

†

*

= 0,581

6

= 18470

Š = 338,68

= 0,26

c

q

= 1,012

13

Na podst. [2], str.
229-230, tab. 4.5,
4.6

dobrano

współczynniki:

c

uU

= 1

c

vU

= c

uU

d

6

= 1,05

d

7

= 3,8

f)

Współczynniki nierównomierności obciążenia:

c

uƒ

= d

6

+ 0,31 _

-

6

`

7

+ d

7

∙ 10

Ie

∙ - = 1,383

c

vƒ

= c

uƒ

‹

Œ

= 1,338

Gdzie:

v

=

Z-ℎ\

7

1 + -ℎ + Z

-

ℎ\

7

= 0,898

ℎ = 2,25 ∙

%

= 6,188

g)

Sprawdzenie współczynnika bezpieczeństwa na nacisk
stykowy S

H

:

•

u

=

k

u $#

†

u

†

‡

†

Ž

†

ƒ

•

6

- ∙

6

∙ "

7

+ 1

"

7

∙

†

‹;

†

T

†

•

†

‘

†

’

†

“

”c

t

c

‘

c

uƒ

c

uU

= 2,526

Gdzie:

•

Dobrane koła są szlifowane o chropowatości

•

–

= 4— , więc współczynniki uwzględniające wpływ

różnic w smarowaniu, chropowatości powierzchni
zębów,

szybkości

pracy

między

warunkami

modelowymi a rzeczywistymi warunkami pracy na
wytrzymałość zmęczeniową wynoszą:

†

T

†

•

†

‘

= 1

•

Dla kół hartowanych współczynnik twardości wynosi:

†

’

= 1

•

Współczynnik Z

x

dobrany został na podstawie [2], str.

239, rys. 4.21:

†

“

= 1

•

Współczynnik Z

E

dobrany na podstawie [2], str. 235,

tab. 4.7:

†

‡

= 189,81 2

6

7

•

Współczynnik uwzględniający kąt pochylenia linii zęba i
stopnia pokrycia:

†

Ž

= 9

1

>

U

= 0,581

c

uƒ

= 1,383

c

vƒ

= 1,338

•

u

= 2,526

14

•

Współczynnik trwałości zmęczeniowej wynosi 1,
ponieważ przekładnia pracuje w zakresie trwałej
wytrzymałości zmęczeniowej:

†

‹;

= 1

•

Współczynniki Z

H

i Z

β:

†

u

=

1

^, R

Y

9

2^, |

j0R

Y

= 1,886

†

ƒ

= ”^, | = 0,983

h)

Współczynnik bezpieczeństwa na zginanie:

•

v

=

k

v $#

6

- ∙

%

∙ c

t

c

‘

c

vƒ

c

vU

∙

…

˜;

…

‹;

…

™@* ;

…

“

…

v˜

…

Ž

…

ƒ

= 3,12

Gdzie:

•

Współczynnik uwzględniający wpływ kształtu zęba i
karbu ([2], str. 233, rys. 4.15):

…

v˜

= 3,95

Na wykresie znajdujemy się w polu

Š > 1,5, więc:

…

™@* ;

= 1

•

Współczynnik wielkości:
Na podstawie [2], str. 238, rys. 4.19

…

“

= 1

…

˜;

= 2

•

Współczynnik Y

β

:

…

ƒ

= 1 −

|

120 = 0,998

•

Współczynnik Y

NT

:

Na podst. [2], str. 236, rys. 4.17

…

‹;

= 1

•

Współczynnik Y

ε

:

…

Ž

= 0,25 +

0,75

>

U

^,

7

| = 0,488

•

v

= 3,12

15

4.7.

Sprawdzenie zębów na zagrzanie

;

=

7

Z1 + 1

"

7

\

7W

6

= 0,184

~

;

=

W

6 %

-

1000

;

= 19,714

4.8.

Obliczenie nominalnych wartości sił działających na wały i
łożyska

a)

Kąt pochylenia linii zęba na okręgu tocznym:

| = 2.^j0 Z

2

2 j0|\ = 16°36′

b)

Wartości sił:

@

= 1000

7

∙ j0R

Y

= 13980

&

= 1000

7

∙ j0| = 6627

4.9.

Zestawienie obliczonych wielkości

•

Odległość osi kół:

2 = 140

•

Liczba zębów kół:

W

6

= 22

W

7

= 84

•

Moduł normalny:

%

= 2,75

•

Szerokość wieńca:

- = 60

•

Średnice podziałowe kół:

6

= 66

7

= 252

•

Średnice okręgów wierzchołków zębów:

&6

=

%

AW

6

+ 2C

^, |

= 68,33

&7

=

%

AW

7

+ 2C

^, |

= 256,25

;

= 0,184

~

;

= 19,714

| = 16°36′

@

= 13980

&

= 6627

16

•

Średnice okręgów głów zębów:

š6

=

%

AW

6

− 2,5C

^, |

= 55,52

š7

=

%

AW

7

− 2,5C

^, |

= 243,43

Moc:

3

= 21,67

Prędkość
obrotowa:

+

3

= 101,8

,-.

/+

Moment
obrotowy:

8

7

= 2033

Średnica wału:

7

= 74,1

Przełożenie
przekładni:

"

3

= 3,8

Wsp.

szerokości

wieńca:

= 1

Wsp.
zastosowania:

c

t

= 1,1

Wsp.
eksploatacyjny:

c

u

= c

t

= 1,1

5.

Obliczenia przekładni zębatej o zębach prostych

Materiał na koło zębate: stal hartowana powierzchniowo 15CrNi6.
Naprężenia dopuszczalne dla tej stali wynoszą:

k

u $#

= 12801 2

k

v $#

= 3101 2

5.1.

Wstępne określenie naprężeń dopuszczalnych

a)

Do wstępnych obliczeń przyjmujemy naprężenia dopuszczalne:

k

uw

= 0,8 ∙ k

u $#

= 10241 2

k

vw

= 0,8 ∙ k

v $#

= 2481x2

b)

Trwałość przekładni:

Przekładnia pracuje 100 dni w roku, 10 godzin na dobę, przez 5
lat.

y = 100 ∙ 10 ∙ 5 = 5000ℎ

c)

Liczba cykli:

+

Y

= 60 ∙ y ∙ +

3

= 3,05 ∙ 10

r

5.2.

Wstępne określenie średnicy podziałowej zębnika

ę

= 690 ∙ 9

8

3

c

u

k

uw7

∙

"

3

+ 1

"

3

:

= 96

5.3.

Określenie odległości osi kół

2 =

ę

2 ∙ A1 + "

3

C = 230,4

Przyjmuję znormalizowaną odległość osi:

2 = 250

k

uw

= 10241 2

k

vw

= 2481 2

y = 5000ℎ

+

Y

= 3,05 ∙ 10

r

ę

= 96

2 = 230,4

2 = 250

17

Na podst. [2], str.
239, rys. 4.25:

~

6

= 0,52

~

7

= 0,49

R = 20°

5.4.

Określenie podstawowych parametrów przekładni

6

=

2 ∙ 2

1 + "

3

= 104,17

Przyjmuję średnicę podziałową:

6

= 105

Przyjmuję liczbę zębów zębnika:

W

6

= 37

a)

Moduł:

=

6

W

6

= 2,84

Przyjmuję moduł normalny:

= 2,75

b)

Liczba zębów koła zębatego:

W

7

= W

6

∙ "

3

= 140,6

c)

Średnice podziałowe kół zębatych:

6

= ∙ W

6

= 102

7

= ∙ W

7

= 387,8

d)

Nominalna odległość osi kół:

2

6

=

W

6

+ W

7

2

∙ = 244,75

Przyjmuję szerokość wieńca:

- = 80

5.5.

Ustalenie przesunięcia współczynników zarysu

a)

Różnice między nominalną i rzeczywistą odległością osi
usuwamy za pomocą korekcji typu P:

›

@

=

2 − 2

6

2

6

= 0,021

› = ›

@

”1 + 7›

@

= 0,023

} ~ = 0,5› ∙ AW

6

+ W

7

C = 2,05

6

= 0,5O› − ›

@

PAW

6

+ W

7

C = 0,138

b)

Toczny kąt przyporu:

R = 2.^^, _

2

6

2 ^, R` = 23°

6

= 105

W

6

= 37

W

7

= 141

2

6

= 244,75

- = 80

›

@

= 0,021

› = 0,023

} ~ = 2,05

6

= 0,138

R = 23°

18

h = 1

5.6.

Obliczenie wskaźnika zazębienia przekładni

a)

Wysokości głów zębów:

ℎ

&6

= A~

6

+ hC = 4,18

ℎ

&7

= A~

7

+ hC = 4,10

b)

Współczynnik zazębienia przekładni:

>

U

=

W

6

24

9•1 + 2ℎ

&6

6

‚

7

∙

1

^,

7

R − 1 +

+

W

7

24

9•1 + 2ℎ

&7

7

‚

7

∙

1

^,

7

R − 1 −

2 ∙ /+R

4 ∙ ∙ ^, R = 0,835

c)

Współczynniki Y

ε

i Z

ε

:

…

Ž

= 0,25 +

0,75

>

U

= 1,15

†

Ž

= 9

4 − >

U

3 = 1,03

5.7.

Obliczenia obciążenia zębów

a)

Momenty obrotowe:

8

3

= 2033

b)

Nominalna siła obwodowa:

=

2000 ∙ 8

3

+

3

= 39940

c)

Przybliżona wartość prędkości rezonansowej:

+

‡

= A2,1 ÷ 2,4C ∙ 10

r

∙

^, |

W

6

∙ ∙

"

3

+ 1

"

3

= A7,05 ÷ 8,05C ∙ 10

3

d)

Wskaźnik obciążenia jednostkowego:

Š =

c

t

- = 549,2

ℎ

&6

= 4,18

ℎ

&7

= 4,10

>

U

= 0,835

…

Ž

= 1,15

†

Ž

= 1,03

8

3

= 2033

= 39940

Š = 549,2

19

Na podst. [2], str.
228, tab. 4.4:

c

6

= 14,9

c

7

= 0,0193

Na podst. [2], str.
229-230, tab. 4.5,
4.6

dobrano

współczynniki:

c

uU

= 1

c

vU

= c

uU

d

6

= 1,05

d

7

= 3,8

e)

Wskaźnik prędkości przekładni W:

=

4

6

+

3

60 ∙ 100 = 5,6

=

W

6

100

9 "

37

"

37

+ 1 = 2

f)

Współczynnik dynamiczny K

v

:

c

q

= 1 + _

c

6

Š + c

7

` = 1,05

g)

Współczynniki nierównomierności rozkładu obciążenia:

c

uƒ

= d

6

+ 0,26 _

-

6

`

7

+ d

7

∙ 10

e

∙ - = 1,23

c

vƒ

= c

uƒ

‹

Œ

= 1,21

Gdzie:

v

=

Z-ℎ\

7

1 + -ℎ + Z

-

ℎ\

7

= 0,92

ℎ = 2,25 = 6,2

h)

Sprawdzenie współczynnika na nacisk stykowy:

•

u

=

k

u $#

†

u

†

‡

†

Ž

†

ƒ

∙ •-

6

∙ "

3

+ 1

"

3

∙

†

‹;

†

T

†

•

†

‘

†

’

†

“

”c

t

c

‘

c

uƒ

c

uU

= 0,956

Gdzie:

•

Stosowane koła są szlifowane o chropowatości

• = 4— , więc współczynniki uwzględniające wpływ
różnic w smarowaniu, chropowatości powierzchni
zębów,

szybkości

pracy

między

warunkami

modelowymi a rzeczywistymi warunkami pracy na
wytrzymałość zmęczeniową wynoszą:

†

T

†

•

†

‘

= 1

•

Dla kół hartowanych współczynnik twardości wynosi:

†

’

= 1

= 5,6

= 2

c

q

= 1,05

c

uƒ

= 1,23

c

vƒ

= 1,21

•

u

= 0,956

20

•

Współczynnik Z

x

odczytany został z rys. 4.21, str. 239,

[2]:

†

“

= 1

•

Współczynnik Z

E

odczytany został z tab. 4.7, str. 235,

[2]:

†

‡

= 189,81 2

6

7

•

Współczynnik uwzględniający kąt pochylenia linii zęba i
stopnia pokrycia:

†

Ž

= 9

4 − >

U

3 = 1,03

•

Współczynnik trwałości wynosi 1, ponieważ przekładnia
pracuje w zakresie trwałej wytrzymałości zmęczeniowej:

†

‹;

= 1

•

Współczynnik Z

H

i Z

β

:

†

u

= 9

2

/+R ∙ ^, R = 2,355

Dla zębów prostych:

†

ƒ

= 1

i)

Współczynnik bezpieczeństwa na zginanie:

•

v

=

k

v $#

- ∙ c

t

c

‘

c

vƒ

c

vU

∙

…

˜;

…

‹;

…

™@* ;

…

“

…

v˜

…

Ž

…

ƒ

= 0,569

Gdzie:

•

Współczynnik uwzględniający wpływ kształtu zęba i
karbu ([2], str. 233, rys. 4.15):

…

v˜

= 3,75

•

Na wykresie znajdujemy się w polu

Š > 1,5, więc:

…

™@* ;

= 1

•

v

= 0,569

21

•

Współczynnik wielkości:
Na podst. [2], str. 238, rys. 4.19

…

“

= 1

…

˜;

= 2

•

Współczynnik Y

β

dla zębów prostych:

…

ƒ

= 1

•

Współczynnik Y

NT

:

Na podst. [2], str. 236, rys. 4.17

…

‹;

= 1

•

Współczynnik Y

ε

:

…

Ž

= 0,25 +

0,75

>

U

= 1,15

5.8.

Sprawdzenie zębów na zagrzanie

;

=

3

Z1 + 1

"

3

\

7W

6

= 0,106

~

;

=

W

6

-

1000

;

= 77,03

5.9.

Obliczenie nominalnych wartości sił działających na wały i
łożyska

@

= ∙ j0R = 17020

&

= ^, R = 43410

5.10.

Zestawienie obliczonych wielkości

•

Odległość osi kół:

2 = 250

•

Liczba zębów kół:

W

6

= 37

W

7

= 141

;

= 0,106

~

;

= 77,03

@

= 17020

&

= 43410

22

•

Moduł:

= 2,75

•

Szerokość wieńca:

- = 80

•

Średnice podziałowe kół:

6

= 101,75

7

= 387,75

•

Średnice okręgów wierzchołków zębów:

&6

= AW

6

+ 2C = 107,25

&7

= AW

7

+ 2C = 393,25

•

Średnice okręgów głów zębów:

š6

= AW

6

− 2,5C = 94,88

š7

= AW

7

− 2,5C = 380,88

Średnica
pierwszego wału:

6

= 35

2 = 140

6.

Rozplanowanie wewnętrzne reduktora

6.1.

Długość piasty:

L = 1,6

6

= 56

6.2.

Średnica piasty:

? = 1,7

6

= 59,5

6.3.

Grubość ścianki reduktora:

œ = 0,025 ∙ 2 + 3 = 6,5

6.4.

Odległość od wewnętrznej powierzchni ściany reduktora:

•

do bocznej powierzchni obracającej się części:

a = 1,2œ = 7,8

•

do bocznej powierzchni łożyska tocznego:

a

6

= 4

L = 56

? = 59,5

œ = 6,5

a = 7,8

a

6

= 4

23

%

= 2,75

6.5.

Odległość w osiowym kierunku między obracającymi się
częściami:

•

1 wał:

a

7

= 4

•

Na różnych wałach:

a

3

= 0,8œ = 5,2

6.6.

Promieniowa odległość miedzy kołem zębatym pierwszego
stopnia a wałem drugiego:

a

e

= 1,9œ = 12,4

6.7.

Promieniowa odległość od wierzchołków kół zębatych:

•

Do wewnętrznej powierzchni ścianki korpusu:

a

•

= 1,2œ = 7,8

•

Do wewnętrznej dolnej ścianki korpusu:

a

l

= 8

%

= 22

6.8.

Odległość od bocznych powierzchni części obracających się
razem z wałem do nieruchomych części zewnętrznych reduktora:

a

r

= 7

6.9.

Szerokość kołnierzy K łączonych śrubą o średnicy d

śr

:

ś@

= 1,5œ = 9,75

c = 28

6.10.

Sumaryczna szerokość kołnierzy:

= c + œ + 3 = 38,5

6.11.

Grubość kołnierza pokrywy bocznej:

ℎ

6

= 8

6.12.

Wysokość łba śruby:

ℎ = 0,8ℎ

6

= 6,4

6.13.

Grubość tulei:

ℎ

3

= 7

a

7

= 4

a

3

= 5,2

a

e

= 12,4

a

•

= 7,8

a

l

= 22

a

r

= 7

ś@

= 10

= 38,5

ℎ

6

= 8

ℎ = 6,4

ℎ

3

= 7

24

Szerokość
dobranego
łożyska:

- = 20

Szerokość wieńca
przekładni

z

zębami prostymi:

-

6

= 80

Szerokość wieńca
przekładni

z

zębami skośnymi:

-

7

= 60

6.14.

Grubość kołnierza tulei:

ℎ

7

= ℎ

6

= 8

6.15.

Odległość od bocznej powierzchni łożyska do bocznej

powierzchni nakładanej pokrywy dobiera się konstrukcyjnie:

ℎ

e#$%

= 5

ℎ

e

= 10

6.16.

Odległość między bocznymi powierzchniami łożysk

montowanych parami:

ℎ

•

= 4

6.17.

Wyznaczenie długości odcinków wału:

L

6

= L + a

r

+ ℎ + + ℎ

6

− a

6

− 0,5- = 52

L = a

6

+ 0,5- + a + -

6

+ a

7

+ L + a + a

6

+ 0,5- = 184

L

3

= a

6

+ 0,5- + a + 0,5-

7

= 52

Podczas wykonywania obliczeń okazało się, że wyznaczone wyżej
długości poszczególnych odcinków wałów uniemożliwiają osadzenie na
nich obliczonych powyżej przekładni zębatych. Długości te zostały
dobrane jeszcze raz oraz obliczenia wałów zostały przeprowadzone
ponownie. Tok obliczeniowy przedstawiony jest w dalszej części
projektu.

ℎ

7

= 8

ℎ

e

= 10

L

6

= 52

L = 184

L

3

= 52

25

@

= 13980

&

= 6627

= 18470

L

6

= 52

L

7

= 190

L

3

= 70

Średnica
podziałowa
zębnika o zębach
skośnych:

6

= 66

7.

Obliczenie pierwszego wału

Materiał wału: stal 45H o dopuszczalnych naprężeniach:

•

Na zginanie:

g

= 6101 2

•

Na skręcanie:

= 6601 2

7.1.

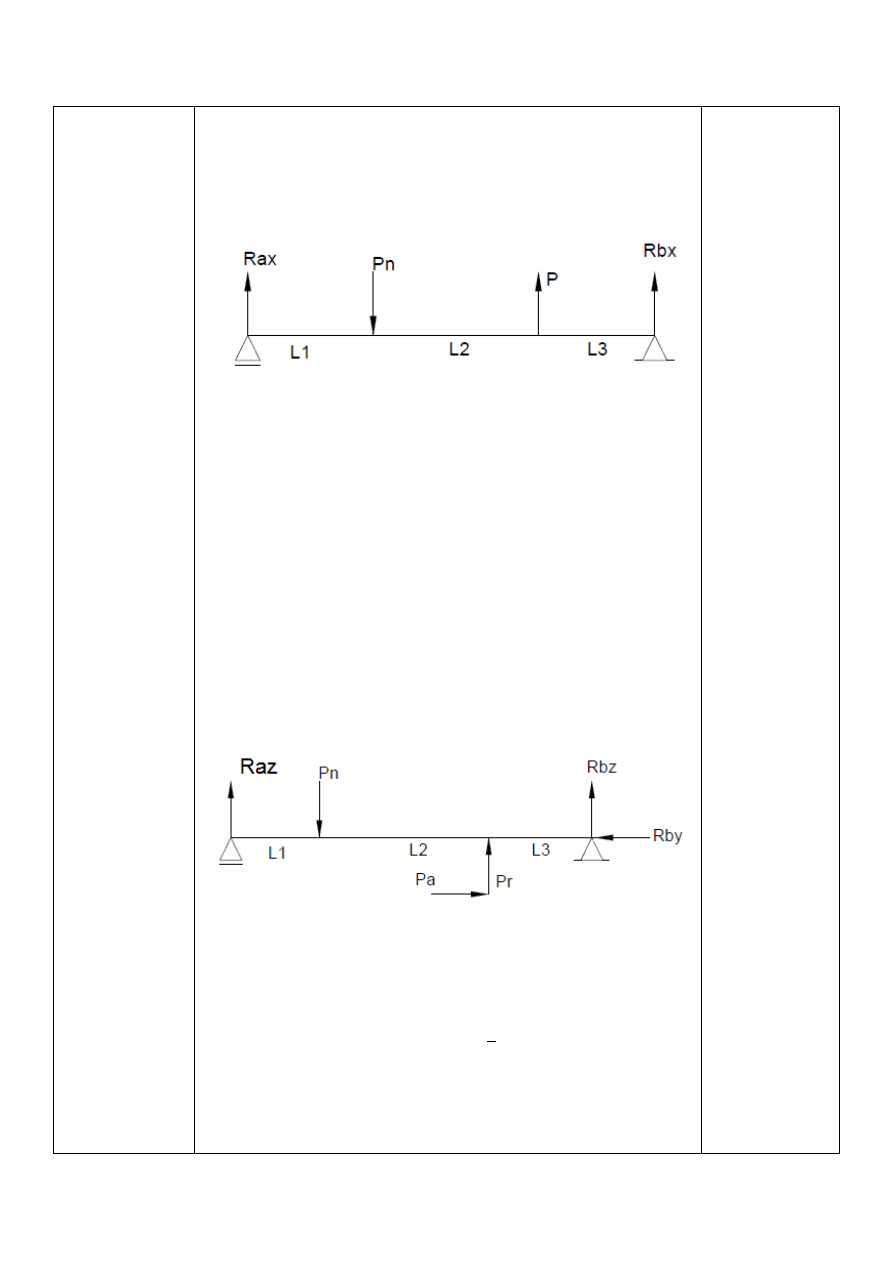
Wyznaczenie reakcji w podporach

•

Siły działające w płaszczyźnie xy:

Równania reakcji są następujące:

} X

'

= •

&'

− + •

'

= 0

} X = 0

} 1 = − ∙ L

3

+ •

&'

AL

7

+ L

3

C = 0

Po przekształceniu otrzymano wartości sił w podporach:

•

&'

= 4972

•

'

= 13500

•

Siły działające w płaszczyźnie zy:

Równania reakcji są następujące:

} X = •

&

−

@

+ • = 0

} X = • −

&

= 0

} 1 = −

@

∙ L

3

+

&

∙

1

2

6

+ •

&

AL

7

+ L

3

C = 0

•

&'

= 4972

•

'

= 13500

26

Po przekształceniu otrzymano wartości sił w podporach:

•

&

= 2923

• = 6627

• = 11057

7.2.

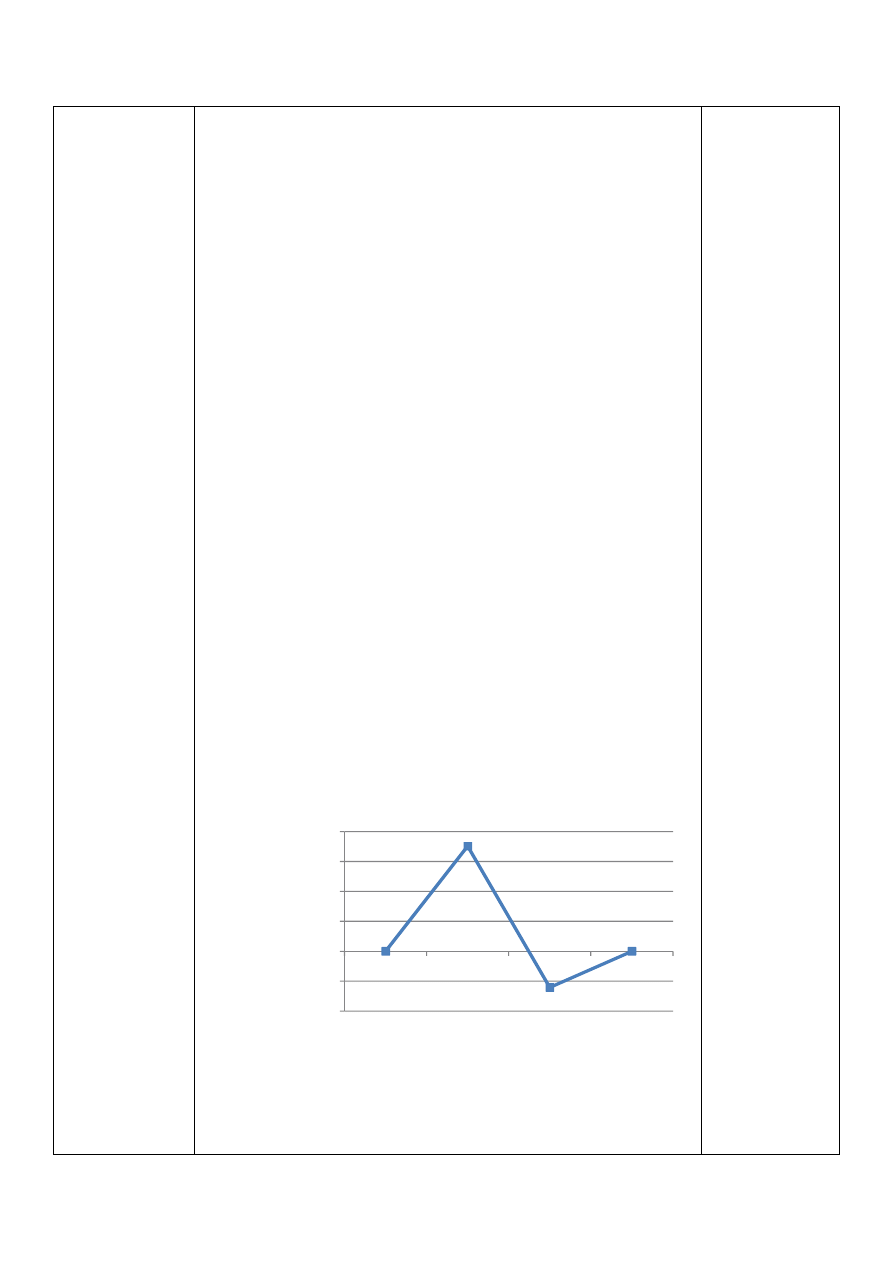
Obliczenie momentów gnących:

•

Płaszczyzna xy:

Dla:

0 ≤ ~ ≤ 52

1

g,'

A~C = •

'

∙ ~

1

g,'

A0C = 0

1

g,'

A52C = 702

Dla:

52

≤ ~ ≤ 242

1

g,'

A~C = •

'

∙ ~ − A~ − 52C

1

g,'

A52C = 702

1

g,'

A242C = −242

Dla:

242

≤ ~ ≤ 312

1

g,'

A~C = •

'

∙ ~ − A~ − 52C + •

&'

A~ − 242C

1

g,'

A242C = −242

1

g,'

A312C = 0

•

&

= 2923

• = 6627

• = 11057

-400

-200

0

200

400

600

800

0

52

242

312

M

o

m

e

n

t

g

n

ąc

y

,

N

m

x, mm

Momenty gnące w płaszczyźnie xy

27

•

Płaszczyzna zy:

Dla:

0 ≤ ~ ≤ 52

1

g,

A~C = • ∙ ~

1

g,

A0C = 0

1

g,

A52C = 575

Dla:

52

≤ ~ ≤ 242

1

g,

A~C = • ∙ ~ −

@

A~ − 52C + 0,5

6

∙

&

1

g,

A52C = 793

1

g,

A242C = 240

Dla:

242

≤ ~ ≤ 312

1

g,

A~C = • ∙ ~ −

@

A~ − 52C + 0,5

6

∙

&

+ •

&

A~ − 242C

1

g,

A242C = 240

1

g,

A312C = 0

7.3.

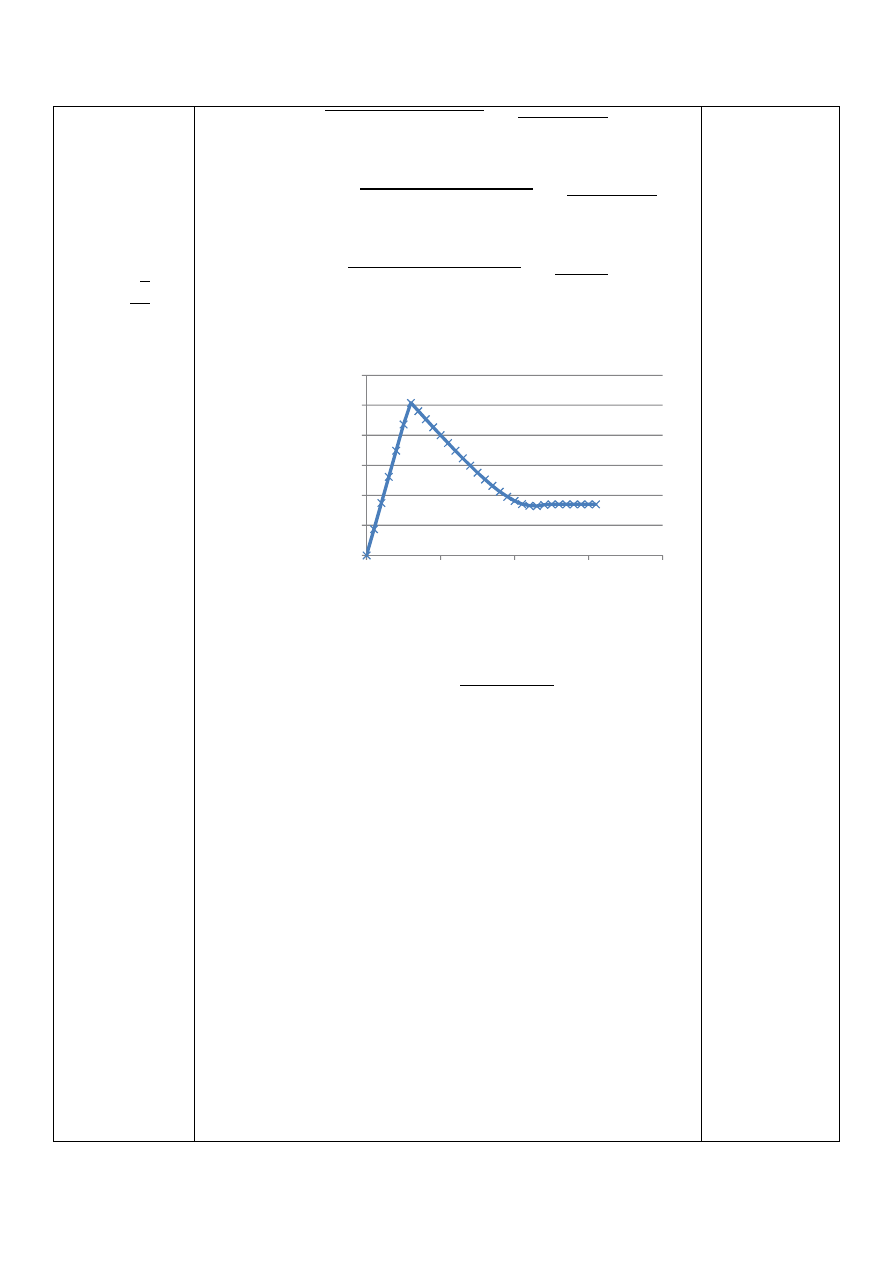
Obliczenie momentu zastępczego

Momenty gnące w charakterystycznych punktach wału: początek
wału, podpory oraz występujące siły.

1

g6

= •1

g,' A)C

7

+ 1

g, A)C

7

= ”0

7

+ 0

7

= 0

0

100

200

300

400

500

600

700

800

900

0

100

200

300

400

M

o

m

e

n

t

g

n

ąc

y

,

N

m

x, mm

Momenty gnące w płaszczyźnie zy

28

Dla

zmiennego

kierunku
obracania wału:

R = √

3

2

Dopuszczalne
naprężenia

przy

zginaniu:

g

= 1201 2

Dopuszczalne
naprężenia

przy

skręcaniu:

= 1301 2

1

g7

= •1

g,' A•7C

7

+ 1

g, A•7C

7

= ”702

7

+ 793

7

= 1059

1

g3

= •1

g,' A7e7C

7

+ 1

g, A7e7C

7

= ”242

7

+ 240

7

= 341

1

ge

= •1

g,' A367C

7

+ 1

g, A367C

7

= ”0

7

+ 0

7

= 0

Moment zastępczy obliczony został ze wzoru:

1

$

= •1

g$

7

+ AR8C

7

Wartości momentów zastępczych w poszczególnych punktach
wynoszą:

1

6

= 6287

1

7

= 6354

1

3

= 6296

1

e

= 6296

0,00

200,00

400,00

600,00

800,00

1000,00

1200,00

0

100

200

300

400

M

o

m

e

n

t

g

n

ąc

y

,

N

m

x, mm

Zastępczy moment gnący

29

7.4.

Dobór średnic wału

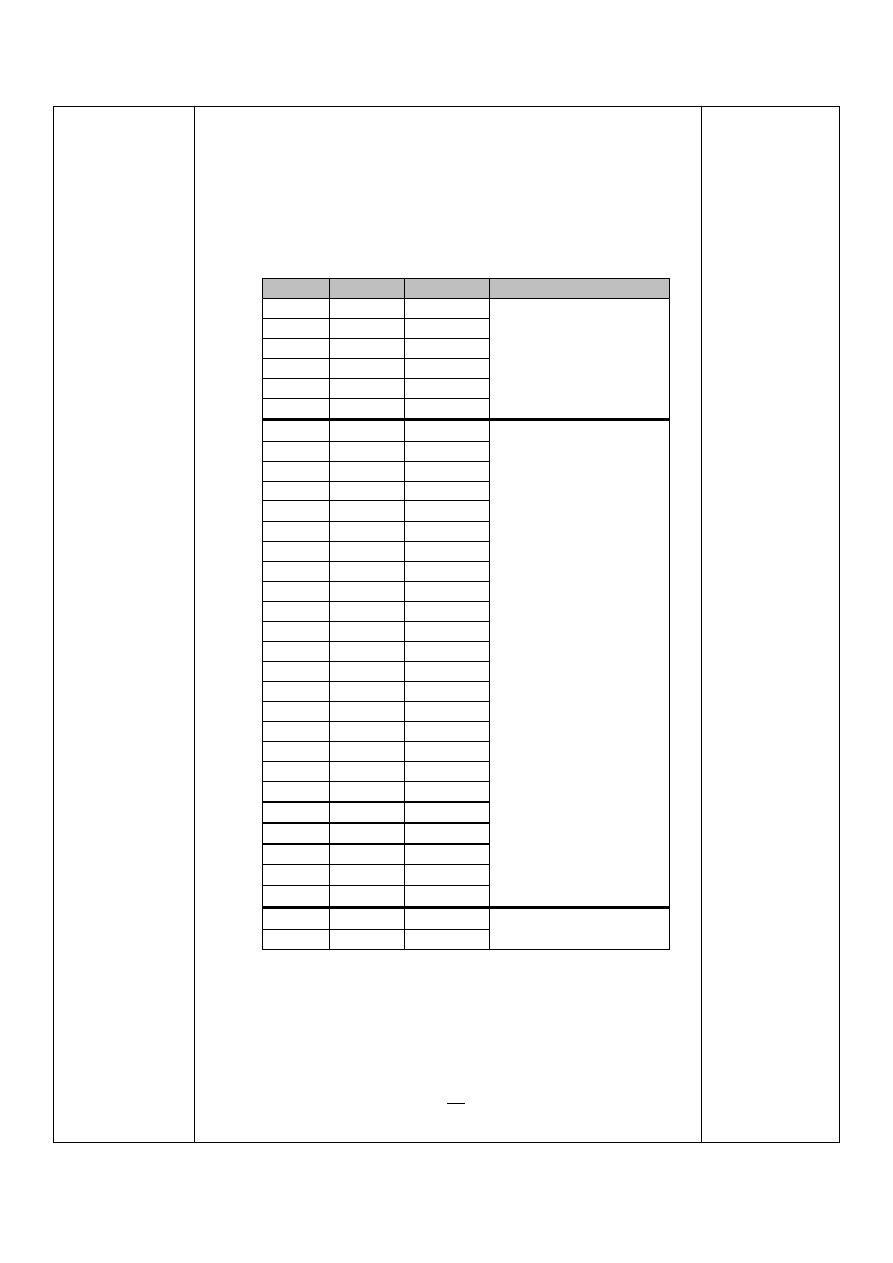
W tabeli poniżej znajduje się zestawienie obliczonych
momentów zastępczych oraz średnic wału. Obok podano
dobraną średnicę.

¡, ¢¢ £

¤

, ¥¢ ¦

§¨©

, ¢¢ Dobrana średnica, mm

0

6287,34

44,67

47

10

6289,77

44,68

20

6297,02

44,69

30

6309,10

44,72

40

6325,97

44,76

50

6347,60

44,82

60

6368,88

44,87

50

70

6360,43

44,85

80

6352,49

44,83

90

6345,07

44,81

100

6338,17

44,79

110

6331,78

44,78

120

6325,91

44,76

130

6320,56

44,75

140

6315,73

44,74

150

6311,43

44,73

160

6307,65

44,72

170

6304,40

44,71

180

6301,67

44,71

190

6299,47

44,70

200

6297,79

44,70

210

6296,64

44,69

220

6296,03

44,69

230

6295,93

44,69

240

6296,37

44,69

250

6296,52

44,69

260

6296,52

44,69

270

6296,52

44,69

280

6296,52

44,69

290

6296,52

44,69

300

6296,52

44,69

48

310

6296,52

44,69

Średnice wału dobrane zostały zgodnie z warunkiem:

7
6

≤ 1,2

30

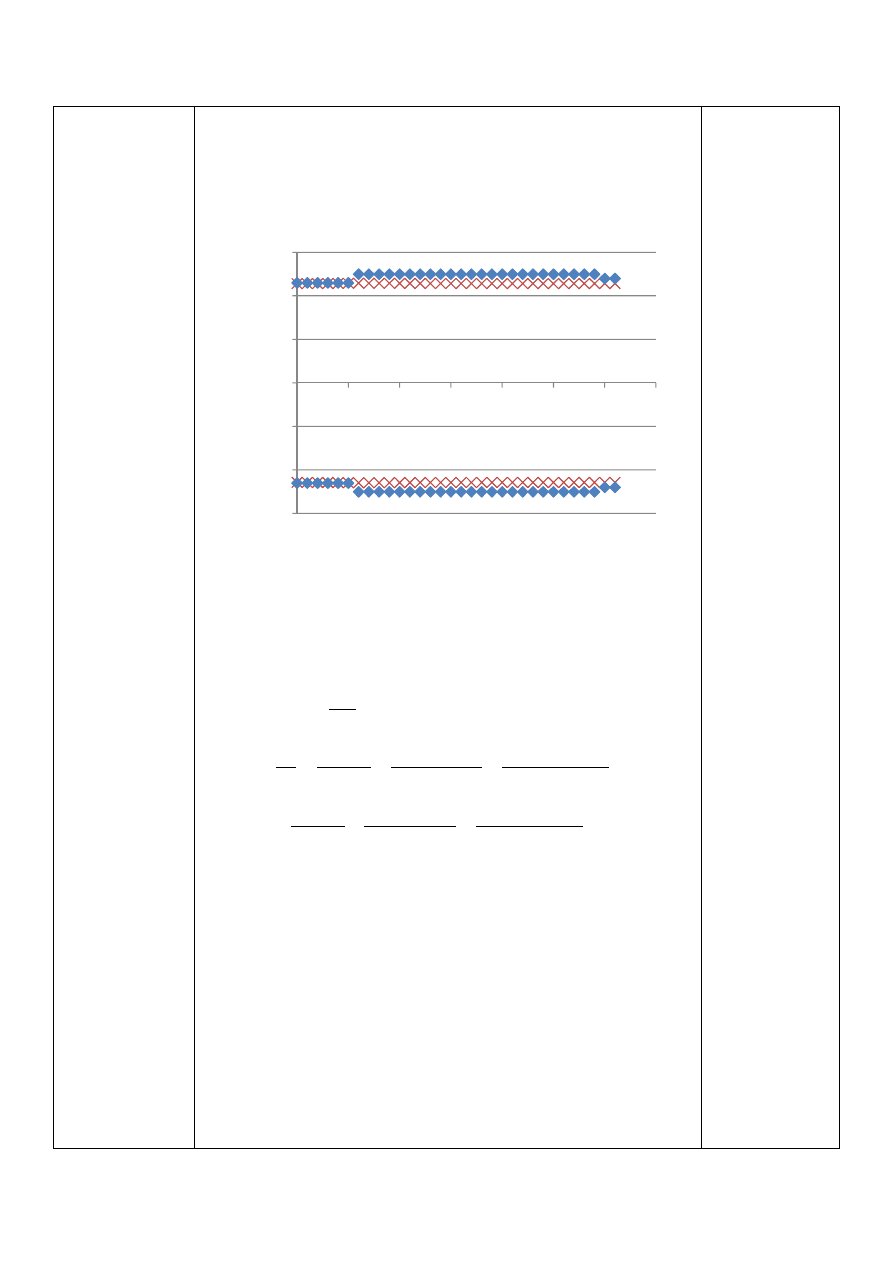
Teoretyczny zarys wału oraz zarys z dobranymi średnicami.

7.5.

Ocena sztywności giętej wału oraz sztywności skrętnej

Korzystając z metody Clebscha (płaszczyzna xy):

fª

7

h

~

7

= •

'

∙ ~ − A~ − 0,07C + •

&'

A~ − 0,19C

fª

h

~ =

•

'

∙ ~

7

2

−

A~ − 0,07C

7

2

−

•

&'

A~ − 0,19C

7

2

+ €

fªh =

•

'

∙ ~

3

6

−

A~ − 0,07C

3

6

−

•

&'

A~ − 0,19C

3

6

+ €~ + ?

Wartości C i D wyznaczane są z warunków brzegowych dla
podpór, w których:

hA0C = 0

hA0,19C = 0

Po rozwiązaniu układu równań otrzymano wartości:

€ = 135

? = 12

-60,0

-40,0

-20,0

0,0

20,0

40,0

60,0

0

50

100

150

200

250

300

350

d

,

m

m

x, mm

Zarys wału

31

Biegunowy moment bezwładności dla średnicy wału w łożyskach
d=47 mm

ª =

4

e

64 = 2,4 ∙ 10

Ir e

Moduł Younga dla stali wynosi: E=7*10

4

MPa

Maksymalne odchylenie wału:

fª

h

~ =

•

'

∙ ~

7

2

−

A~ − 0,07C

7

2

−

•

&'

A~ − 0,19C

7

2

+ €

•

'

∙ ~

7

− A~ − 0,07C

7

− •

&'

A~ − 0,19C

7

+ 2€ = 0

Rozwiązując równanie kwadratowe otrzymano:

~ = 450,1

Strzałka ugięcia:

h

'

=

•

'

∗ ~

3

6

− A~ − 0,06C

3

6

− •

&'

A~ − 0,21C

3

6

+ €~ + ?

fª

= 0,00258

Dopuszczalna strzałka ugięcia:

b

n

= A0,0005 ÷ 0,001C = 0,001 ∙ 2,75 = 0,00275

h ≤ b

n

Warunek wytrzymałościowy jest spełniony.

7.6.

Obliczenie wpustu

Zgodnie z normą PN-70/M-85005 wymiary wpustu

- × ℎ

wynoszą

14 × 9

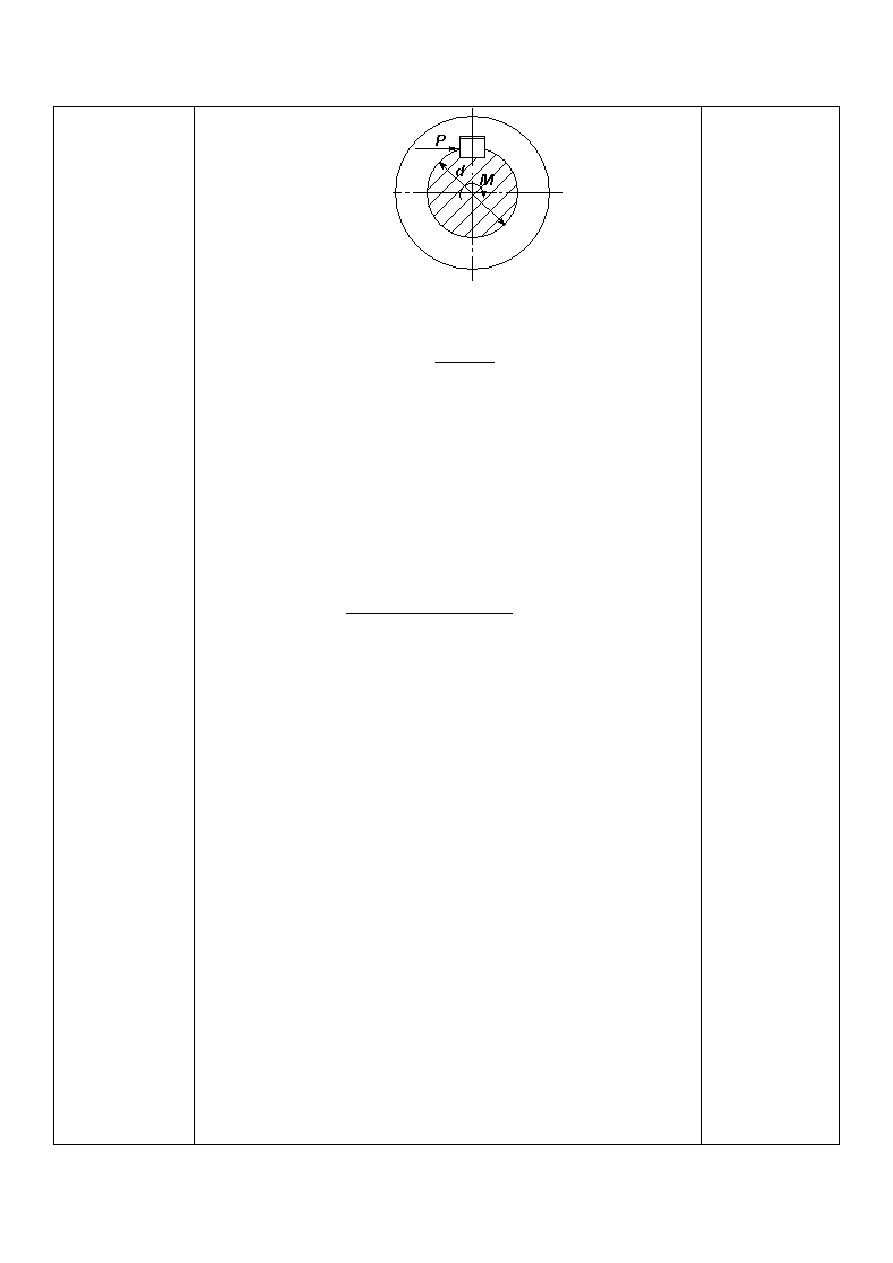
32

Długość wpustu:

<

)

≥

41

ℎ ∙ ∙

n

Dla połączeń spoczynkowych:

n

= 50 − 1201 2

Przyjęto maksymalną wartość k

d

.

Średnica wału na której osadzone jest koło:

= 47

Zatem:

<

)

≥

4 ∙ 151

0,009 ∙ 0,047 ∙ 120 ∙ 10

l

= 12

Rzeczywista długość wpustu:

< = <

)

+ - = 26

Dobieram długość wpustu 30 mm

33

L

6

= 90

L

7

= 100

L

3

= 70

%

= 43410

= 18470

@

= 13980

&

= 6627

8.

Obliczenie drugiego wału

8.1.

Wyznaczenie reakcji w podporach

•

Siły działające w płaszczyźnie xy:

Równania reakcji są następujące:

} X

'

= •

&'

−

%

+ + •

'

= 0

} X = 0

} 1 = ∙ L

3

−

%

AL

3

+ L

7

C + •

&'

AL

6

+ L

7

+ L

3

C = 0

Po przekształceniu otrzymano wartości sił w podporach:

•

&'

= 23411

•

'

= 1529

•

Siły działające w płaszczyźnie zy:

} X = •

&

−

%

+

@

+ • = 0

} X = • −

&

= 0

} 1 =

@

∙ L

3

−

&

∙

1

2

6

−

%

AL

7

+ L

3

C

+ •

&

AL

6

+ L

7

+ L

3

C = 0

•

&'

= 23411

•

'

= 1529

34

Po przekształceniu otrzymano wartości sił w podporach:

•

&

= 27118

• = 6627

• = 2312

8.2.

Obliczenie momentów gnących:

•

Płaszczyzna xy:

Dla:

0 ≤ ~ ≤ 70

1

g,'

A~C = •

'

∙ ~

1

g,'

A0C = 0

1

g,'

A70C = 107

Dla:

70

≤ ~ ≤ 170

1

g,'

A~C = •

'

∙ ~ + A~ − 70C

1

g,'

A70C = 107

1

g,'

A170C = 2107

Dla:

170

≤ ~ ≤ 260

1

g,'

A~C = •

'

∙ ~ + A~ − 70C −

%

A~ − 170C

1

g,'

A170C = 2107

1

g,'

A260C = 0

•

&

= 27118

• = 6627

• = 2312

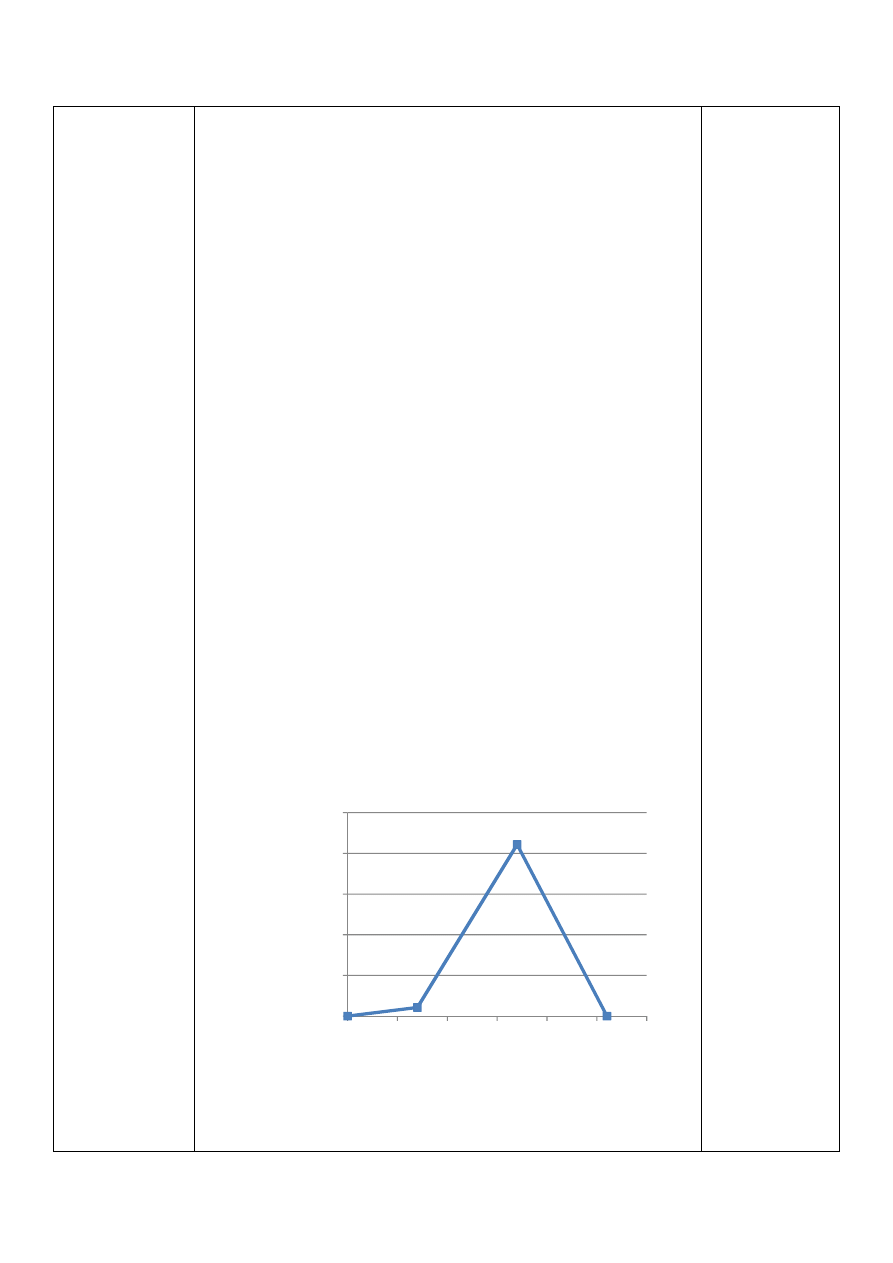
0

500

1000

1500

2000

2500

0

50

100

150

200

250

300

M

o

m

e

n

t

g

n

ąc

y

,

N

m

x, mm

Momenty gnące w płaszczyźnie xy

35

•

Płaszczyzna zy:

Dla:

0 ≤ ~ ≤ 70

1

g,

A~C = • ∙ ~

1

g,

A0C = 0

1

g,

A70C = 162

Dla:

70

≤ ~ ≤ 170

1

g,

A~C = • ∙ ~ +

@

A~ − 70C +

1

2

6

∙

&

1

g,

A70C = 380

1

g,

A170C = 2010

Dla:

170

≤ ~ ≤ 260

1

g,

A~C = • ∙ ~ +

@

A~ − 70C +

1

2

6

∙

&

−

%

A~ − 170C

1

g,

A170C = 2010

1

g,

A260C = 0

0

500

1000

1500

2000

2500

0

50

100

150

200

250

300

M

o

m

e

n

t

g

n

ąc

y

,

N

m

x, mm

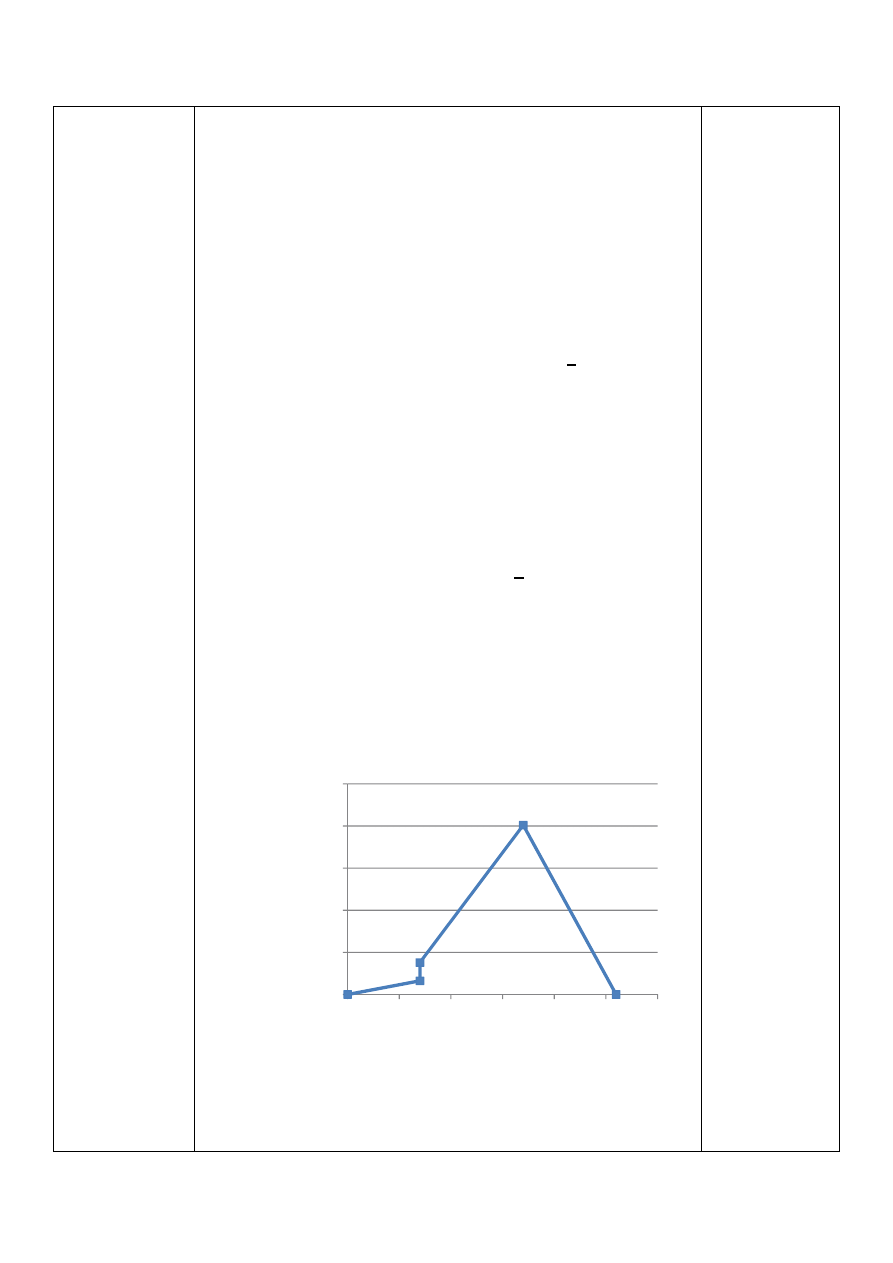
Momenty gnące w płaszczyźnie zy

36

8.3.

Obliczenie momentu zastępczego

Momenty gnące w charakterystycznych punktach wału: podpory
oraz występujące siły.

1

g6

= •1

g,' A)C

7

+ 1

g, A)C

7

= ”0

7

+ 0

7

= 0

1

g7

= •1

g,' Ar)C

7

+ 1

g, Ar)C

7

= ”107

7

+ 380

7

= 395

1

g3

= •1

g,' A6r)C

7

+ 1

g, A6r)C

7

= ”2107

7

+ 2010

7

= 2912

1

ge

= •1

g,' A7l)C

7

+ 1

g, A7l)C

7

= ”0

7

+ 0

7

= 0

0,00

500,00

1000,00

1500,00

2000,00

2500,00

3000,00

3500,00

0

50

100

150

200

250

300

M

o

m

e

n

t

g

n

ąc

y

,

N

m

x, mm

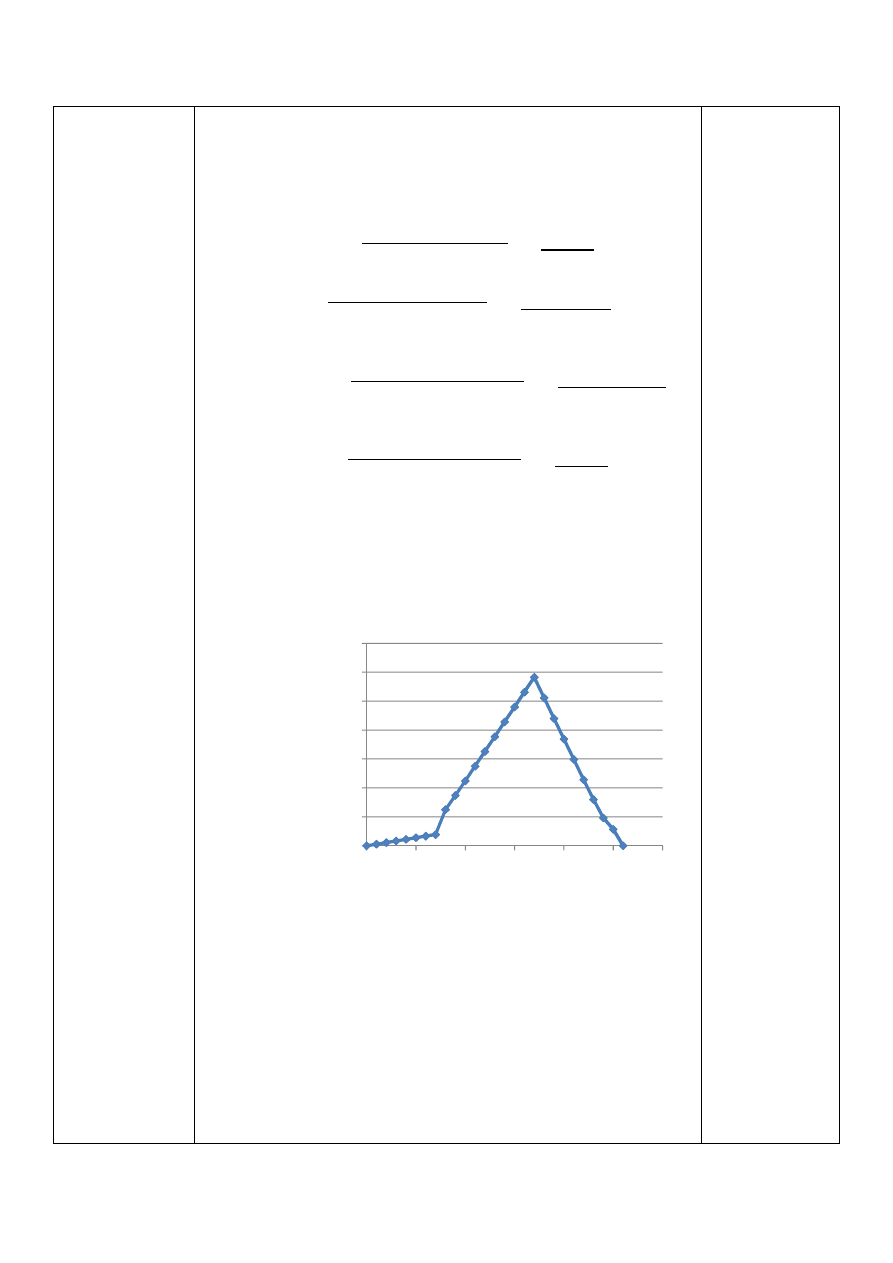
Zastępczy moment gnący

37

8.4.

Dobór średnic wału

W tabeli poniżej znajduje się zestawienie obliczonych
momentów zastępczych oraz średnic wału. Obok podano
dobraną średnicę.

Średnice wału dobrane zostały zgodnie z warunkiem:

7
6

≤ 1,2

¡, ¢¢

£

¤

, ¥¢

¦

§¨©

, ¢¢ Dobrana średnica, mm

0

6287,34

44,67

45

10

6287,41

44,67

20

6287,59

44,68

30

6287,89

44,68

40

6288,32

44,67

50

50

6288,87

44,67

60

6289,54

44,68

70

6290,34

44,68

80

6318,25

44,75

90

6347,18

44,82

100

6386,41

44,91

110

6435,74

45,03

120

6494,96

45,17

130

6563,78

45,33

140

6641,91

45,51

150

6729,03

45,72

160

6824,80

45,94

170

6928,84

46,17

180

6786,80

45,85

190

6661,02

45,56

200

6552,44

45,30

210

6461,92

45,09

220

6390,23

44,92

230

6338,00

44,79

240

6305,74

44,72

250

6293,73

43,87

45

260

6287,34

43,95

38

Teoretyczny zarys wału oraz zarys z dobranymi średnicami.

L

6

= 90

L

7

= 170

%

= 43410

9.

Obliczenia 3 wału

9.1.

Wyznaczenie reakcji w podporach

•

Siły działające w płaszczyźnie xy:

} X

'

= •

&'

+

%

+ •

'

= 0

} X = 0

} 1 =

%

∙ L

7

+ •

&'

AL

6

+ L

7

C = 0

Po przekształceniu otrzymano wartości sił w podporach:

•

&'

= 28384

•

'

= −15026

•

&'

= 28384

•

'

= −15026

-60,00

-40,00

-20,00

0,00

20,00

40,00

60,00

0

50

100

150

200

250

300

d

,

m

m

x, mm

Zarys wału

39

•

Siły działające w płaszczyźnie zy:

} X = •

&

+

%

+ • = 0

} X = • = 0

} 1 =

%

∙ L

7

+ •

&

AL

6

+ L

7

C = 0

Po przekształceniu otrzymano wartości sił w podporach:

•

&

= −28383

• = 0

• = −15026

9.2.

Obliczenie momentów gnących:

•

Płaszczyzna xy:

Dla:

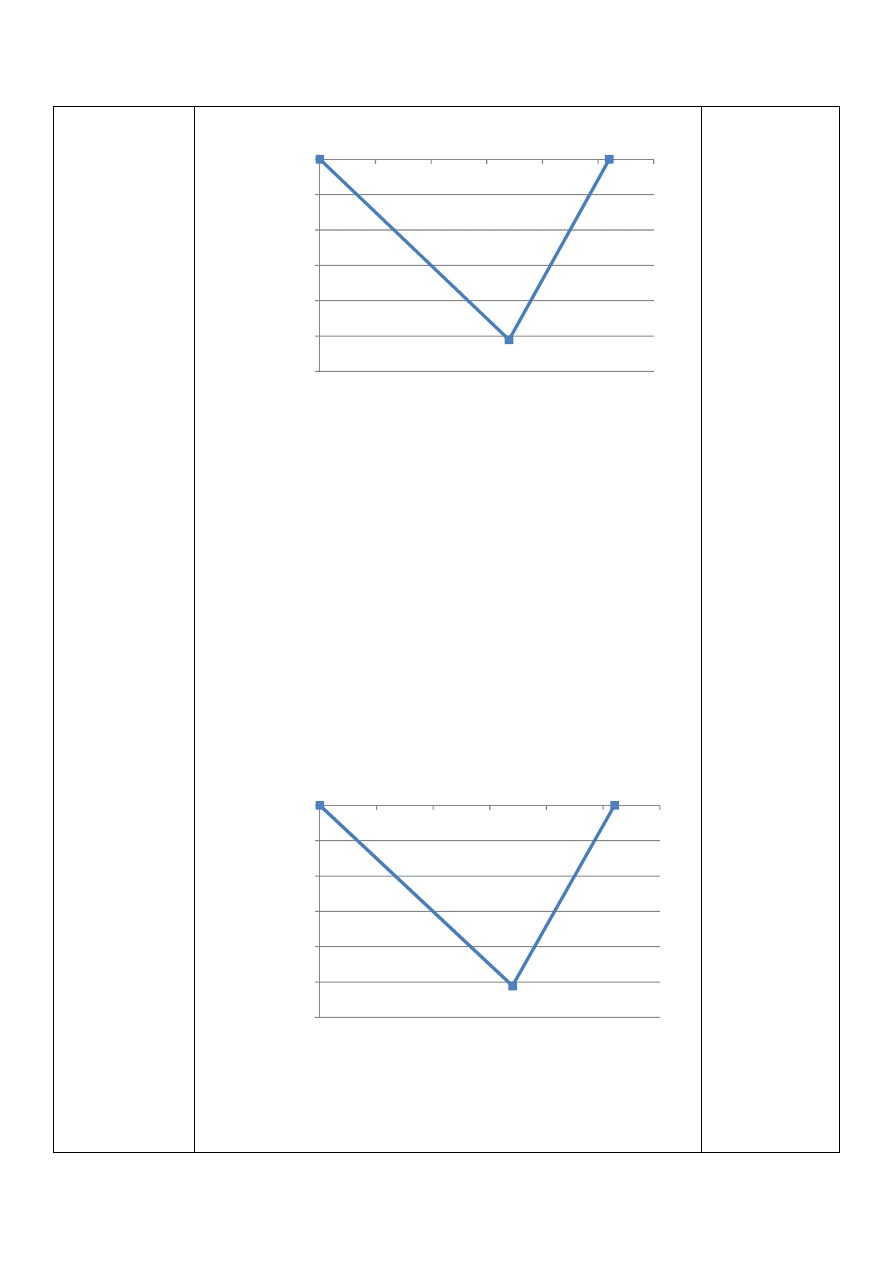
0 ≤ ~ ≤ 170

1

g,'

A~C = •

'

∙ ~

1

g,'

A0C = 0

1

g,'

A170C = −2554

Dla:

170

≤ ~ ≤ 260

1

g,'

A~C = •

'

∙ ~ +

%

A~ − 170C

1

g,'

A170C = −2554

1

g,'

A260C = 0

•

&

= −28383

• = 0

• = −15026

40

•

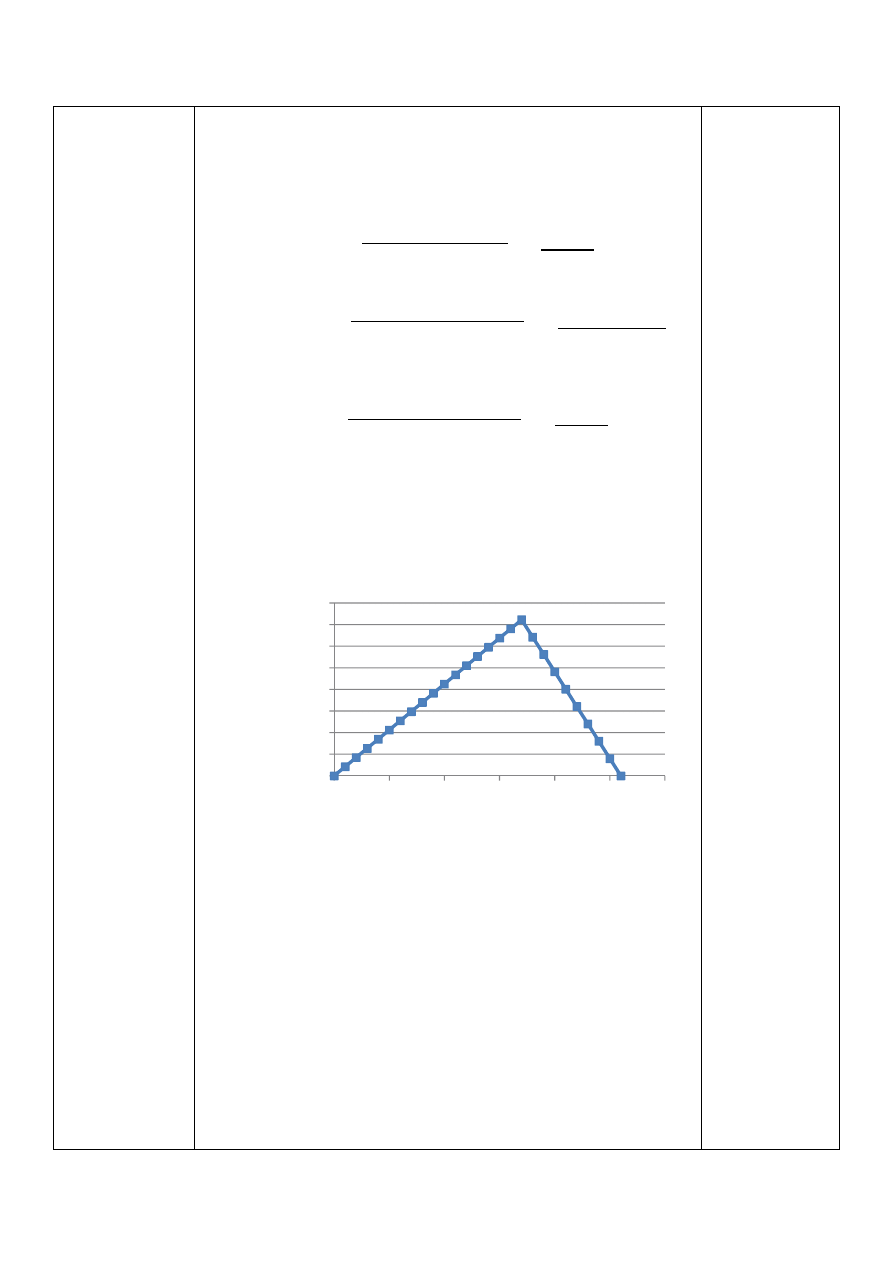
Płaszczyzna zy:

Dla:

0 ≤ ~ ≤ 170

1

g,

A~C = • ∙ ~

1

g,

A0C = 0

1

g,

A170C = −2554

Dla:

170

≤ ~ ≤ 260

1

g,

A~C = • ∙ ~ +

%

A~ − 170C

1

g,

A170C = −2554

1

g,

A260C = 0

-3000

-2500

-2000

-1500

-1000

-500

0

0

50

100

150

200

250

300

M

o

m

e

n

t

g

n

ąc

y

,

N

m

x, mm

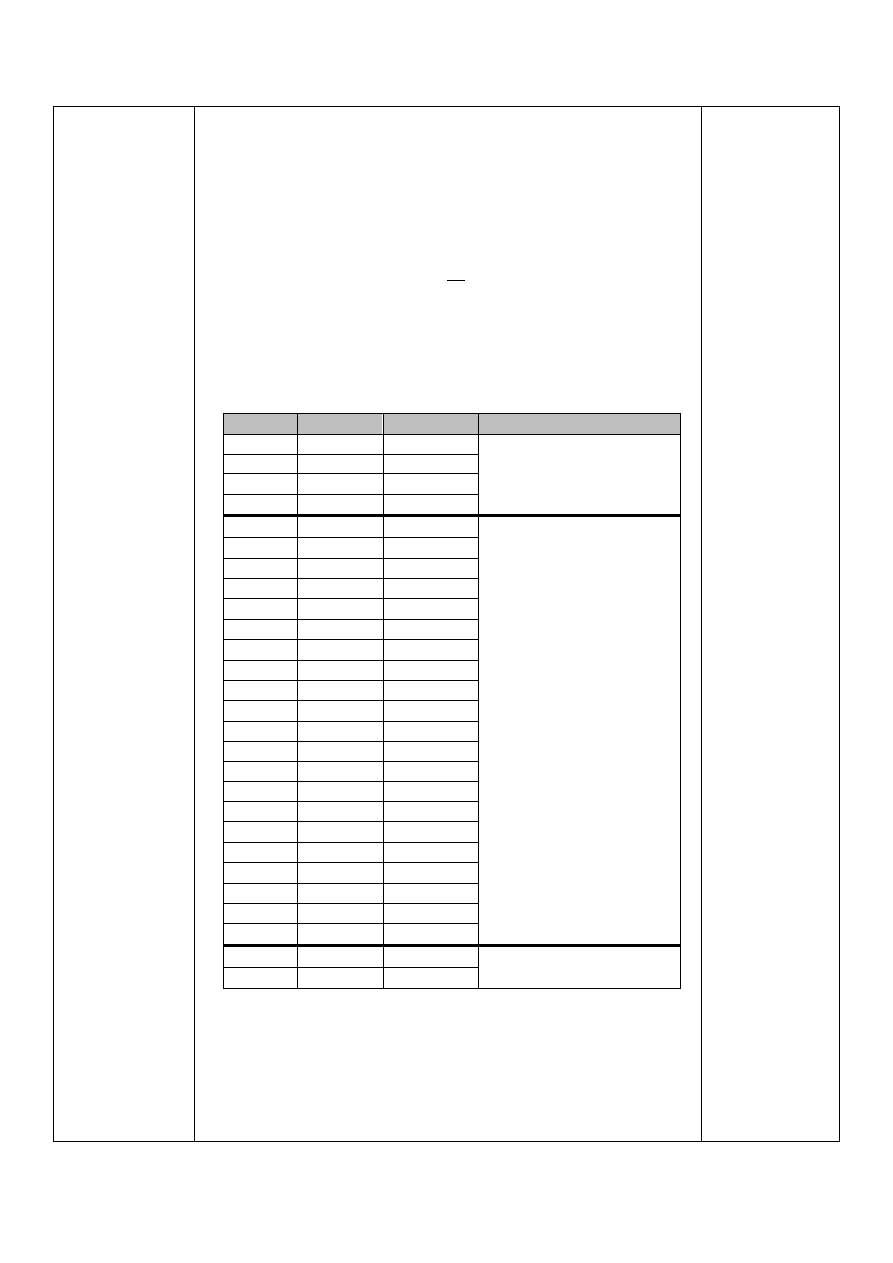
Momenty gnące w płaszczyźnie xy

-3000

-2500

-2000

-1500

-1000

-500

0

0

50

100

150

200

250

300

M

o

m

e

n

t

g

n

ąc

y

,

N

m

x, mm

Momenty gnące w płaszczyźnie zy

41

9.3.

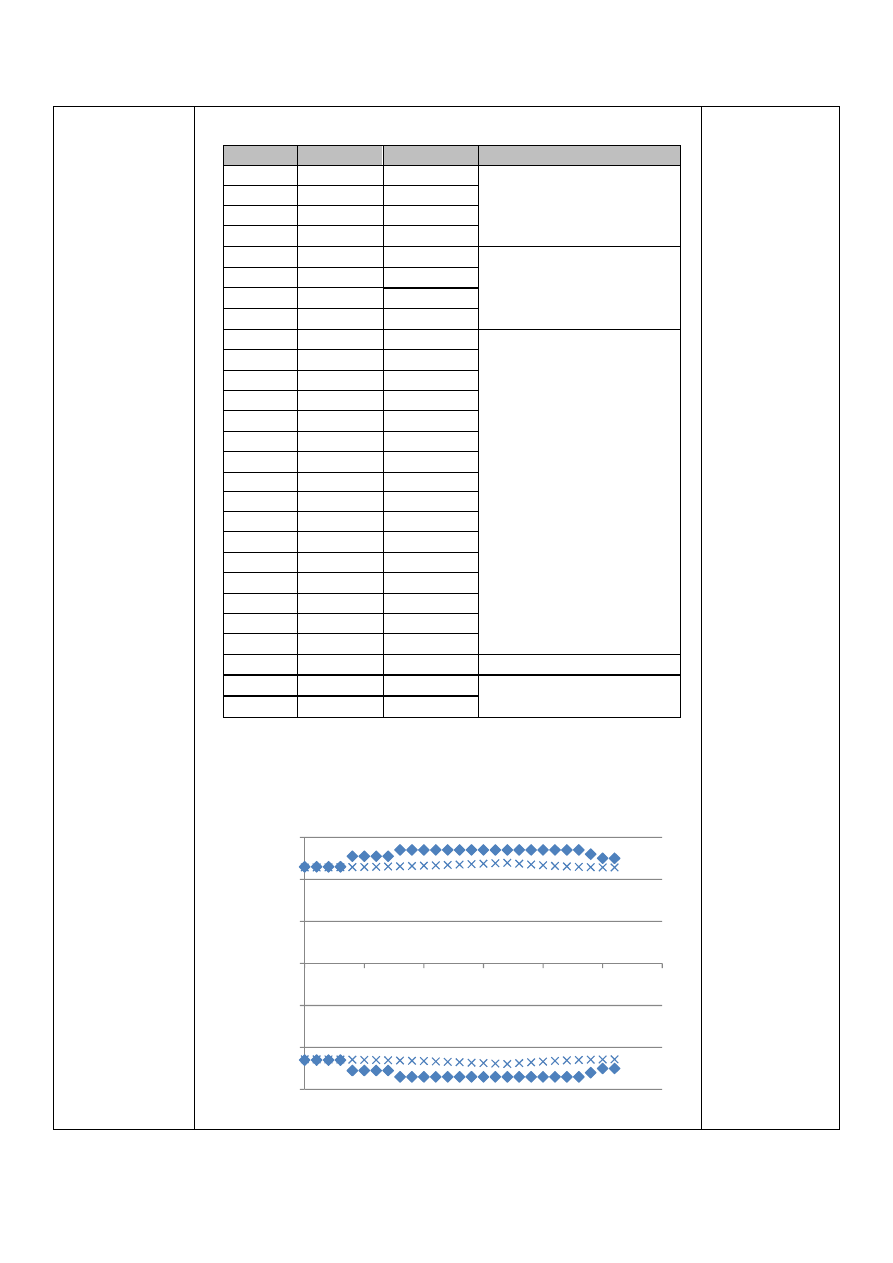
Obliczenie momentu zastępczego

Momenty gnące w charakterystycznych punktach wału: podpory
oraz występujące siły.

1

g6

= •1

g,' A)C

7

+ 1

g, A)C

7

= ”0

7

+ 0

7

= 0

1

g7

= •1

g,' A6r)C

7

+ 1

g, A6r)C

7

= ”2554

7

+ 2554

7

= 3612

1

g3

= •1

g,' A7l)C

7

+ 1

g, A7l)C

7

= ”0

7

+ 0

7

= 0

0,00

500,00

1000,00

1500,00

2000,00

2500,00

3000,00

3500,00

4000,00

0

50

100

150

200

250

300

M

o

m

e

n

t

g

n

ąc

y

,

N

m

x, mm

Zastępczy moment gnący

42

¡, ¢¢

£

¤

, ¥¢

¦

§¨©

, ¢¢ Dobrana średnica, mm

0

6287,34

44,67

45

10

6290,93

44,68

20

6301,69

44,71

30

6319,58

44,75

40

6344,54

4,81

51

50

6376,49

44,89

60

6415,32

44,98

70

6460,91

45,09

80

6513,12

45,21

54

90

6571,78

45,35

100

6636,74

45,50

110

6707,80

45,67

120

6784,78

45,85

130

6867,47

46,03

140

6955,67

46,24

150

7049,17

46,45

160

7147,77

46,67

170

7251,26

46,89

180

7059,87

46,47

190

6886,58

46,08

200

6732,79

47,73

210

6599,86

47,42

220

6489,08

45,15

230

6401,59

44,95

240

6338,37

44,79

52

250

6300,13

44,70

50

260

6287,34

44,67

-60,00

-40,00

-20,00

0,00

20,00

40,00

60,00

0

50

100

150

200

250

300

d

,

m

m

x, mm

Zarys wału

43

Po przeprowadzeniu wszystkich obliczeń wyznaczono wszystkie niezbędne wartości do

wykonania dwustopniowego reduktora walcowego. Rysunek złożeniowy urządzenia oraz rysunki
wykonawcze wybranych elementów znajdują się w załączniku do projektu.

Literatura:

[1] Leonid W. Kurmaz, Oleg L. Kurmaz, „Podstawy konstruowania węzłów i części maszyn”

[2] E. Mazanek, „Przykłady obliczeń z podstaw konstrukcji maszyn. Tom 2”