O PROMIENIACH ŚWIETLNYCH, ICH ODBICIU I ZAŁAMANIU
Dr inż. Marek Zając
Pracownia Optyki Widzenia
Instytut Fizyki Politechniki Wrocławskiej,
e-mail:
zajac@if.pwr.wroc.pl
(Opublikowane w Ogólnopolskim Kurierze Oftalmicznym "OKO", nr 4/ 2000)
Czym jest światło? Na czym polega widzenie? Jak działa oko? Takie i podobne pytania
nurtowały ludzi już od początku historii. Różnie próbowano na nie odpowiadać. Niektóre
wyjaśnienia były dość naiwne - na przykład hipoteza, że oko wysuwa przed siebie jakby czułki,
które "obmacują" otoczenie i dostarczają informacji o pobliskich przedmiotach. Taka myśl
wydaje się nam dziś niemądra i dziecinna. Jednak nie dziwmy się ówczesnym ludziom -
jesteśmy od nich starsi i mądrzejsi o ładnych kilka tysięcy lat.
Obserwacja otaczającej nas przyrody, np. smug światła przedzierających się miedzy liśćmi
drzewa w słoneczny dzień, doprowadziła do stworzenia najważniejszego pojęcia optyki
geometrycznej, jakim jest promień światła. Mówiąc o promieniu światła myślimy dziś o linii,
wzdłuż której rozchodzi się energia świetlna - w rzeczywistości, lub tylko potencjalnie (jest to
więc możliwy kierunek rozchodzenia się energii). Pojęcie promienia jest utożsamiane z linią
geometryczną, dlatego początkowo optyka była częścią geometrii. W geometrii Euklidesa
znajdujemy podstawowe prawa optyki geometrycznej: prawo prostoliniowego rozchodzenie się
światła oraz prawo odbicia.
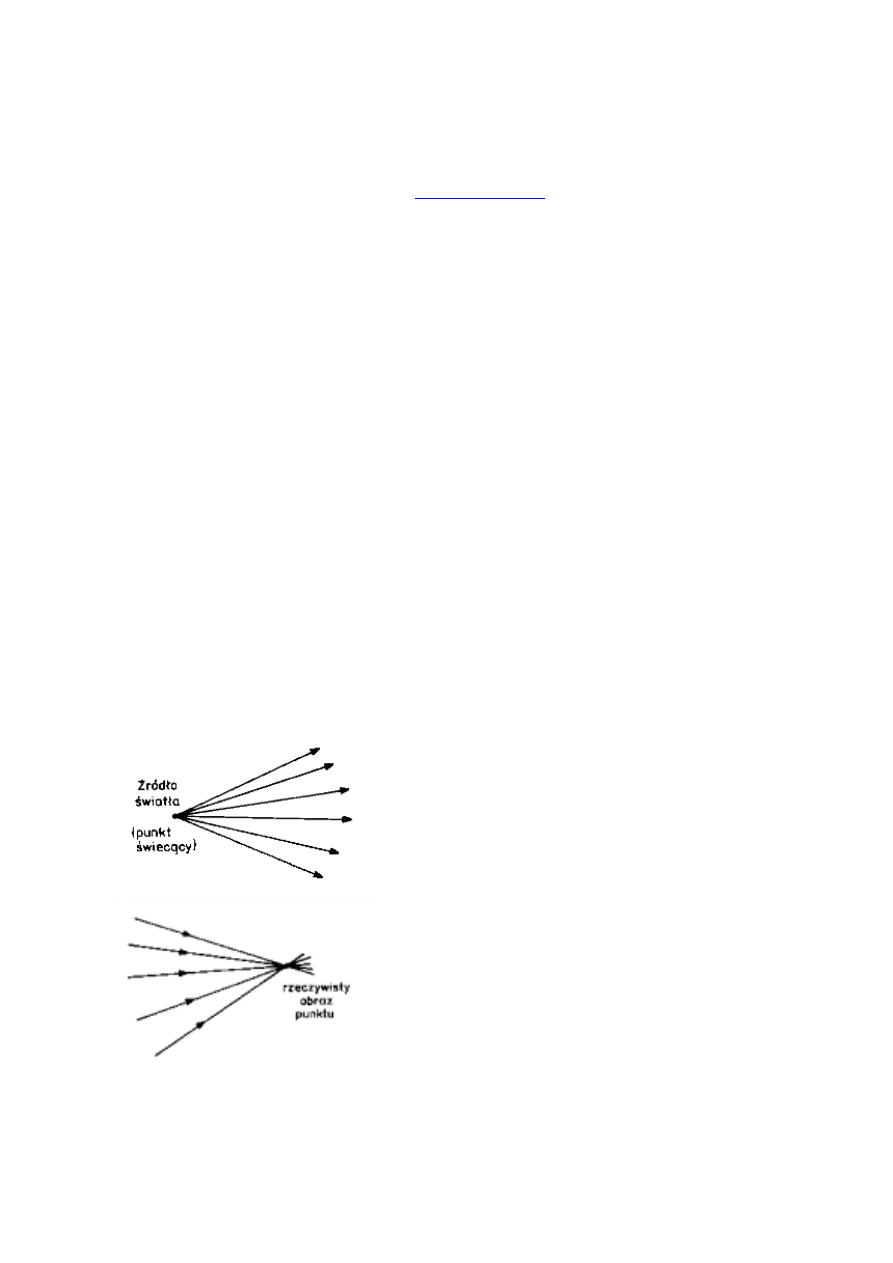
Najbardziej oczywistym wydaje się prawo prostoliniowego rozchodzenia się światła. Potwierdza
je codzienna obserwacja: Promienie świetlne wychodzą ze źródła światła i rozbiegają się wzdłuż
linii prostych aż natrafią na przeszkodę lub znikną w nieskończoności. Wyobrażamy sobie, że
promienie świetlne jakby niosą ze sobą energię. Im więc gęściej przebiegają, tym bardziej
skoncentrowana energia świetlna. Punkt, z którego promienie się rozbiegają to punktowy
przedmiot świecący (rysunek 1), a w miejscu, gdzie się z powrotem zbiegają, powstaje jego
rzeczywisty obraz (rysunek 2). Może tak się zdarzyć, że w pewnym obszarze nie przecinają się
promienie świetlne, ale ich przedłużenia. Wyobrażamy sobie wtedy, że ten punkt jest pozornym
przedmiotem czy obrazem (rysunek 3).
Rys. 1
Punktowe źródło światła
Rys. 2
Rzeczywisty obraz świecącego punktu
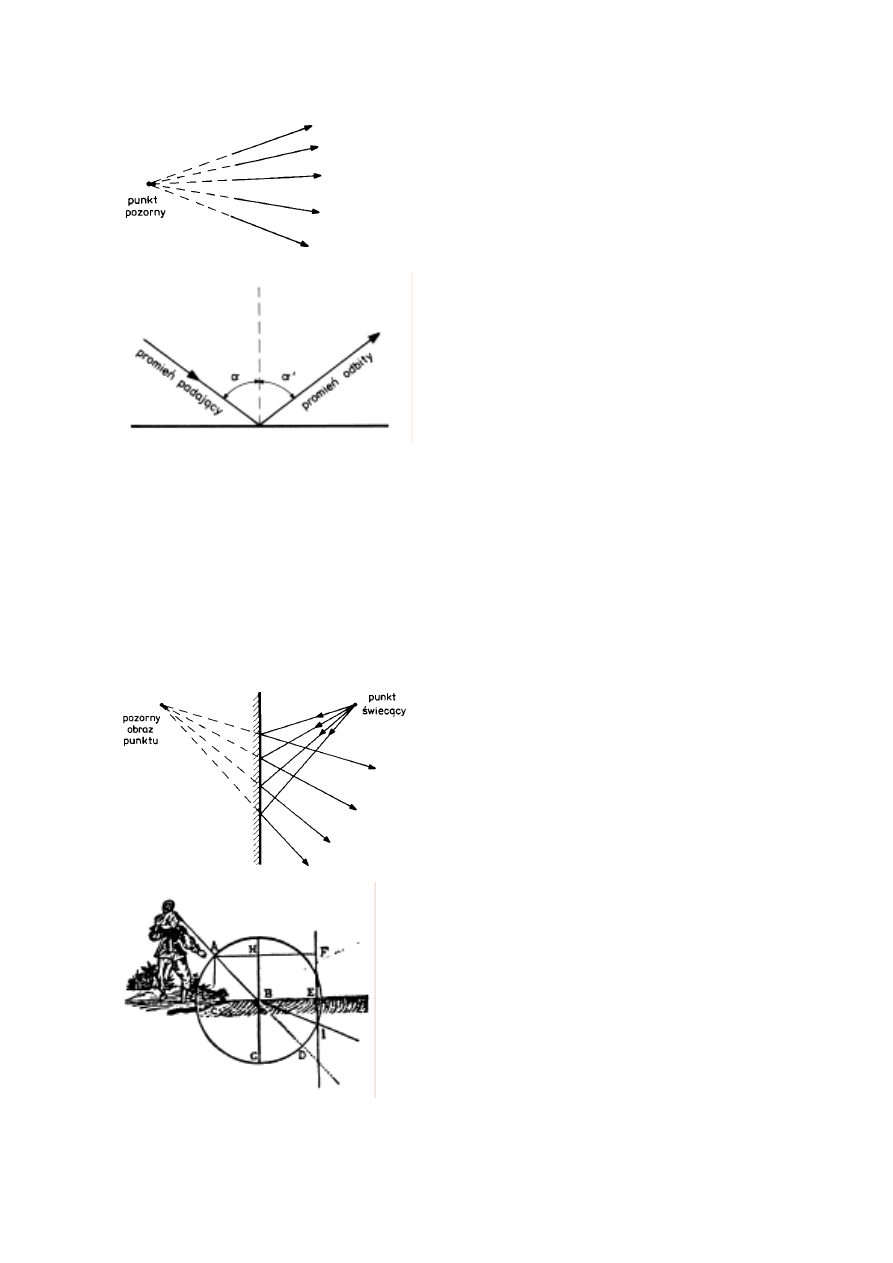
Rys. 3
Pozorny obraz świecącego punktu
Rys. 4.
Prawo odbicia światła
Światło natrafiające na przeszkodę może się od niej odbić. Jeśli powierzchnia przeszkody jest
gładka, to mamy do czynienia z odbiciem lustrzanym. Prawo odbicia, znane już Archimedesowi,
stwierdza, że oba promienie, padający i odbity, leżą w jednej płaszczyźnie, zaś kąt między
kierunkiem promienia odbitego a prostopadłą do powierzchni odbijającej jest równy kątowi
między kierunkiem promienia padającego a tą samą prostopadłą i to niezależnie od wielkości
tego kąta (rysunek 4). To prawo, choć tak proste i oczywiste, jest ważnym narzędziem w rękach
optyka. Pozwala bowiem wyjaśnić zasadę tworzenia obrazów w lustrach (rysunek 5) i
projektować rozmaite zwierciadlane układy lustrzane, nawet tak bardzo skomplikowane, jak
wielkie teleskopy astronomiczne.
Rys. 5
Pozorny obraz punktu widziany w zwierciadle płaskim
Rys. 6
Rysunek z pracy Newtona wyjaśniający (błędnie) prawo
załamania
Rys. 7
Rysunek ze strony tytułowej norymberskiego wydania
dzieła Witelona "Perspectiva"
Drugie prawo dotyczące zachowania się promieni świetlnych na granicy dwóch ośrodków
przezroczystych jest znacznie młodsze. Przez wiele lat nie potrafiono go poprawnie sformułować
(por. rysunek 6). Wydaje się, że rozumiał je pochodzący z Legnicy wielki polski uczony
Średniowiecza, Witelo (rysunek 6 przedstawia fragment okładki jego dzieła "Perspectiva"), ale
ostateczne sformułowanie tego prawa wiąże się dopiero z nazwiskiem niderlandzkiego uczonego
z XVII w Willibrorda Snella. Prawo załamania, o którym mowa, stwierdza, że promień
załamany i padający leżą także w jednej płaszczyźnie, ale kąt między promieniem załamanym a
prostopadłą nie jest wcale równy kątowi między promieniem padającym a normalną, ba, nie są
one nawet proporcjonalne. Zmiana kąta padania o pewną wartość pociąga za sobą
nieproporcjonalną zmianę kąta załamania. Okazuje się, że przy zmienianiu kierunku promienia
padającego w stałej proporcji pozostają sinusy tych kątów. Stosunek między sinusem kąta
załamania a sinusem kąta padania charakteryzuje właściwości optyczne obu ośrodków, na
których granicy następuje załamanie, i nazywa się względnym współczynnikiem załamania
światła ośrodka, do którego światło wchodzi względem ośrodka, z którego światło pada
. (
W
środowisku optyków okularowych słyszy się często określenie "indeks". Jest to oczywista,
nieudolna kalka z języka angielskiego -"index of refraction". Ponadto słowo "indeks" ma wiele
innych znaczeń. Wobec istnienia właściwego, poprawnego terminu polskiego nie powinno się go
więc używać.
)
Matematycznie prawo załamania formułuje się następująco (oznaczenia są
objaśnione na rysunku 8):
(1)
Rys. 8
Ilustracja prawa załamania
Wymienione dwa podstawowe prawa optyki geometrycznej, wraz z trygonometrią, szczyptą
wyobraźni przestrzennej i sporą dawką cierpliwości oraz pracowitości pozwalają projektować
lupy, lunety, mikroskopy, aparaty fotograficzne i rozmaite inne przyrządy optyczne - także
soczewki okularowe.
Człowiek zawsze chciałby znaleźć wytłumaczenie odkrywanych przez siebie praw, choćby tak
prostych jak prawo odbicia czy załamania światła. Zapytajmy więc, jak to się dzieje, że promień
światła odbija się zawsze pod takim samym kątem jak pada, a przy załamaniu kierunek
promienia rozchodzącego się w drugim ośrodku określony jest formułą (1). Otóż w wielu
zjawiskach fizycznych obowiązuje tzw. zasada Fermata. W przypadku rozchodzenia się światła
mówi ona, że droga światła jest taka, by jej przejście wymagało najkrótszego czasu (czyżby ta
zasada kierowała także naszym postępowaniem w codziennym życiu?). Czas ten zależy
oczywiście od prędkości, z jaką rozchodzi się światło. W ośrodku jednorodnym takim jak:
powietrze, woda czy szkło jest ona taka sama, niezależnie od miejsca czy kierunku (Ściśle biorąc
jest to założenie o izotropowości i jednorodności tych ośrodków. Czasem jest inaczej, ale w tym
momencie nie będziemy zajmować się odstępstwami od tego założenia). Jeśli tak jest, to na to,
aby w najkrótszym czasie pokonać odległość między dwoma punktami trzeba poruszać się po
łączącej je linii prostej. I mamy prawo prostoliniowego rozchodzenia się światła!
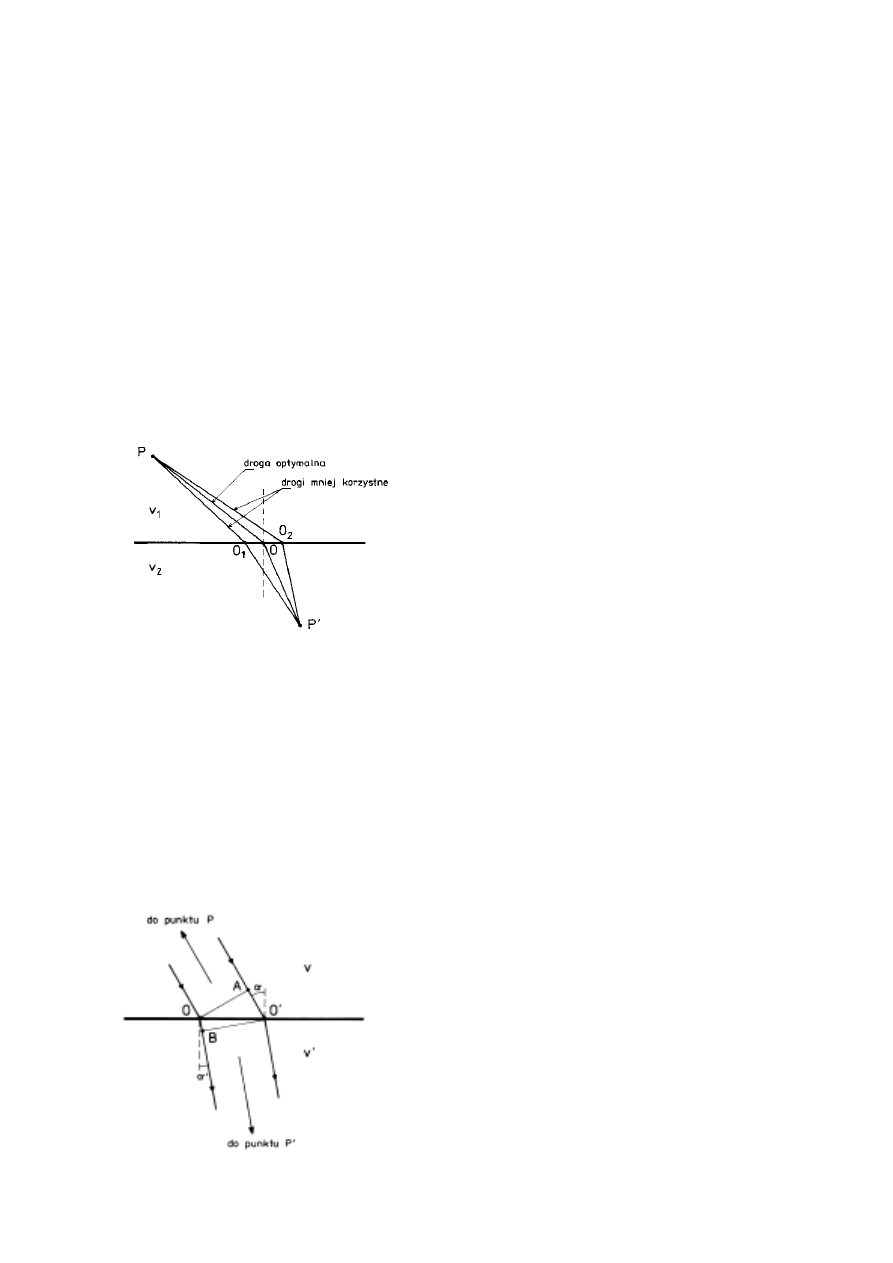
Rys. 9
Zasada Fermata
Nietrudno przekonać się, że jeśli założymy, iż światło ma dotrzeć od jednego punktu do
drugiego odbijając się po drodze od lustrzanej powierzchni to odpowiednie kąty padania
i odbicia muszą być sobie równe. Tak mówi prawo odbicia. Droga POP' na rysunku 9 jest
krótsza od dróg PO
1
P' i PO
2
P'.
Prawo załamania także wynika z zasady Fermata. Łatwo zrozumieć, że droga światła
przechodzącego przez dwa różne ośrodki będzie zależała od prędkości, z jaką owo światło się
w nich rozchodzi. Aby wypadkowy czas był najkrótszy, długość drogi w ośrodku, w którym
prędkość jest mniejsza, musi być krótsza od długości drogi w ośrodku, w którym światło porusza
się szybciej. W rezultacie światło biegnie po takiej linii, by wypadkowy czas był najkrótszy
spośród możliwych.
Rys. 10
Wyprowadzenie prawa załamania z zasady Fermata
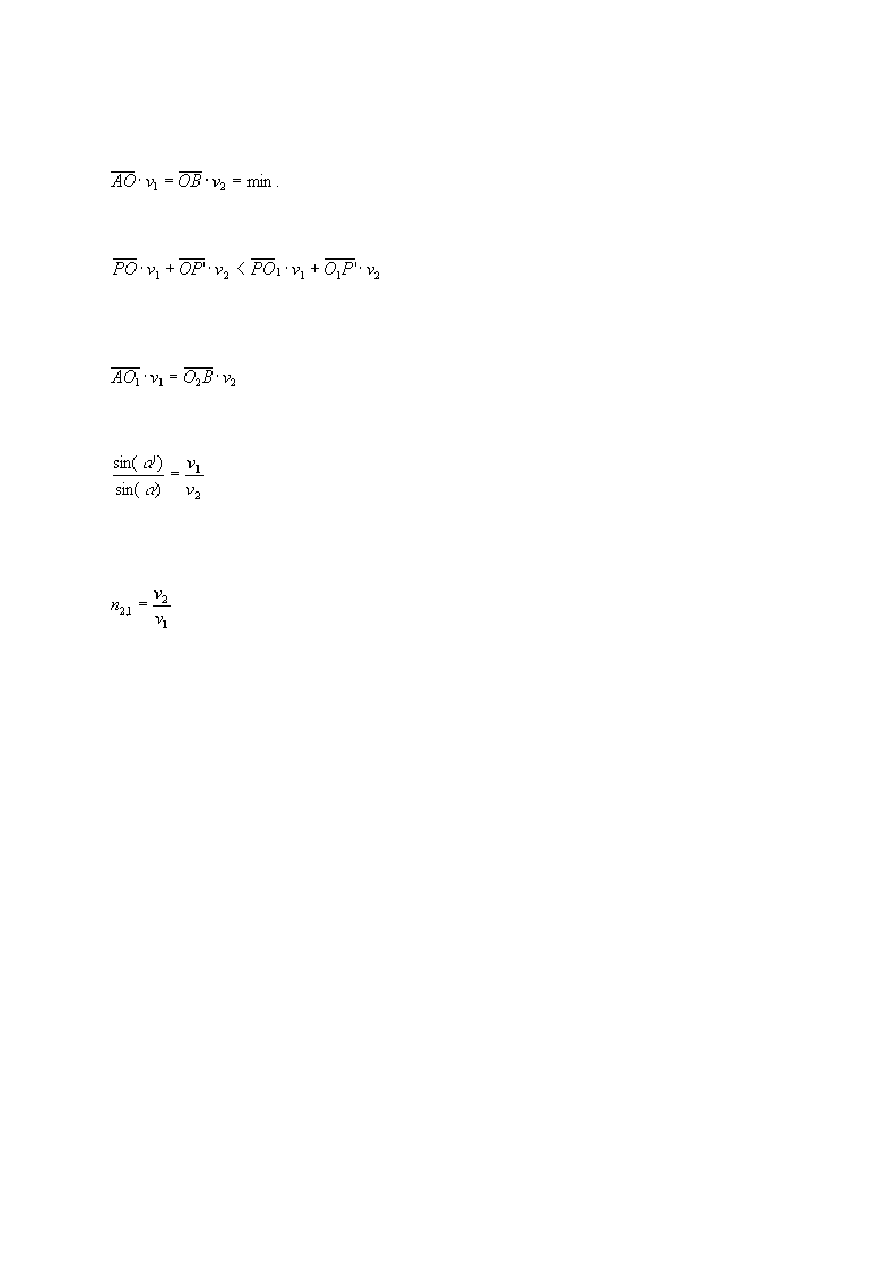
Matematycznie można to wyrazić następująco:
(2)
Inaczej można to wyrazić nierównością:
(3)
Pomagając sobie rysunkiem 10, można sprawdzić, że droga światła jest najkorzystniejsza wtedy,
kiedy spełnione jest równanie:
(4)
z czego wynika proporcja:
(5)
Ta proporcja jest właśnie dokładnym prawem załamania, a współczynnik załamania ośrodka
względem otoczenia jest równy stosunkowi prędkości światła w otoczeniu i w ośrodku:
(6)
Jak powszechnie wiadomo bardzo dobrze zmierzoną wielkością jest prędkość światła w próżni,
wynosząca niemal 300 000 km/s. W powietrzu światło rozchodzi się z prawie taka samą
prędkością. Dlatego wygodnie posługiwać się współczynnikiem załamania materiału
teoretycznie względem próżni (określa się go mianem bezwzględnego współczynnika
załamania), a w praktyce względem powietrza. Opisujemy nim załamanie światła na granicy
między powietrzem a np. szkłem.
Typowa wartość bezwzględnego współczynnika załamania szkła wynosi około n = 1,5 co
oznacza, że prędkość światła w szkle jest 1,5 razy mniejsza niż w próżni. W wodzie światło
porusza się około 25% wolniej niż w próżni, co daje wartość współczynnika załamania wody
n = 1,33.
Skąd się bierze zasada Fermata? Na to pytanie nie da się już odpowiedzieć tak łatwo, można
sobie jednak wyobrazić pewną ilustrację. Przypuśćmy, że grupka dzieci trzymających się za ręce
wędruje przez drogi i pola. Jak długo maszerują wszyscy po takim samym terenie, każde porusza
się z taką sama prędkością i idą obok siebie. Z chwilą, gdy napotykają na inne podłoże (np.
schodzą z drogi na pole) prędkość wędrówki poszczególnych dzieci ulega zróżnicowaniu.
Prędkość marszu tych, którzy są jeszcze na drodze, nie zmienia się, ale tych, którzy już zeszli na
łąkę - maleje. Jedni wysuwają się więc do przodu, inni pozostają w tyle. Aby móc nadal iść obok
siebie i trzymać się za ręce muszą zakręcić tak, aby ci, którzy idą wolniej, mieli do przebycia
krótszą drogę od idących szybciej. W rezultacie wybierają taką drogę, by każdemu z nich
zabierała tyle samo czasu. Matematycznym wyrazem takiego zachowania jest właśnie zasada
Fermata.
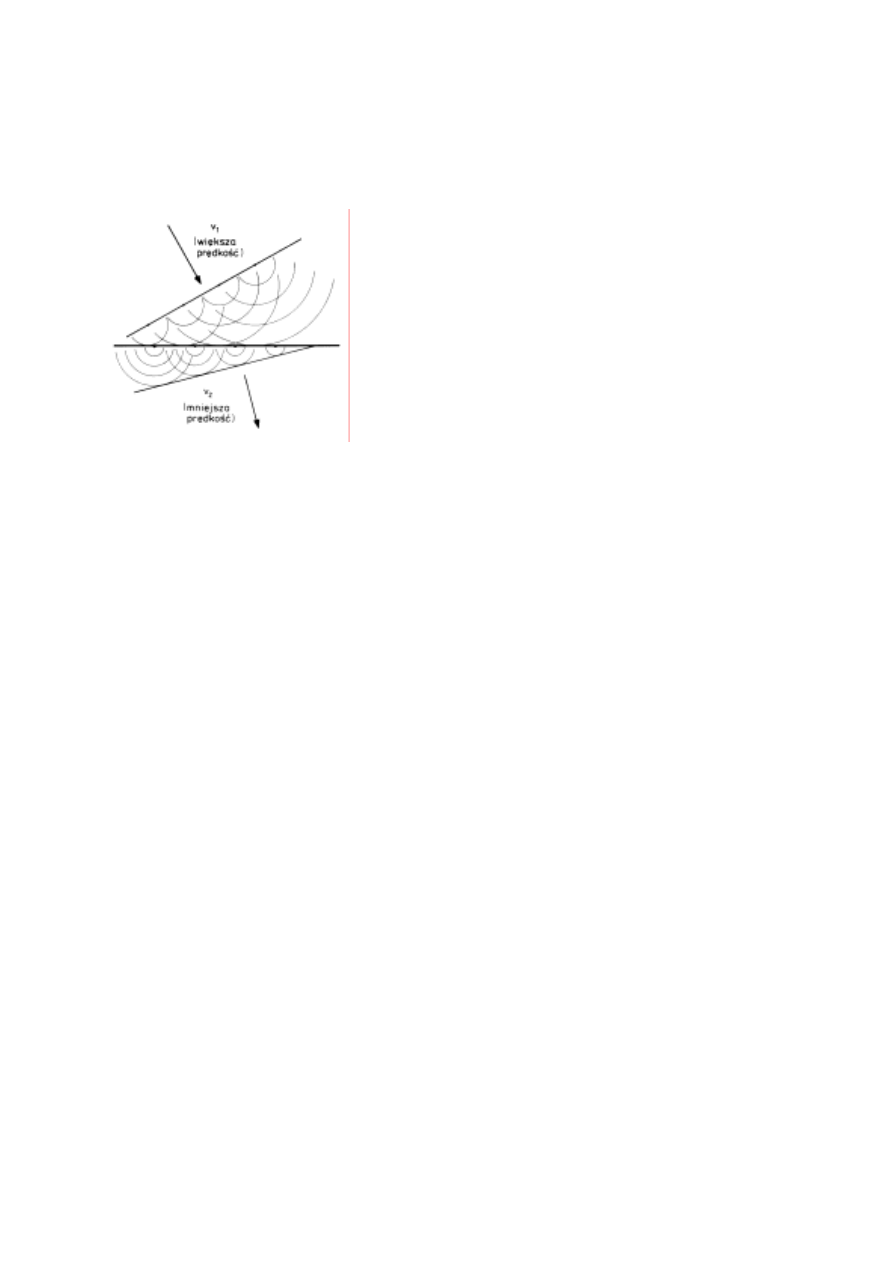
Inne wytłumaczenie praw odbicia i załamania daje zasada Huygensa. Jeśli światło traktować
jako falę to za Christiaanem Huygensem możemy sformułować zasadę mówiącą, iż każdy punkt
do którego fala dochodzi, staje się źródłem nowej fali kulistej. Po pewnym (niesłychanie
krótkim) czasie każda z takich elementarnych fal rozprzestrzeni się na odległość odwrotnie
proporcjonalną do szybkości rozchodzenia się w danym ośrodku. Wypadkowa fala biegnie w
kierunku prostopadłym do linii łączącej "skraje", czyli "czoła" takich elementarnych fal. Jak
widać z konstrukcji przedstawionej na rysunku 11 wyjaśnia to zmianę kierunku fali na granicy
dwóch ośrodków i to dokładnie według formuły (6).
Rys. 11
Wyprowadzenie prawa załamania z zasady Huygensa
Na koniec warto zapytać, czy nigdy nie zdarzają się odstępstwa od prawa prostoliniowego
rozchodzenia się światła. Otóż oczywiście, że tak.
Zasada Fermata podpowiada, że droga światła, najszybsza w danych warunkach, zależy od
prędkości rozchodzenia się światła. Od tej prędkości, jak pamiętamy, zależy współczynnik
załamania. Zasadę Fermata można więc sformułować inaczej, posługując się pojęciem drogi
optycznej. Jest to po prostu iloczyn rzeczywistej drogi geometrycznej i lokalnego współczynnika
załamania. Bieg światła jest taki, by droga optyczna była najkrótsza. Jeśli współczynnik
załamania różnych obszarów ośrodka jest różny, to światło "wybiera" taką trajektorię, by
możliwie skrócić drogę w ośrodku o większym współczynniku załamania (tzw. ośrodku
optycznej gęściejszym) kosztem wydłużenia drogi w ośrodku o mniejszym współczynniku
załamania (czyli optycznie rzadszym). Kiedy mamy do czynienia z takim niejednorodnym
ośrodkiem? Wystarczy pomyśleć o szklance herbaty, do której wrzucono kostkę cukru. Jeśli nie
będziemy mieszali herbaty, to rozpuszczający się cukier zgromadzi się na dnie szklanki. Okazuje
się przy tym, że prędkość rozchodzenia się światła w słodkiej herbacie jest inna niż w gorzkiej.
Promień światła przechodzący przez szklankę nie rozmieszanej herbaty nie biegnie po linii
prostej!
Podobna sytuacja ma miejsce w bloku szkła odlanego z niedobrze rozmieszanej masy
szklarskiej. Wewnątrz kawałka szkła mogą znaleźć się obszary o współczynniku załamania
odmiennym niż w reszcie bloku, tzw. smugi. Smużystość jest wadą dyskwalifikującą szkło jako
surowiec do wykonywania soczewek czy innych elementów optycznych.
Niejednorodność współczynnika załamania może wynikać nie tylko z różnic składu
chemicznego materiału. Często spotykaną przyczyną są różnice temperatur. Wyobraźmy sobie
powietrze nad rozgrzaną asfaltową szosą. Tuż nad jej powierzchnią jest cieplejsze i ma mniejszy
współczynnik załamania niż nieco wyżej. Nad taką rozgrzaną szosą światło biegnie po liniach
zakrzywionych. Obrazy odległych przedmiotów wydają się znajdować w innych miejscach niż
są w rzeczywistości. Patrzymy na szosę i widzimy jakby kałuże wody, podjeżdżamy bliżej -
szosa jest sucha. To nie kałuże, ale obraz nieba widziany dzięki zjawisku mirażu. Na rysunku 12
widać bieg promieni świetlnych odpowiedzialny za to złudzenie. Zjawisko mirażu, czyli
fatamorgany zdarza się przy bardzo dużych różnicach temperatur. Obrazy są przy tym często
zamazane i drgające.
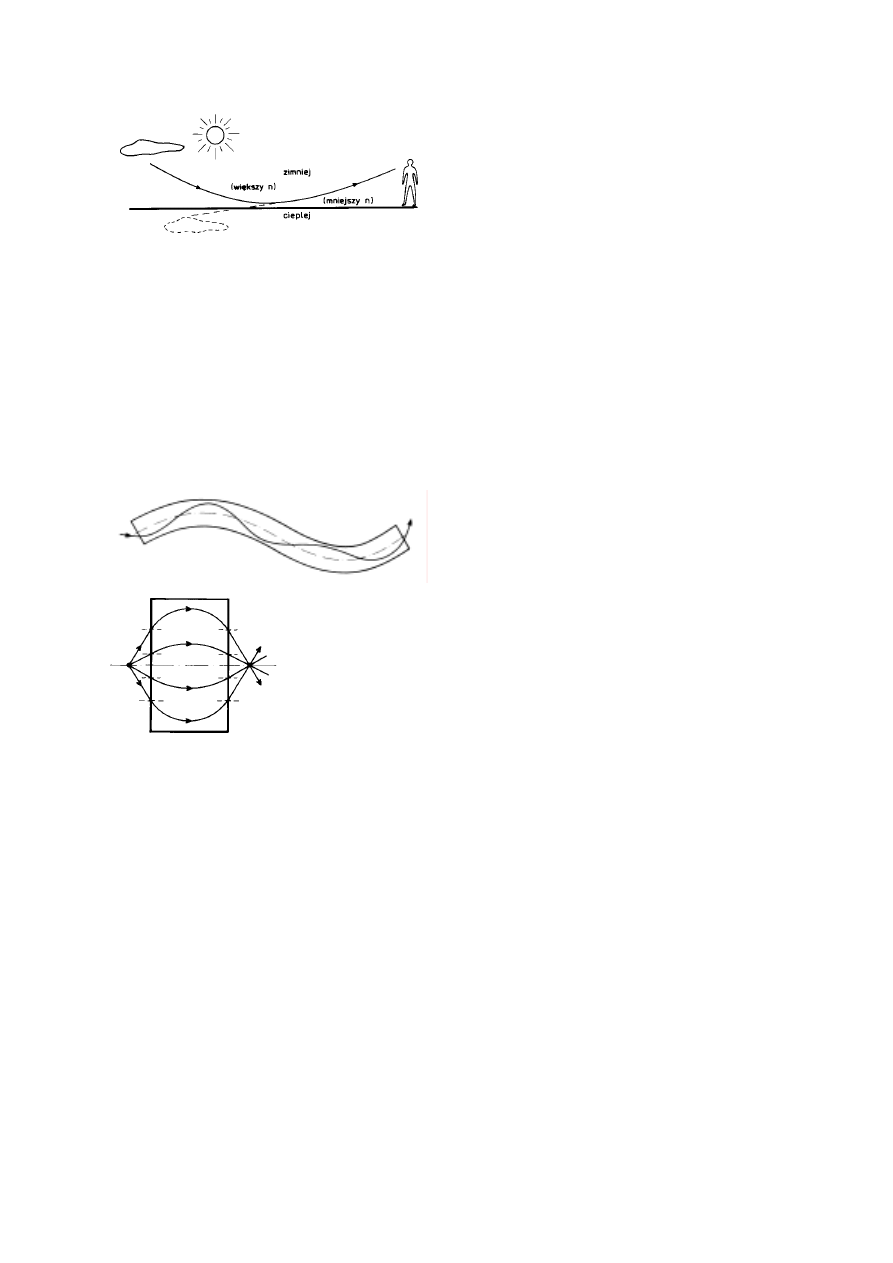
Rys. 12
Rozchodzenie się światła w ośrodku o zmiennym
współczynniku załamania - miraż
Zjawisko zakrzywiania promieni świetlnych biegnących w niejednorodnych ośrodkach może być
celowo wykorzystywane. Wyobraźmy sobie pręt wykonany ze szkła o współczynniku załamania
zmieniającym się tak, by w środku był większy niż na brzegach. Światło "wpuszczone" do
takiego pręta na jednym końcu będzie wędrowało w nim po linii falistej na długie odległości bez
strat - jest to światłowód, wypierający coraz powszechniej miedziane kable w telekomunikacji
(rysunek 13). Krótki kawałek takiego niejednorodnego optycznie pręta działa jak soczewka
(rysunek 14). Jest to soczewka gradientowa. Może niektórzy z Czytelników pamiętają, że
profesor Ambroży Kleks ze znanej książki dla dzieci Jana Brzechwy był wynalazcą "kiełbasy
monoklowej", której plasterek działał jak taka soczewka gradientowa. Ciekawe, czy wynalazcy
soczewek gradientowych czytali książkę Brzechwy?
Rys. 13
Bieg światła w światłowodzie gradientowym
Rys. 14
Bieg światła w soczewce gradientowej ("GRIN")
Pojęcie promienia świetlnego oraz prawa odbicia i załamania są fundamentami optyki
geometrycznej, wiedzy, która między innymi pozwala opisać mechanizm tworzenia obrazów w
lustrach i soczewkach. Wykorzystamy tę wiedzę, by w kolejnych odcinkach wyjaśnić
szczegółowo działanie soczewek okularowych stosowanych do korekcji wad widzenia.
_____________________________________________________________________________
____________
Literatura:
1. J. R. Myer - Arendt "Wstęp do optyki", Państwowe Wydawnictwo Naukowe, Warszawa
1977,
2. J. Nowak, M. Zając "Optyka - kurs elementarny", Oficyna Wydawnicza Politechniki
Wrocławskiej, Wrocław, 1998,
3. O. Sojecki, "Optyka", Wydawnictwa Szkolne i Pedagogiczne, Warszawa 1997,
4. Sz. Szczeniowski, "Fizyka doświadczalna, cz. IV - optyka", Państwowe Wydawnictwo
Naukowe, Warszawa 1963.
© "OKO" i M. Zając'2001