TEORIA SILNIKÓW PRZEPŁYWOWYCH

TEORIA SILNIKÓW PRZEPŁYWOWYCH

Repetytorium z termodynamiki i

mechaniki płynów

Dr inż. Robert Jakubowski

Gaz doskonały

• Gaz hipotetyczny, którego drobiny nie przyciągają się

wzajemnie, są nieskończenie małe i sztywne (nie

występują drgania wewnątrz drobin). Cechuje się on

stałymi wartościami wielkości opisujących jego

właściwości

p

v

c

k

c

=

, ,

p

v

c c k idem

=

Równanie Clapeyrona

pv RT

=

p

v

R c

c

=

−

R [J/(kgK)]– indywidualna stała gazowa – zależy od skaładu gazu

Gaz półdoskonały

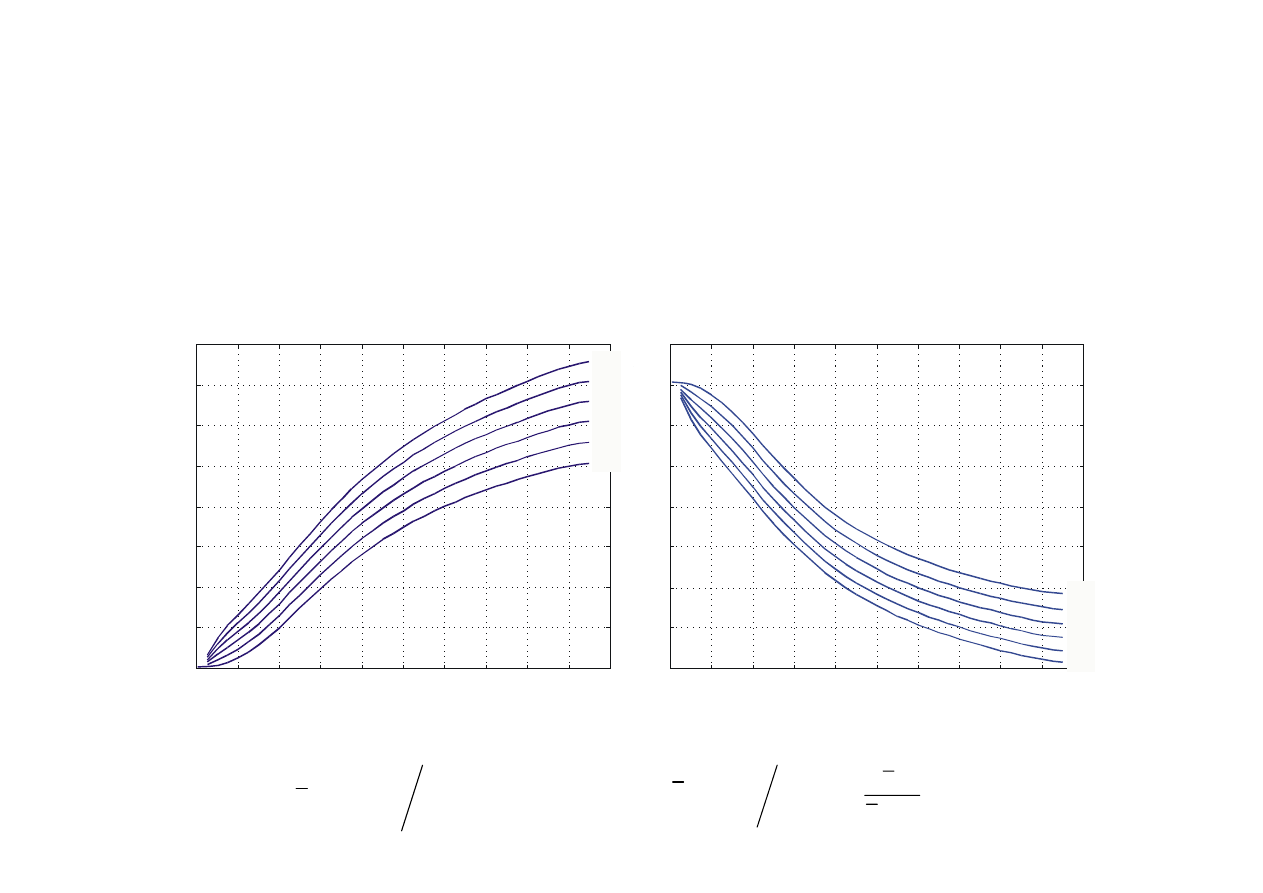
• Gaz w którym uwzględnia się drgania drobin. Wielkości

opisujące właściwości gazu zależą od temperatury

, ,

( )

p

v

c c k

f T

=

200

400

600

800

1000

1200 1400

1600 1800

2200

1000

1050

1100

1150

1200

1250

1300

1400

T [K]

c

P

[J/kgK]

0,05
0,04
0,03
0,02
0,01
0,00

200

400

600

800

1000

1200

1400 1600

1800

2200

1.26

1.28

1.3

1.32

1.34

1.36

1.38

1.4

1.42

k

T [K]

0,00
0,01

0,02
0,03
0,04
0,05

Zależność pojemności cieplnej c

p

oraz wykładnika izentropy k dla spalin powstałych ze spala-nia paliwa o uśrednionym składzie chemicznym

C

12

H

23,5

od temperatury dla różnych wartości względ-nego zużycia paliwa

τ

pal

(dla powietrza

τ

pal

=0)

(

)

2

1

2

1

T

p

p

T

c

k

kdT

T

T

c

R

=

−

=

−

∫

(

)

2

1

2

1

T

p

p

T

c

c dT

T

T

=

−

∫

Gaz rzeczywisty

• W gazach rzeczywistych oprócz temperatury uwzględnia

się wpływ ściśliwości na właściwości gazów

Równanie stanu gazu

pv zRT

=

z – współczynnik ściśliwości gazu

„Niemal wszystkie gazy występujące w technicznych urządzeniach cieplnych

można traktować jako gaz doskonały i półdoskonały. Wyjątek stanowią gazy

pod wysokim ciśnieniem i pary. Na właściwości tych czynników wyraźnie

wpływa objętość właściwa drobin i ich wzajemne przyciąganie. Dlatego

czynniki te należy traktować jak gaz rzeczywisty.”

J. Szargut TERMODYNAMIKA

Równanie ciągłości

dm

m

Ac

dt

ρ

=

=

- wydatek masowy

[

/ ]

m kg s

W przepływie ustalonym wydatek masowy przepływu w każdym przekroju

jest stały:

1

2

3

...

m

m

m

=

=

=

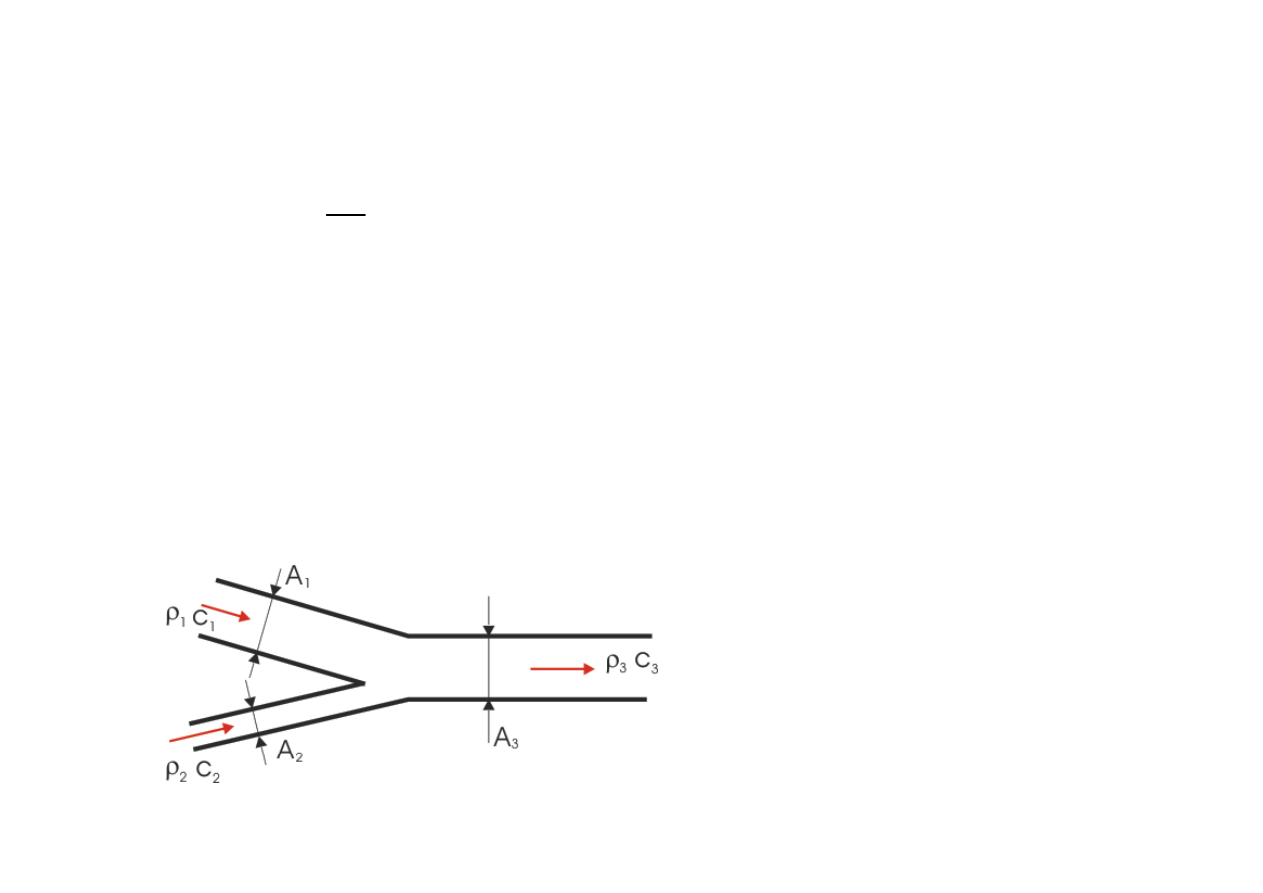
Równanie bilansu masy

1 1 1

2

2 2

3 3 3

A c

A c

A c

ρ

ρ

ρ

+

=

1

2

3

m

m

m

+

=

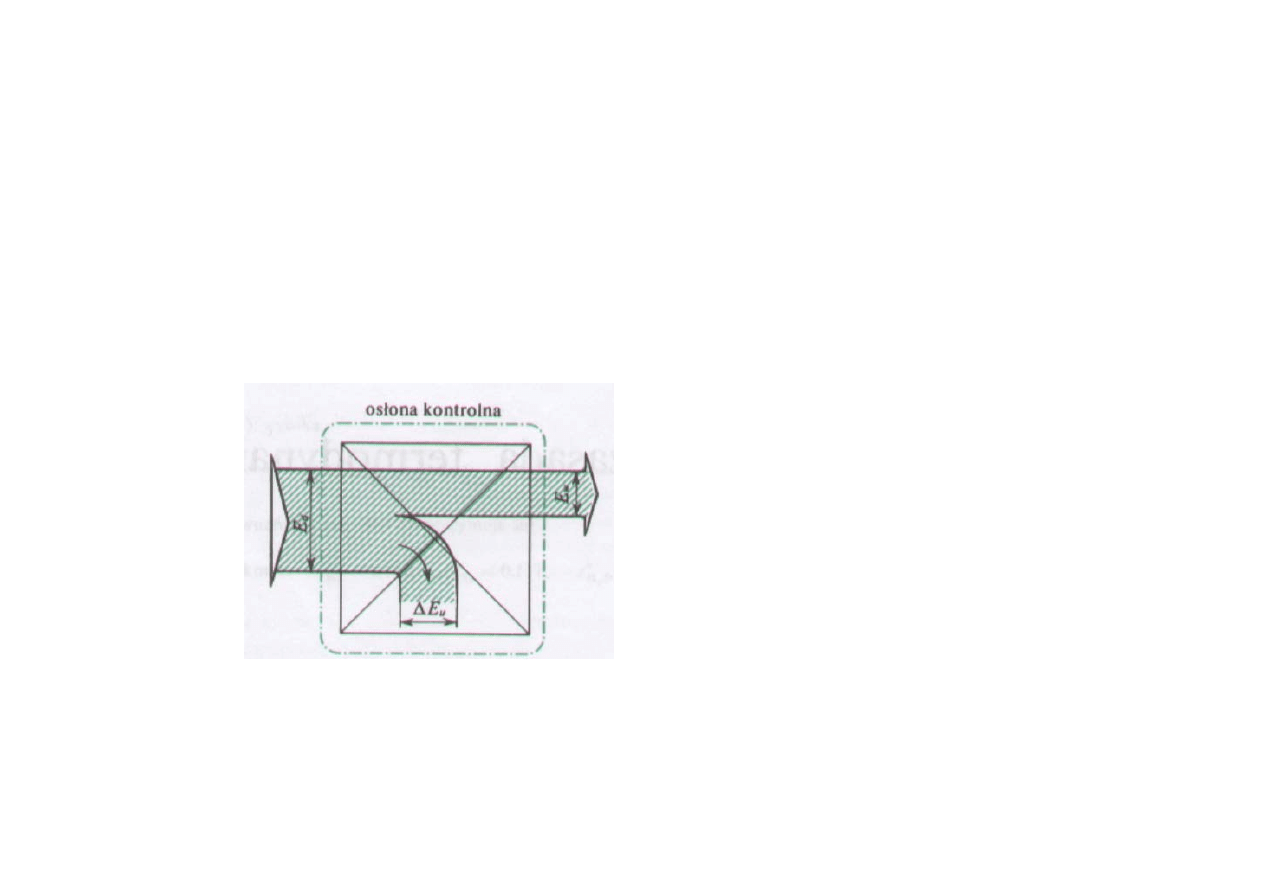
Równanie bilansu energii

(dla wyodrębnionego układu)

D

O

U

E

E

E

=

+ ∆

U

K

P

E

E

E

U

=

+

+

- energia właściwa

/

e E m

=

I Zasada Termodynamiki

dop

Q

L

U

= + ∆

Wykres Sankey’a

Układy otwarte

Funkcja Gibbsa (entalpia)

I U

pV

i u pv

= +

= +

Przedstawione ujęcie entalpii jest

możliwe dla małych prędkości

przepływu

(c<40 m/s)

, inaczej:

2

2

2

(

1 2

)

1 2

1 2

r

C

C

E

m gh

c

i

stąd

I

I

mc

mgh

i

i

c

gh

=

+

+

= +

+

= +

+

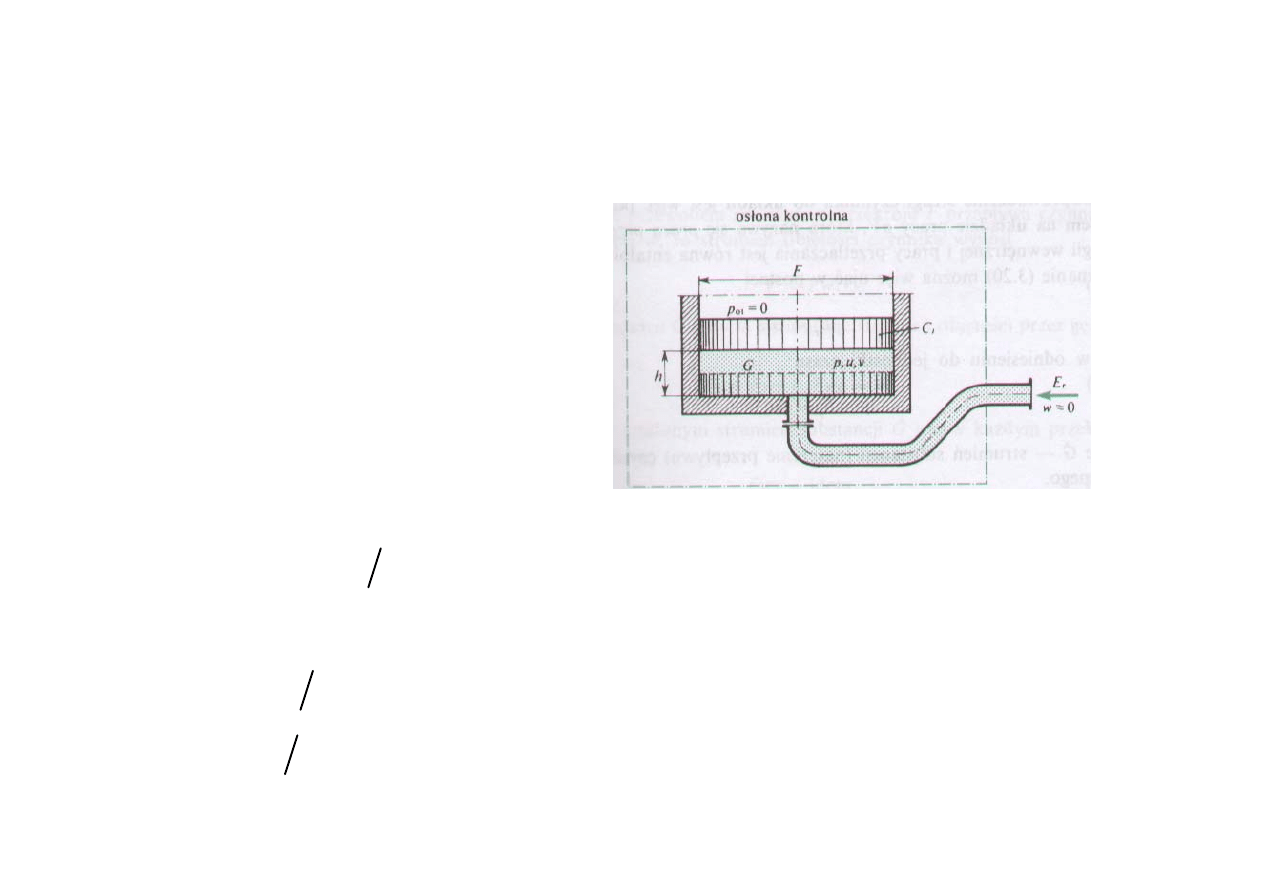
Model do wyjaśnienia energii strugi czynnika

r

t

t

E

U C h

gdzie

C h

pFh

pV

= +

=

=

Praca, praca techniczna

L

t

L

p

p

p

v

v

v

1

1

1

2

2

2

2

1 2

1

dL

pdV

L

pdV

−

=

=

∫

0

0,

0

0,

dV

dL

dV

dL

> ⇒

>

< ⇒

<

2

1 2

1

t

t

dL

Vdp

L

Vdp

−

= −

= −

∫

0

0,

0

0,

t

dp

dL

dp

dL

> ⇒

<

< ⇒

>

dop

dop

t

Q

U L

U

pdV

Q

I L

I

Vdp

= ∆ + = ∆ +

= ∆ +

= ∆ −

∫

∫

I Zasada Termodynamiki

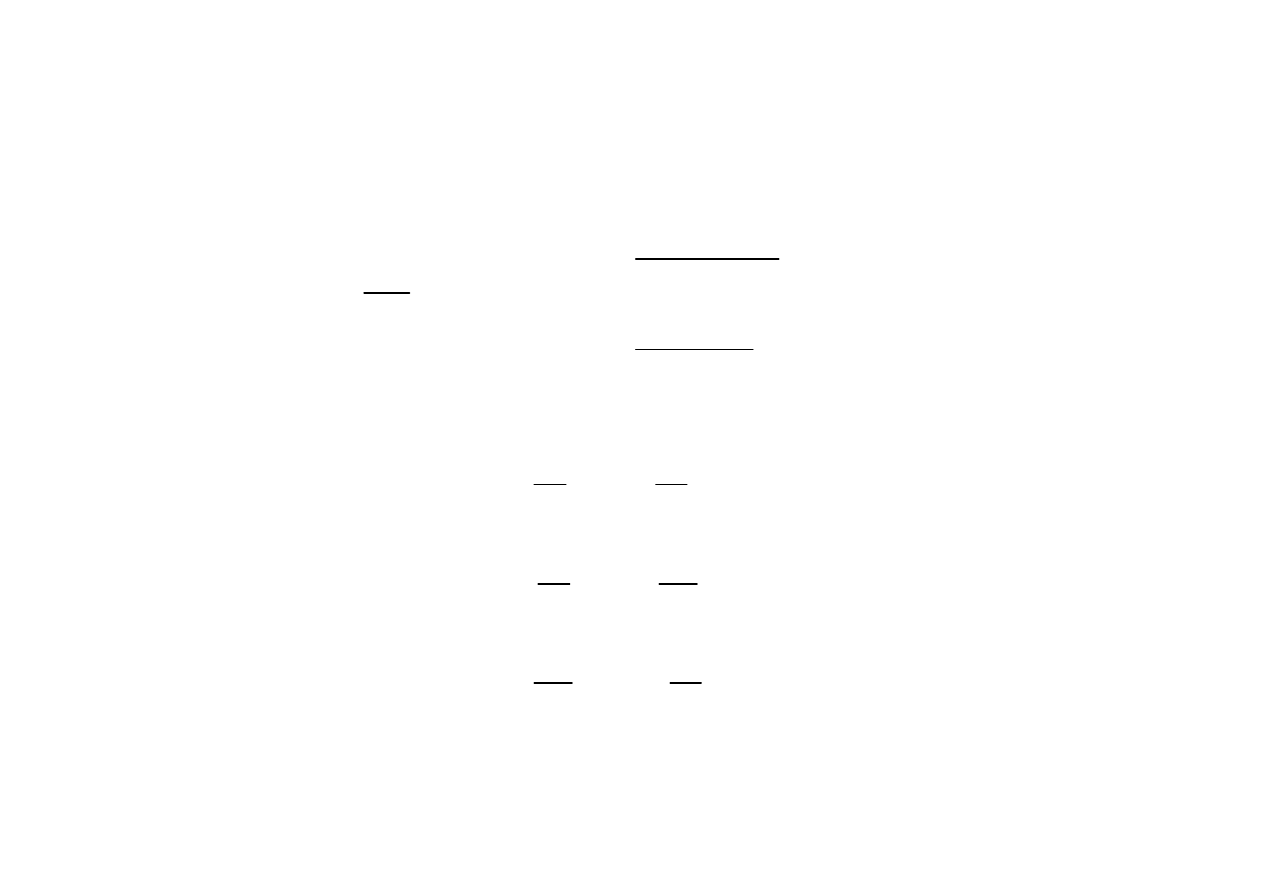
Entropia

Funkcja wprowadzona przez Clausiusa

dU

pdV

dS

T

dI Vdp

dS

T

+

=

−

=

dQ

dS

T

=

⇒

2

2

2

1

1

1

2

2

2

1

1

1

2

2

2

1

1

1

ln

ln

ln

ln

ln

ln

v

p

v

p

T

v

s

s

c

R

T

v

T

p

s

s

c

R

T

p

p

v

s

s

c

c

p

v

− =

+

− =

−

− =

+

Charakterystyczne przemiany gazów

PRZEMIANA IZOTERMICZNA T=idem

pv RT

pv idem

=

⇒

=

1 1

2 2

p v

p v

=

1

2

2

1

p p

v v

=

p

v

T

T

T

T

T

T

1

1

2

2

3

3

>

>

T

s

1 2

1 2

2

1

1

1 2

1 1

1 1

1

2

2

ln

ln

ln

t

Q

L

L

V

p

p

L

p V

p V

mRT

V

p

p

−

−

−

=

=

=

=

=

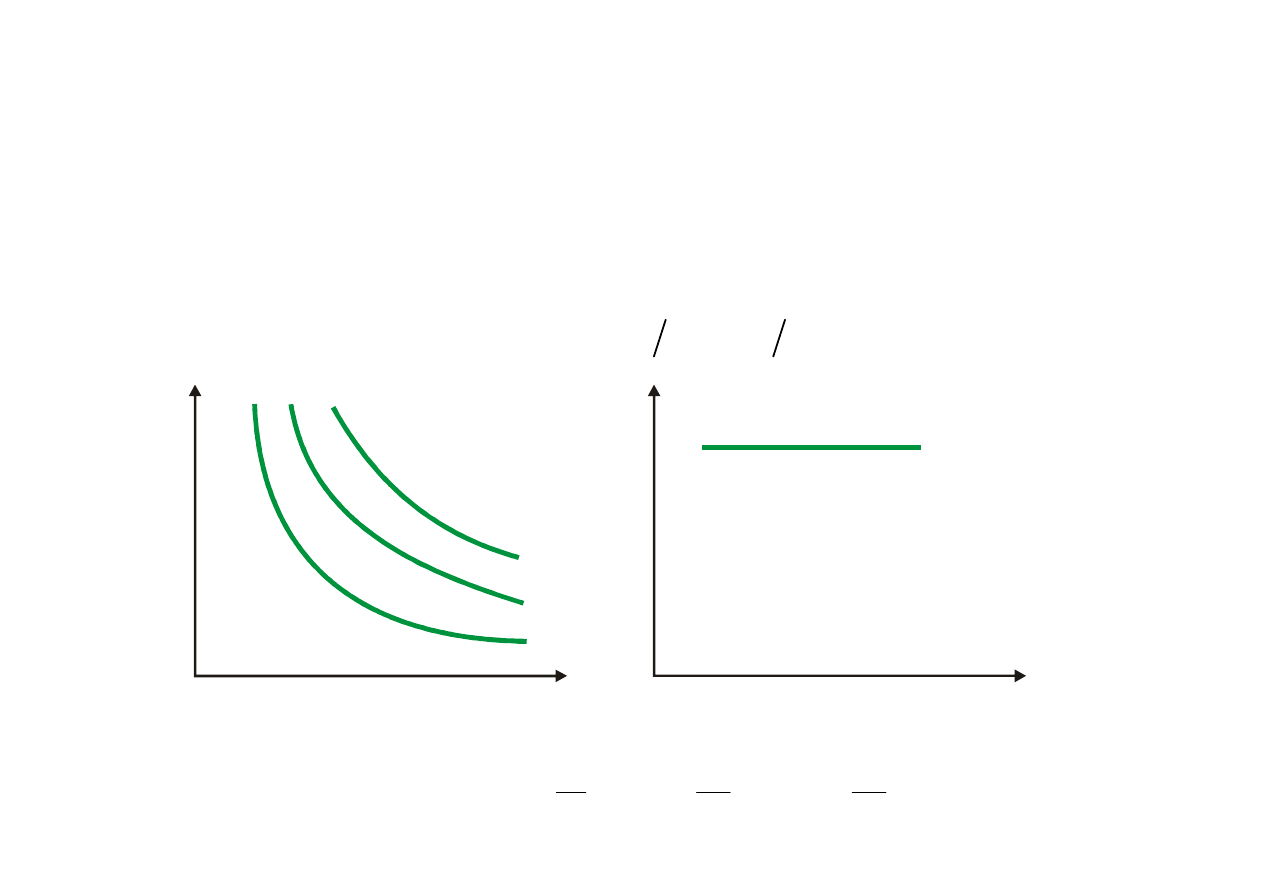
Charakterystyczne przemiany gazów

PRZEMIANA IZOCHORYCZNA V=idem

pv RT

p T idem

=

⇒

=

1

1

2

2

p T

p T

=

1

2

1

2

p p

T T

=

p

v

T

T

1

2

1

2

L

t

1 2

1

2

0

(

)

t

L

L

V p

p

−

=

=

−

Ciepło pobrane przez czynnik

z I ZT przy L=0

(

)

2

1

1 2

2

1

T

v T

Q

U

mc

T

T

−

= ∆ =

−

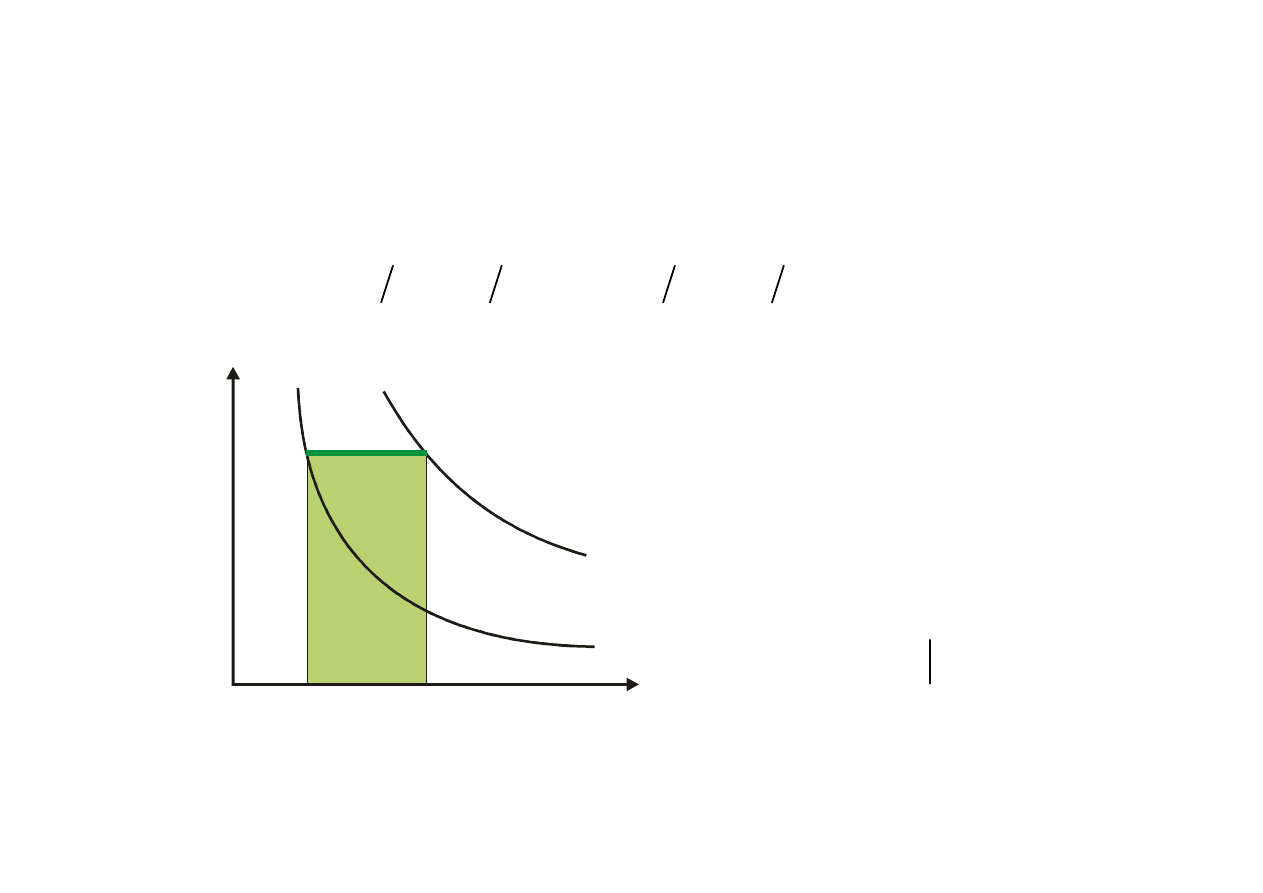
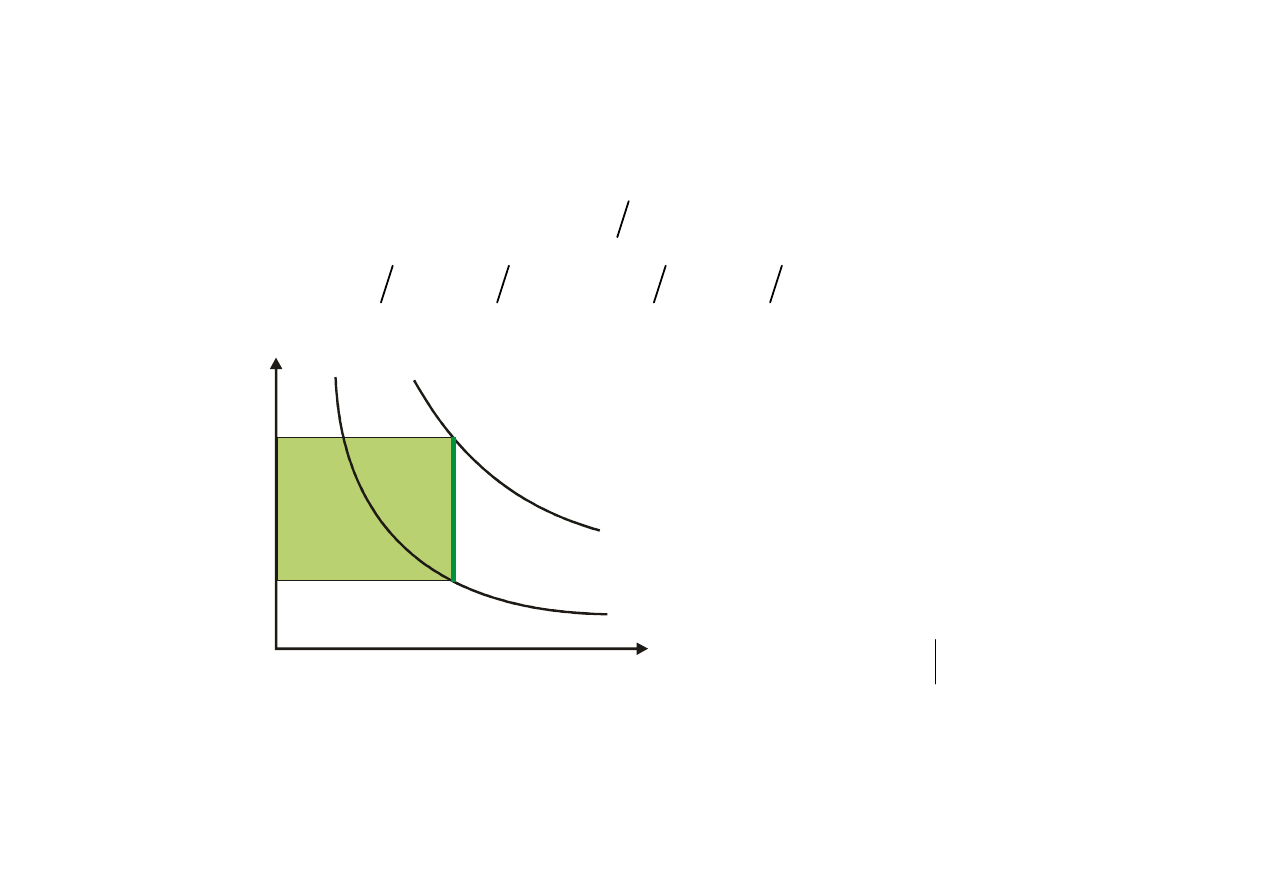
Charakterystyczne przemiany gazów

PRZEMIANA IZOBARYCZNA p=idem

/

pv RT

v T idem

=

⇒

=

1

1

2

2

v T

v T

=

1

2

1

2

v v

T T

=

p

v

T

T

1

2

1

2

L

1-2

1 2

2

1

0

(

)

t

L

L

p V

V

−

=

=

−

Ciepło pobrane przez czynnik

z I ZT przy L

t

=0

(

)

2

1

1 2

2

1

T

p T

Q

I

mc

T

T

−

= ∆ =

−

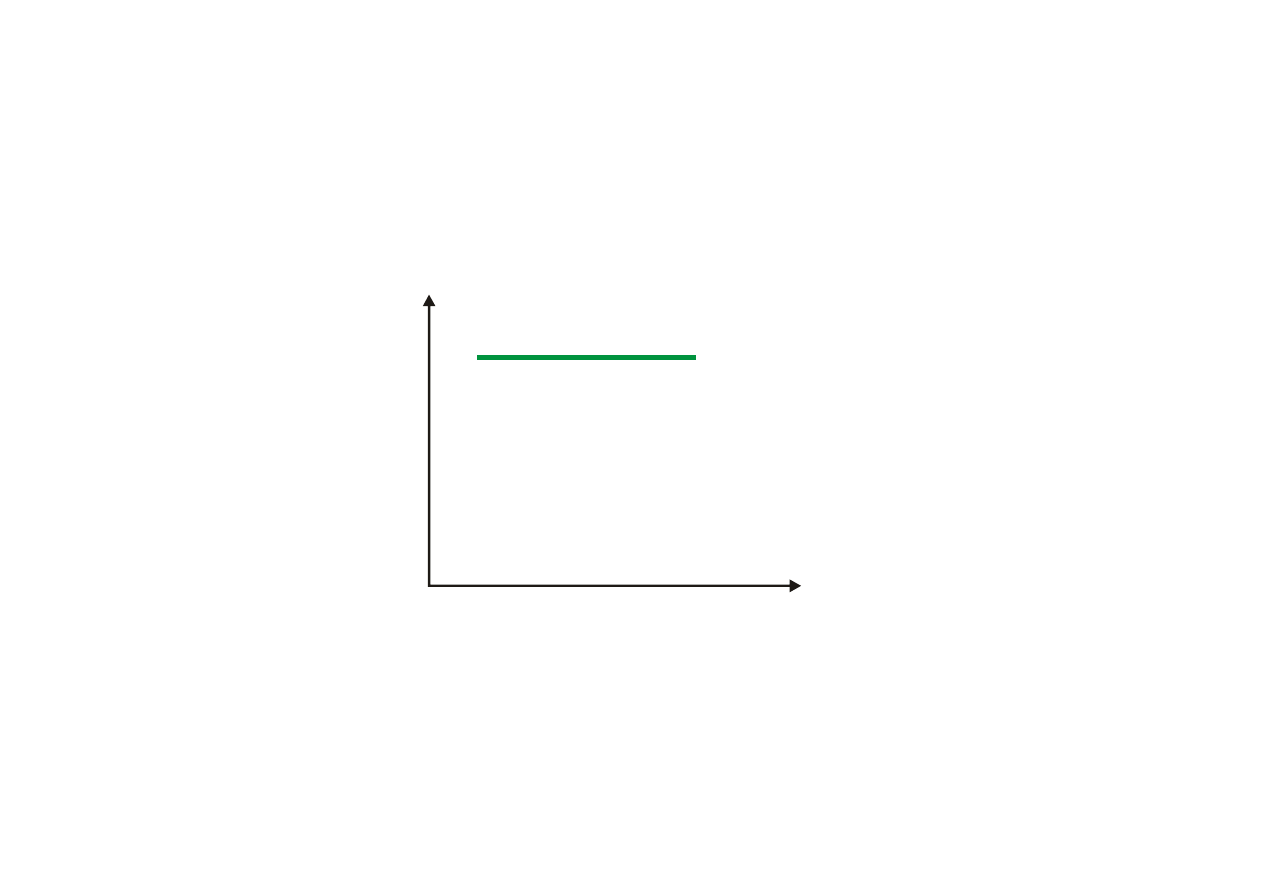
Charakterystyczne przemiany gazów

PRZEMIANA IZENTALPOWA I=idem

(

)

1 2

2

1

t

p

Q

L

c T

T

−

=

=

−

i

s

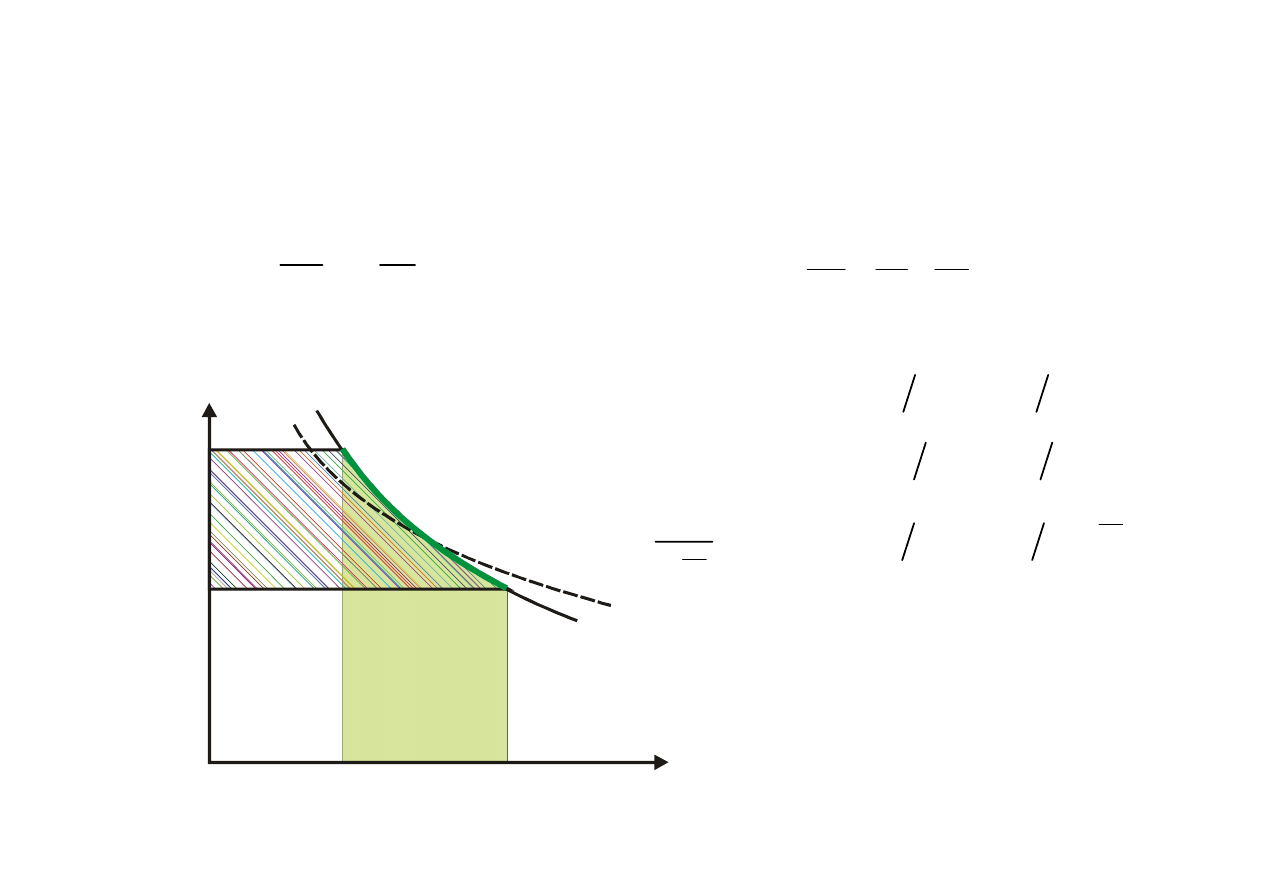
Charakterystyczne przemiany gazów

PRZEMIANA IZENTROPOWA s=idem

Równanie różniczkowe izentropy

Równanie Clapeyrona po zróżniczkowaniu

0

v

dT

dv

c

R

T

v

+

=

( )

ln

ln

ln

k

k

v

p C

v p

idem

+

= ⇒

=

(

)

1 2

1 2

1

2

1

2

1 2

0

(

)

v

t

p

t

Q

L

U

mc T T

L

I

mc T T

L

kL

−

−

−

=

= −∆ ⇒

−

= −∆ =

−

=

dT

dv dp

T

v

p

=

+

p

v

T

T=idem

s=idem

1

1

2

L

L

1-2

t

(

)

(

)

(

)

1

1

1

2

2

1

1

1

1

2

2

1

1

2

1

2

k

k

k

k

k

k

k

k

v p idem

p p

v v

Tv

idem

T T

v v

T

idem

T T

p p

p

−

−

−

−

=

⇔

=

=

⇔

=

=

⇔

=

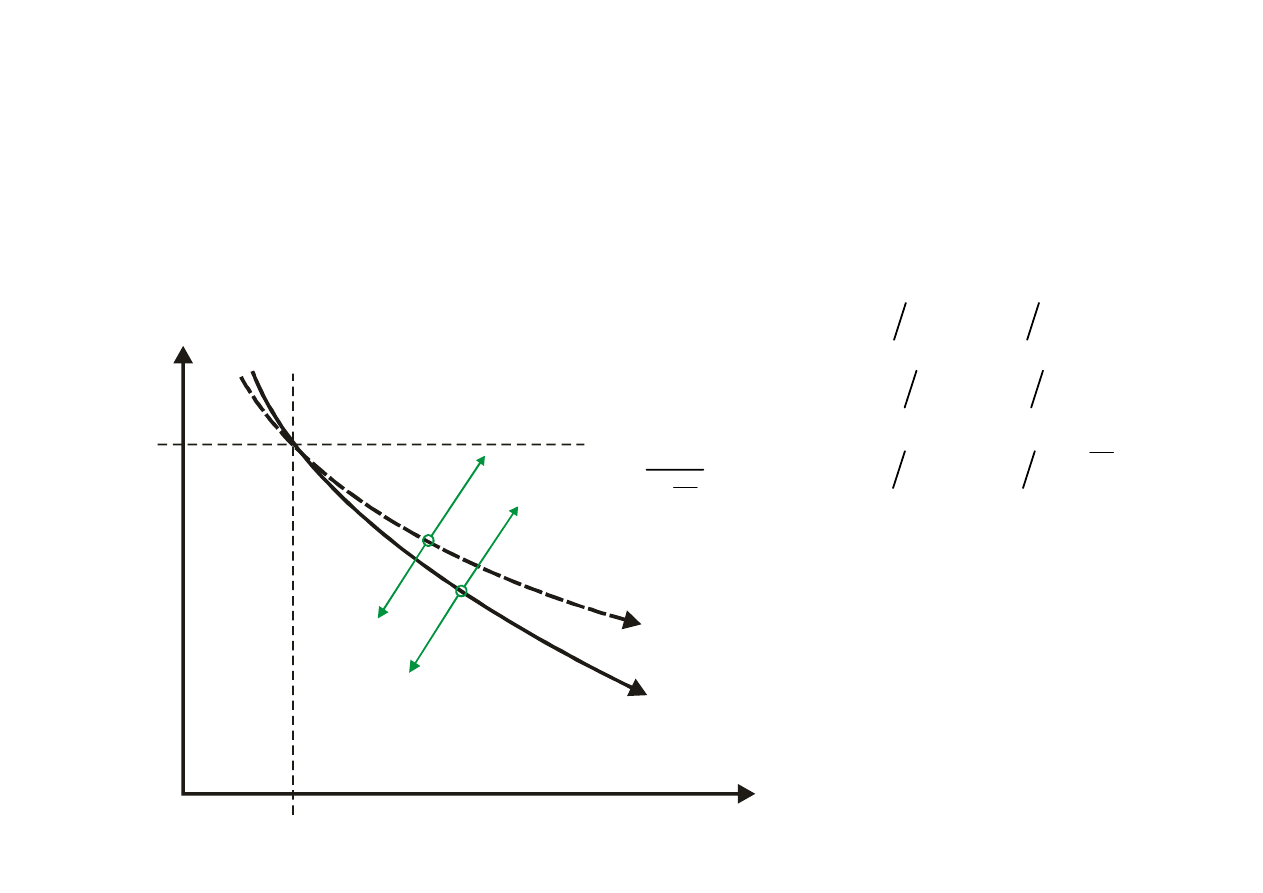
Charakterystyczne przemiany gazów

PRZEMIANA POLITROPOWA

n

pv

idem

=

(

)

(

)

(

)

1

1

1

2

2

1

1

1

1

2

2

1

1

2

1

2

n

n

n

n

n

n

n

n

v p idem

p p

v v

Tv

idem

T T

v v

T

idem

T T

p p

p

−

−

−

−

=

⇔

=

=

⇔

=

=

⇔

=

p

v

T

T=idem

s=idem

1

d

v=

0,

n=ni

e

sk

, c

=

c

v

dp=0, n=0, c=c

p

dQ=

0, n=

k

dT=0, n

=1

dQ

>0

dQ

<0

dT

<0

dT

>0

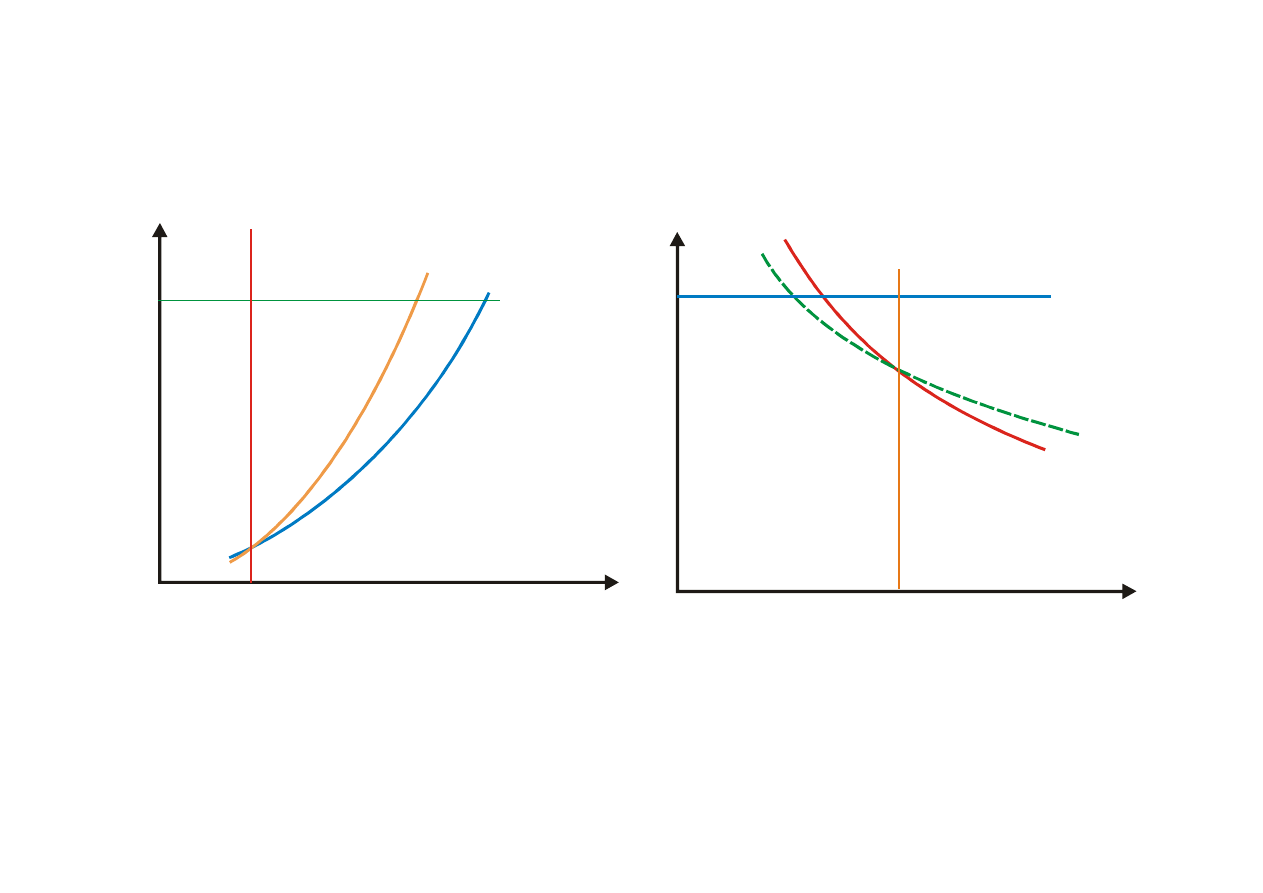
Zobrazowanie przemian na wykresie i-s

i

s

ds

=0

,

di =0

dp

=

0

dv

=

0

p

v

dT=0

ds=0

dp=0

dv

=

0

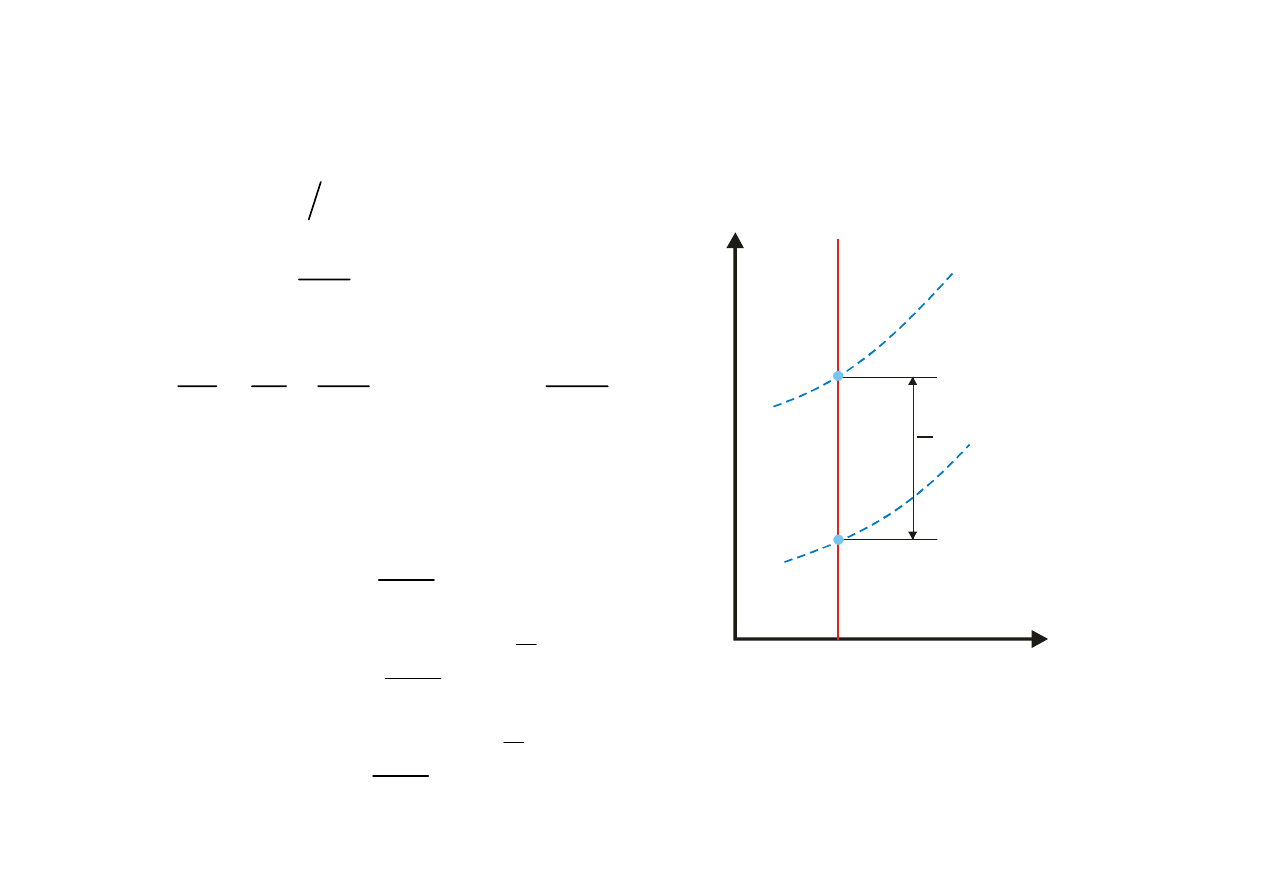
Równanie przepływu izentropowego

i

s

ds

=0

1

1*

*

c

2

2

1

1

1

p

p

*

2

1

1

2

*

1

1

*

2

2

*

1

1

1

1

1

*

1

1

2

2

2

2

p

p

p

i

i

c

c

T

T

c

p

p

c

c

p

p

c

c

ρ

ρ

ρ

= +

= +

=

+

⇒

=

+

Dla przepływów ściśliwych

1

1

1

*

2

1

1

*

2

1

1

*

2

1

1

1

1

2

1

1

2

1

1

2

k

k

k

k

T

T

Ma

k

p

p

Ma

k

v

v

Ma

−

−

−





=

+









−





=

+









−





=

+









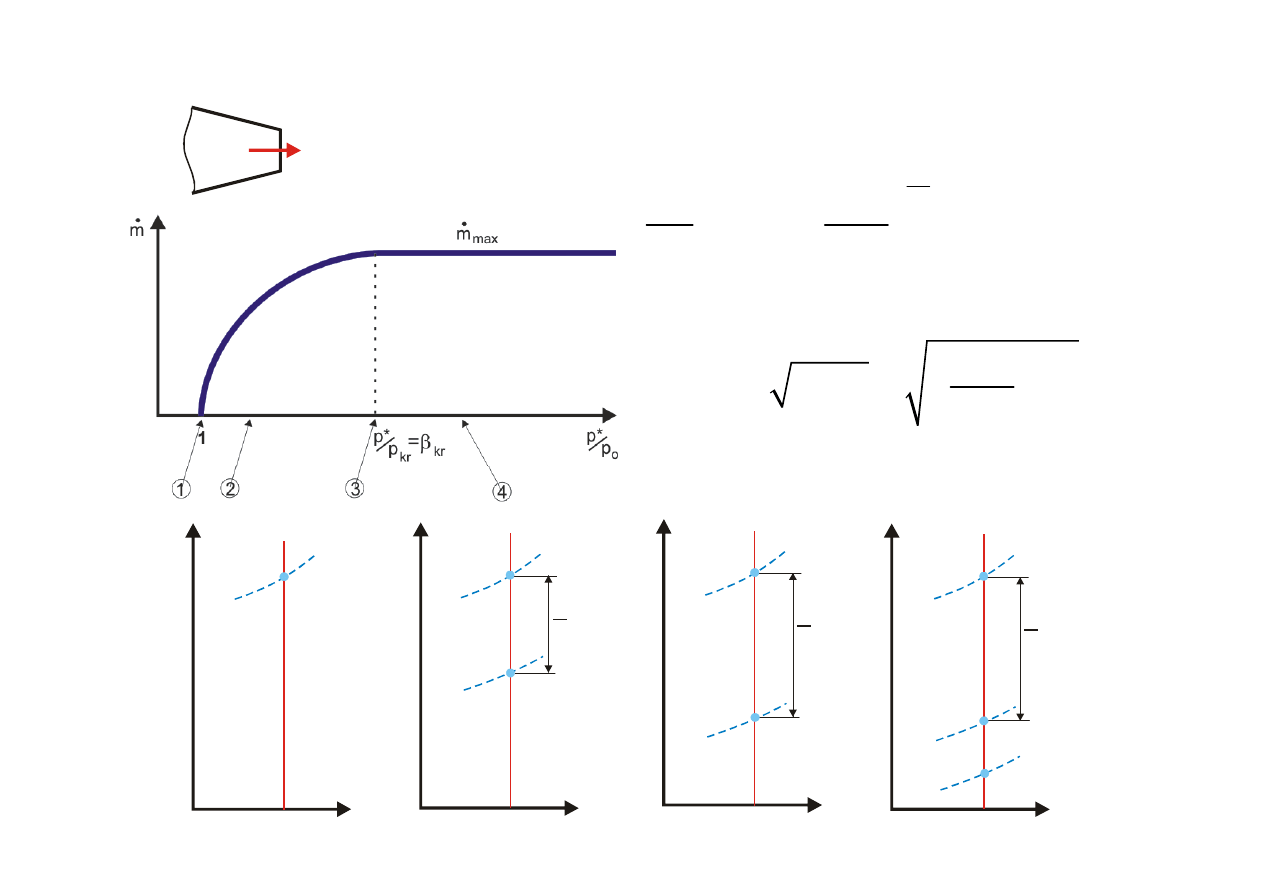
Maksymalny wydatek przepływu

p*

p

c

o

1

*

*

1

2

1, 4

1,893

2

1

k

k

kr

kr

kr

kr

kr

kr

kr

kr

p

k

p

k

k

c

a

kRT

RT

k

m

Ac

β

β

ρ

−

+





=

= 







=

⇒

≈

= =

=

+

=

i

s

*

c

2

2
kr

kr

0

p

p

=p

i

s

*

c

2

2

0

p

p

i

s

*

0

p =p

s

*

c

2

2
kr

kr

0

p

p

p

i

4)

1)

2)

3)

Równania dla przepływu krytycznego

1

Ma

=

1

1

1

2

*

*

*

*

*

,

:

2

2

1

2

1

2

1

2

k

k

k

a

i

i

gdzie a

kRT

i

i

k

T

T

k

p

p

k

v

v

−

−

= +

−

= +

+

=

+





= 







+





= 







Parametry statyczne

przepływającego czynnika

noszą nazwę parametrów

krytycznych

kr

p

p

⇔

prędkość dźwięku

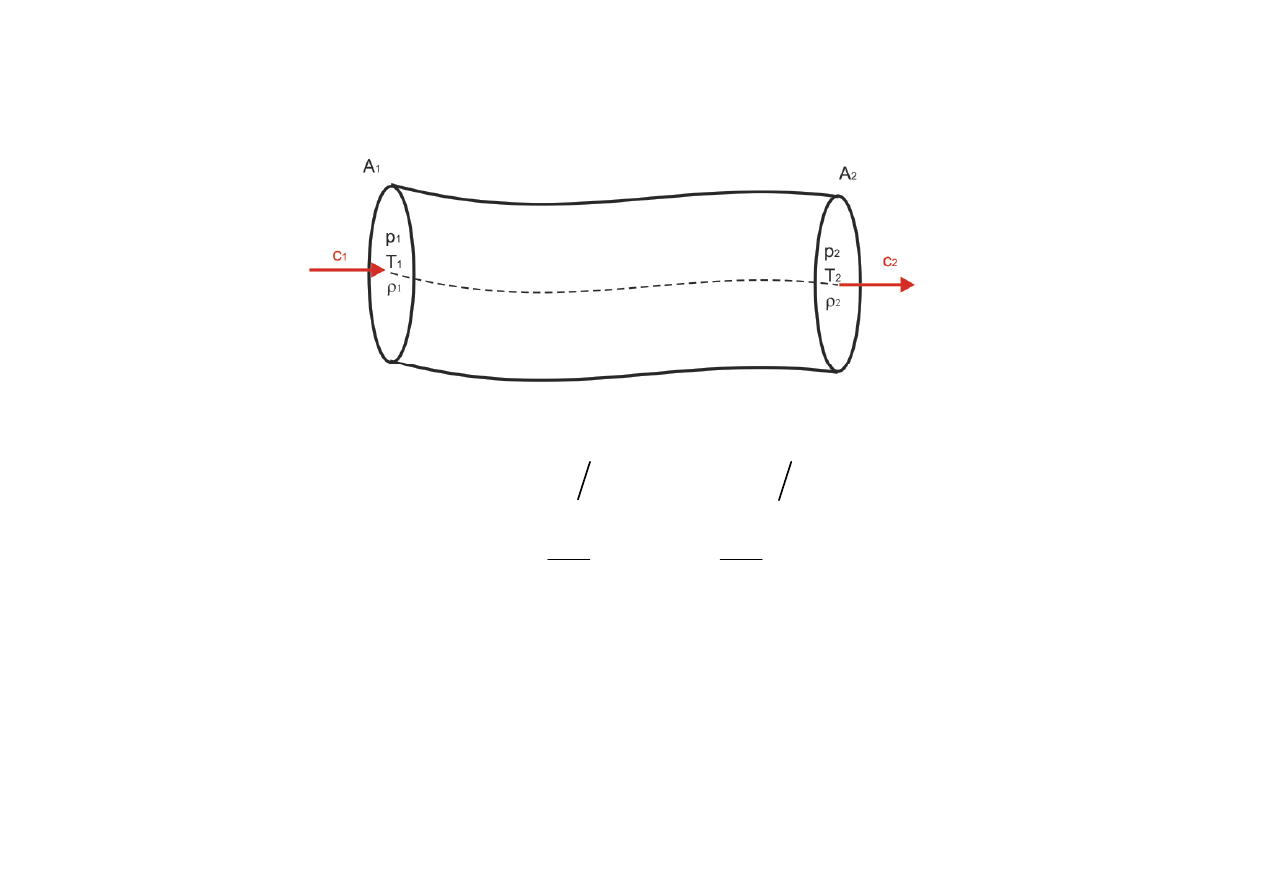
Przepływ ustalony przez kanał bez wymiany ciepła

Z I zasady termodynamiki:

*

2

2

*

2

1

1

2

2

2

2

2

i

i

c

i

i

c

= +

= = +

*

*

*

1

2

i

idem

i

i

=

⇔ =

2

2

*

*

1

2

1

1

2

2

2

2

p

p

c

c

T

T

T

T

c

c

= +

=

=

+

Przepływ ze stratami:

*

*

1

2

p

p

>

σ

gdzie

- współczynnik strat ciśnienia

*

*

2

1

p

p

σ

=

Z równania ciągłości:

1

2

m

m

=

1 1 1

2

2 2

A c

A c

ρ

ρ

=

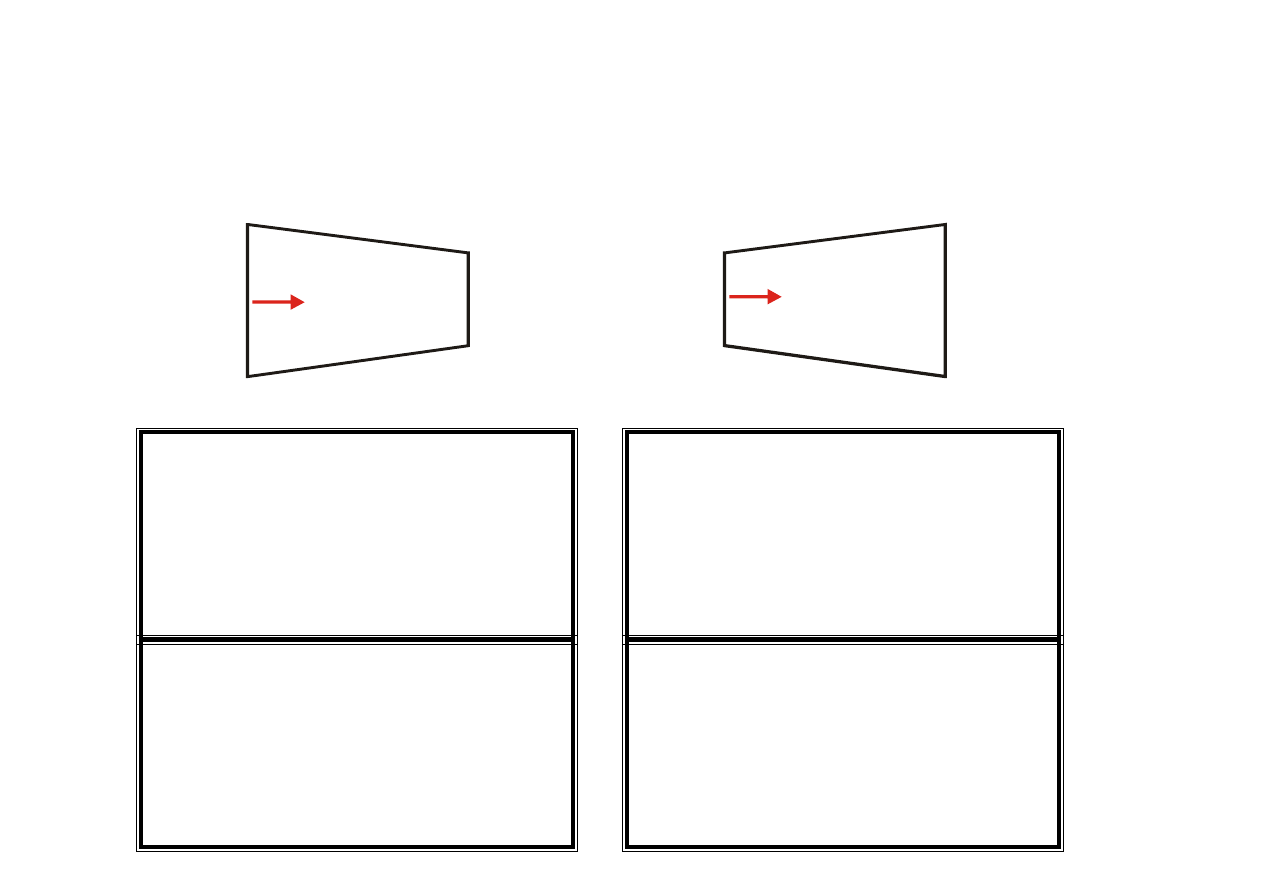
Przepływ przez kanał o zmiennym polu przekroju

KANAŁ ZBIEŻNY

KANAŁ ROZBIEŻNY

dA>0

c

dA<0

c

Gdy c<a, Ma<1

dc>0, dp<0, d

ρ<0, dT<0

D Y S Z A

Gdy c<a, Ma<1

dc<0, dp>0, d

ρ>0, dT>0

D Y F U Z O R

Gdy c>a, Ma>1

dc<0, dp>0, d

ρ>0, dT>0

D Y F U Z O R

dc>0, dp<0, d

ρ<0, dT<0

D Y S Z A

Gdy c>a, Ma>1

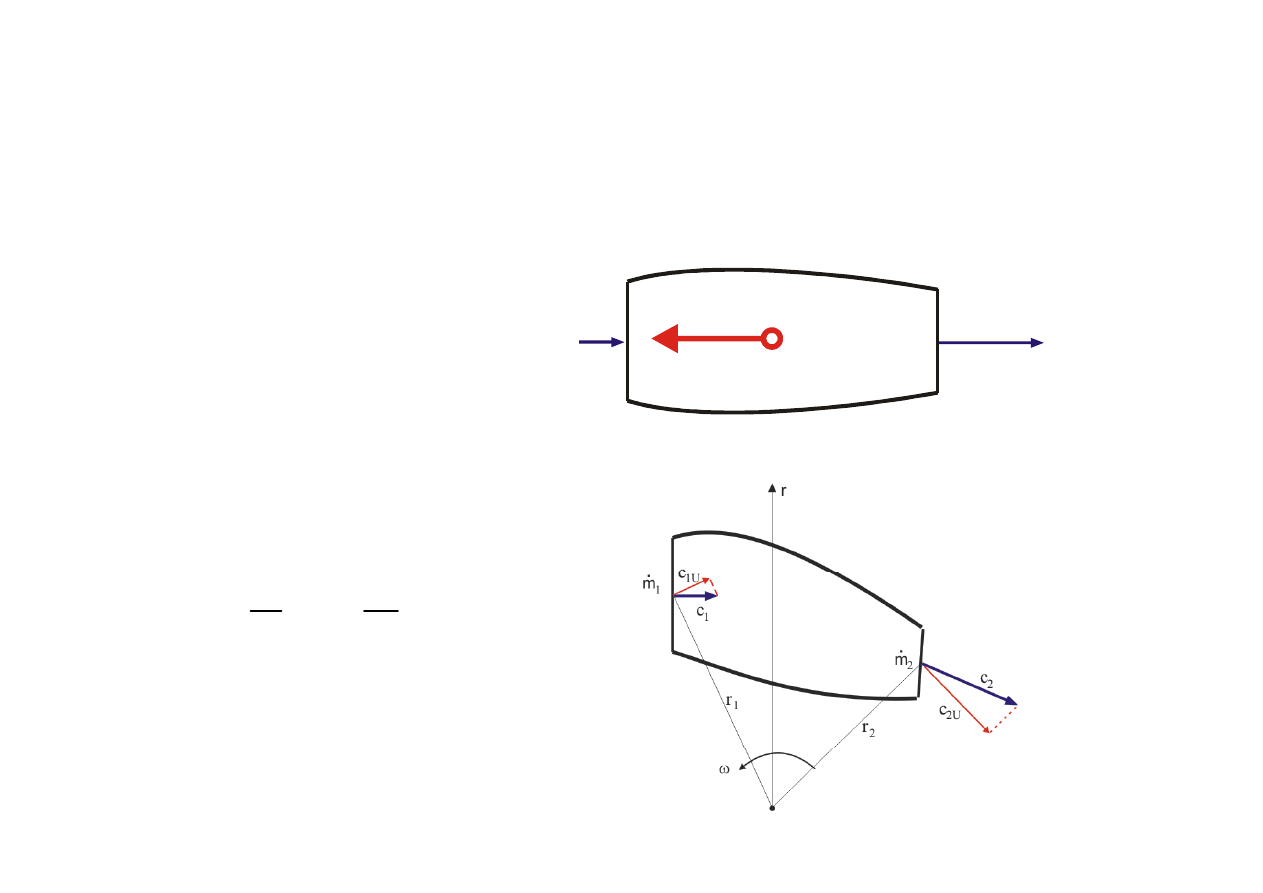
Równanie pędu i momentu pędu (równania Eulera)

Równanie pędu

c

c

1

2

1

2

m

m

.

.

F

2

2

1 1

F m C

m C

=

−

Równanie momentu pędu

2

2U 2

1 1U 1

M m C r

m C r

=

−

u

l

P

M

m

= =

ω

ω

gdzie PRACA UNOSZENIA

u

2

2U

1 1U

l

u C

u C

=

−

u

r

= ω

- prędkość unoszenia