Z. Kąkol-Notatki do Wykładu z Fizyki

16-1

Wykład 16

16. Kinetyczna teoria gazów i termodynamika I

16.1 Prawo gazów doskonałych

Gaz doskonały:

•

objętość cząsteczek gazu jest o wiele mniejsza niż objętość zajmowana przez gaz,

•

zasięg sił działających między dwoma cząstkami jest o wiele mniejszy niż średnia

odległość międzycząsteczkowa.
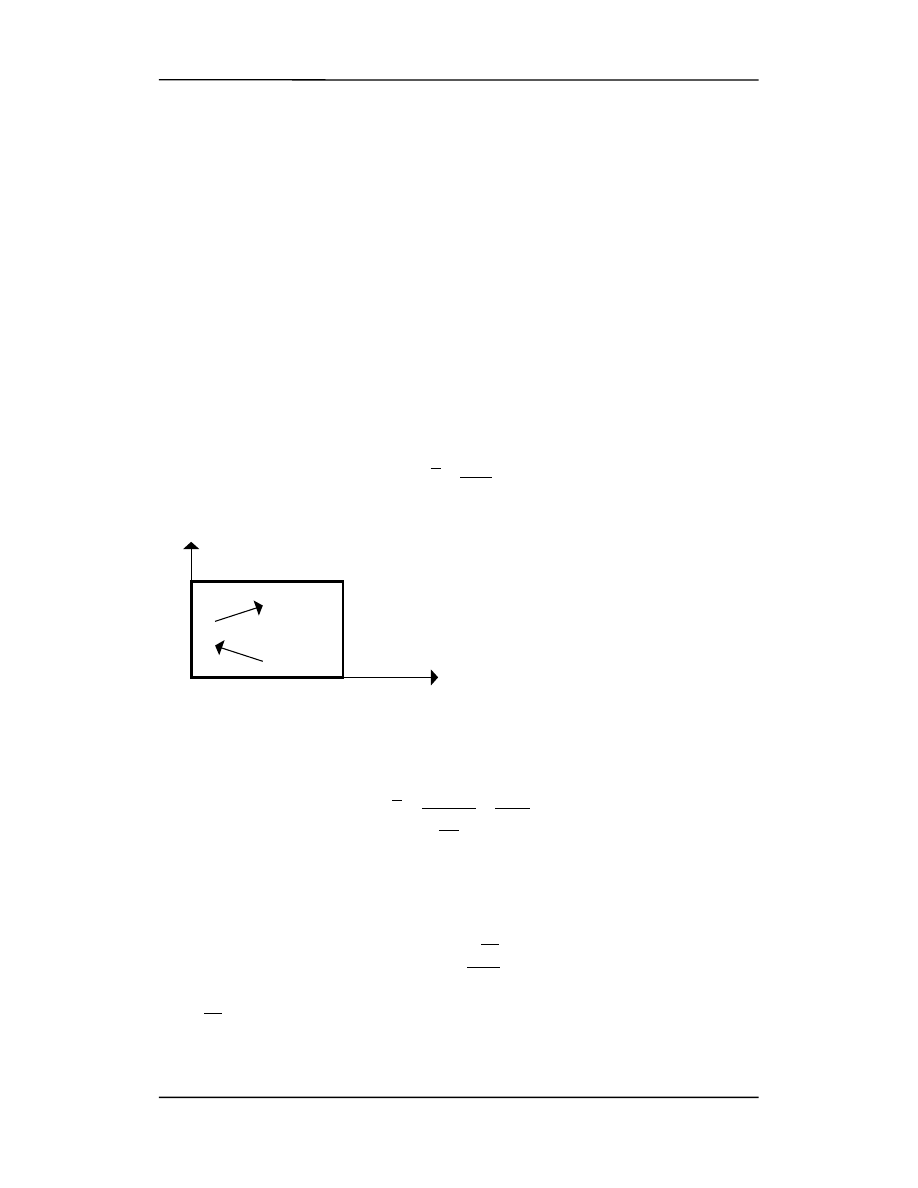
W wyprowadzeniu prawa gazów doskonałych będziemy traktować cząsteczki gazu jako
N małych, twardych kulek zamkniętych w pudełku o objętości V. Kulki są twarde tzn.
będą zderzały się sprężyście ze ściankami naczynia. Rozważmy jedną cząsteczkę, która
zderza się z lewą ścianką naczynia (rysunek). Średnia siła jaką cząsteczka wywiera na
ściankę w czasie

∆

t wynosi

t

p

F

x

d

d

=

Zmiana pędu spowodowana zderzeniem ze
ścianką wynosi

∆

p

x

= mv

x

- ( - mv

x

) = 2mv

x

Ponieważ czas pomiędzy kolejnymi zderze-
niami z tą ścianką wynosi

∆

t = 2l/v

x

gdzie l jest odległością między ściankami, to

l

m

l

m

F

x

x

x

2

2

)

2

(

v

v

v

=

=

jest średnią siłą działającą na ściankę (na jedną cząstkę).
Dla N cząstek całkowita siła wynosi

l

m

N

F

x

2

v

=

gdzie

2
x

v

jest to

2
x

v

uśrednione po wszystkich cząsteczkach (średnia kwadratu). Dzieląc

obie strony równania przez pole powierzchni ścianki S otrzymujemy ciśnienie

x

y

-v

x

v

x

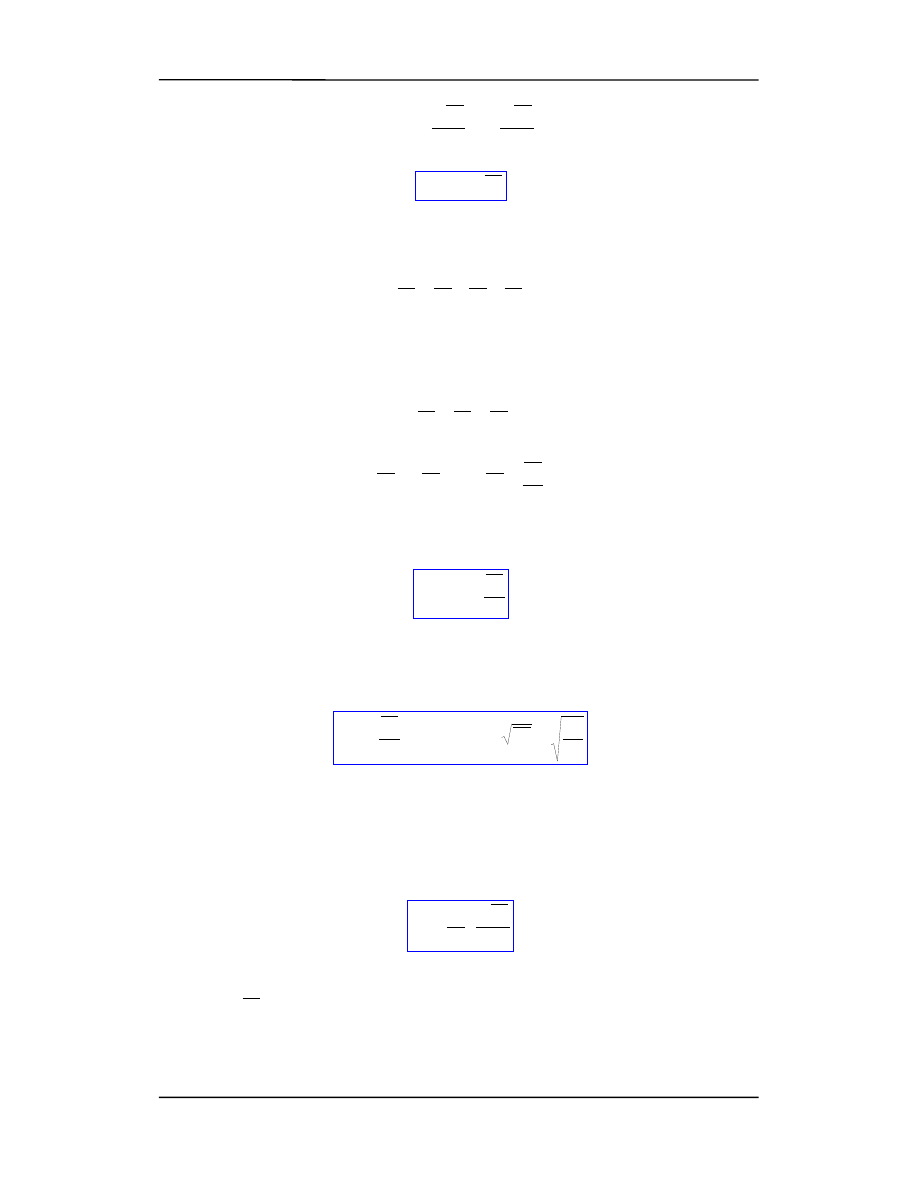
Z. Kąkol-Notatki do Wykładu z Fizyki

16-2

V

m

N

Sl

m

N

P

x

x

2

2

v

v

=

=

czyli

2
x

Nm

pV

v

=

(16.1)

Jak widać iloczyn pV jest stały tak długo jak długo jest stała energia kinetyczna cząstek
(prawo Boyle'a - Mariotta).
Zauważmy, że

2

2

2

2

z

y

x

v

v

v

v

+

+

=

Ponadto, ponieważ cząstki zderzają się w taki sam sposób ze wszystkimi sześcioma
ściankami naczynia więc

2

2

2

z

y

x

v

v

v

=

=

więc

3

,

3

2

2

2

2

v

v

v

v

=

=

x

x

czyli

Teraz otrzymujemy równanie wyrażone przez v a nie przez v

x

3

2

v

Nm

pV

=

(16.2)

Ponieważ Nm = M (masa gazu), oraz M/V =

ρ więc równanie powyższe można przepi-

sać w postaci

ρ

ρ

p

p

kw

sr

3

,

3

2

.

.

2

=

=

=

v

v

v

czyli

(16.3)

16.2 Temperatura

Zdefiniujmy temperaturę bezwzględną jako wielkość wprost proporcjonalną do

średniej energii kinetycznej cząstek

2

3

2

2

v

m

k

T













=

(16.4)

gdzie k jest stałą Boltzmana k = 1.38·10

-23

J/K.

Eliminując

2

v

z równań (16.2) i (16.4) otrzymujemy

pV = NkT

Z. Kąkol-Notatki do Wykładu z Fizyki

16-3

lub

pV = nRT

(16.5)

gdzie n jest liczbą moli (R = kN

AV

). Przypomnijmy, że stała Avogadra N

Av

= 6.023·10

23

1/mol, określa liczbę cząsteczek w jednym molu.
Wyrażenie (16.5) przedstawia

równanie stanu gazu doskonałego

.

Równanie stanu gazu doskonałego zostało sformułowane w XIX w. przez Clapeyro-

na na podstawie trzech praw empirycznych odkrytych wcześniej przez innych badaczy:

•

Prawo Boyle'a-Mariotte'a stwierdza, że w stałej temperaturze iloczyn ciśnienia i ob-
jętości danej masy gazu jest stały pV = const.

•

Prawo Charlesa mówi, że przy stałej objętości gazu stosunek ciśnienia i temperatury
danej masy gazu jest stały p/T = const.

•

Prawo Gay-Lussaca stwierdza, że dla stałego ciśnienia stosunek objętości do tempe-
ratury danej masy gazu jest stały V/T = const.

16.2.1 Termometry

Aby zmierzyć temperaturę trzeba wyznaczyć energię kinetyczną cząsteczek gazu co jest
bardzo trudne. Ale możemy się posłużyć równaniem stanu gazu doskonałego. Łatwo
jest zmierzyć iloczyn pV np. dla układu o stałym ciśnieniu.

16.3 Ekwipartycja energii

16.3.1 Zerowa zasada termodynamiki

Jeżeli dwa ciała o różnych temperaturach zetkniemy ze sobą (i odizolujemy od in-

nych) to po dostatecznie długim czasie ich temperatury wyrównają się. Powiemy, że te
ciała są w

równowadze termicznej

ze sobą.

Jeżeli ciała 1 i 2 są w równowadze termicznej i ciała 2 i 3 są w równowadze termicznej
to ciała 1 i 3 są w tej samej równowadze termicznej

.

To jest zerowa zasada termodynamiki. Z zasad dynamiki Newtona można pokazać, że
średnie energie kinetyczne ruchu postępowego (na cząsteczkę) dla dwu kontaktujących
się gazów są równe.

16.3.2 Ekwipartycja energii

Wiemy już, że w równowadze termodynamicznej energie kinetyczne ruchu postę-

powego wszystkich cząsteczek są równe. Ale co z ruchem obrotowym i drganiami? Czy
cząsteczka może gromadzić energię w innej postaci niż energia ruchu postępowego?
Jeżeli tylko cząstka nie ma kształtu kuli (1 atomowa) a ma pewną strukturę wewnętrzną
to może wirować i drgać. Np. dwuatomowa w kształcie hantli zacznie się obracać po
zderzeniu. Na podstawie mechaniki statystycznej można pokazać, że

gdy liczba punk-

tów materialnych jest bardzo duża i obowiązuje mechanika Newtonowska to dostępna
energia rozkłada się w równych porcjach na wszystkie niezależne sposoby, w jakie czą-
steczka może ją absorbować

. Każdy z tych sposobów absorpcji energii nazywa się

stop-

niem swobody

i jest równy liczbie niezależnych współrzędnych potrzebnych do określe-

nie położenia ciała w przestrzeni.

Z. Kąkol-Notatki do Wykładu z Fizyki

16-4

Innymi słowy:

średnia energia kinetyczna na każdy stopień swobody jest taka sama dla

wszystkich cząsteczek

. Ten wynik nazywamy zasadą

ekwipartycji energii

.

Średnia energia kinetyczna ruchu postępowego (z równania definiującego T) wynosi

kT

m

2

3

2

1

2

=

v

Odpowiada to trzem stopniom swobody (współrzędne x, y, z). Stąd

średnia energia na

stopień swobody wynosi

(1/2)kT

na cząsteczkę (zależy tylko od T).

Dla cząstek obracających się potrzeba 3 dodatkowych współrzędnych do opisania ruchu
(obrót względem trzech osi) więc mamy dodatkowe 3 stopnie swobody.
O ile dla N cząsteczek nie obracających się całkowita energia (wewnętrzna) U będzie
energią kinetyczną ruchu postępowego U = 3/2(NkT) to dla cząstek, które mogą obracać
się swobodnie we wszystkich kierunkach (wieloatomowe)

U = (3/2)(NkT) + (3/2)(NkT) = 3NkT

Natomiast dla cząstki dwuatomowej (gładkiej)

U = 3/2(NkT) + (2/2)(NkT) = (5/2)(NkT)

bo nie ma obrotu wokół osi hantli.
Zwróćmy uwagę, że mówimy tu o energii "ukrytej" (wewnętrznej) cząstek a nie o ener-
gii makroskopowej (związanej z ruchem masy). O tej energii mówiliśmy przy zasadzie
zachowania energii (energia indywidualnych cząstek nie zawarta w energii kinetycznej
czy potencjalnej ciała jako całości). Energię wewnętrzną oznacza się zazwyczaj przez U
i takie oznaczenie będziemy dalej stosować.

16.4 Pierwsza zasada termodynamiki

To jest po prostu inna wersja zasady zachowania energii, w której mamy rozdzieloną

energię ciała na część makroskopową i mikroskopową. Makroskopowa to energia ruchu
masy (energia mechaniczna). Mikroskopowa to "ukryta" energia cząstek (energia we-
wnętrzna).

Gdy dwa układy (ciała) o różnych temperaturach zetkniemy ze sobą to ciepło

∆

Q

przepływa z ciała cieplejszego do chłodniejszego. Zgodnie z zasadą zachowania energii,
ciepło pobrane przez układ musi być równe wzrostowi energii wewnętrznej układu plus
pracy wykonanej przez układ nad otoczeniem zewnętrznym czyli

∆

Q =

∆

U +

∆

W

(16.6a)

To jest sformułowanie

I zasady termodynamiki

.

Zasada ta pracuje "w obie strony" tzn., gdy nad układem zostanie wykonana praca to
układ może oddawać ciepło. To równanie bardzo często przybiera postać

dU = dQ – dW

(16.6b)

Z. Kąkol-Notatki do Wykładu z Fizyki

16-5

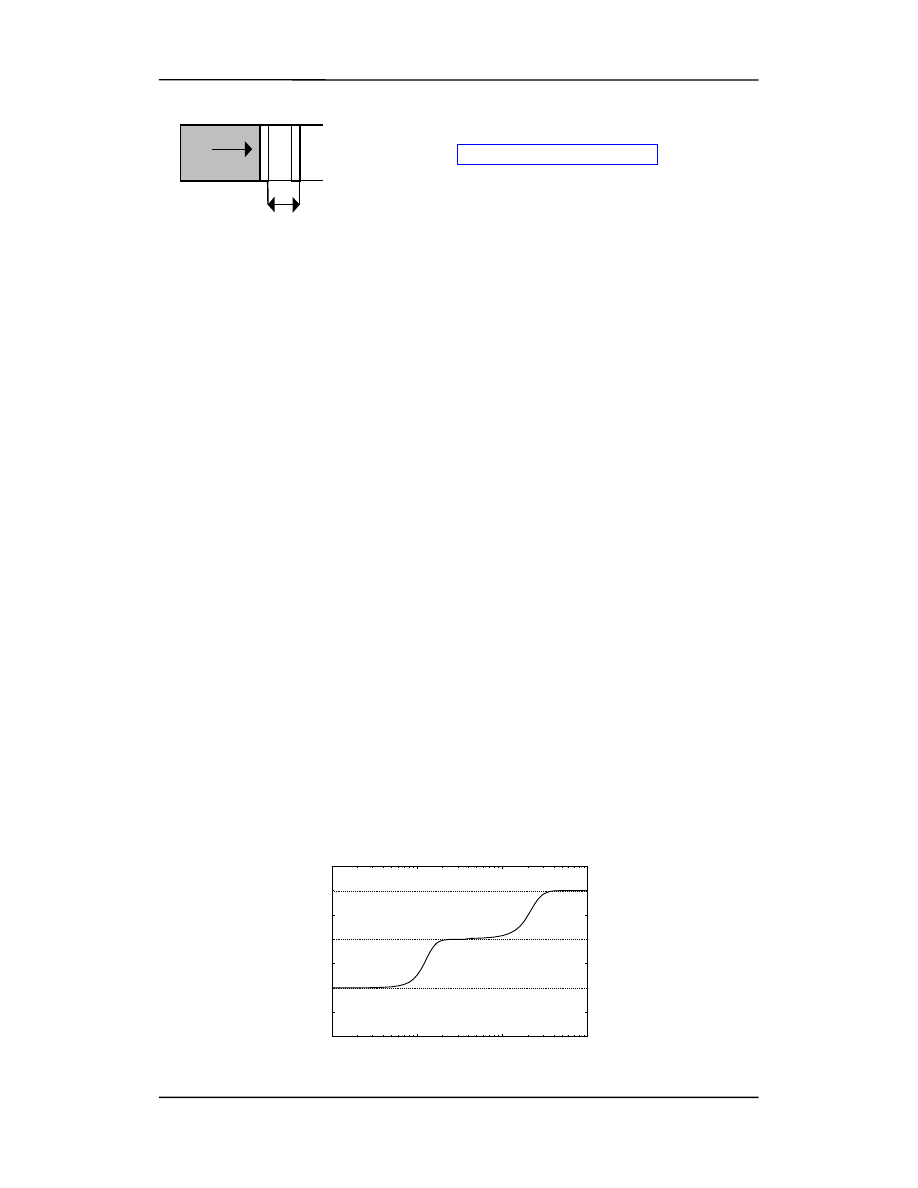
Jeżeli rozpatrujemy układ jak na rysunku obok to

dW = Fdl = (F/S)(Sdl) = pdV

(16.7)

i wtedy

dU = dQ – pdV

16.5 Ciepło właściwe

Ciepło właściwe definiujemy jako

dQ/dT

na gram lub mol substancji

(ciepło wago-

we lub molowe).

16.5.1 Ciepło właściwe przy stałej objętości

Ponieważ dV = 0 więc dU = dQ a stąd

c

v

= dQ/dT = dU/dT

Dla gazu jednoatomowego (dla jednego mola) U = (3/2)N

AV

kT = (3/2)RT.

Zatem

c

v

= (3/2)R

Dla cząsteczki dwuatomowej spodziewamy się więc

c

v

= (5/2)R

a dla wieloatomowej

c

v

= 3R

Niedoskonałością modelu opartego na mechanice klasycznej jest to, że przewiduje cie-
pło właściwe niezależne od temperatury, a badania pokazują, że jest to prawdziwe tylko
dla gazów jednoatomowych. Dla pozostałych c

v

rośnie z temperaturą.

Na rysunku poniżej przedstawiono c

V

dla wodoru (H

2

) w funkcji temperatury (w skali

logarytmicznej).

F

V

dl

S

10

100

1000

10000

2

4

6

8

(3/2) R

(5/2) R

(7/2) R

C

v

c

a

l/m

o

l K

Temperatra (K)

Z. Kąkol-Notatki do Wykładu z Fizyki

16-6

W temperaturach niższych od 100 K, c

v

= (3/2)R co wskazuje, że w tak niskich tempe-

raturach nie ma rotacyjnych stopni swobody. Rotacja staje się możliwa dopiero w tem-
peraturach wyższych (c

v

= (5/2)R). Ale w temperaturach powyżej 2000 K, c

v

osiąga

wartość (7/2)R.
Wytłumaczenie tych zjawisk nie jest możliwe na gruncie mechaniki klasycznej. Dopie-
ro mechanika kwantowa daje wyjaśnienie tych zmian. Gdyby cząstka miała moment
pędu to musiał by on być równy co najmniej L

min

= h/2

π

≈

10

-34

kg m

2

s

-1

(analogia do

modelu Bohra atomu wodoru). Energia kinetyczna ruchu obrotowego dana jest wyraże-
niem

I

L

I

E

rot

2

2

2

2

=

=

ω

Dla cząsteczki H

2

m=1.67·10

-27

kg a R

≈

5·10

-11

m, więc I = 2mR

2

≈

8.3·10

-48

kg m

2

.

Ponieważ na jeden stopień swobody przypada energia kT/2 więc

kT/2 = L

2

/2I

czyli

T = L

2

/kI

Stąd dla L

min

otrzymujemy T

min

≈

90 K.

Dla niższych temperatur energia jest za mała aby wzbudzić rotacje co wymaga pewnej
minimalnej energii. Podobnie jest dla ruchu drgającego, który także jest skwantowany.
E

drg,min

= hv. Dla typowej cząsteczkowej częstotliwości drgań 10

14

Hz (zakres widzial-

ny) otrzymujemy energię drgań

≈

6·10

-20

J co odpowiada temperaturze około 4000 K.

Tak więc z zasady ekwipartycji energii wynika, że w tak wysokich temperaturach śred-
nia energia drgań E

drg

= kT/2. Oprócz energii kinetycznej tego ruchu istnieje jeszcze je-

go energia potencjalna. Zatem średnia energia wewnętrzna na cząsteczkę wynosi

U = E

śr,kin,post

+ E

śr,kin,rot

+ E

śr,kin,drg

+ E

śr,pot,drg

U = (3/2)kT + (2/2)kT + (1/2)kT + (1/2)kT = (7/2)kT

Dla 1 mola

U = (7/2)RT więc c

v

= (7/2)R

16.5.2 Ciepło właściwe przy stałym ciśnieniu

Z I zasady termodynamiki mamy

dQ = dU + pdV

Ponieważ U zależy tylko od T więc mamy dU = c

v

dT więc

dQ = c

v

dT + pdV

Z. Kąkol-Notatki do Wykładu z Fizyki

16-7

Dla gazu doskonałego (1 mola) dV = RdT/p, więc

dQ = c

v

dT + RdT

skąd

dQ/dT = c

v

+ R

Ostatecznie więc

c

p

= c

v

+ R

Molowe ciepła właściwe różnych rodzajów gazów doskonałych (teoretyczne) są zesta-
wione w tabeli poniżej.

Typ gazu

c

v

c

p

c

p

/c

v

Jednoatomowy
Dwuatomowy + rotacja
Dwuatomowy + rotacja + drgania
Wieloatomowy + rotacja (bez drgań)

(3/2)R
(5/2)R
(7/2)R
(6/2)R

(5/2)R
(7/2)R
(9/2)R
(8/2)R

5/3
7/5
9/7
4/3

16.6 Rozprężanie izotermiczne

Działanie silnika opiera się o rozprężanie zapalonej mieszanki gazowej.

Zwykle dwa przypadki

•

rozprężanie izotermiczne

•

rozprężanie adiabatyczne

Przy rozprężaniu izotermicznym trzeba utrzymywać stałą temperaturę ścian cylindra,
czyli tłok musi poruszać się wolno, żeby gaz mógł pozostawać w równowadze termicz-
nej ze ściankami cylindra.
Ponieważ T = const. więc dU = 0, a stąd dQ = dW









=

=













=

=

∆

=

∆

∫

∫

∫

1

2

1

ln

d

d

d

2

2

1

2

1

V

V

NkT

v V

V

NkT

V

V

NkT

V

p

W

Q

V

V

V

V

V

(16.8)

16.7 Rozprężanie adiabatyczne

Zwykle w silnikach tłok porusza się bardzo szybko więc nie ma dość czasu na prze-

pływ ciepła pomiędzy gazem a ścianami cylindra. Wtedy dQ = 0 i otrzymujemy

dU + pdV = 0

Możemy to przepisać w postaci

c

v

dT + pdV = 0

na 1 mol.
Z równania stanu gazu doskonałego otrzymujemy różniczkując

pdV + Vdp = RdT

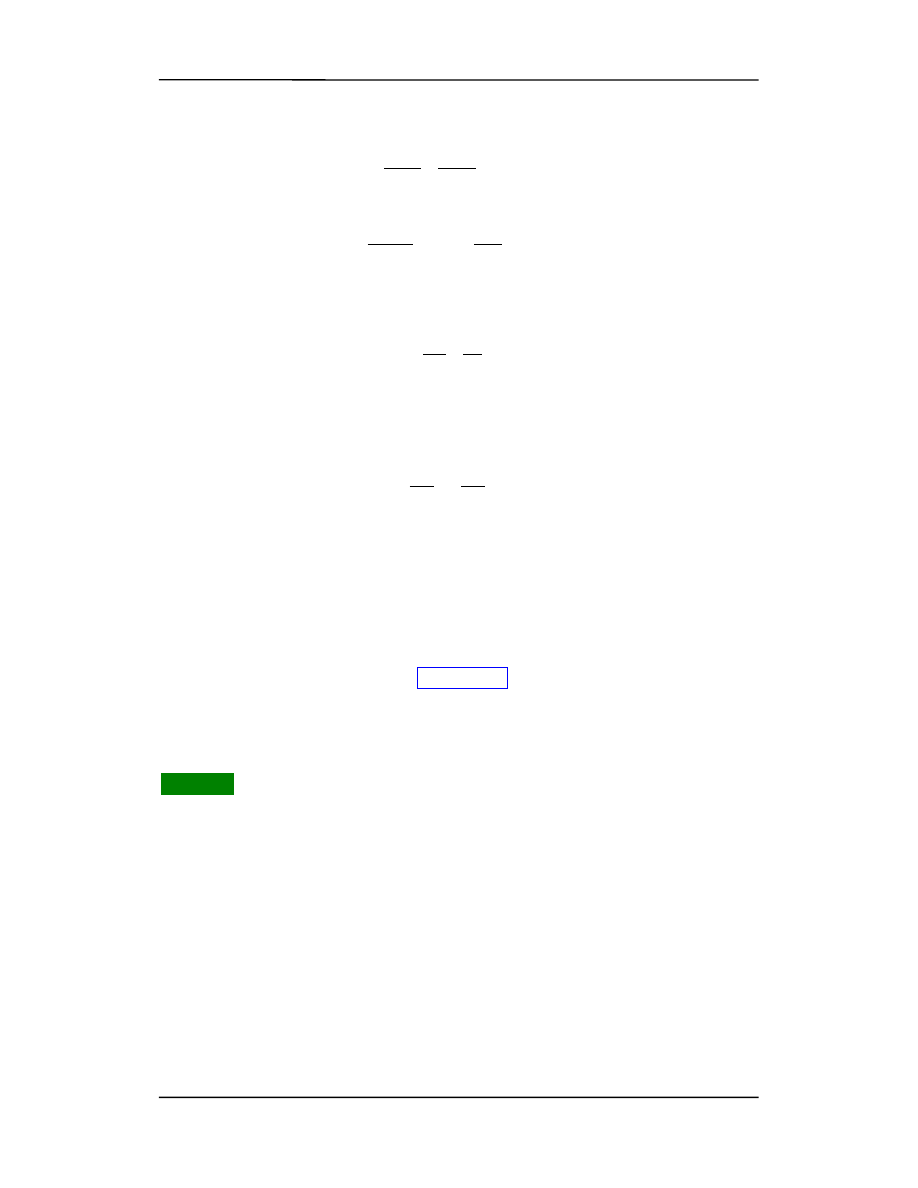
Z. Kąkol-Notatki do Wykładu z Fizyki

16-8

Stąd obliczmy dT i wstawiamy do poprzedniego równania

0

d

d

0

d

d

d

=

+













+

=

+













+

p

R

V

c

V

p

R

R

c

V

p

R

p

V

R

V

p

c

v

v

v

Zastępujemy teraz c

v

+ R = c

p

i otrzymujemy

0

d

d

=

+

p

p

V

V

γ

gdzie

γ = c

p

/c

v

.

Całkując to równanie otrzymamy

.

const

ln

ln

0

d

d

=

+

=

+

∫

∫

p

V

p

p

V

V

γ

γ

gdzie const. oznacza stałą całkowania.
Mamy więc

ln(pV

γ

) = const.

czyli

pV

γ

= const.

(16.9)

co można zapisać:

p

1

V

1

γ

= p

2

V

2

γ

Przykład 1

Silnik benzynowy ma stopień sprężu 9 tzn. V

2

/V

1

= 9. Jaki jest stosunek temperatury

gazów wydechowych do temperatury spalania?

p

1

V

1

γ

= p

2

V

2

γ

więc p

2

/p

1

= (V

1

γ

/V

2

γ

)

Dla gazu doskonałego

p

2

/p

1

= (V

1

T

2

)/(V

2

T

1

)

Porównują te równania otrzymujemy

T

2

/T

1

= (V

1

/V

2

)

γ-1

Powietrze jest głównie dwuatomowe więc

γ = 1.4. Stąd otrzymujemy T

2

/T

1

= 0.415