Do wglądu nie drukować!!!

Do wglądu nie drukować!!!

1

I TD

12.12.2006

Laboratorium z fizyki

Ćw. nr : 46

Wyznaczanie stałej siatki dyfrakcyjnej

Tomasz Wojnar

L

5

Do wglądu nie drukować!!!

Do wglądu nie drukować!!!

2

1. Wstęp teoretyczny:

Fale powstają w wyniku wychylenia fragmentu ośrodka sprężystego z normalnego położenia,
równowagi, co w następstwie powoduje drgania fragmentu wokół tego położenia. Dzięki
sprężystym właściwościom ośrodka drgania te są przekazywane kolejno coraz dalszym
częściom jego ośrodka i w ten sposób powstaje zaburzenie inaczej mówiąc ruch falowy. Do
rozchodzenia się fal mechanicznych niezbędny jest ośrodek materialny natomiast do
przenoszenia fal elektromagnetycznych taki ośrodek nie jest potrzebny, własności ośrodka
decydują o prędkości rozchodzenia się fal w nim.

Rodzaje fal.
Fale możemy rozróżnić obserwując, jaki kąt tworzy kierunek cząstek materii z kierunkiem
rozchodzenia się samych fal, gdy ruch cząstek materii przenoszącej falę są prostopadłe do
kierunku rozchodzenia się tej fali wówczas mamy do czynienia z falą poprzeczną.
Fale świetlne nie są falami mechanicznymi przemieszczające się tu zaburzenie nie jest
związane z ruchem materii, lecz ze zmianami pola elektromagnetycznego. Fale świetlne są
również falami porzecznymi. Jeżeli cząstki przenoszące falę mechaniczną poruszają się od
przodu do tyłu wzdłuż kierunku rozchodzenia się fali wówczas mamy do czynienia z falą
podłużną. Fale można rozróżniać na fale uzależnione od liczby wymiarów niezbędnych do
opisu kierunku rozchodzenia energii: jedno, dwu oraz trójwymiarowe.
Jeżeli zburzenie rozchodzi się tylko w jednym kierunku falę taką nazywamy falą płaską.
Innym przykładem fali jest fala kulista, tutaj zaburzenie rozchodzi się we wszystkich
kierunkach wychodzących z punktu będącego środkiem fali.

Superpozycja fal.
Zasada superpozycji mówi, że każde nawet najbardziej złożone zaburzenie można
przedstawić jako wynik liniowego składania prostych fal sinusoidalnych o różnych
wartościach amplitudy różnej fazie początkowej, których częstotliwości tworzą ciąg
liczbowy:
f, 2f, 3f... nf f- jest to częstotliwość podstawowa
2f –wyższe harmoniczne

Interferencja fal.
Warunki: obie fale muszą mieć te same częstotliwości, te same długości fal oraz różnica faz
początkowych musi być stałą wielkością.





n

2





wzmocnienie fal A=max





)

1

2

(







n

wygaszenie fali A=0

Dyfrakcja fal.
Dyfrakcja polega na wyraźnym odchyleniu od prostoliniowości rozchodzenia się fali, kiedy
przechodzi przez nie wielkie otwory czy szczeliny. Każdy punkt ośrodka, do którego dociera
fala staje się źródłem nowej fali kulistej. Dyfrakcją światła nazywamy zjawisko ugięcia się
fali świetlnych na krawędzi przeszkody i zachodzeniu światła w obszar cienia
geometrycznego

Siatka dyfrakcyjna
Siatka dyfrakcyjna jest dokładnie wyszlifowaną płytką szklaną, na której za pomocą
diamentowego ostrza nakreślono równoodległe i równoległe rysy stanowiące odpowiedni
przysłon. Zastosowanie specjalnych urządzeń pozwala na otrzymanie stałej odległości
pomiędzy rysami, odległość ta nosi nazwę stałej siatki.

Do wglądu nie drukować!!!

Do wglądu nie drukować!!!

3

2. Wykonanie ćwiczenia:

- Cel ćwiczenia:

Celem ćwiczenia jest wyznaczenie stałej siatki dyfrakcyjnej użytej w doświadczeniu.

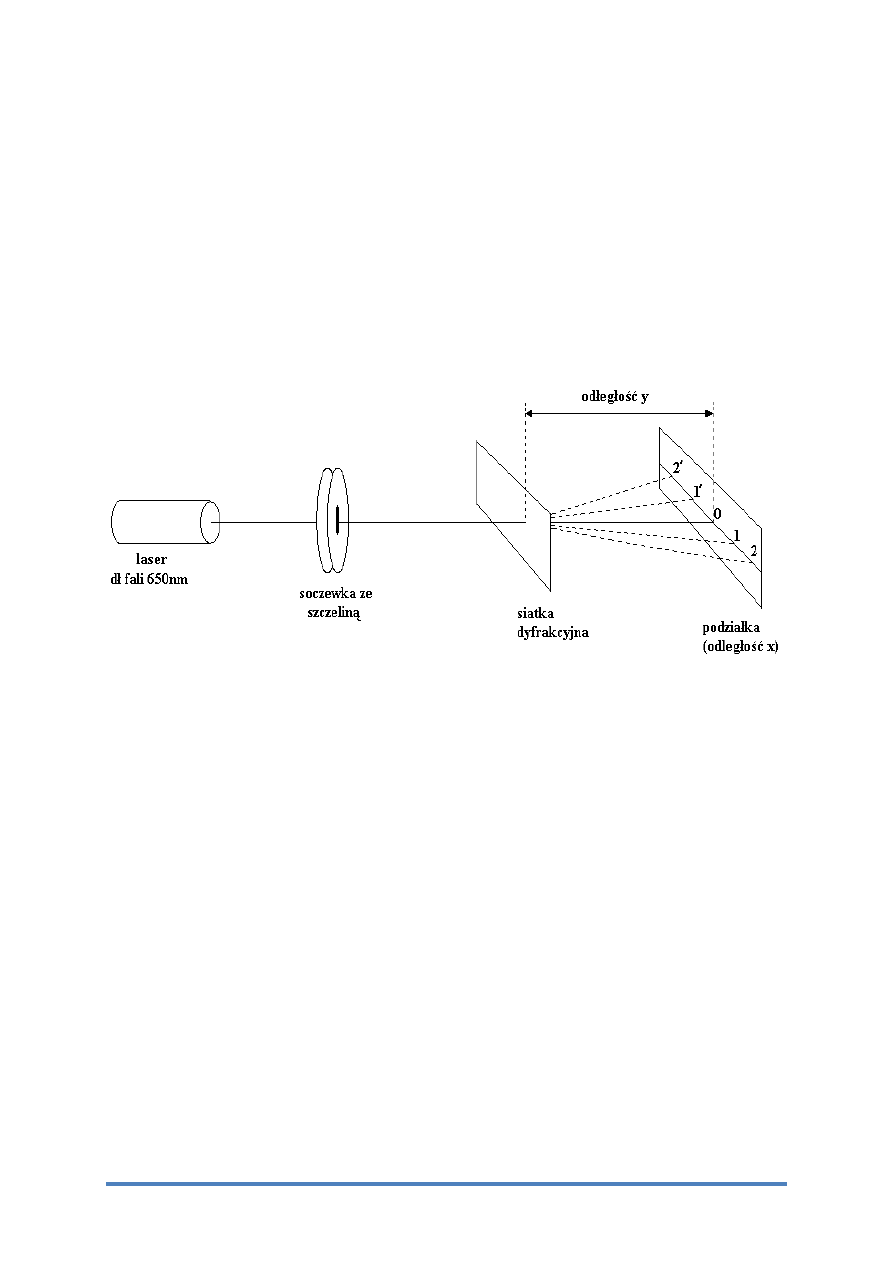
- Schemat układu pomiarowego:

Rysunek 1

- Opis wykonania pomiarów:

Po zmontowaniu układu pomiarowego jak na rysunku 1, ustawiamy siatkę dyfrakcyjną
najbliżej soczewki i zapisujemy odległość siatki od ekranu (pomiar wartości y),
obserwujemy prążki. Następnie mierzymy odległości poszczególnych prążków rzędu 1 i
2 od prążka zerowego(pomiar wartości x). Po pomiarze przesuwamy siatkę dyfrakcyjną
o 5mm w stronę ekranu i powtarzamy pomiary analogicznie do poprzedniej sytuacji.

- Lista wykorzystanych przyrządów:

Laser monochromatyczny o λ = 650 nm.
Układ optyczny składający się z 2 soczewek, szczeliny, siatki dyfrakcyjnej (badany
element) i ekranu.
2 podziałki liniowe.

Do wglądu nie drukować!!!

Do wglądu nie drukować!!!

4

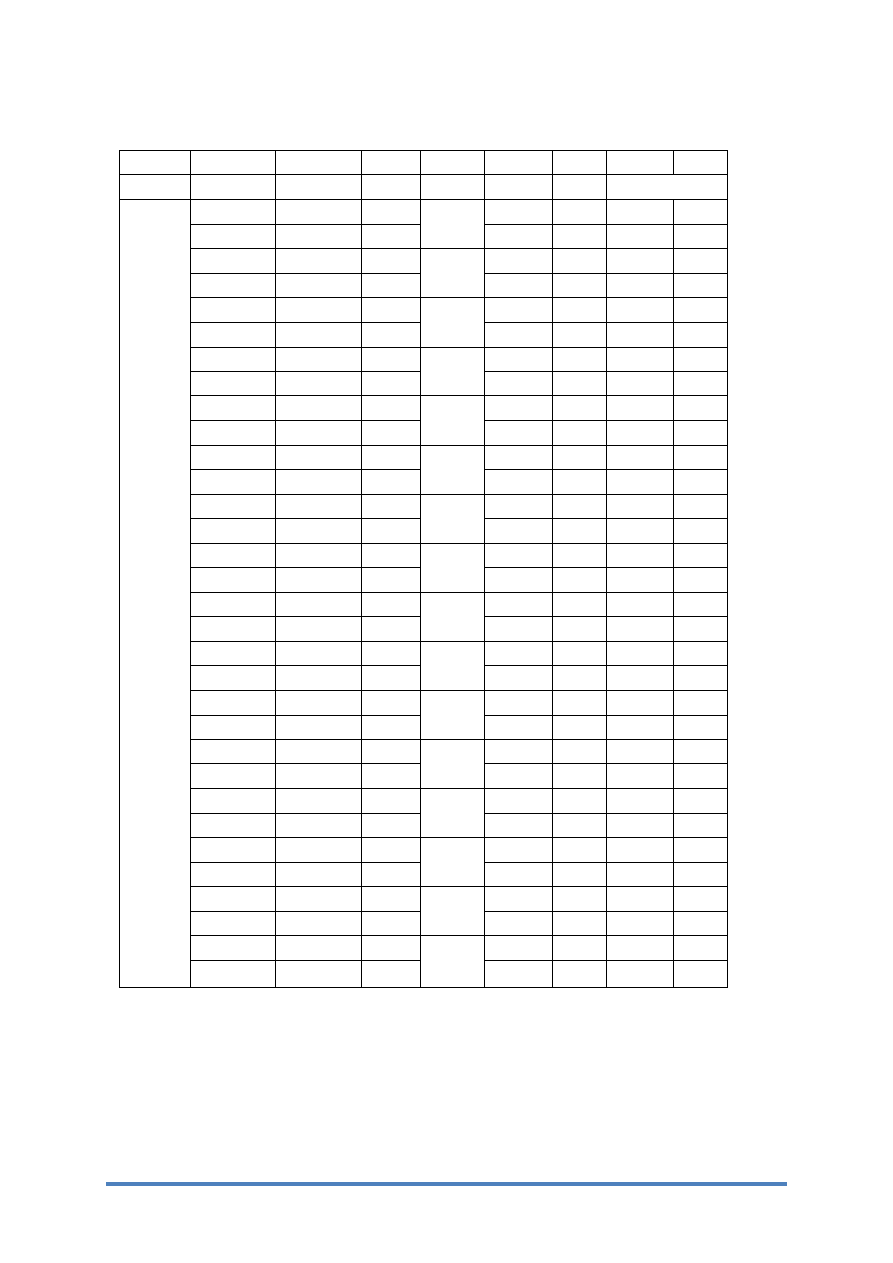
3. Tabela z wynikami pomiarów:

λ

k

x

k

∆x

y

∆y

sinφ

d

∆d

[nm]

-

[cm]

[cm] [cm]

[cm]

-

[m * 10

-9

]

650

1

1,6

0,1

13

0,1

0,122

5,32

0,39

2

3,1

0,1

0,1

0,232

5,60

0,14

1

1,6

0,1

14

0,1

0,114

5,73

0,41

2

3,3

0,1

0,1

0,229

5,67

0,13

1

1,7

0,1

15

0,1

0,113

5,77

0,39

2

3,5

0,1

0,1

0,227

5,72

0,13

1

1,8

0,1

16

0,1

0,112

5,81

0,38

2

3,6

0,1

0,1

0,220

5,92

0,13

1

1,9

0,1

17

0,1

0,111

5,85

0,36

2

4,1

0,1

0,1

0,234

5,55

0,11

1

2,1

0,1

18

0,1

0,116

5,61

0,32

2

4,3

0,1

0,1

0,232

5,60

0,11

1

2,2

0,1

19

0,1

0,115

5,65

0,31

2

4,5

0,1

0,1

0,230

5,64

0,11

1

2,4

0,1

20

0,1

0,119

5,46

0,28

2

4,7

0,1

0,1

0,229

5,68

0,10

1

2,5

0,1

21

0,1

0,118

5,50

0,27

2

5,1

0,1

0,1

0,236

5,51

0,10

1

2,6

0,1

22

0,1

0,117

5,54

0,26

2

5,2

0,1

0,1

0,230

5,65

0,10

1

2,7

0,1

23

0,1

0,117

5,58

0,26

2

5,5

0,1

0,1

0,233

5,59

0,09

1

2,7

0,1

24

0,1

0,112

5,81

0,27

2

5,5

0,1

0,1

0,223

5,82

0,10

1

2,8

0,1

25

0,1

0,111

5,84

0,26

2

5,8

0,1

0,1

0,226

5,75

0,09

1

3,0

0,1

26

0,1

0,115

5,67

0,24

2

6,0

0,1

0,1

0,225

5,78

0,09

1

3,2

0,1

27

0,1

0,118

5,52

0,22

2

6,4

0,1

0,1

0,231

5,64

0,09

1

3,3

0,1

28

0,1

0,117

5,55

0,22

2

6,8

0,1

0,1

0,236

5,32

0,39

k - rząd prążka
x

k

- odległość prążka od prążka zerowego , ∆x- niepewność odczytu wartości x

k

y – odległość siatki dyfrakcyjnej od ekranu
d – stała siatki dyfrakcyjnej

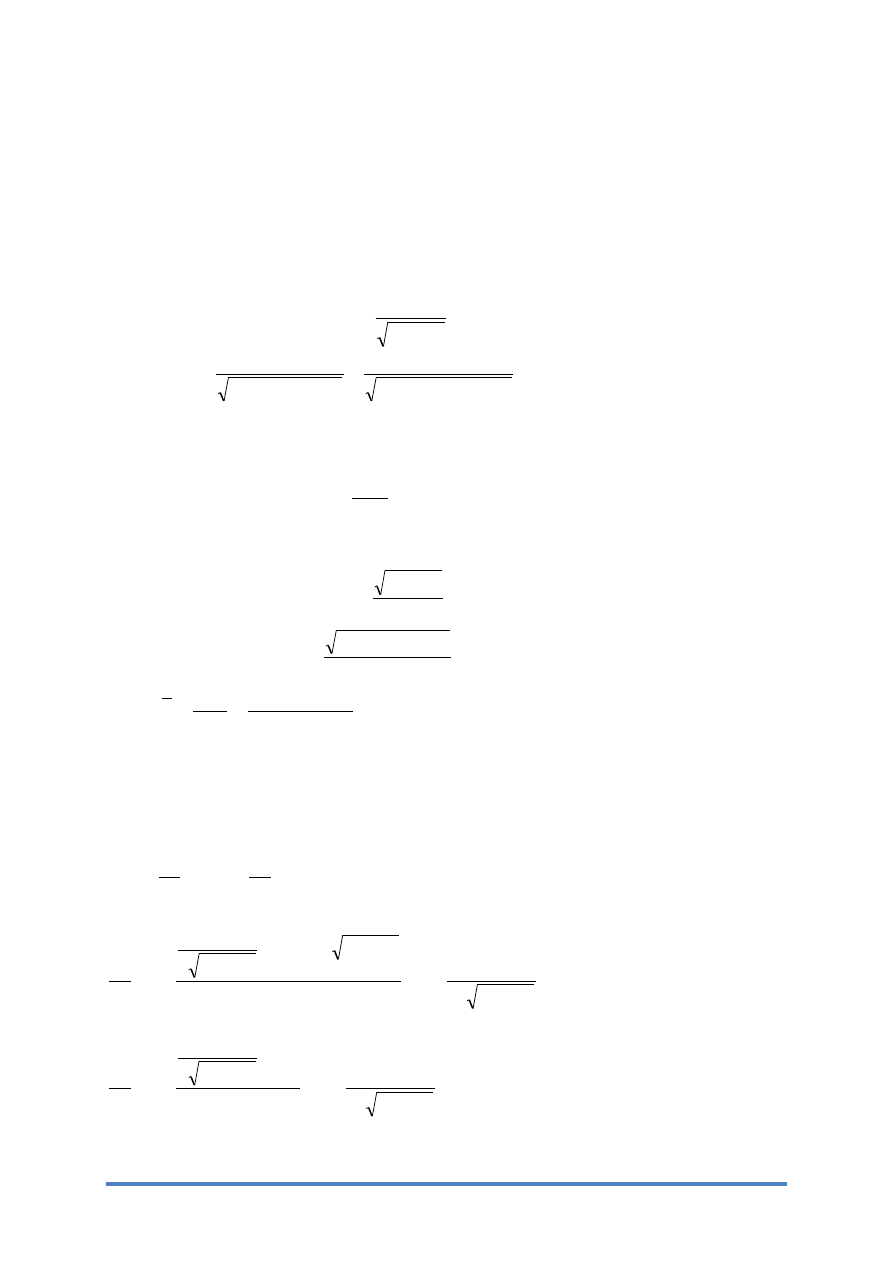
Do wglądu nie drukować!!!

Do wglądu nie drukować!!!

5

4. Obliczenia:

- Obliczenia szukanych wartości:

Większość obliczeń zostało wykonanych w arkuszu kalkulacyjnym z powodu
większej szybkości obliczeń. Jedynie przykładowe obliczenia zostały zapisane.

Obliczmy sinφ ze wzoru:

2

2

sin

y

x

x

















2

2

2

2

169

56

,

2

6

,

1

13

6

,

1

6

,

1

sin

cm

cm

cm

cm

cm

cm



0,122

Następnie obliczamy stałą siatki dyfrakcyjnej ze wzoru:





sin

k

d



Więc po podstawieniu wzoru na sinφ trzymujemy:

2

2

2

k

k

x

x

y

k

d















2

2

2

9

6

,

1

13

6

,

1

*

10

*

650

*

1

cm

cm

cm

m

d

5,33*10

-6

m = 5,33µm







32

d

d





32

10

180838

-9

m

5,65*10

-6

m = 5,65µm

- Analiza niepewności pomiarowych:

Wyprowadzenie wzoru na ∆d metodą różniczki zupełnej:















































y

y

d

x

x

d

d

2

2

2

2

2

2

2

2

2

2

2

1

y

x

x

y

x

y

x

x

x

y

x

x

d





























2

2

2

2

2

2

2

2

1

y

x

x

yx

x

yx

y

x

y

d























Do wglądu nie drukować!!!

Do wglądu nie drukować!!!

6







d

y

x

x

y

x

yx

x

x

y

y

 





 









2

2

2

2

2

2

2

















cm

cm

cm

cm

cm

cm

cm

cm

cm

cm

cm

cm

m

d

1

,

0

*

13

6

,

1

6

,

1

6

,

1

*

13

10

*

650

1

,

0

*

13

6

,

1

6

,

1

13

*

10

*

650

2

2

2

9

2

2

2

2

9

0

,

37*10

-6

m = 0,37µm

Średnie ∆d liczymy ze wzoru:











32

d

d

0,20*10

-6

m = 0,20µm

5. Wnioski:

Wyznaczona wartość stałej siatki dyfrakcyjnej jest obarczona dosyć małą niepewnością
pomiarową nieprzekraczającą 7,5%. Więc możemy stwierdzić, że ćwiczenie zostało
wykonane dosyć dokładnie.
Wyznaczona stała siatki dyfrakcyjnej d=5,65±0,20*10

-6

m = 5,65±0,20µm jest jedną z

wielkości charakteryzującą użytą siatkę dyfrakcyjną. Można zauważyć, jeśli obserwujemy
plamkę wyższego rzędu, lub dalej od siatki dyfrakcyjnej umieścimy ekran to możemy
znacznie zmniejszyć niepewność, z jaką wyznaczamy stałą siatki dyfrakcyjnej.