Termodynamika Techniczna

Seminarium II

Zagadnienia:

Lepkość dynamiczna i kinematyczna, liczba Reynoldsa,
równanie Bernoulliego, gazy doskonałe, gazy rzeczywiste,
równanie Clapeyrona, prawa gazowe, termiczne równanie
stanu gazów, prawo Avogadra, równanie van der Waalsa

.

2

2

const

g

h

w

p

s

















Równanie Bernoulliego:

Przy ustalonym przepływie w dowolnym przekroju rurociągu suma ciśnienia statycznego , dynamicznego
i ciśnienia położenia (wysokości) jest wielkością stałą

h – wysokość położenia [m]
ρ – gęstość czynnika [kg/m

3

]

p

s

– ciśnienie statyczne [Pa]

w – prędkość przepływu [m/s]
g – przyśpieszenie ziemskie 9,81 [m/s

2

]

Równanie Bernoulliego

Termodynamika gazów

Gaz doskonały

 brak oddziaływań międzycząsteczkowych z wyjątkiem odpychania
w momencie zderzeń cząsteczek
 objętość cząsteczek jest znikoma w stosunku do objętości gazu
 zderzenia cząsteczek są doskonale sprężyste

Gaz półdoskonały

 w drobinach gazu występują drgania

Gaz rzeczywisty

 zachowuje się jak półdoskonały pod dostatecznie niskim ciśnieniem

Prawo Boyle’a-Mariotte’a

Dotyczy zachowania gazu doskonałego w przemianie izotermicznej

Ciśnienie danej masy gazu jest odwrotnie proporcjonalne do zajmowanej

objętości w danej temperaturze

R. Boyle 1662 r., E. Mariotte 1676 r.

T=const.; p·V = const.

p

V

1

~

2

2

1

1

V

p

V

p







1

2

2

1

V

V

p

p



Prawo Gay-Lussaca

.

0

0

const

T

V

T

V





Przy stałym ciśnieniu objętość danej masy jest wprost

proporcjonalna do temperatury

Prawo Charlesa

Dotyczy zachowania gazu doskonałego w przemianie izochorycznej.

W stałej objętości ciśnienie danej masy gazu jest wprost proporcjonalne do

temperatury

T

p~

.

0

0

const

T

p

T

p





Prawo Avogadra

W tych samych warunkach fizycznych

tj. w takiej samej temperaturze i pod takim samym ciśnieniem,

w równych objętościach różnych gazów

znajduje się taka sama liczba cząstek

W warunkach normalnych (1 atm., 0

o

C)

1 mol

dowolnego gazu zajmuje objętość

22,4 dm

3

W warunkach umownych (1 bar, 0

o

C)

1 mol

gazu będzie zajmował objętość

22,71 dm

3

Równanie Clapeyrona

 gaz doskonały składa się z cząsteczek stanowiących punkty materialne,
a więc, nie posiadających objętości własnej
 pomiędzy poszczególnymi cząsteczkami nie istnieją siły wzajemnego
oddziaływania (przyciągania lub odpychania).

Gaz rzeczywisty będzie spełniał wyżej wymienione warunki w przypadku, gdy:
lub

Równanie stanu gazu doskonałego

(równanie Clapeyrona)

,

może zostać

zapisane w jednej z postaci:

gdzie:

- indywidualna stała gazowa

- objętość właściwa

0



p





V

nRT

pV 

T

mR

pV

i



T

R

pv

i



]

[

kgK

J

M

R

R

i



]

[

3

kg

m

m

V

v 

Prawo Daltona

Ciśnienie p

i

, wytworzone w naczyniu przez jakiś komponent (składnik

„i”) jest równe ciśnieniu, jakie wytworzyłby ten składnik, gdyby sam
wypełniał całe naczynie. Jest to tzw.

ciśnienie cząstkowe

.

Dla dostatecznie rozrzedzonych gazów, ciśnienie gazowej mieszaniny
(p) jest równe sumie ciśnień cząstkowych poszczególnych składników:

p = p

1

+ p

2

+…+ p

n

„gaz widzi ścianki, a nie widzi drugiego gazu”

Stąd równanie Clapeyrona można zapisać jako:

RT

M

m

M

m

M

m

pV

i

i

)

...

(

2

2

1

1









lub

RT

n

n

n

pV

i

)

...

(

2

1









gdzie: n

i

– liczba moli składnika mieszaniny

Ciepło właściwe gazów doskonałych

Mianem ciepła właściwego określa się ilość ciepła, jaka jest niezbędna

do ogrzania jednostki (masy, objętości, liczby moli) substancji o 1 K

gdzie: c – ciepło właściwe, Q – zmiana ciepła (energii), m – masa,
T – zmiana temperatury

]

[

kgK

J

T

m

Q

c







]

[J

T

c

m

Q











Ciepło właściwe

Ciepło właściwe

(pojemność cieplna, heat capacity) danej substancji jest

zdefiniowana jako pochodna ciepła wymienianego przez układ z otoczeniem,
względem temperatury:

]

,

[

kmolK

J

kgK

J

dT

dq

c 

gdzie:

]

,

[

kmol

J

kg

J

q

-jednostkowa ilość ciepła (odniesiona do
jednostkowej ilości czynnika)

Ciepło właściwe ciał stałych i cieczy, a w pewnych warunkach również
gazów, jest wielkością w przybliżeniu stałą, zatem:

]

,

[

kmolK

J

kgK

J

T

q

c





Ciepło właściwe

Ciepło właściwe:

 masowe c [J/kgK]

 molowe C [J/kmolK]

zależność: C=c∙M

Wielkość ciepła właściwego jest uzależniona od rodzaju przemiany, jakiej
podlega czynnik, czyli od sposobu, w jaki wymieniane jest ciepło:

 ciepło właściwe przy stałej objętości:

 ciepło właściwe przy stałym ciśnieniu:

V

v

T

U

c



















p

p

p

T

I

T

H

c





































U- energia wewnętrzna,
H- entalpia (oznaczana również jako I)

Ciepło właściwe

Zależności wiążące wyżej zdefiniowane wielkości:







v

p

v

p

C

C

c

c

gdzie: κ - wykładnik adiabaty

Równanie Mayera:

ind

v

p

R

c

c





wynikające zależności:

1







ind

v

R

c

ind

p

R

c

1









R

C

C

v

p





R

c

v

2

3



Zależności wartości ciepła właściwego dla gazów:

- jednoatomowych

R

c

p

2

5



R

c

v

2

5



- dwuatomowych

R

c

p

2

7



R

c

v

3



- trój- i wieloatomowych

R

c

p

4



Ciepło właściwe

Ciepło właściwe gazu rzeczywistego nie jest wielkością stałą – zależy ono od
wielu parametrów, z których najistotniejszym jest temperatura: c =c(T).
W pewnych warunkach dogodnym sposobem posługiwania się ciepłem
właściwym gazu rzeczywistego jest obliczenie jego wartości średniej w
rozważanym zakresie temperatur:







2

1

)

(

1

2

T

T

śr

dT

T

c

T

T

c

c

Mając do dyspozycji wartości średniego ciepła właściwego, określonego od
T

0

(najczęściej T

0

= 0 ) do danej temperatury, średnie ciepło właściwe w

zakresie temperatur T

1 ,

T

2

można określić z zależności:

1

2

1

2

1

0

2
0

2

1

|

|

|

T

T

T

c

T

c

c

T
T

T
T

T
T











Ciepło właściwe gazów półdoskonałych

Jeżeli w danym procesie zmiany temperatur stanów początkowego
i końcowego są niewielkie, można przyjąć, że zmiana ciepła właściwego jest
niewielka

Zmiany temperatur układu podczas ogrzewania lub chłodzenia
gazów półdoskonałych układu są stosunkowo duże:

)

(

1

2

2

1

,

2

1

T

T

c

m

cdT

m

Q

T

T

c

















)

(

|

)

(

1

2

2

1

,

2

1

2

1

T

T

c

m

dT

T

c

m

Q

T
T

T

T

c



















Właściwości gazów rzeczywistych

Gazy rzeczywiste różnią się od gazów doskonałych tym, że ich cząsteczki
posiadają własną objętość oraz oddziałują na siebie siłami
międzycząsteczkowymi (zwanymi siłami van der Waalsa)

Równanie van der Waalsa:

 dla 1 kilomola gazu

 dla n kilomoli

gdzie: V’ - molowa objętość gazu, V’ =V/n [m

3

/kmol]

V - objętość gazu
a – stała charakterystyczna dla danego gazu uwzględniająca
przyciąganie cząsteczek gazu czyli spadek ciśnienia
b - stała charakterystyczna dla danego gazu uwzględniająca objętość
własną cząsteczek

T

R

b

V

V

a

p









)

'

)(

'

(

2

T

R

n

b

n

V

V

a

n

p















)

)(

(

2

2

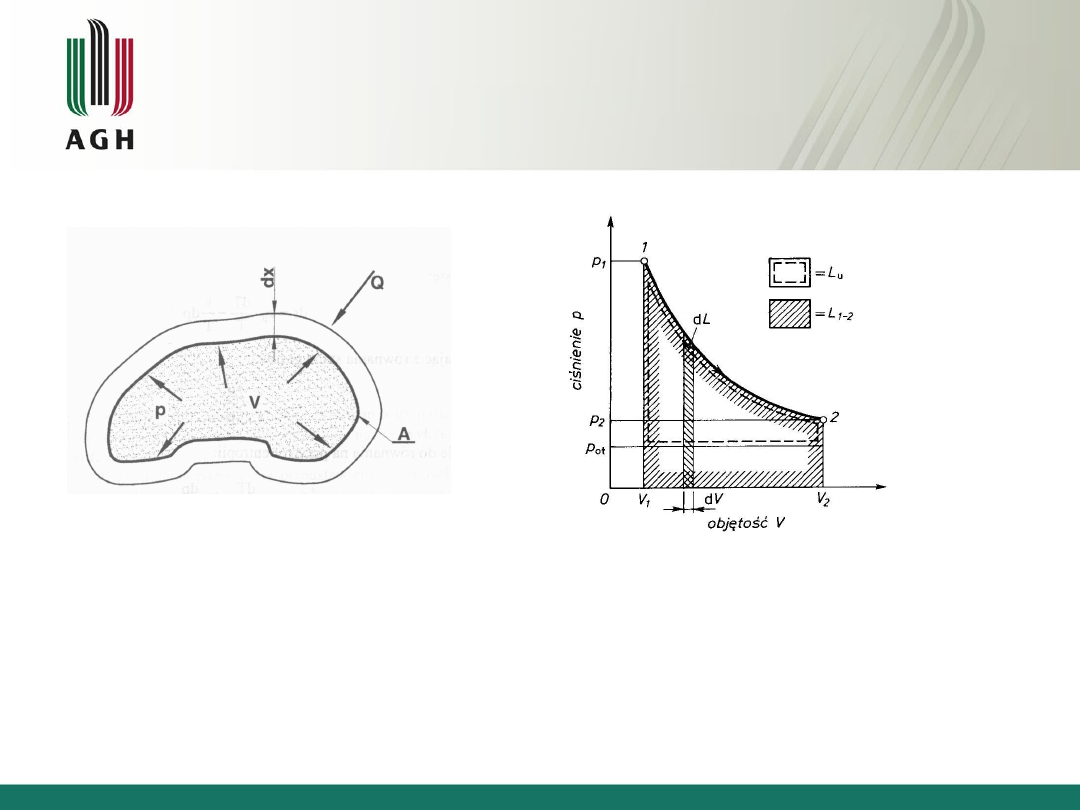
Praca bezwzględna

Jeżeli w układzie o objętości V ograniczonym elastyczną powłoką znajduje się gaz o
ciśnieniu bezwzględnym p, a pod wpływem doprowadzonego ciśnienia objętość V
zwiększy się o dV, to wykonaną podczas tego rozprężania gazu pracę powierzchni A przy
ciśnieniu p na drodze dx określa się mianem pracy bezwzględnej

pdV

dx

A

p

L











p – ciśnienie bezwzględne gazu
A – powierzchnia, na której wykonywana
jest praca
dx – droga, na której wykonywana jest praca
dV – przyrost objętości





2

1

V

V

pdV

I

Zależność dla przemiany zachodzącej
w granicach zmian objętości od V

1

do V

2

dla 1 kg czynnika

Praca bezwzględna:

.

0

0

const

T

V

T

V





Przy stałym ciśnieniu objętość danej masy jest
wprost proporcjonalna do temperatury

Prawo Gay-Lussaca:

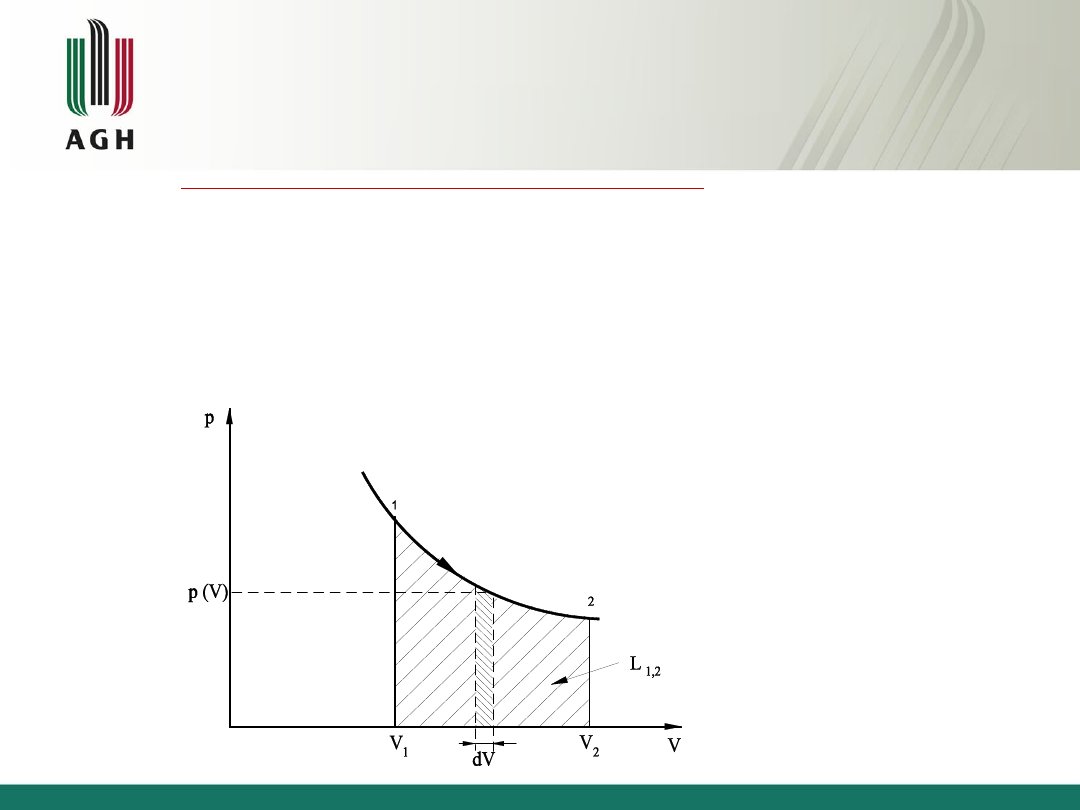
Praca

Praca zewnętrzna (związana ze zmianą objętości)

Praca zewnętrzna oddawaną do otoczenia przez układ przyjmuje się za
dodatnią (dV>0), a pracę zewnętrzną pobieraną przez układ z otoczenia za
ujemną (dV<0).

W szczególnym przypadku praca zewnętrzna ogranicza się do pracy zmiany
objętości, a wtedy dla przemian odwracalnych ciał prostych mamy:





2

1

2

,

1

V

V

pdV

L

pdV

dU

dQ





















2

1

1

2

2

,

1

1

2

2

,

1

V

V

pdV

U

U

L

U

U

Q

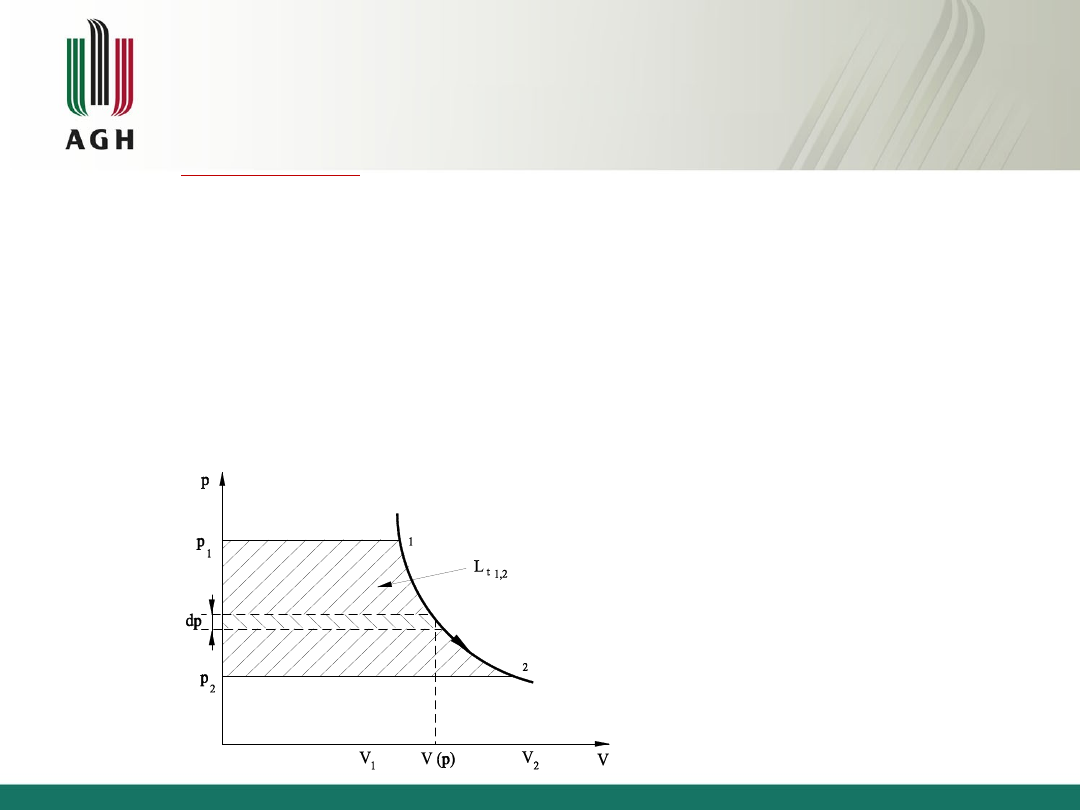
Praca

Praca techniczna

Praca techniczna jest dodatnia przy rozprężaniu (dp<0) i ujemna przy
sprężaniu (dp>0)

Jeżeli w równaniu

wyrażającym pierwszą zasadę termodynamiki dla układu zamkniętego,
wstawimy w miejsce energii wewnętrznej entalpię, wówczas praca zewnętrzna
zamieni się na

pracę techniczną

i dla przemian odwracalnych równanie to

przyjmie postać:







2

1

2

,

1

p

p

t

Vdp

L

pdV

dU

dQ



















2

1

1

2

2

,

1

1

2

2

,

1

p

p

t

Vdp

I

I

L

I

I

Q

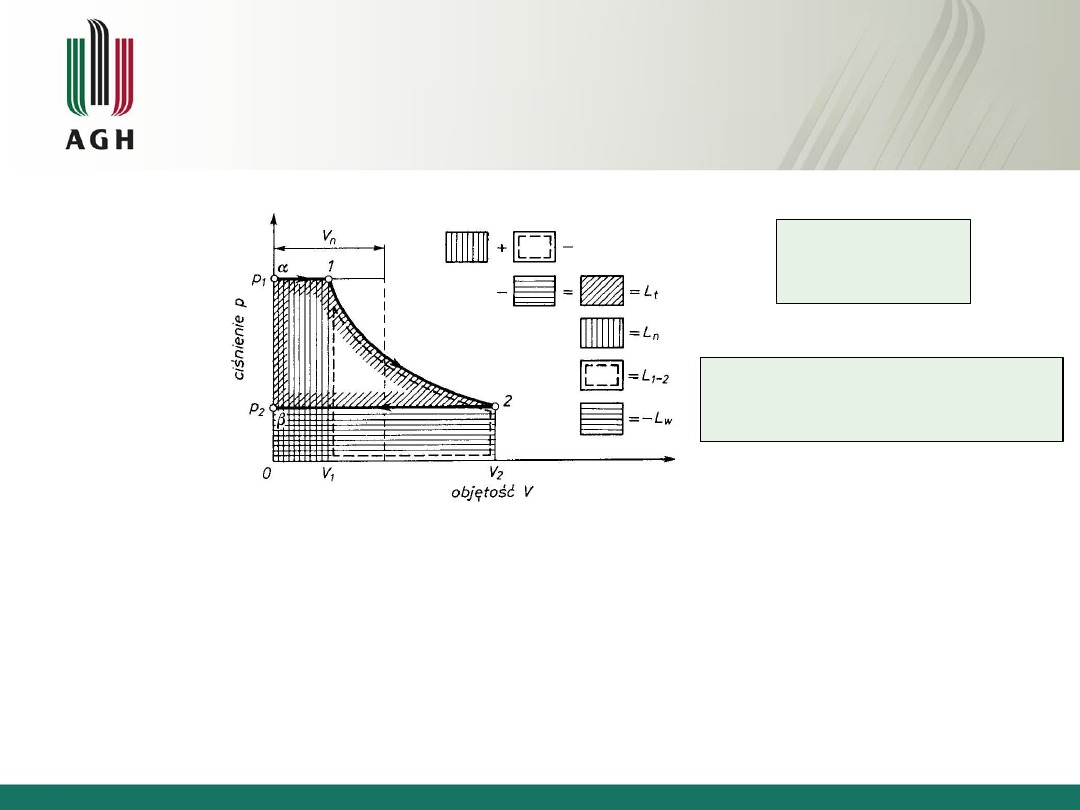
Praca
techniczna





2

1

2

1

p

p

V

Vdp

L

m

t













Vdp

dL

t





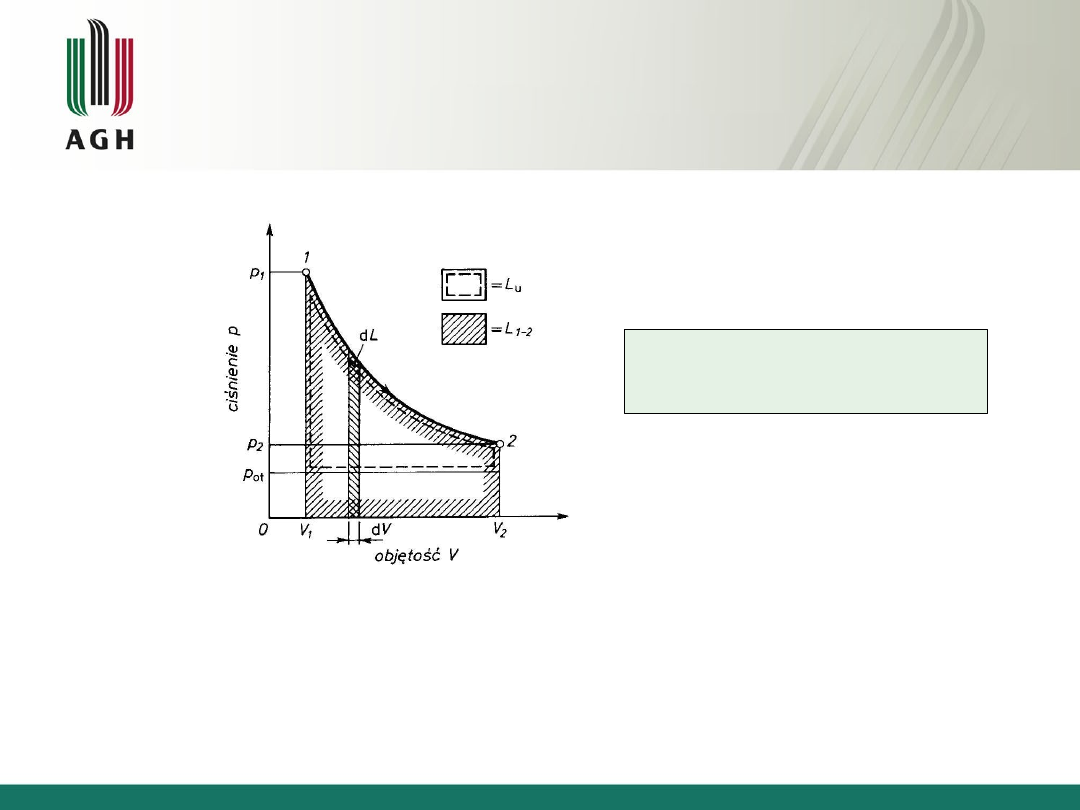
Praca
użyteczna





1

2

2

1

V

V

p

L

L

ot

u









