Correction Of Chromatic Abberration In Hybrid Objectives
03-02-24
str. 1/1
CORRECTION OF CHROMATIC ABERRATION
IN HYBRID OBJECTIVES
Marek Zając
Jerzy Nowak
Institute of Physics,
Wrocław University of Technology
Wyspiańskiego 27, PL 50-370 Wrocław, Poland
Email: zajac@if.pwr.wroc.pl
Key words:
Correction of aberrations
Hybrid lens
Chromatic aberration
ABSTRACT
In this paper two three-element's hybrid objectives are presented; in one of which one of
the lenses is made from fluorite, in the other - from special glass. Both have corrected
chromatic aberration in the wavelength range 0.435 µm<λ<0.852 µm. For both objectives
spherochromatic aberration is calculated and maximum aperture angle estimated. The imaging
quality obtained is compared to that of typical apochromatic objectives: refractive and hybrid
ones built without use of special glasses.
Correction Of Chromatic Abberration In Hybrid Objectives
03-02-24
str. 2/2
I. INTRODUCTION
State of chromatic aberration correction serves usually as the initial criterion of the optical
system usefulness. The simplest correction of this aberration can be obtained in doublet built
of two lenses made of conventional glasses of different Abbe numbers. For more advanced -
apochromatic - correction at least one special glass has to be used. Practically useful
achromatic objective is designed as three-component's one. The objective with the best
corrected chromatic aberration is superachromate, free from chromatism in the whole range of
wavelengths between 0.365 µm and 1.014 µm. As it has been shown by Herzberger [1] such
correction can be obtained in triplet objective made of appropriately chosen glasses. The
easiest way to receive superachromate is to use fluorite for one of the lenses, however one can
find a triple of glasses suitable for this aim.
In modern optics diffractive elements (DOE) as well as hybrid i.e. diffractive-refractive
lenses are used frequently. The diffractive structure has a form of concentric fringes deposited
on one of the lens surfaces. The geometry of fringes corresponds to the interference pattern
originated by two spherical waves of radii of curvature z
α
and z
β
and these values determine
the focusing power of diffractive structure [2]
−
=
Φ
β
α
λ
λ
z
z
D
1
1
0
(1)
where λ
0
is a wavelength for which the structure is designed and λ is the actual wavelength.
Dispersive properties of diffractive structure can be described by the parameters analogous
to Abbe number and partial dispersion defined as:
C
F
D
D
λ
−
λ
λ
=
ν
(2)
C
F
D
F
D
P
λ
λ
λ
λ
−
−
=
(3)
It is worth noticing that ν
D
differs substantially from Abbe numbers for all kinds of optical
materials, including special glasses, both in its value and its sign. The diffractive structure can
be used successfully as one of the components of an objective of corrected chromatic
aberration. In hybrid doublet we can have achromatic correction, however the secondary
spectrum is much greater than for classic glass achromates [3]. More advanced correction -
apochromatic - can be achieved in hybrid objective even without special glasses [3,4]
In this paper we investigate the possibility to compensate chromatic aberration in enlarged
wavelength range of a hybrid objective with special glasses as well as estimate a maximum
aperture for which spherochromatic aberration can be corrected.
II. CORECTION OF CHROMATIC ABERRATION IN TRIPLET
In order to obtain an apochromatic correction the following formulae should be fulfilled
0
3
3
2
2
1
1
=
Φ
+
Φ
+
Φ
ν
ν
ν
(4)
0
,
3
3
3
,
2
2
2
,
1
1
1
=
Φ
+
Φ
+
Φ
D
D
D
P
P
P
ν
ν
ν
(5)
1
3
2
1
=
Φ
+
Φ
+
Φ
(6)
where indices 1,2,3 denote particular elements composing hybrid triplet objective. The set
of equations (4-6) assure compensation of chromatic aberration for three wavelengths: λ
F
, λ
D
Correction Of Chromatic Abberration In Hybrid Objectives
03-02-24
str. 3/3
and λ
C
. Typically we assume, that diffractive structure is deposited on the first lens and
therefore for ν
1
, P
1,D
, Φ
1
the formulae (2), (3) and (1) have to be taken, while ν
2
P
2,D
, Φ
2
and
ν
3
P
3,D
, Φ
3
describe
The set of equations (4-6) has a non-zero solution if
0
1
1
1
3
2
1
,
3
,
2
,
1
≠
ν
ν
ν
D
D
D
P
P
P
(7)
The focusing powers of particular elements composing apochromatic triplet are given by:
(
)
3
2
1
3
1
1
ν
ν
ν
ν
ν
−
+
−
−
=
Φ
D
D
C
C
(8)
(
)
3
2
1
3
2
2
ν
ν
ν
ν
ν
−
+
−
=
Φ
D
C
(9)
(
)
(
)
3
2
1
3
2
3
1
ν
ν
ν
ν
ν
−
+
−
−
=
Φ
D
D
C
C
(10)
where
D
D
D
D
D
P
P
P
P
C
,
3
,
1
,
3
,
2
−
−
=
(11)
If the chromatic aberration is compensated for four wavelengths we have superachromatic
correction. To this aim the following condition has to be fulfilled [1]
0
1
1
1
2
,
3
2
,
2
2
,
1
1
,
3
1
,
2
1
,
1
=
λ
λ
λ
λ
λ
λ
P
P
P
P
P
P
(12)
The chromatic aberration equals zero for the wavelengths λ
1
, λ
F
, λ
C
and λ
2
and in the whole
range λ
1
<λ<λ
2
is practically compensated. For refractive triplet good correction can be
achieved in the wavelength range 0.365 µm<λ<1.014 µm. In many cases, in particular if the
objective is designed for visual instruments, such wide wavelength range seems to
unnecessary. Good chromatic correction for the range 0.435 µm<λ<0.852 µm can be obtained
using two refractive lens and one diffractive structure. In the following we assume that
diffractive structure is deposited on the first refractive surface.
III. CORRECTION OF SPHEROCHROMATIC ABERRATION
Two exemplary triplet objectives are designed according to the formulae derived in the
previous paragraph. Their construction data are presented in the Table 1 and denoted there as
No.3 and No.4 respectively. In the first of them fluorite is used.
For comparison two typical apochromatic lenses are taken and their data are also presented
in the Table 1. Typical glass apochromate [6] is denoted there as No.1 and hybrid
apochromate built without special glass [3] is denoted there as No.2.
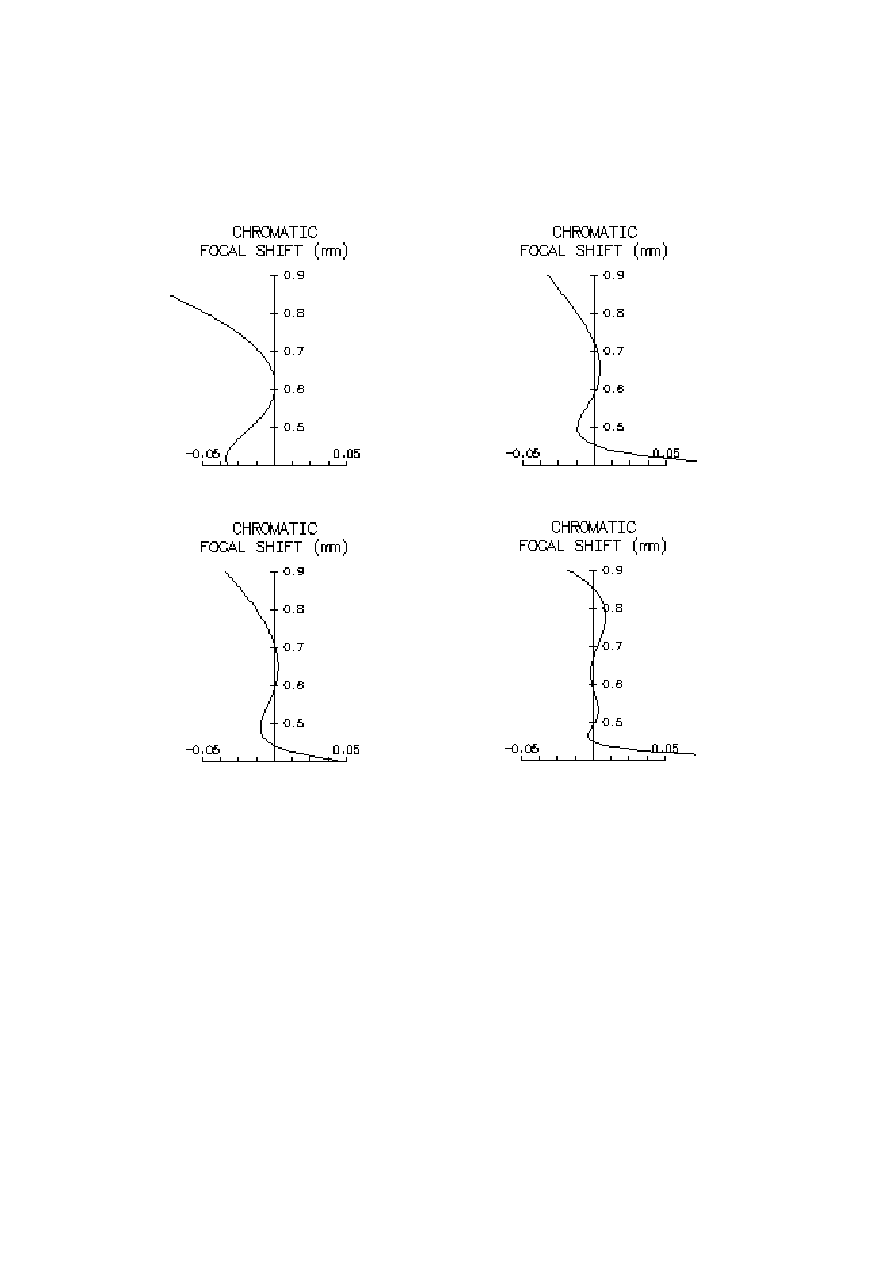
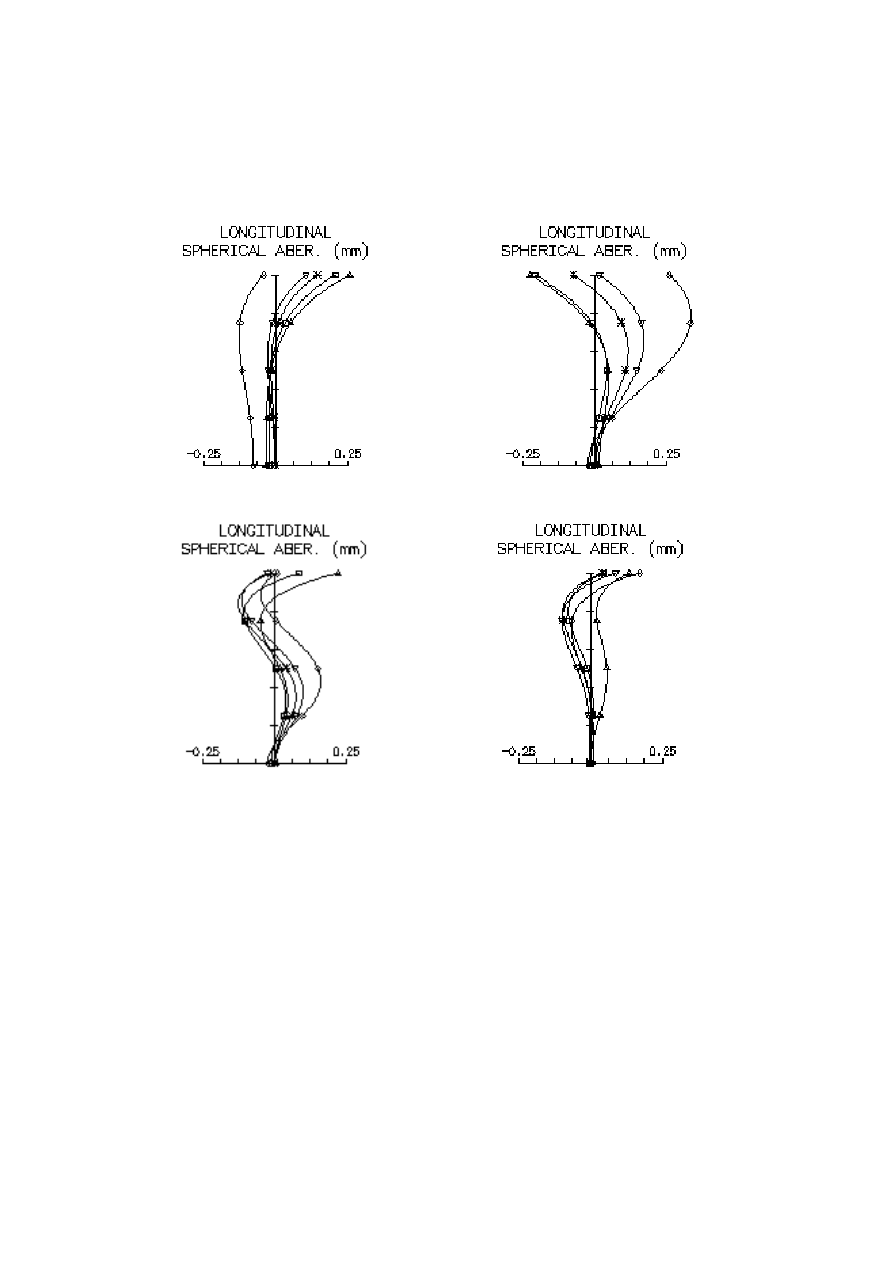
In the Figure 1 chromatic aberration curves for all four lenses are presented. It can be seen,
that correction of comparative objectives No.1 and No.2 is typically apochromatic, while the
wavelength range of chromatism correction for the lenses No. 3 and No. 4 is substantially
wider, as it was expected (especially for the lens with fluorite).
Sphero-chromatic aberration is presented in the Figure 2. In spite of the fact, that lenses
No.1 and No.2 were optimized only for three wavelengths
λ
F
,
λ
D
and
λ
C
on the graphs there
are also curves corresponding to
λ
g
= 0.436
µm and λ
s
= 0.852
µm. The F-number of
Correction Of Chromatic Abberration In Hybrid Objectives
03-02-24
str. 4/4
investigated lenses are F/5 for lenses No.1 and No.2, F/3 for lenses No.3 and No.4. This
choice follows from the analysis of spherochromatic aberration.
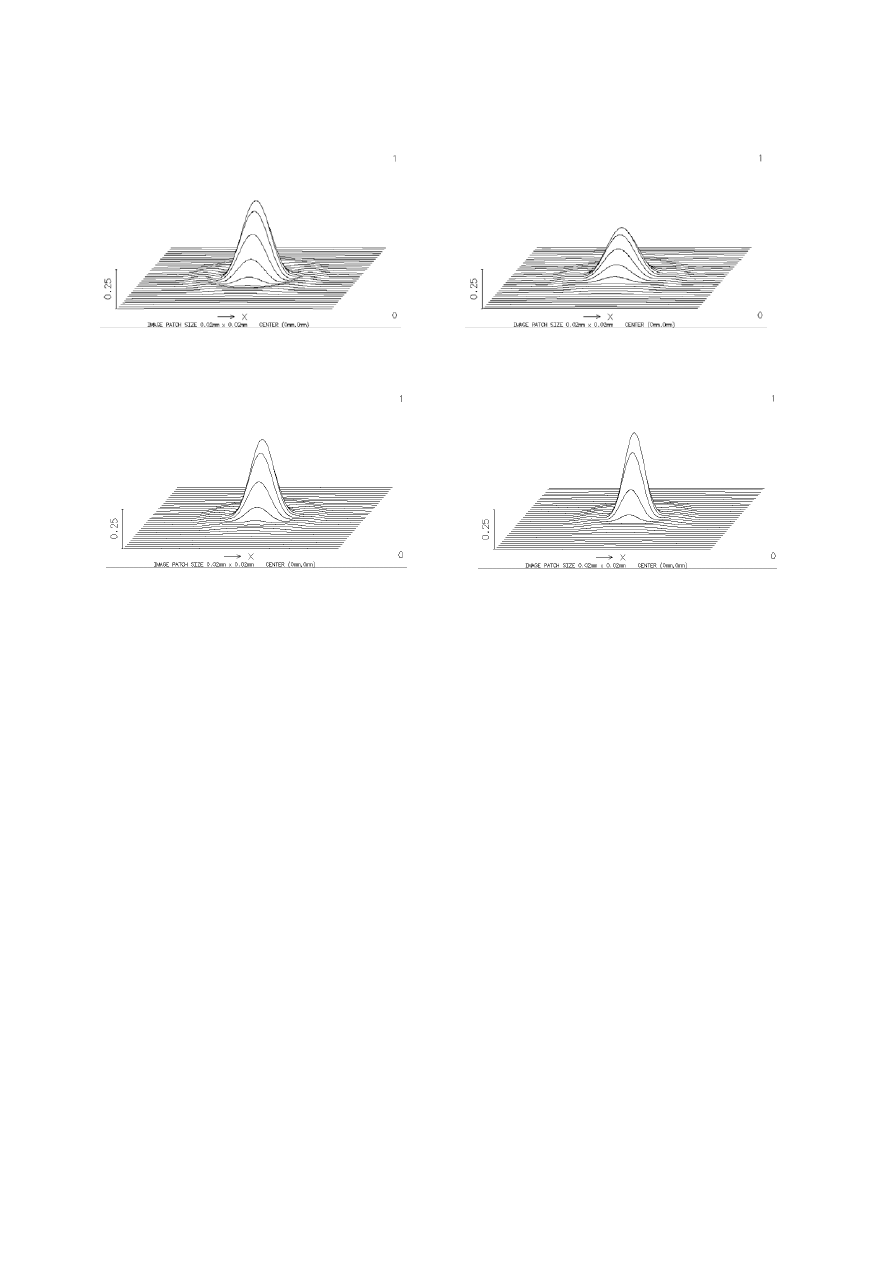
The estimation of the maximum acceptable aperture on the basis of spherochromatic
aberration seems to be not decisive. We verified it basing on the analysis of the size of
aberration spots assuming that that Marechal criterion has to be satisfied. The F-number for
which maximum intensity in the center of monochromatic aberration spot calculated in the
best focus plane is not smaller than o.8 are evaluated and given in the column 3 of the Table 2
(this column being denoted "F
M
". Since Marechal criterion is highly rigorous the lens aperture
can be slightly greater in practice. Therefore the following values: F/5 for the lenses No1 and
No2, F/4.5 for the lens No3 and F/4 for the lens No4 are adopted finally. For such objectives
polychromatic aberration spots are calculated in the best focus plane and presented in the
Figure 3. Some parameters characterizing these spots such as maximum intensity (I
max
) in the
spot center and diameter of the circle enclosing 80% of light energy (D
08
) are presented also
in the Table 2.
Analyzing the presented graphs and data we can conclude, that even apochromatic hybrid
objectives can be designed without use of special glasses the use of such glasses enables to
improve remarkably correction of sphero-chromatic aberration and obtain better chromatic
correction.
REFERENCES
1. Herzberger M., McClune N.R., Appl. Optics, vol. 2, 553, 1965,
2. Nowak J., Optica Aplicata, vol. 30, 213, 2000,
3. Nowak J., Masajada J., Opt. Applicata vol. 30, 271, 2000,
4. Smith W. J., Modern Optical Engineering, McGraw Hill Comp.,
5. "Zeemax 5e" Optical Design Program ver. 4.0.0, Focus Software Inc.,
Correction Of Chromatic Abberration In Hybrid Objectives
03-02-24
str. 5/5
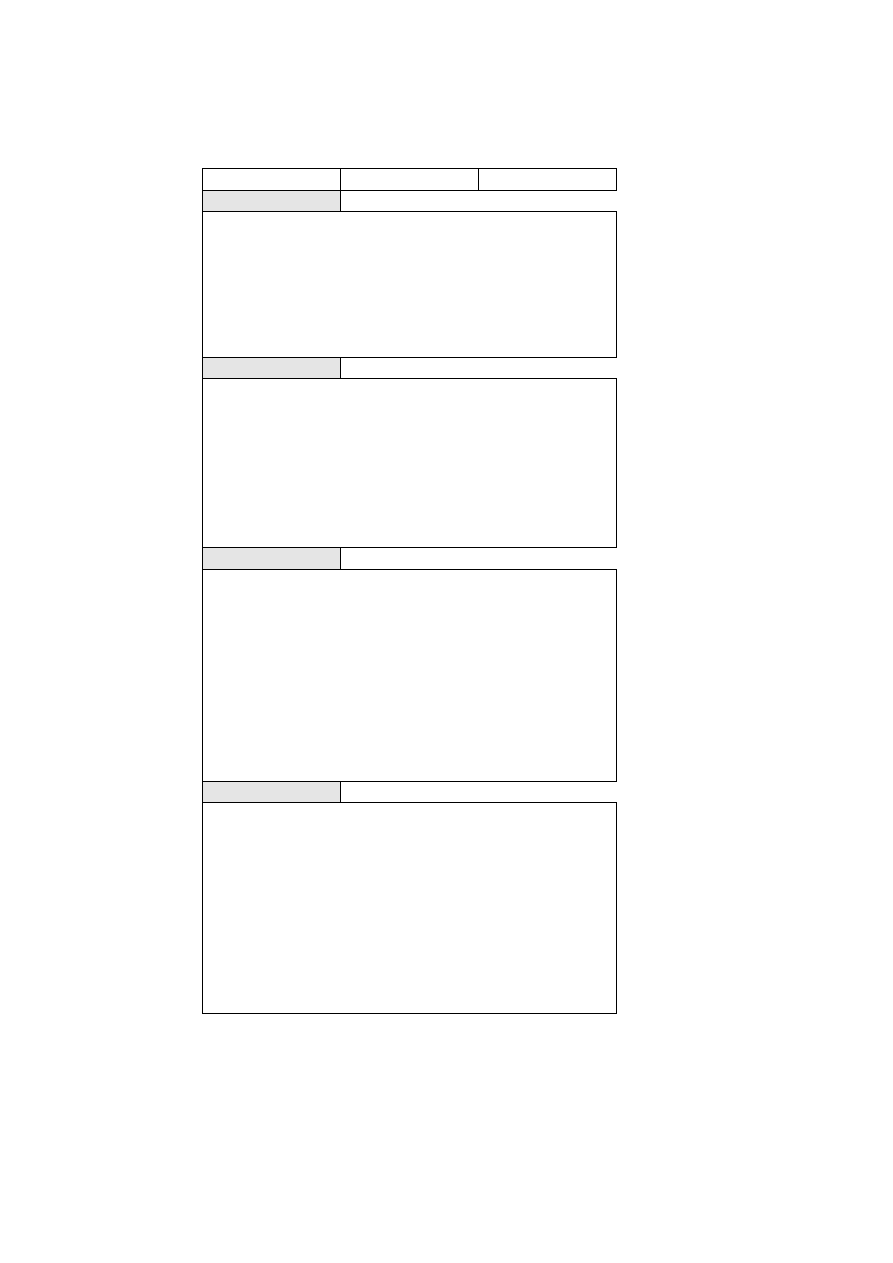
TABLE 1
Construction data of four investigated objectives
R [mm]
d [mm]
Glass/DOE
Lens No.1
63.434
2.0
F2
-35.212
2.0
KzFSN5
28.5395
2.0
FK51
-68.4290
Lens No.2
45.395
DOE
z
α
= -13.5000
z
β
= -13.4745
45.395
3.0
BK3
83.100
1.0
SF5
723.04
Lens No.3
40.00
DOE
z
α
= -12.0000
z
β
= -11.9919
40.00
7.0
FK52
-52.00
0.2
air
-51.45
1.0
BaF9
∞
Lens No.4
42.483
DOE
z
α
= -19.0000
z
β
= -18.9784
42.483
5.5
Fluorite
-125.0
0.8
air
-76.50
1.0
SF5
-150.8675
Correction Of Chromatic Abberration In Hybrid Objectives
03-02-24
str. 6/6
Table 2
Selected parameters describing imaging quality of four investigated objectives
Lens
F
M
final
F-number
I
max, mono
I
max, poli
D
08,poli
[mm]
No.1
F/4.75
F/5
0.90
0.64
0.016
No.2
F/4.85
F/5
0.88
0.42
0.028
No.3
F/4.35
F/4.5
0.86
0.66
0.013
No.4
F/3.88
F/4
0.84
0.72
0.011
Correction Of Chromatic Abberration In Hybrid Objectives
03-02-24
str. 7/7
a) b)
c) d)
Fig. 1 Chromatic aberration of four investigated objectives:
a) No.1, b) No.2, c) No.3, d) No4.
Correction Of Chromatic Abberration In Hybrid Objectives
03-02-24
str. 8/8
a) b)
c) d)
Fig. 2 Sphero-chromatic aberration of four investigated objectives:
b) No.1, F/5, b) No.2. F/5, c) No.3, F/3, d) No4, F/3.
Correction Of Chromatic Abberration In Hybrid Objectives
03-02-24
str. 9/9
a) b)
c) d)
Fig. 3 Polichromatic aberration spots in best focus plane for four investigated objectives:
c) No.1, F/5, b) No.2. F/5, c) No.3, F/4.5, d) No4, F/4.