Algorytmy i struktury danych

Lista, stos, kolejka

Struktury danych (1)

Struktura danych

– zbiór elementów. Każdy element składa

się z jednego lub więcej części (słów maszynowych),
zwanych

polami

.

p1

p2

p3

p4

Przykład

elementu

struktury danych

Pole p1 jest

wskaźnikiem

(dowiązaniem)

Pola p2, p3, p4 – dowolnego typu

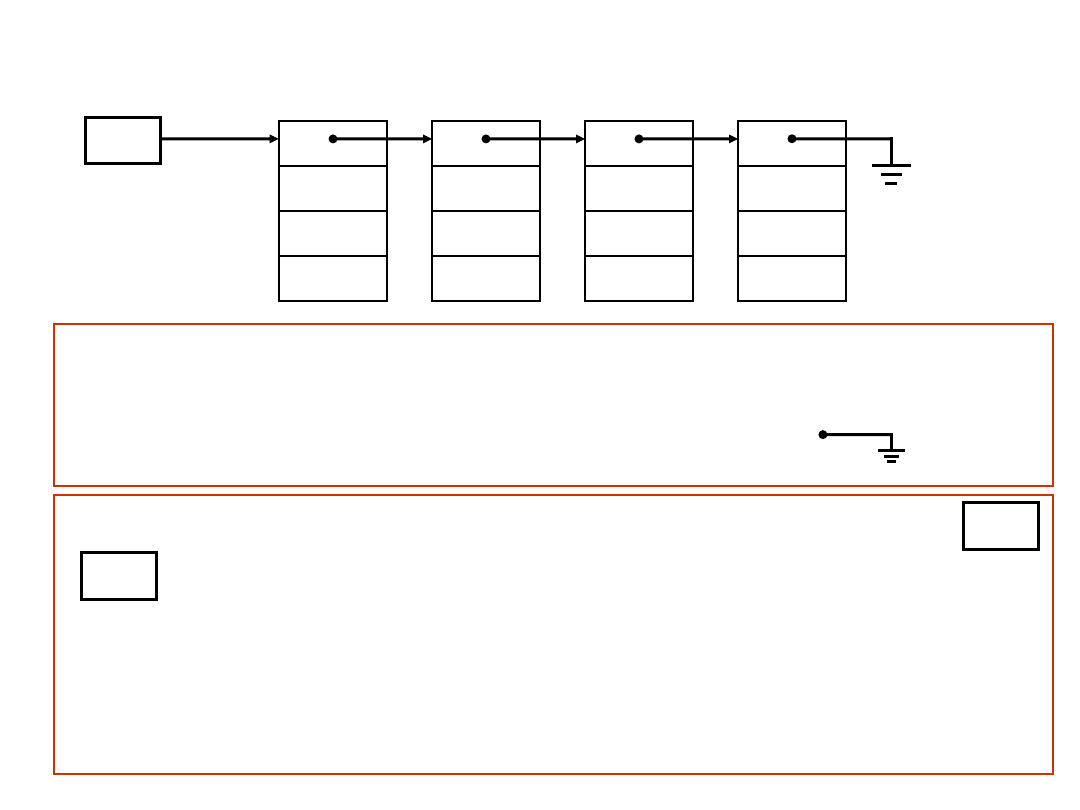
Wskaźnik (dowiązanie)

– podstawowy sposób reprezentowania

złożonych struktur danych.

Dowiązanie puste

– symbol



, symbol uziemienia

Na pierwszą wartość wskazuje wartość zapisana w zmiennej

to

zmienna wskaźnikowa

– zmienna, której wartościami

są wskaźniki (dowiązania).
Wszystkie

odwołania

do elementów struktury odbywają się

• bezpośrednio przez zmienne (lub stałe) wskaźnikowe
• pośrednio przez pola elementów struktury zawierające wskaźniki

Struktury danych (2)

p2

p3

p4

p2

p3

p4

p2

p3

p4

p2

p3

p4

TOP

TOP

TOP

Listy liniowe

Projekt reprezentacji

struktury danych:

• zdefiniowanie

informacji

(danych), które będą przechowywane

• zdefiniowanie

operacji

wykonywanych na danych

Wybór struktury danych zależy od powyższych czynników
i determinuje funkcjonalność struktury.

Lista liniowa

–ciąg n



0 elementów X[1], X[2], .., X[n],

w którym względna pozycja elementu zdefiniowana jest w porządku
liniowym.
Dla n > 0 X[1] jest pierwszym elementem, X[n] ostatnim
i jeśli 1 < k < n, to k-ty element X[k] leży za elementem X[k-1]
i przed elementem X[k+1].

Listy

Podstawowe

operacje na liście

:

• dostęp do k-tego elementu listy. Cel: odczyt lub modyfikacja

zawartości pól elementu

• wstawianie nowego elementu przed lub po k-tym elemencie
• usuwanie k-tego elementu
• wyznaczenie liczby elementów listy
• znajdowanie elementu listy o zadanej wartości jednego z pól

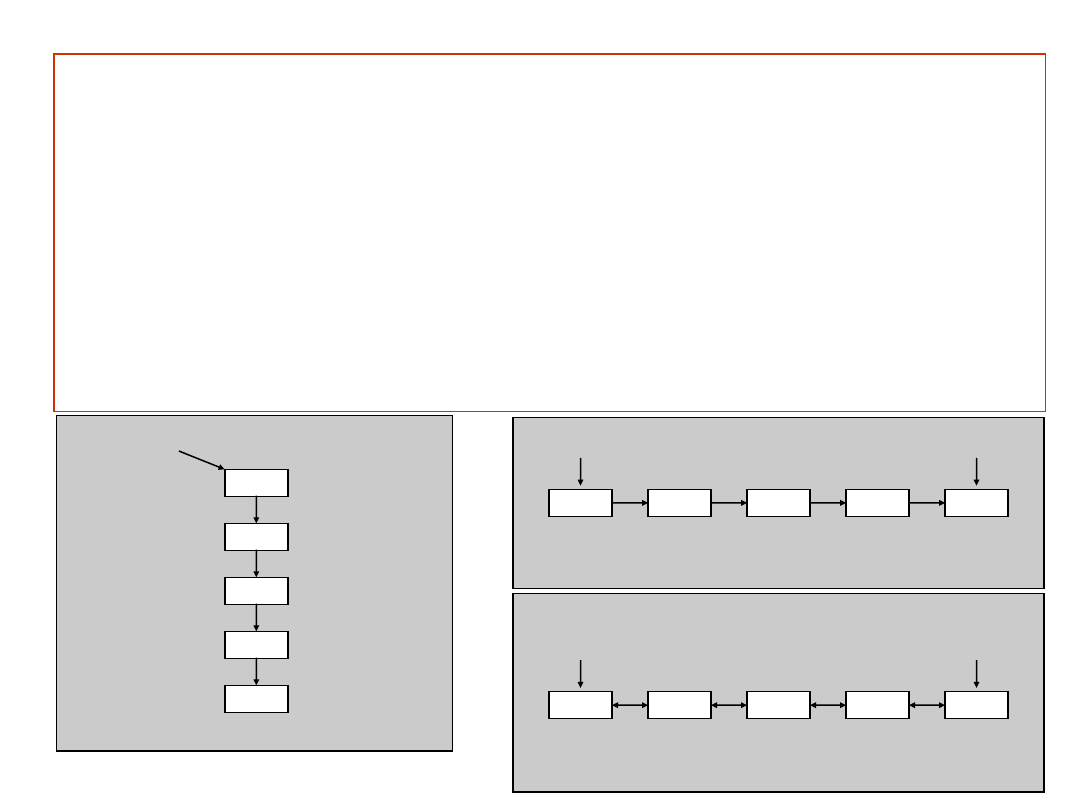
Stos

(ang. LIFO)– lista liniowa, dla której operacje wstawiania i

usuwania (oraz odczytu) elementu dotyczą tylko jednego końca
listy

Kolejka

(ang. FIFO)– lista liniowa, dla której operacje wstawiania

dotyczą jednego końca, a operacje usuwania (i odczytu) drugiego
końca

Kolejka dwustronna

– lista liniowa, dla której wszystkie operacje

wstawiania i usuwania (i odczytu) dotyczą dowolnego końca listy

Wstawianie
lub
zdejmowanie

wierzchołek

dno

Stos

Usuwanie

Wstawianie

pierwszy

ostatni

Kolejka

Wstawianie
lub usuwanie

lewy

prawy

Kolejka dwustronna

Wstawianie
lub usuwanie

Realizacja listy liniowej – tablice (1)

Metoda najprostsza: umieszczenie elementów listy liniowej w
kolejnych komórkach (lokacjach) pamięci:

Add(X[i+1]) = Add(X[i]) + c

Add – funkcja zwracająca adres początku elementu listy
c – liczba słów na jeden element listy

Jeśli L

0

– adres bazowy „hipotetycznego” elementu X[0], to

Add(X[i]) = L

0

+ ci

Najczęściej za pomocą tablicy realizowany jest

stos

.

Zmienna

T

nazywana jest

wskaźnikiem stosu

.

Operacje na stosie:

T=0

– stos pusty

T



T + 1; X[T]



Y

– wkładanie elementu Y na stos

Y



X[T]; T



T – 1

– zdejmowanie elementu ze stosu,

gdy stos jest niepusty

Realizacja listy liniowej – tablice (2)

Realizacja kolejki lub kolejki dwustronnej.
Przechowywane są dwa wskaźniki: F (front) i R (rear).
Operacje na kolejce dwustronnej:

F=R=0

– kolejka pusta

R



R + 1; X[R]



Y

– wkładanie elementu Y na koniec kolejki

F



F + 1; Y



X[F]

– usuwanie elementu z początku kolejki

Usprawnienie reprezentacji kolejki dwustronnej (lepsze
wykorzystanie pamięci, problem „przetaczającej się” kolejki):
X[1], .., X[M] – elementy ustawione w cykl, tak, że po X[M]
następuje element X[1]. Wtedy operacje mają postać:

jeśli R=M, to R



1, wpp R



R + 1; X[R]



Y

jeśli F=M, to F



1, wpp F



F + 1; Y



X[F]

Realizacja listy liniowej – tablice (3)

Problem przepełnienia (overflow, nadmiar elementów)
Problem niedomiaru (underflow, brak elementów)
Postać operacji dla stosu i kolejki dwustronnej:

X



Y (włóż na stos)

Y



X (usuń ze stosu)

X



Y (wstaw do kolejki)

`
Y



X (usuń z kolejki)

T



T+1;

jeśli T > M, to przepełnienie;
X[T]



Y;

jeśli T=0, to niedomiar;
Y



X[T];

T



T–1;

jeśli R=M, to R



1, wpp R



R+1;

jeśli F=R, to przepełnienie;
X[R]



Y;

jeśli F=R, to niedomiar;
jeśli F=M, to F



1, wpp F



F+1;

Y



X[F];

Realizacja listy liniowej – listy wskaźnikowe

Lista

p2

p3

p4

p2

p3

p4

p2

p3

p4

p2

p3

p4

Program wykorzystujący listę wskaźnikową musi pamiętać wskaźnik do
pierwszego elementu list

First

.

First

Porównanie realizacji listy liniowej z wykorzystaniem tablicy i wskaźników
• Struktura ze wskaźnikami wymaga dodatkowego pola na przechowywanie
wskaźnika.
• Operacja usunięcia elementu z listy jest prosta – wymaga jedynie zmiany
wskaźnika w odpowiednim elemencie. W przypadku sekwencyjnego przydziału
pamięci operacja ta wymaga przemieszczenia całego fragmentu listy do innych
lokacji pamięci.

•Wstawianie elementu w środek listy wskaźnikowej jest prostą operacją.
Wymaga zmiany wskaźników w dwóch elementach.

p2
p3
p4

p2
p3
p4

p2
p3
p4

p2
p3
p4

First

p2
p3
p4

p2
p3
p4

p2
p3
p4

p2
p3
p4

p2
p3
p4

First

p2
p3
p4

p2
p3
p4

Porównanie realizacji listy liniowej z wykorzystaniem tablicy i wskaźników
– cd.
• Odwołania do dowolnego elementu listy jest szybsze w przypadku tablic.
Dostęp do k-tego elementu listy w postaci tablicy jest stały, dla listy
wskaźnikowej wymaga k przejść po wskaźnikach.
• Operacja łączenia list wskaźnikowych jest prostsza niż list przy użyciu tablic.
• Lista wskaźnikowa umożliwia budowę skomplikowanych struktur, np. zmienna
liczba list o zmiennej długości: element listy „głównej” jest wskaźnikiem do listy
podrzędnej, lub elementy struktury mają wiele dowiązań i połączone są
równocześnie w różnych porządkach, odpowiadając różnym listom.
• Operacje przeglądania kolejnych elementów listy są szybsze dla list
sekwencyjnych.

• Do tworzenia listy wskaźnikowej niezbędny jest mechanizm przydzielania,
zwalniania, sprawdzania, czy można pamięć przydzielić, czyli

gospodarowania

pamięcią

.

•

Sterta

– zbiór wszystkich elementów przeznaczonych do dynamicznego

przydzielania.

info

link

Uwaga: Zakłada się, że element listy ma postać:

Stos

– realizacja poprzez listę wskaźnikową.

Zmienna wskaźnikowa T – wskazuje na wierzchołek stosu.

T=



– stos pusty

Włożenie informacji Y na stos T (wykorzystanie dodatkowej
zmiennej wskaźnikowej P):

P



new (element);

info(P)



Y;

link(P)



T;

T



P;

Przypisanie informacji do Y z wierzchołka stosu i zdjęcie ze stosu tej informacji:

jeśli

T =



to niedomiar;

wpp{

P



T;

T



link(P);

Y



info(P);

delete(P);

}

T

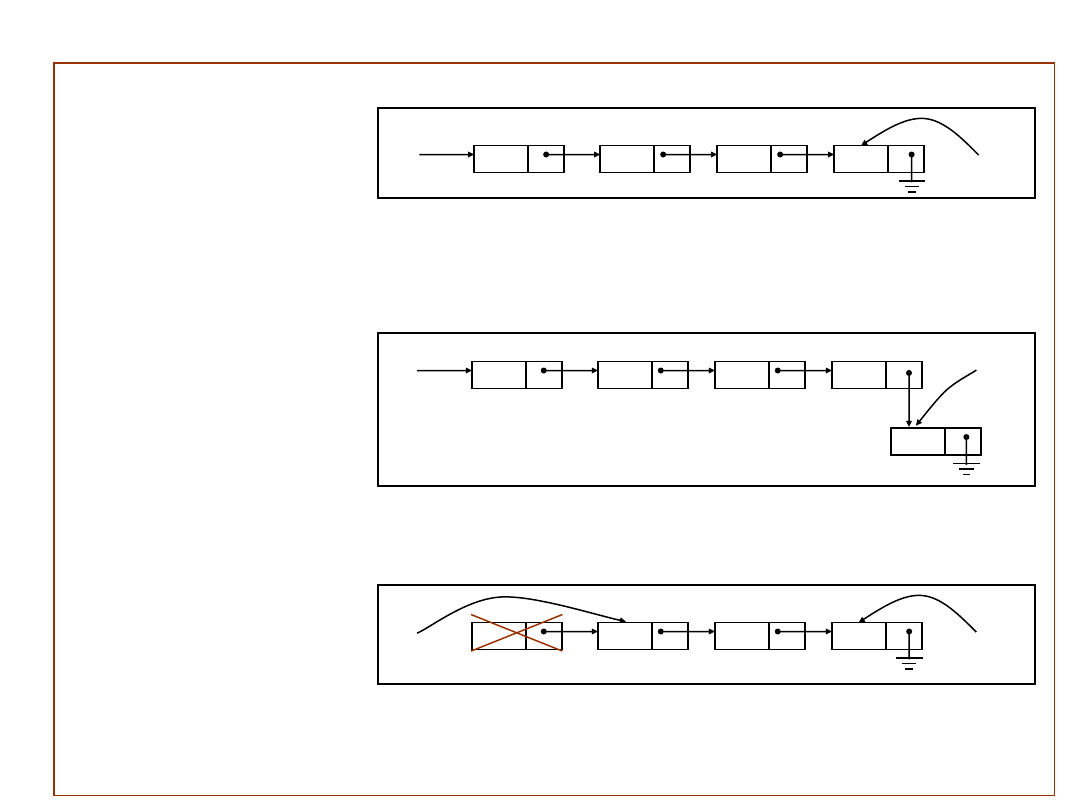
Kolejka

– realizacja poprzez listę wskaźnikową.

Kolejka pusta:

F=



i R=Add(F);

Operacja wstawiania nowego elementu do kolejki:

P



new(element);

info(P)



Y;

link(P)

 

;

link(R)



P;

R



P;

Operacja usuwania elementu z kolejki:

jeśli F=



to niedomiar;

wpp{

P



F;

F



link(P);

Y



info(P);

delete(P);
jeśli F=



to R=Add(F);}

F

R

F

R

P, nowy element

F

R

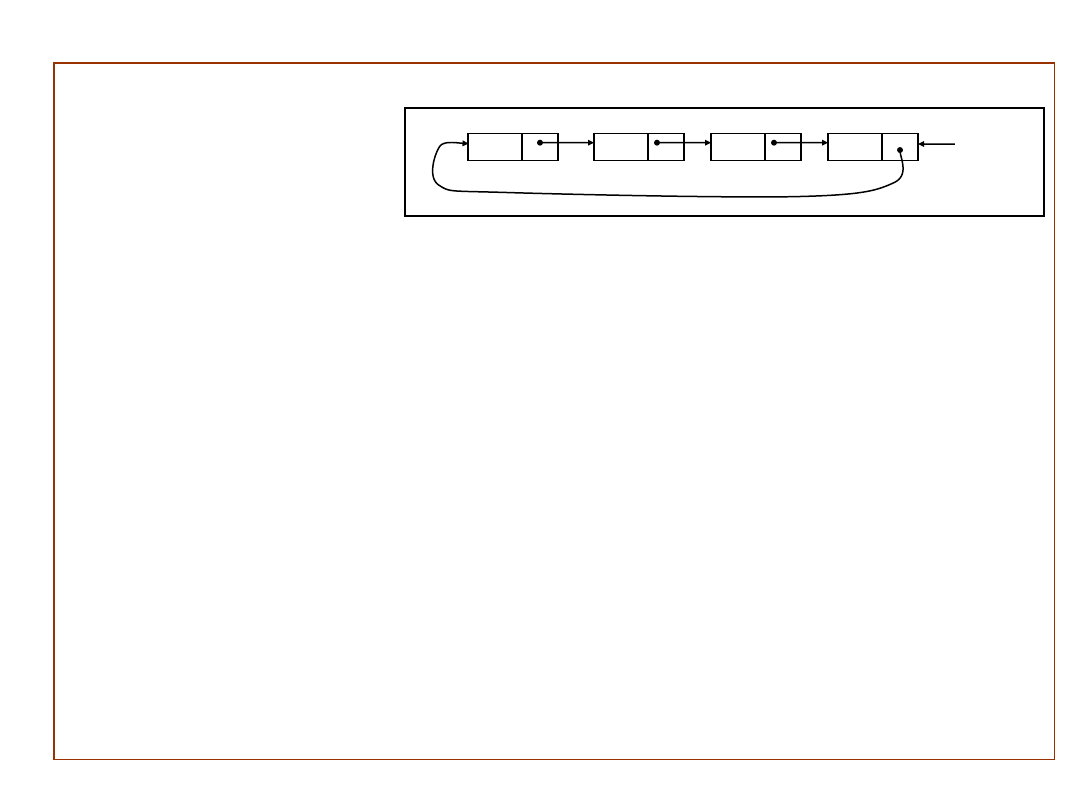
Lista cykliczna

– ostatni element listy wskazuje na pierwszy element.

Podstawowe operacje na listach cyklicznych:

PTR =



– lista pusta

Wstaw element Y z lewej strony:

P



new(element);

info(P)



Y;

jeśli PTR=



to PTR



link(P)



P;

wpp{

link(P)



link(PTR);

link(PTR)



P;

}

Wstaw element Y z prawej strony:

Wstaw Y z lewej strony;
PTR



P;

PTR

Usuń z listy lewy element:
jeśli

PTR=



to niedomiar

wpp{

P



link(PTR);

Y



info(P);

link(PTR)



link(P);

jeśli PTR=P to PTR

 

;

delete(P);

Dodawanie wielomianów z wykorzystaniem list cyklicznych

Problem: dodawanie wielomianów trzech zmiennych (x, y, z) o współczynnikach
całkowitych.

Element listy jest postaci:
i reprezentuje wyrażenie

coeff*x

A

y

B

z

C

Założenia:
1. znak słowa ABC jest zawsze równy + z wyjątkiem elementu specjalnego
reprezentującego koniec każdej listy, dla którego ABC= –1 i coeff=0.
2. elementy listy są zawsze ustawione w porządku malejącym względem pól ABC
(patrząc na listę zgodnie z kierunkiem dowiązań), przy czym element specjalny
wskazuje na element ABC o najwyższej wartości.

Przykład: x

6

– 6xy

5

+ 5y

6

link

C

B

A



coeff

0

0

6

+

+1

0

5

1

+

-6

0

6

0

+

+5

1

0

0

-

0

PTR

Algorytm: Dodawanie wielomianów.

Algorytm dodaje wielomiany: wielomian(P) i

wielomian(Q), reprezentowane przez listy. Wskaźniki do tych list to P i Q. Wynik
dodawania jest pamiętany w liście wskazywanej przez Q. Zmienne P i Q po wykonaniu
algorytmu mają z powrotem wartości początkowe. Zmienne Q

1

i Q

2

są wskaźnikowymi

zmiennymi pomocniczymi.

K1. Inicjalizowanie.

Podstaw P



link(P); Q

1



Q; Q



link(Q); Zmienne P i Q wskazują

na pierwsze wyrazy wielomianów.

K2. Porównanie ABC(P) i ABC(Q).

Jeśli ABC(P) < ABC(Q) {

Q

1



Q; Q



link(Q); powtórz krok K2}

Wpp{

Jeśli ABC(P) = ABC(Q) to krok K3;
Wpp krok K5; }

K3. Dodawanie współczynników.

Jeśli ABC(P) < 0 to STOP (zatrzymanie algorytmu);
Wpp{

coeff(Q)



coeff(Q) + coeff(P);

Jeśli coeff(Q)=0 to krok K4;
Wpp{

P



link(P); Q

1



Q; Q



link(Q); krok K2; }

K4. Usuwanie wyrazu zerowego.

Q2



Q; link(Q

1

)



Q



link(Q); delete(Q2);

P



link(P); krok K2;

K5. Wstawianie nowego wyrazu.

new(Q

2

); coeff(Q

2

)



coeff(P); ABC(Q

2

)



ABC(P); link(Q

2

)



Q;

link(Q

1

)



Q

2

; Q

1



Q

2

; P



link(P); krok K2.

Przykład: wywołanie algorytmu dodawania wielomianów dla wielomianów
x+y+z oraz x

2

–2y – z.

Algorytm: Mnożenie wielomianów.

Algorytm zastępuje wielomian(Q) wielomianem

postaci: wielomian(Q) + wielomian(M)*wielomian(P).

K1. Następny mnożnik.

Podstaw M



link(M). Jeśli ABC(M) < 0 to STOP.

Q

1



Q; Q



link(Q); Zmienne P i Q wskazują na pierwsze wyrazy wielomianów.

K2. Cykl mnożenia.

Wykonaj algorytm dodawania wielomianów, ale
1. każde wystąpienie ABC(P) w opisie algorytmu dodawania zamień na:
Jeśli ABC(P)<0 to –1;
Wpp ABC(P)+ABC(M)
2. Każde wystąpienie coeff(P) zamień na:
coeff(P)*coeff(M)
Wykonaj krok K1 algorytmu mnożenia wielomianów.