
Prędkości
Kosmiczne
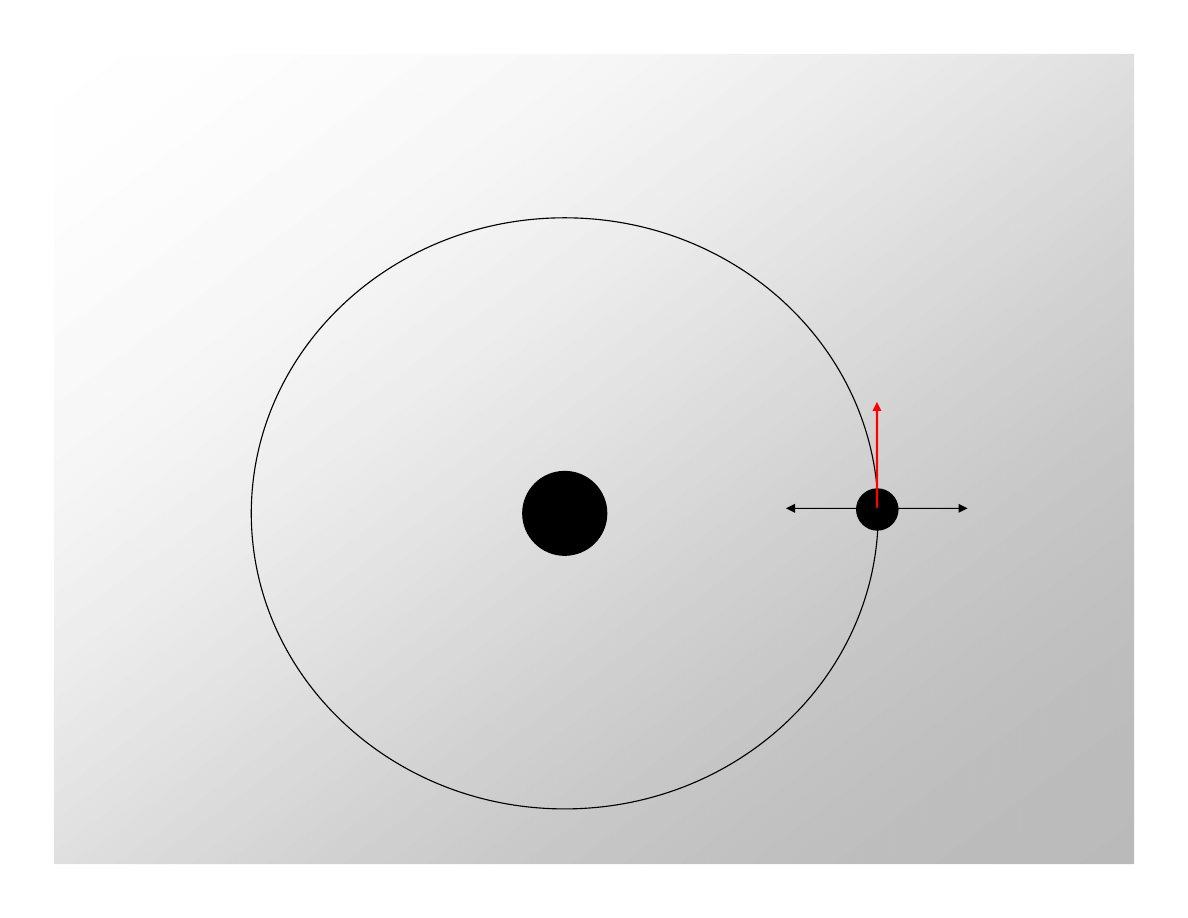
Pierwsza prędkość kosmiczna
Z
F
g
F
o
m
v
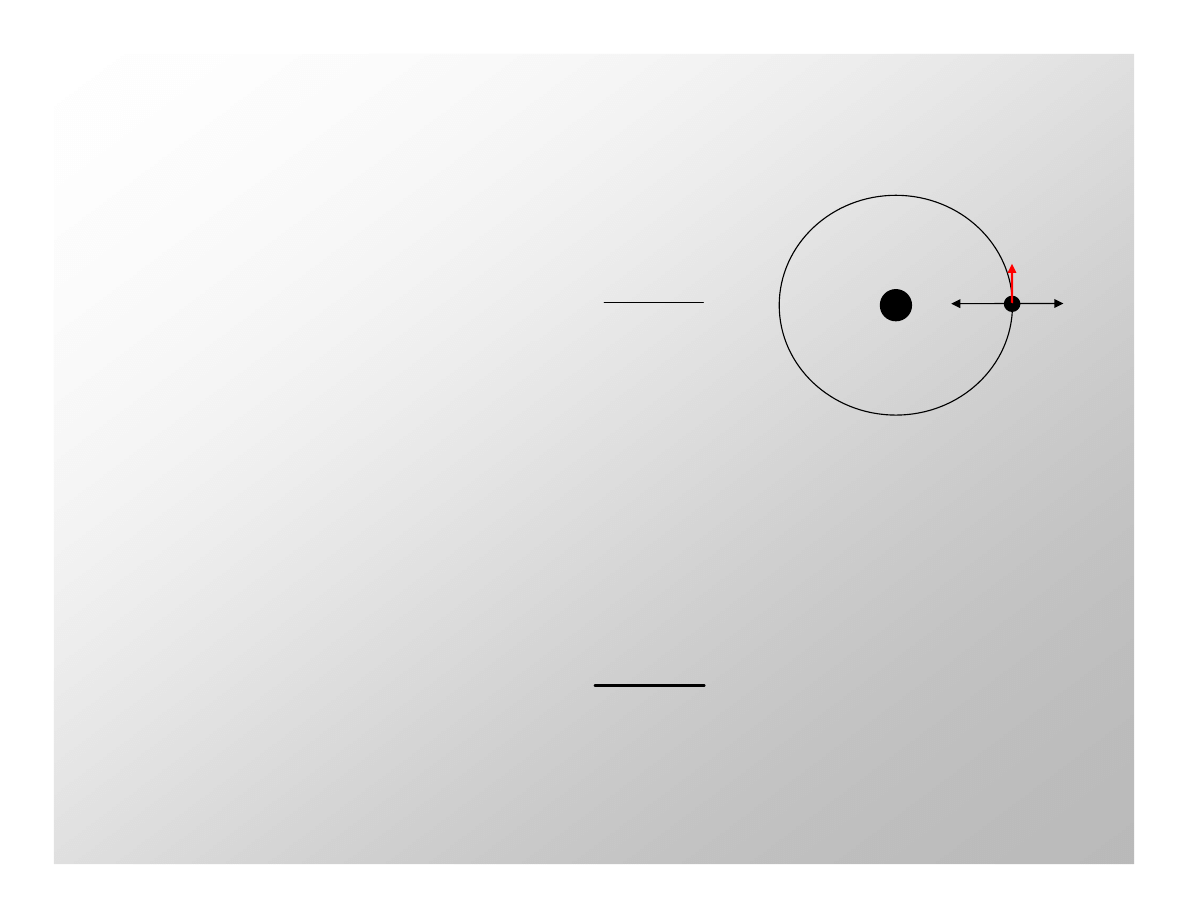
Pierwsza prędkość kosmiczna
2
r
M
G
m
F
g
⋅
=
siła oddziaływania grawitacyjnego wynosi
gdzie:
m – masa obiektu
G – stała grawitacyjna (6,672*10
-11
Nm
2
kg
-2
)
M – masa Ziemi (5,975*10
24
kg)
r – odległość od środka Ziemi
R
z
– promień Ziemi (6,378*10
6
m)
lub
2
r
m
F
g
µ
⋅
=
gdzie:
µ = G·M = 3,98652*10
14
Nm
2
kg
-1
F
g
F
o
v
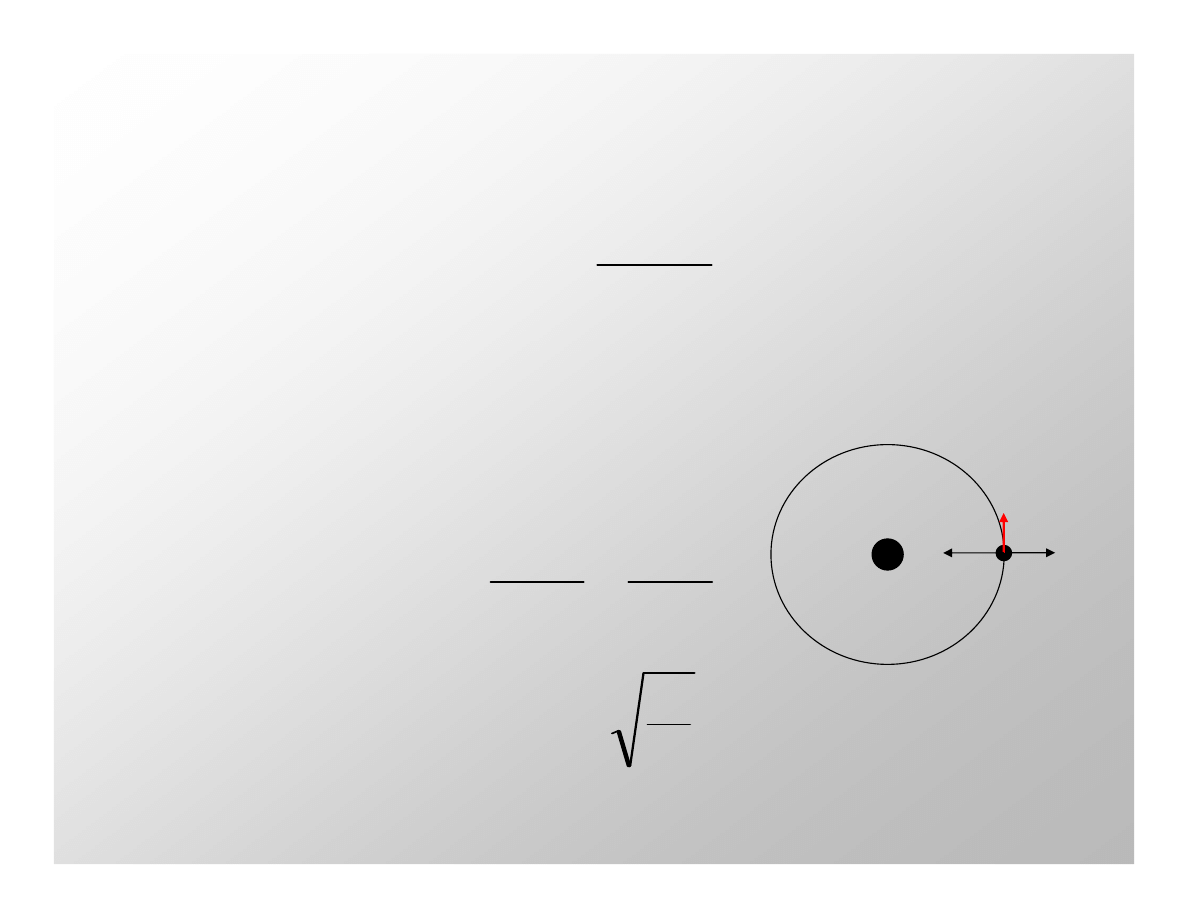
siła odśrodkowa w ruchu satelity po orbicie kołowej wynosi:
r
v
m
F
I
o
2
⋅
=
g
o
F
F
=
ponieważ satelita jest w równowadze (nie spada na Ziemię):
czyli:
2
2
r
m
r
v
m
I
µ
⋅
=
⋅
skąd:
r
v
I
µ
=
F
g
F
o
v
dla r = R
z
(promień Ziemi):
z
I
R
v
µ
=
po podstawieniu:
7906
10
6378
10
98652
,
3
3
14
=
⋅
⋅
=
I
v
m/s
9
,
7
≈
I
v
km/s
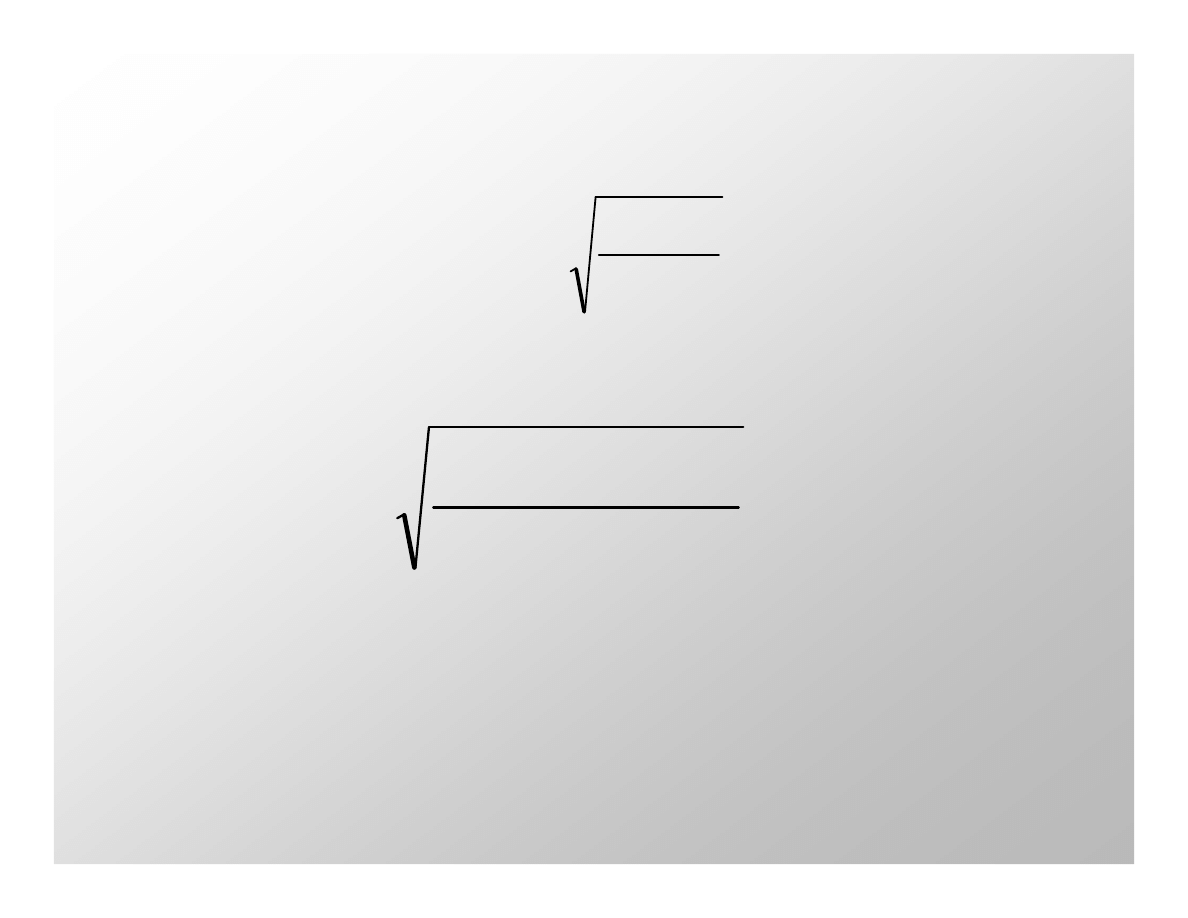
dla obiektu na wysokości h = 200 km nad powierzchnią Ziemi:
h
R
v
z
I
+
=
µ
po podstawieniu:
7785
10
6578
10
98652
,
3
3
14
=
⋅
⋅
=
I
v
m/s
8
,
7
≈
I
v
km/s

energia, którą trzeba dostarczyć satelicie aby wynieść go na zadaną
orbitę:
∫
=
∆
orbity
z
R
R
dr
r
m
E
2
µ
−
=
∆
orbity
z
R
R
m
E
1
1
µ
po scałkowaniu:
dla orbity znajdującej się na wysokości h = 200 km i masy 1 kg:
6
6
6
14
10
882
,
1
10
578
,
6
1
10
378
,
6
1
10
987
,
3
1
⋅
=
⋅
−
⋅
⋅
⋅
=
∆E
J

dodatkowa prędkość o jaką musimy rozpędzić satelitę (z równania na
energię kinetyczną):
E
v
∆
=
∆
2
1940
10
882
,
1
2
6
=
⋅
⋅
=
∆v
m/s
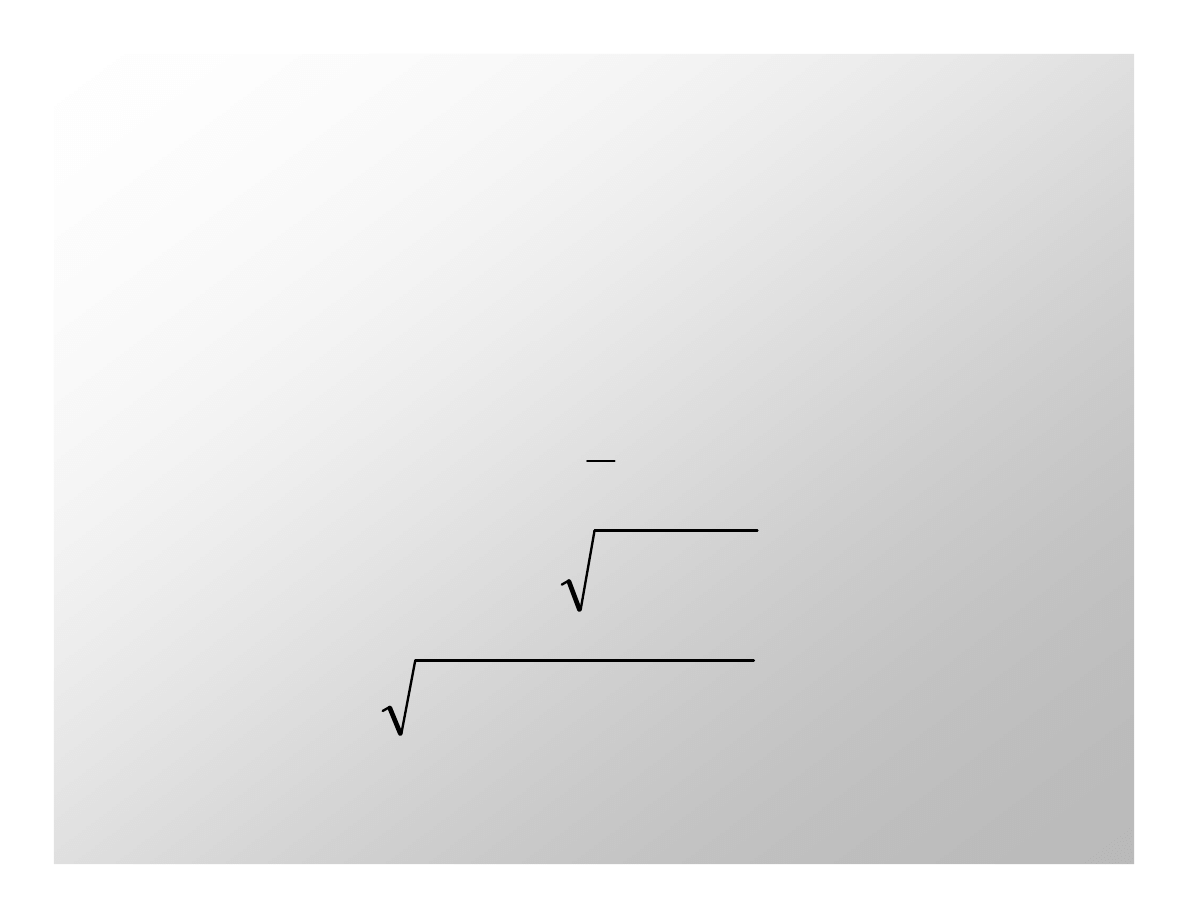
Jeśli całkowita energia satelity byłaby osiągalna równocześnie to ∆v dla satelity
(uwzględniając podniesienie satelity z powierzchni Ziemi na wysokość 200 km
oraz nadanie jej prędkości orbitalnej v = 7785 m/s) wynosiłaby:
k
c
E
E
E
km
+
∆
=
200
6
2
6
10
185
,
32
7785
2
1
10
882
,
1
200
⋅
=
+
⋅
=
km
c
E
stąd:
8024
10
185
,
32
2
6
=
⋅
⋅
=
∆v
m/s
km
c
E
v
200
2
=
∆
J

[J]
∆
v [m/s]
[J]
[m/s]
[km]
11089
8737
4116
1950
0
62,0*10
6
61,48*10
6
1020
384 000
5
50,3*10
6
38,16*10
6
4934
10 000
4
35,5*10
6
8,47*10
6
7350
1000
3
32,2*10
6
1,90*10
6
7785
(2)
200
2
31,2*10
6
0
≈
7900
(1)
0
1
Całkowita
nadana
energia
Energia niezbędna do
wyniesienia 1kg na daną
wysokość
Prędkość
orbitalna
Wysokość
orbity nad
powierzchnią
Ziemi
Lp
(1) – Ze względu na opór atmosferyczny satelita nie może być umieszczony
na tej orbicie
(2) – Satelita może przebywać na takiej orbicie przez okres paru dni-tygodni ze
względu na oddziaływanie szczątkowej atmosfery
-
1 000
2 000
3 000
4 000
5 000
6 000
7 000
8 000
9 000
0
50000
100000
150000
200000
250000
300000
350000
400000
450000
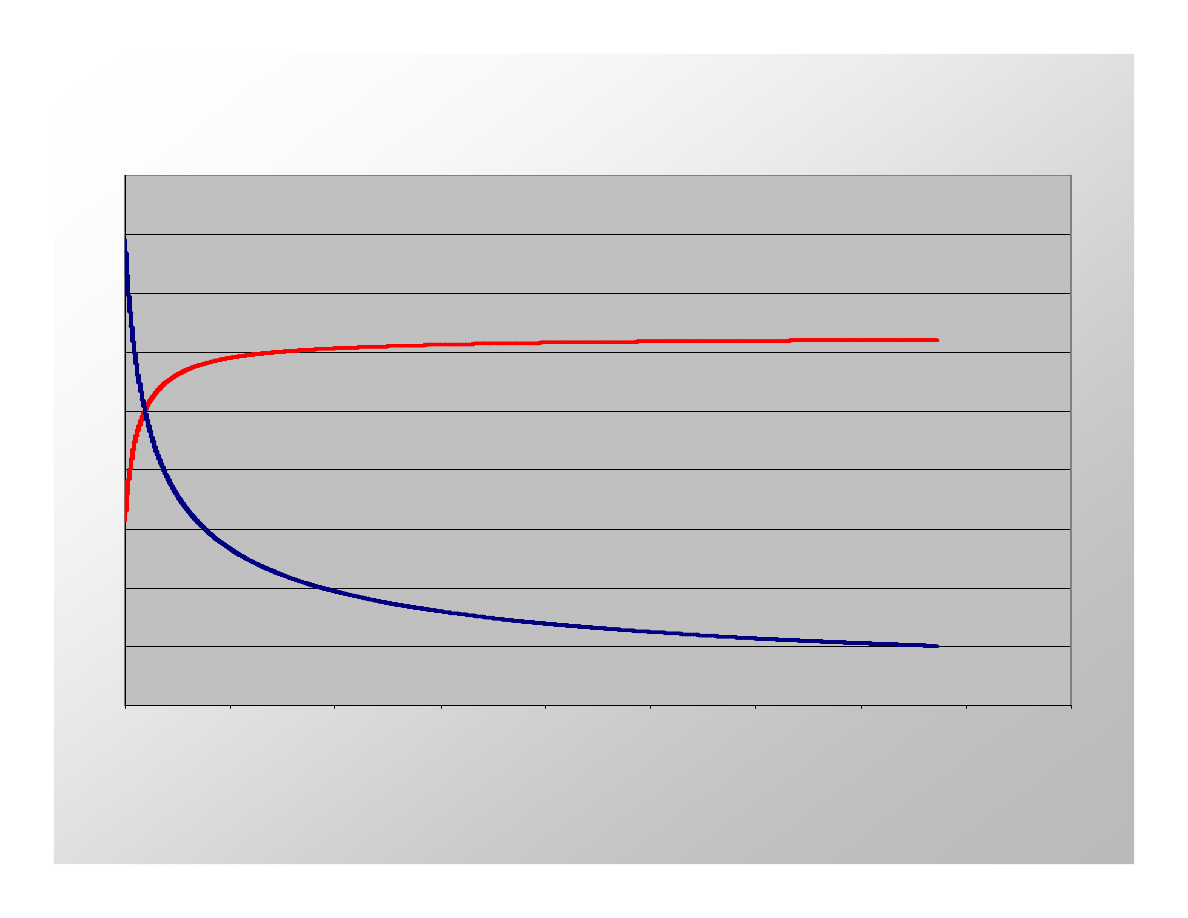
Wysokość [km]
Prędkość
satelity
Nadana energia
Prędkość satelity [m/s]
Nadana energia [10
4
J]

r
r
v
r
T
I
µ
π
π
2
2
=
=
µ
π
2
/
3
2
r
T
=
dla
h = 0 (r = 6378 km)
T = 5069 s
T ≈ 84,5 min = 1 godz. 24,5 min
h = 200 km
T = 5309 s = 1 godz. 28,5 min
h = 1 000 km
T = 1 godz. 45,1 min
h = 10 000 km
T = 5 godz. 47,5 min
h = 384 000 km
T = 27,4 dnia
Gwiazdowy miesiąc Księżycowy wynosi 27,3217 dnia
Okres obiegu satelity po orbicie kołowej:

Dla jakiej wysokości orbity okres obiegu będzie wynosił
jeden dzień gwiazdowy (23 godz. 56 min i 4,09 s) ?
r = 42 164 170 m
czyli około 35,786 km nad równikiem – orbita
Geostacjonarna (GEO); czyli około 35,8 tyś km
3
/
2
2
=
π
µ
T
r
µ
π
2
/
3
2
r
T
=
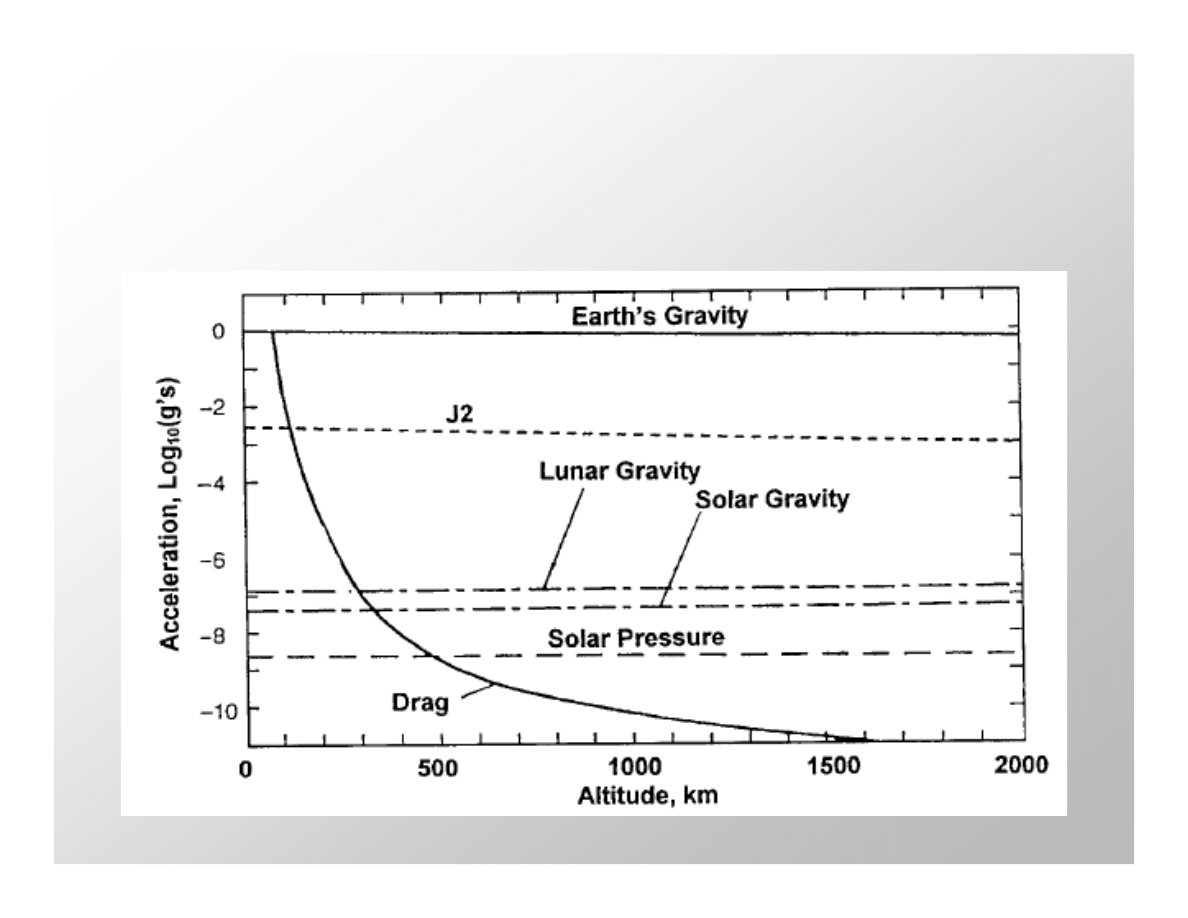
Wpływ różnych czynników na ruch
satelitów po orbicie Ziemi


Druga prędkość kosmiczna
całkowita energia niezbędna dla przesunięcia obiektu od powierzchni Ziemi w
nieskończoność wynosi:
∫
∞
−
=
z
R
c
dr
r
m
E
2
µ
z
c
R
m
E
µ
=
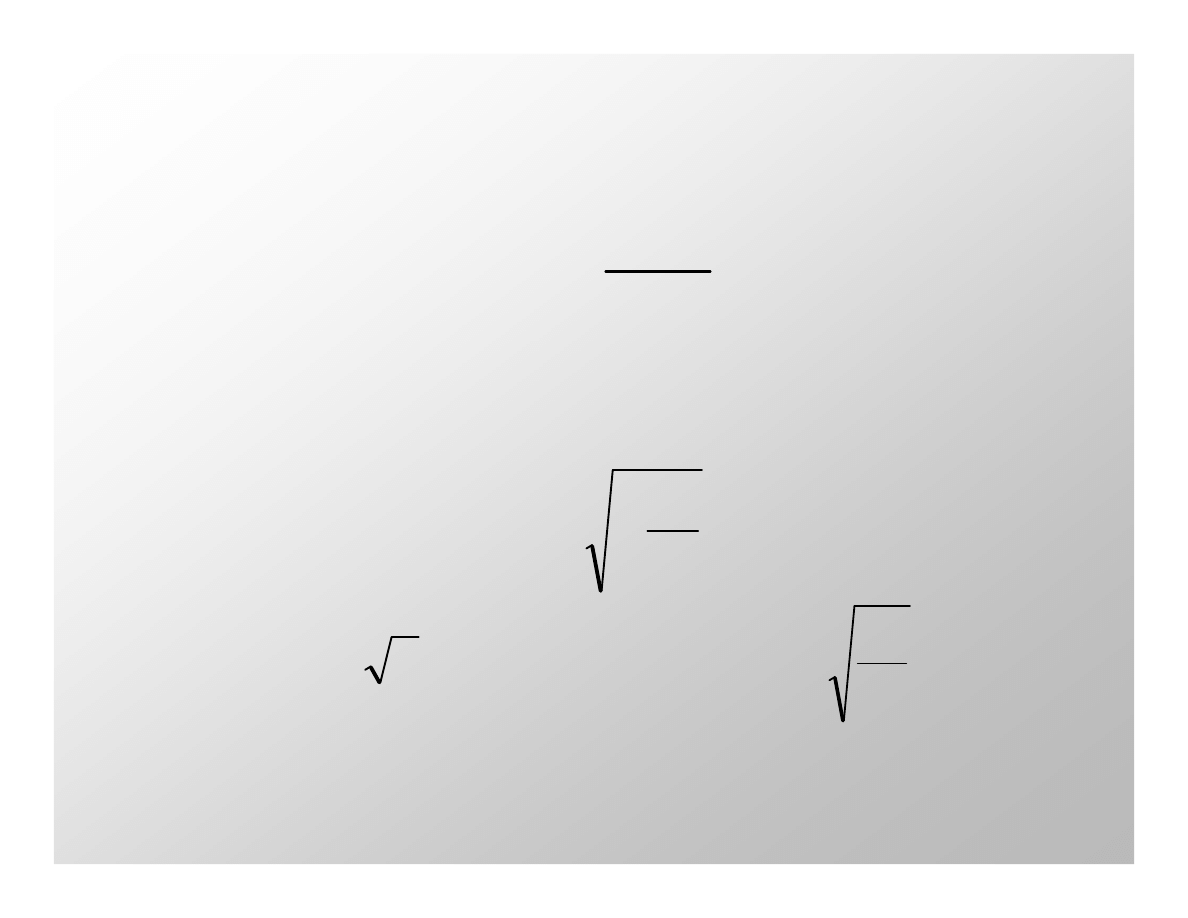
energia kinetyczna obiektu startującego z Ziemi z drugą prędkością kosmiczną
wynosi:
2
2
II
k
mv
E
=
c
k
E
E
=
z
II
R
v
µ
2
=
ponieważ:
to:
lub:
I
II
v
v
⋅
=
2
gdyż:
z
I
R
v
µ
=
= 11 180 m/s
lub:
II
v
II
v
≈ 11,2 km/s

62,5*10
6
11 181
62,50*10
6
0
∞
6
[J]
∆
v [m/s]
[J]
[m/s]
[km]
11 089
8 737
4 116
1 950
0
62,0*10
6
61,48*10
6
1020
384 000
5
50,3*10
6
38,16*10
6
4934
10 000
4
35,5*10
6
8,47*10
6
7350
1000
3
32,2*10
6
1,90*10
6
7785
(2)
200
2
31,2*10
6
0
≈
7900
(1)
0
1
Całkowita
nadana
energia
Energia niezbędna do
wyniesienia 1kg na daną
wysokość
Prędkość
orbitalna
Wysokość
orbity nad
powierzchnią
Ziemi
Lp
(1) – Ze względu na opór atmosferyczny satelita nie może być umieszczony
na tej orbicie
(2) – Satelita może przebywać na takiej orbicie przez okres paru dni-tygodni ze
względu na oddziaływanie szczątkowej atmosfery

Trzecia prędkość kosmiczna
prędkość ucieczki z Układu Słonecznego ciała znajdującego się w odległości
od Słońca równiej orbicie Ziemi wynosi:
≈ 42 200 m/s
III
v
ś
rednia prędkość Ziemi w ruchu po orbicie okołosłonecznej wynosi:
T
R
v
sz
Z
⋅
=
π
2
gdzie:
R
sz
– średnia odległość Ziemi od słońca (149,6*10
6
km)
T – okres obiegu słońca przez Ziemię, w sekundach (365,2564 dni)
=
⋅
⋅
⋅
⋅
=
3600
24
2564
,
365
10
6
,
149
2
9
π
Z
v
29 785 m/s
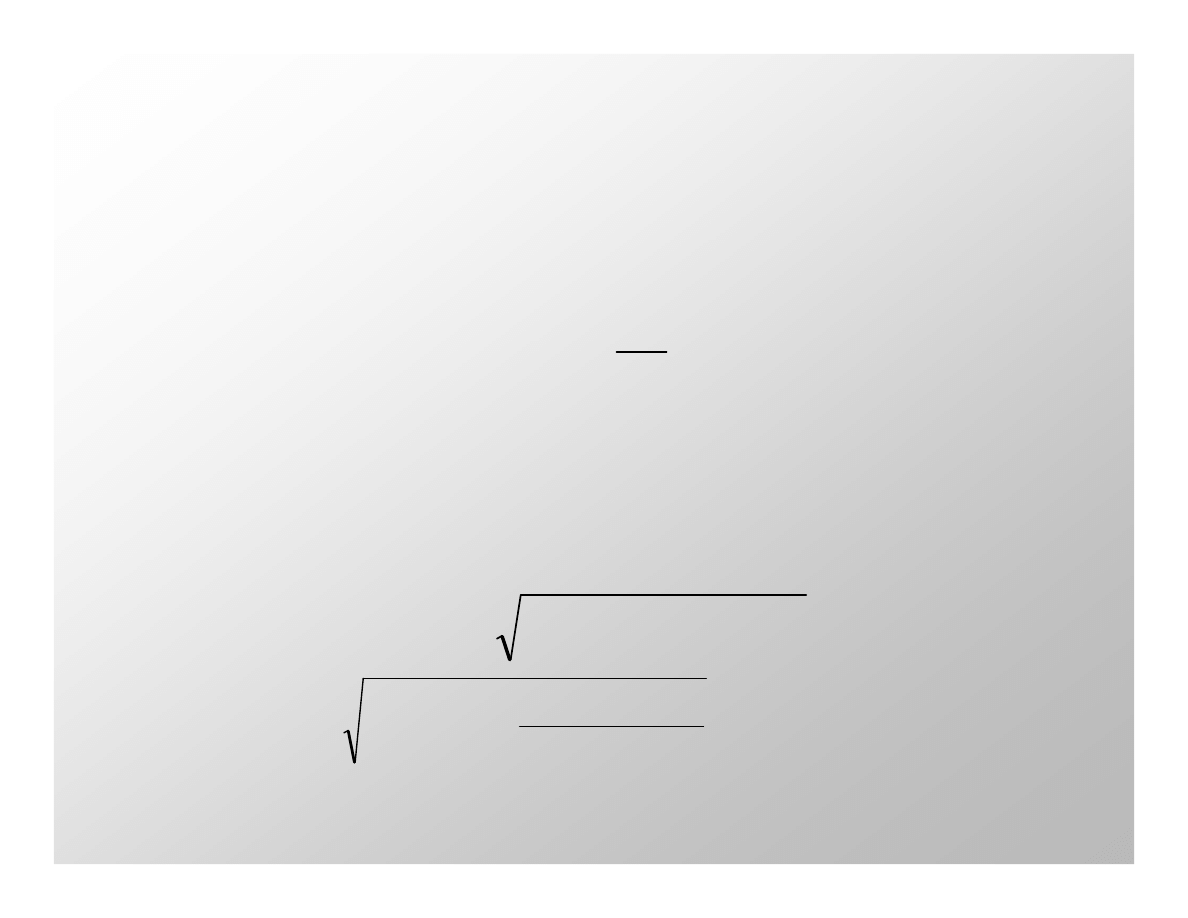
różnica prędkości wynosi wynosi:
=
−
z
III
v
v
12 415 m/s
energia niezbędna dla pokonania Ziemskiego pola grawitacyjnego równa się:
z
Z
R
E
µ
=
trzecia prędkość kosmiczna w przypadku startu z Ziemi w kierunku ruchu Ziemi
po orbicie okołosłonecznej wynosi:
(
)
z
z
III
III
E
v
v
v
Z
2
2
2
+
−
=
(
)
z
z
III
III
E
v
v
v
Z
2
2
+
−
=
=
⋅
⋅
+
=
3
14
2
10
6378
10
98652
,
3
2
12415
Z
III
v
16 707 m/s
≈
Z
III
v
16,7 km/s

prędkość niezbędna dla zapewnienia bezpośredniego
spadku na Słońce przy starcie z Ziemi.
ś
rednia prędkość ruchu Ziemi po orbicie okołosłonecznej wynosi:
=
Z
v
29 785 m/s
rakietę należy więc wystrzelić w kierunku przeciwnym z prędkością:
z
z
E
v
v
2
2
2
+
=
=
+
=
z
z
E
v
v
2
2
31 814 m/s
≈
v
31,8 km/s
Wyszukiwarka
Podobne podstrony:
Prędkość kosmiczna, Fizyka
Fizyka i astronomia fizyka pp k Nieznany
Fizyka i astronomia fizyka pr k Nieznany
PRĘDKOŚCI KOSMICZNE, NAUKA, WIEDZA
Fizyka i astronomia 6 id 176768 Nieznany
predkosci kosmiczne, Fizyka
Prędkości kosmiczne
Fizyka - II predkosc kosmiczna, szkola, Fizyka
praca w polu grawitacyjnym, predkosci kosmiczne
Fiz-pola grawitacyjne, Pierwsza prędkość kosmiczna jest to prędkość jaką należy nadać ciału wyżucone
Fizyka i astronomia 4 id 176764 Nieznany
27. Prędkości kosmiczne, Fizyka - Lekcje
Predkosci kosmiczne zadanie na fizyke
ASTRONAUTYKA STACJE KOSMICZNE
praca w polu grawitacyjnym, predkosci kosmiczne
Dodawanie predkosci id 138890 Nieznany
1 Zastosowanie parametru predko Nieznany (2)
08 Predkosc deformacjiid 7486 Nieznany (2)
więcej podobnych podstron