
POLITECHNIKA BIAŁOSTOCKA
WYDZIAŁ ELEKTRYCZNY
___________________________________________________________
Laboratorium Miernictwa Elektrycznego
Podstawowe zagadnienia metrologii
Instrukcja do
ć
wiczenia
Nr 11
Opracował dr in
ż
. R. Piotrowski
______________________________________________
Białystok 1998

Ć
wicz. Nr 11 Podstawowe zagadnienia metrologii
2
1. Wprowadzenie
1.1. Identyfikacja cech
ystematyzuj
ą
c wiedz
ę
dotycz
ą
c
ą
procesu pomiarowego stwierdzamy,
ż
e na
samym pocz
ą
tku tego procesu wyst
ę
puje identyfikacja cech.
Jest to odkrywanie i
ś
cisłe okre
ś
lanie cech ciał i zjawisk u
ż
ytecznych dla
człowieka z praktycznego i naukowego punktu widzenia.
Jak łatwo zauwa
ż
y
ć
, nie mierzymy w istocie przedmiotów (ogólnie ciał) ani
zjawisk fizycznych lecz poszczególne ich cechy. Na przykład zadanie zmierzenia
walca wykonanego z miedzi jest zadaniem w gruncie rzeczy nieokre
ś
lonym. Nie
unikniemy pytania, o pomiar jakiej cechy tego obiektu chodzi. Pomiarowi podlega
ć
mog
ą
bowiem takie u
ż
yteczne dla człowieka cechy tego obiektu jak: masa, długo
ś ć
,
ś
rednica, rezystancja, rezystywno
ś ć
, i jeszcze kilka innych bardziej wyrafinowanych
cech. O istnieniu wielu z nich nie wiedziano na przykład jeszcze sto lat temu.
Identyfikacja jest procesem ci
ą
głym, polegaj
ą
cym na odkrywaniu coraz to nowych,
po
ż
ytecznych dla człowieka cech otaczaj
ą
cej go przyrody.
Ś
cisłe okre
ś
lanie nowo odkrytej cechy polega na formułowaniu jej definicji,
która z jednej strony ujawnia jej zwi
ą
zek z innymi cechami, z drugiej za
ś
strony
stanowi przepis na jej pomiar. Na przykład taka cecha ciał jak rezystancja jest
zwi
ą
zana z napi
ę
ciem elektrycznym i nat
ę ż
eniem pr
ą
du znan
ą
zale
ż
no
ś
ci
ą
,
R
U
I
=
Zale
ż
no
ś ć
ta stanowi jednocze
ś
nie przepis na pomiar rezystancji, który brzmi:
„We
ź
napi
ę
cie przyło
ż
one do ko
ń
ców rozwa
ż
anego ciała stałego oraz nat
ę ż
enie
pr
ą
du, które to napi
ę
cie w nim wymusiło i podziel wspomniane wy
ż
ej wielko
ś
ci”
S

Ć
wicz. Nr 11 Podstawowe zagadnienia metrologii
3
Niestety, nie wszystkie wielko
ś
ci mierzalne mog
ą
mie
ć
ze wzgl
ę
dów
formalnych swoje definicje. Przyczyny tego stanu rzeczy zostan
ą
wyja
ś
nione w
dalszej cz
ę ś
ci wprowadzenia.
W
ś
ród cech, jakie dostrzegamy w ciałach i zjawiskach, nie wszystkie
podlegaj
ą
ś
cisłej ocenie, to znaczy nie wszystkim mo
ż
emy w racjonalny sposób
przypisa
ć
w wyniku pomiaru licz
ę
. Te cechy, którym umiemy przypisa
ć
liczb
ę
, czyli
jak powiadamy - odwzorowa
ć
liczb
ą
, nazywamy wielko
ś
ciami mierzalnymi,
wielko
ś
ciami
fizycznymi
lub
krótko
-
wielko
ś
ciami.
Do
zagadnienia
odwzorowywania cech liczbami jeszcze powrócimy.
Dla przykładu, masa, długo
ść
, rezystancja s
ą
cechami mierzalnymi, umiemy
bowiem w racjonalny sposób przypisywa
ć
tym cechom liczby, natomiast pi
ę
kno,
romantyzm, złowró
ż
ebno
ść
, nie s
ą
mierzalne, a wi
ę
c nie s
ą
one wielko
ś
ciami
mierzalnymi.
Proces identyfikacji zawiera kilka nieodzownych operacji:
•
Odkrycie interesuj
ą
cej człowieka cechy ciała lub zjawiska
•
Ś
cisłe okre
ś
lenie jej przez sformułowanie definicji
•
Nadanie jej nazwy słownej
•
Oznaczenie symbolem literowym
•
Powołanie do
ż
ycia jednostki miary
•
Nadanie nazwy jednostce
•
Oznaczenie jednostki symbolem literowym
W Tablicy 1 przedstawiono przykłady nazw i symboli kilku wielko
ś
ci
mierzalnych oraz odpowiadaj
ą
cych im jednostek miar.
Tablica 1
L.p.
Nazwa wielko
ś
ci
Symbol
wielko
ś
ci
Nazwa
jednostki
Symbol
jednostki
1
długo
ść
l
metr
m
2
masa
m
kilogram
kg
3
czas
t
sekunda
s
4
nat
ę ż
enie pr
ą
du elektrycznego
i
amper
A
5
rezystancja
R
om
Ω
6
pojemno
ść
elektryczna
C
farad
F
7
indukcja magnetyczna
B
tesla
T
8
indukcyjno
ść
własna
L
henr
H

Ć
wicz. Nr 11 Podstawowe zagadnienia metrologii
4
1.2. Jednostka miary
Jednostka miary jest to wielko
ść
mierzalna danego rodzaju, której umownie
przypisuje si
ę
liczb
ę
jeden, nadaje nazw
ę
i oznacza symbolem.
Wielko
ść
danego rodzaju to znaczy interesuj
ą
c
ą
nas mierzalna cecha
uciele
ś
niona w danym ciele lub zjawisku. Na przykład taka cecha ciała jak długo
ść
uciele
ś
niona jest w ka
ż
dym przedmiocie posiadaj
ą
cym prostoliniow
ą
kraw
ę
d
ź
, za
ś
masa w dowolnym w zasadzie ciele stałym lub ciekłym.
Jednostka miary jest elementarnym narz
ę
dziem pomiarowym, zatem
najbardziej odpowiedzialn
ą
cz
ęś
ci
ą
procesu jej ustalania, jest racjonalne obranie
postaci materialnej jednostki (ciała lub urz
ą
dzenia odtwarzaj
ą
cego zjawisko).
Przypisanie liczby jeden, podobnie jak nadanie jednostce nazwy słownej i symbolu
literowego ma ju
ż
tylko charakter formalny i dokonuje si
ę
w wyniku powszechnie
przyjmowanej umowy.
1.3. Pomiar
Pomiar jest do
ś
wiadczeniem fizycznym, w wyniku którego wielko
ś
ci
mierzalnej zostaje przyporz
ą
dkowana liczba, inaczej mówi
ą
c, w wyniku którego
mierzona cecha zostaje odwzorowana liczb
ą
.
Odwzorowywanie cech liczbami nale
ż
y uzna
ć
za jedno z podstawowych
zagadnie
ń
metrologii.
W tym miejscu tylko zarysujemy kwesti
ę
znaczenia liczb w metrologii.
Zapytajmy o cel prowadzenia pomiarów. Na pytanie - Dlaczego człowiek mierzy? -
indagowani studenci reaguj
ą
na pocz
ą
tku
ś
miechem, traktuj
ą
c pytanie jako
trywialne do granic przyzwoito
ś
ci. Zach
ę
cani jednak do konkretnej odpowiedzi
łatwo popadaj
ą
w
ś
mieszno
ść
, mówi
ą
c np. „Po to by wiedzie
ć
ile?” albo „By
wiedzie
ć
ile woltów”, itp., co okazuje si
ę
nagle dla nich samych odpowiedzi
ą
„nie
na poziomie”. Ze zrozumieniem przyjmuj
ą
jako prawdziw
ą
tez
ę
,
ż
e do pomiarów
zmusza człowieka
ż
yciowa konieczno
ść
dokonywania porówna
ń
rzeczy i zjawisk.
Porównania te mog
ą
by
ć
w nielicznych przypadkach zgoła prymitywne, obywaj
ą
ce
si
ę
bez liczb (przykładanie do siebie dwóch przedmiotów - rys. 2, rozpoczynanie
biegu przez zawodników ze wspólnej linii startu, itp.). Znakomita wi
ę
kszo
ść
porówna
ń
, je
ś
li ma słu
ż
y
ć
praktycznym celom i da
ć
w rezultacie trwały wynik musi
odpowiedzie
ć
na pytania: „Ile razy?” albo „O ile?”. Odpowiedzi
ą
na nie mo
ż
e by
ć
tylko liczba, uzyskana w wyniku podzielenia lub odj
ę
cia od siebie dwóch innych
liczb przypisanych pierwotnie
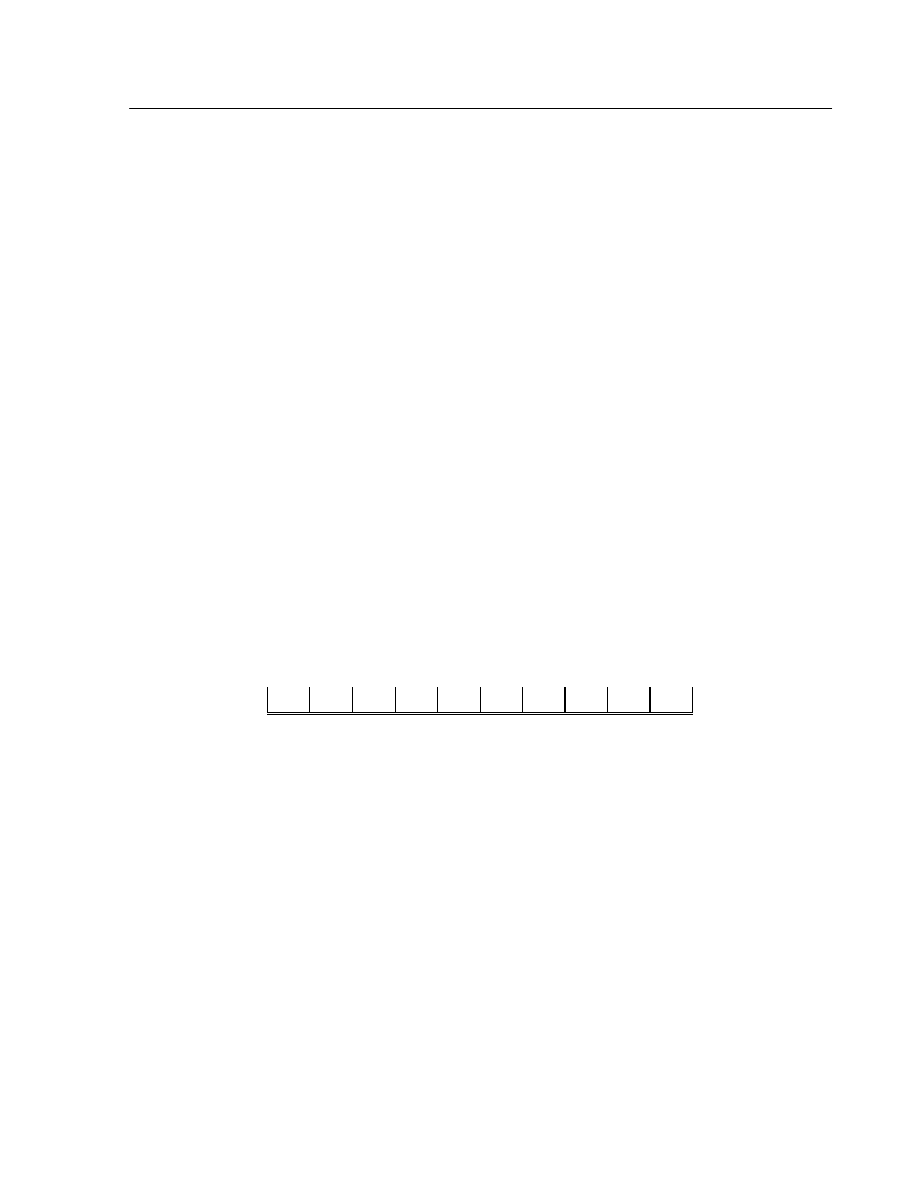
Ć
wicz. Nr 11 Podstawowe zagadnienia metrologii
5
porównywanym cechom. W
ś
wietle tego rozumowania oczywiste staje si
ę
znaczenie
liczb w metrologii.
Warto w tym miejscu przytoczy
ć
my
ś
l znakomitego i wielce dla nauki
zasłu
ż
onego Williama Thomsona (pó
ź
niejszego lorda Kelvina), który powiedział:
„Zaprawd
ę
powiadam wam, je
ś
li to o czym mówicie potraficie zmierzy
ć
i wyrazi
ć
przy pomocy liczb, to wiecie o czym mówicie, w przeciwnym razie wasza wiedza jest
jałowa i pró
ż
na”
Do
ś
wiadczenia b
ę
d
ą
ce pomiarami dokonuj
ą
si
ę
według kilku ogólnych zasad,
zwanych ogólnymi metodami pomiarowymi.
1.4. Skala pomiarowa
W praktyce pomiary, zarówno laboratoryjne jak i przemysłowe odbywaj
ą
si
ę
przy u
ż
yciu skal pomiarowych.
Skala pomiarowa jest uporz
ą
dkowanym zbiorem W warto
ś
ci wzorcowych
w
i
danej wielko
ś
ci mierzalnej.
Bliskim dla wszystkich modelem matematycznym skali pomiarowej jest
pokazana na rys.1 o
ś
liczbowa z ustalonym punktem zerowym i odległo
ś
ci
ą
jednostkow
ą
.
0 1 2 3 4 5 6 7 8 9 10
Rys.1. Model matematyczny skali pomiarowej
Taki obraz skali pomiarowej spotykamy cz
ę
sto, kojarzy nam si
ę
ona ze
szkoln
ą
linijk
ą
, na której naniesiona została podziałka milimetrowa. Podobna do niej
jest podziałka elektrycznego miernika wskazówkowego. Skala pomiarowa zawarta
w przyrz
ą
dach cyfrowych nie jest ju
ż
tak oczywista, bo nie jest dana jawnie w
postaci, do której przywykli
ś
my, nie mniej istnieje. Tworz
ą
j
ą
parametry układów
elektronicznych wchodz
ą
cych w skład przyrz
ą
du, na przykład współczynnik
wzmocnienia wzmacniacza operacyjnego, cz
ę
stotliwo
ść
generatora kwarcowego,
pojemno
ść
licznika impulsów, itp. U
ż
ytkownik nie widzi tej skali, a dodatku proces
porównywania wielko
ś
ci mierzonej z t
ą
skal
ą
nie jest dla niego widoczny, tak jak w
przypadku pomiaru z u
ż
yciem przyrz
ą
du
Ć
wicz. Nr 11 Podstawowe zagadnienia metrologii
6
wskazówkowego, kiedy to mo
ż
emy niemal osobi
ś
cie uczestniczy
ć
w procesie
pomiarowym.
Te najprostsze i najcz
ę ś
ciej stosowane skale pomiarowe nie wystarczaj
ą
do
pomiaru wszystkich wielko
ś
ci, które trzeba mierzy
ć
w praktyce. Skal pomiarowych
jest wi
ę
cej i mo
ż
na podziwia
ć
niejednokrotnie ich wyrafinowan
ą
ró
ż
norodno
ś ć
. W
tym miejscu nie b
ę
dziemy si
ę
nimi zajmowali. Wyczerpuj
ą
cy materiał na ten temat
znale
ź ć
mo
ż
na w podr
ę
czniku [4].
1.5. Zasady tworzenia skali pomiarowej
Tworzenie skali pomiarowej wymaga dwóch zasadniczych kroków.
1. Powołania do
ż
ycia jednostki miary
2. Obmy
ś
lenie i realizacja do
ś
wiadczenia, w wyniku którego mo
ż
na byłoby
stwierdzi
ć
równowa
ż
no
ś ć
dwóch cech tego samego rodzaju .
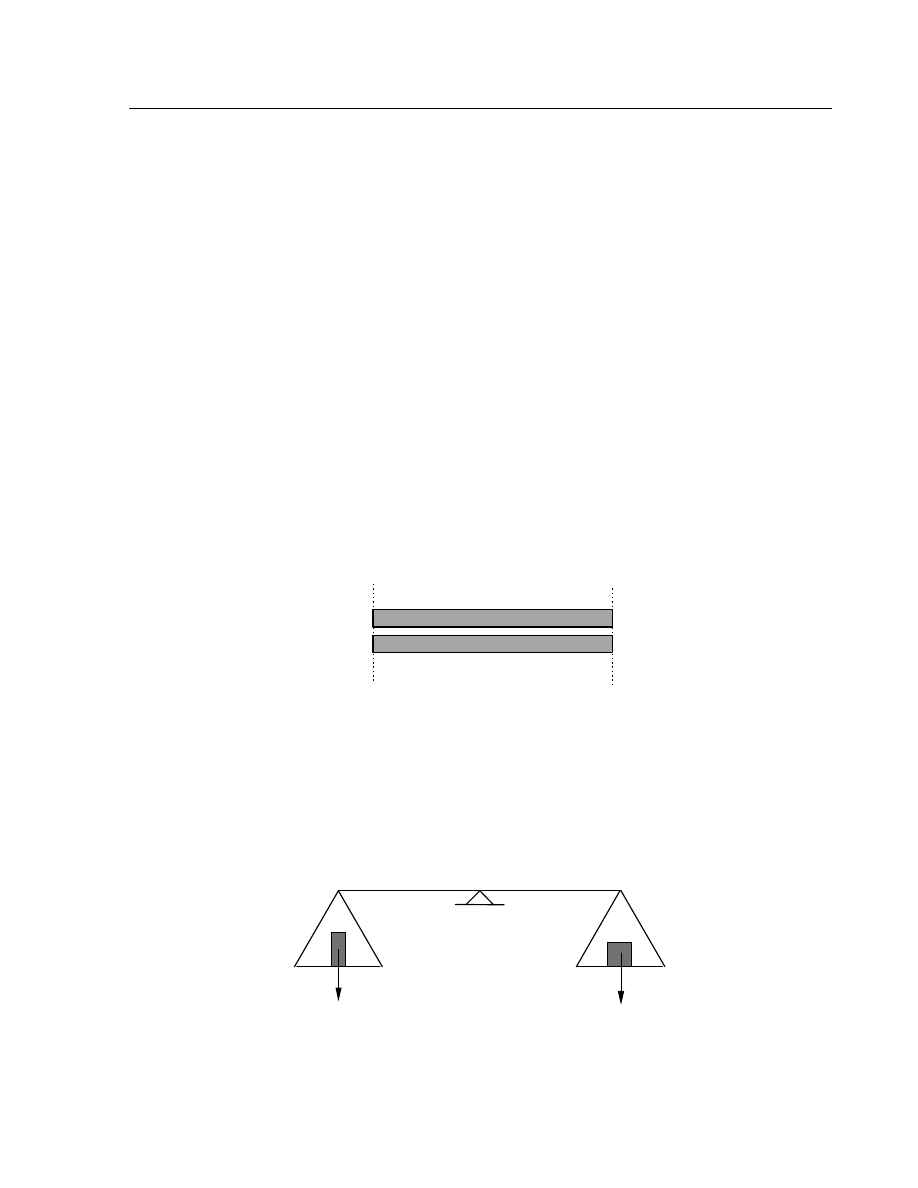
Proste do
ś
wiadczenie pozwalaj
ą
ce stwierdzi
ć
równowa
ż
no
ś ć
dwóch długo
ś
ci
l
1
, l
2
, polega na odpowiednim przyło
ż
eniu do siebie ciał, w których zawarte s
ą
te
cechy (rys.2).
l
1
l
2
Rys.2. Do
ś
wiadczenie pozwalaj
ą
ce stwierdzi
ć
równowa
ż
no
ś ć
dwóch długo
ś
ci
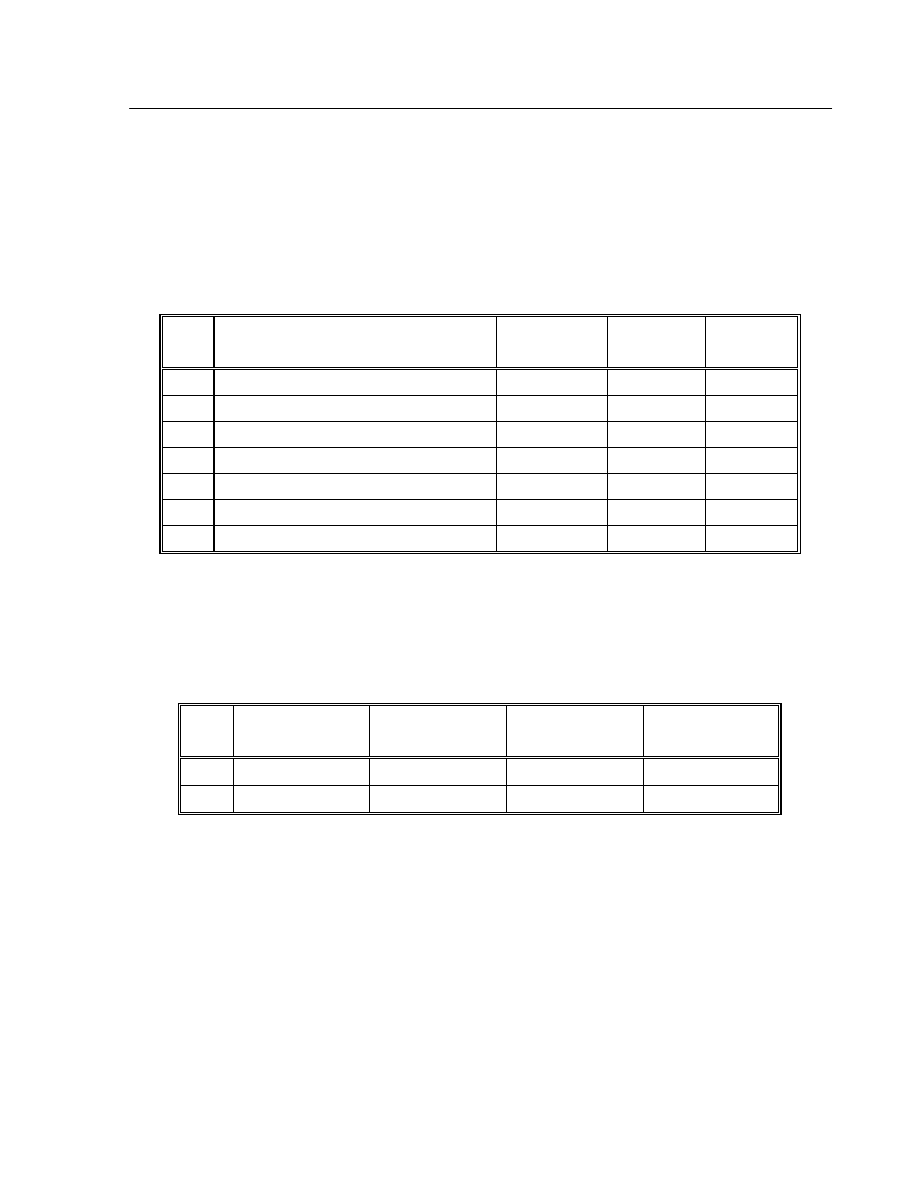
O wiele bardziej skomplikowanym do
ś
wiadczeniem jest to, które pozwala na
stwierdzenie równowa
ż
no
ś
ci dwóch mas. W do
ś
wiadczeniu tym (rys.3)
wykorzystuje si
ę
zasad
ę
d
ź
wigni dwustronnej odkrytej przez Archimedesa oraz
jedn
ą
z zasad dynamiki Newtona.
m
2
m
1
r
2
r
1
F
2
F
1
Rys.3. Waga szalkowa pozwala stwierdzi
ć
równowa
ż
no
ś ć
mas dwóch ciał

Ć
wicz. Nr 11 Podstawowe zagadnienia metrologii
7
Waga znajduje si
ę
w równowadze dzi
ę
ki równo
ś
ci momentów sił
F r
F r
1 1
2 2
=
Siły mo
ż
na przedstawi
ć
jako iloczyny odpowiednich mas i przy
ś
pieszenia
ziemskiego, st
ą
d,
m gr
m gr
1
1
2
2
=
Je
ś
li ramiona wagi s
ą
sobie równe, tzn.
r
r
1
2
=
, otrzymuje si
ę
równo
ś ć
:
m
m
1
2
=
Przedstawione tu do
ś
wiadczenie przeprowadzone zgodnie z uznanymi prawami
fizyki pozwala z niezachwian
ą
pewno
ś
ci
ą
stwierdzi
ć
równowa
ż
no
ś ć
dwóch mas i
sta
ć
si
ę
podstaw
ą
do stworzenia skali pomiarowej mas.
W przypadku tworzenia skal pomiarowych innych wielko
ś
ci mierzalnych
wymagane do
ś
wiadczenia s
ą
bardziej skomplikowane, nie mniej zasada tworzenia
skali wymaga wykonania wymienionych dwóch zasadniczych kroków.
Celowe byłoby, aby czytelnik sam obmy
ś
lił do
ś
wiadczenie, w wyniku którego
mo
ż
liwe jest stwierdzenie równowa
ż
no
ś
ci nat
ęż
e
ń
dwóch pr
ą
dów stałych.
1.6. Wielko
ś
ci podstawowe
Wyja
ś
nimy w tym punkcie przyczyn
ę
, dla której cz
ęś ć
wielko
ś
ci mierzalnych
nie ma swoich definicji w postaci równa
ń
matematycznych.
Je
ż
eli przez R oznaczymy liczb
ę
niezale
ż
nych równa
ń
(jest ich, jak kto
ś
policzył, ok. 800) b
ę
d
ą
cych prawami fizyki (niezale
ż
nych, tzn. takich, z których
ż
adnego nie mo
ż
na otrzyma
ć
w wyniku przekształcenia innego), przez W natomiast
liczb
ę
wielko
ś
ci mierzalnych wyst
ę
puj
ą
cych w tych równaniach, to okazuje si
ę
ż
e
wielko
ś
ci mierzalnych jest wi
ę
cej ni
ż
równa
ń
(W > R). Je
ż
eli wi
ę
c wielko
ś
ci
mierzalne potraktowa
ć
jako niewiadome, układ R równa
ń
oka
ż
e si
ę
nierozwi
ą
zywalny. Jedyn
ą
rad
ą
jest w tym przypadku przyj
ę
cie pewnej liczby
niewiadomych (wielko
ś
ci mierzalnych) za parametry. Minimalna liczba tych
parametrów musi oczywi
ś
cie wynosi
ć
P, gdzie:
P = W - R
Okazuje si
ę
,
ż
e liczba P jest dla poszczególnych dziedzin nauki ró
ż
na, np.
mechanika potrzebuje ich tylko trzy:

Ć
wicz. Nr 11 Podstawowe zagadnienia metrologii
8
- masa (m)
- długo
ść
(l)
- czas (t)
Fakt,
ż
e wymienione trzy wielko
ś
ci nie maj
ą
swoich równa
ń
definicyjnych nie
oznacza,
ż
e potrafimy ich mierzy
ć
. Umiemy bowiem tworzy
ć
ich jednostki miar, a
tak
ż
e obmy
ś
la
ć
do
ś
wiadczenia fizyczne pozwalaj
ą
ce stwierdza
ć
równowa
ż
no
ść
dwóch mas, dwóch długo
ś
ci, czy dwóch czasów, w konsekwencji za
ś
tworzy
ć
potrzebne skale pomiarowe.
Masa, długo
ść
i czas nie maj
ą
swoich równa
ń
definicyjnych ale wyst
ę
puj
ą
w
równaniach innych wielko
ś
ci mierzalnych gdzie odgrywaj
ą
bardzo wa
ż
n
ą
role, o
czym powiemy za chwil
ę
.
Dziedzina
elektrotechniki
potrzebuje
natomiast
czterech
wielko
ś
ci
podstawowych:
- masy (m)
- długo
ś
ci (l)
- czasu (t)
- nat
ęż
enia pr
ą
du elektrycznego (i)
Jak wida
ć
wymaga ona oprócz trzech pierwszych jeszcze jednej: wielko
ś
ci
elektrycznej. W przeszło
ś
ci była ni
ą
rezystancja, wybór wielko
ś
ci podstawowych
jest
bowiem
spraw
ą
umowy
i
stanowi
rezultat
ustale
ń
konferencji
mi
ę
dzynarodowych dotycz
ą
cych miar.
Na wielko
ś
ci podstawowe wybiera si
ę
te wielko
ś
ci, dla których mo
ż
liwe jest
budowanie najdokładniejszych wzorców ich jednostek.
Tych kilka wzorców jednostek stanowi bowiem podstaw
ę
do budowy i
weryfikacji olbrzymiej liczby wzorców jednostek pozostałych wielko
ś
ci (wielko
ś
ci
pochodnych). Wszystkie wielko
ś
ci mierzalne wyst
ę
puj
ą
ce w mechanice, czy
elektrotechnice mo
ż
na wyrazi
ć
, przekształcaj
ą
c ich równania definicyjne, przy
pomocy tylko trzech, czy czterech wymienionych wy
ż
ej wielko
ś
ci podstawowych.
Rezultatem tego jest wspomniana przed chwil
ą
mo
ż
liwo
ść
budowy, czy weryfikacji
wzorców wielkiej liczby jednostek przy u
ż
yciu zaledwie kilku wzorów jednostek
wielko
ś
ci podstawowych.
Na koniec wypada wyja
ś
ni
ć
jaka liczba wielko
ś
ci podstawowych (bez
równa
ń
definicyjnych) wyst
ę
puje obecnie w nauce. Jest ich siedem, przy czym
liczba ta nie wynika z „matematycznej konieczno
ś
ci” lecz postulatów
reprezentantów pewnych dziedzin nauki, którym przyj
ę
cie pewnych dodatkowych
Ć
wicz. Nr 11 Podstawowe zagadnienia metrologii
9
wielko
ś
ci jako wielko
ś
ci podstawowych ułatwia rozwa
ż
ania teoretyczne w
uprawianych przez nich dziedzinach nauki.
W Tablicy 2 przedstawiono obowi
ą
zuj
ą
ce od 1960 roku (data wprowadzenia
Mi
ę
dzynarodowego Układu Jednostek Miar SI) wielko
ś
ci podstawowe i ich
jednostki.
Tablica 2. Wielko
ś
ci podstawowe i ich jednostki
L.p.
Nazwa wielko
ś
ci
podstawowej
Symbol
wielko
ś
ci
Nazwa
jednostki
Symbol
jednostki
1
długo
ść
l
metr
m
2
masa
m
kilogram
kg
3
czas
t
sekunda
s
4
nat
ę ż
enie pr
ą
du elektrycznego
i
amper
A
5
temperatura termodynamiczna
T
kelwin
K
6
ś
wiatło
ść
j
kandela
cd
7
ilo
ść
materii
n
mol
mol
Ten stosunkowo przejrzysty i spokojny obraz m
ą
ci nieco , niewielka grupa
tzw. wielko
ś
ci uzupełniaj
ą
cych, przedstawionych w Tablicy 3.
Tablica 3. Wielko
ś
ci uzupełniaj
ą
ce i ich jednostki
L.p.
Nazwa
wielko
ś
ci
Symbol
wielko
ś
ci
Nazwa
jednostki
Symbol
jednostki
1
k
ą
t płaski
α
,
β
,
γ
radian
rad
2
k
ą
t bryłowy
ω
,
Ω
steradian
sr
Wyja
ś
nienie w sprawie wielko
ś
ci i jednostek uzupełniaj
ą
cych
Na XX Generalnej Konferencji Miar w 1995 r. została podj
ę
ta
rezolucja H, aby jednostki uzupełniaj
ą
ce: radian i steradian wł
ą
czy
ć
do zbioru jednostek pochodnych
Tym samym znika dziwna grupa wielko
ś
ci uzupełniaj
ą
cych i
ich jednostek.

Ć
wicz. Nr 11 Podstawowe zagadnienia metrologii
10
2. Przebieg
ć
wiczenia
Studenci wykonuj
ą
wskazane ni
ż
ej Zadania, sporz
ą
dzaj
ą
c na bie
ż ą
co stosowne
notatki.
Zadanie 1
1. Wymie
ń
trzy mierzalne cechy przedmiotu wr
ę
czonego ci przez prowadz
ą
cego
ć
wiczenie.
2. Uzasadnij praktyczn
ą
przydatno
ś ć
tych cech.
3. Podaj, je
ś
li potrafisz, definicje tych cech.
4. Podaj ich nazwy.
5. Podaj ich symbole literowe
6. Podaj jednostki miar.
7. Podaj nazwy jednostek.
8. Podaj symbole jednostek.
Zadanie 2
Popularna definicja głosi,
ż
e pomiar jest to porównanie wielko
ś
ci mierzonej z
jej jednostk
ą
. Podaj przynajmniej jeden przykład pomiaru odbywaj
ą
cego si
ę
dokładnie według tej definicji.
Zadanie 3
Przekształ
ć
podane ni
ż
ej równanie, wyra
ż
aj
ą
ce moc czynn
ą
pr
ą
du zmiennego,
do postaci, w której wyst
ę
puj
ą
tylko wielko
ś
ci podstawowe.
R
U
P
sk
2
=
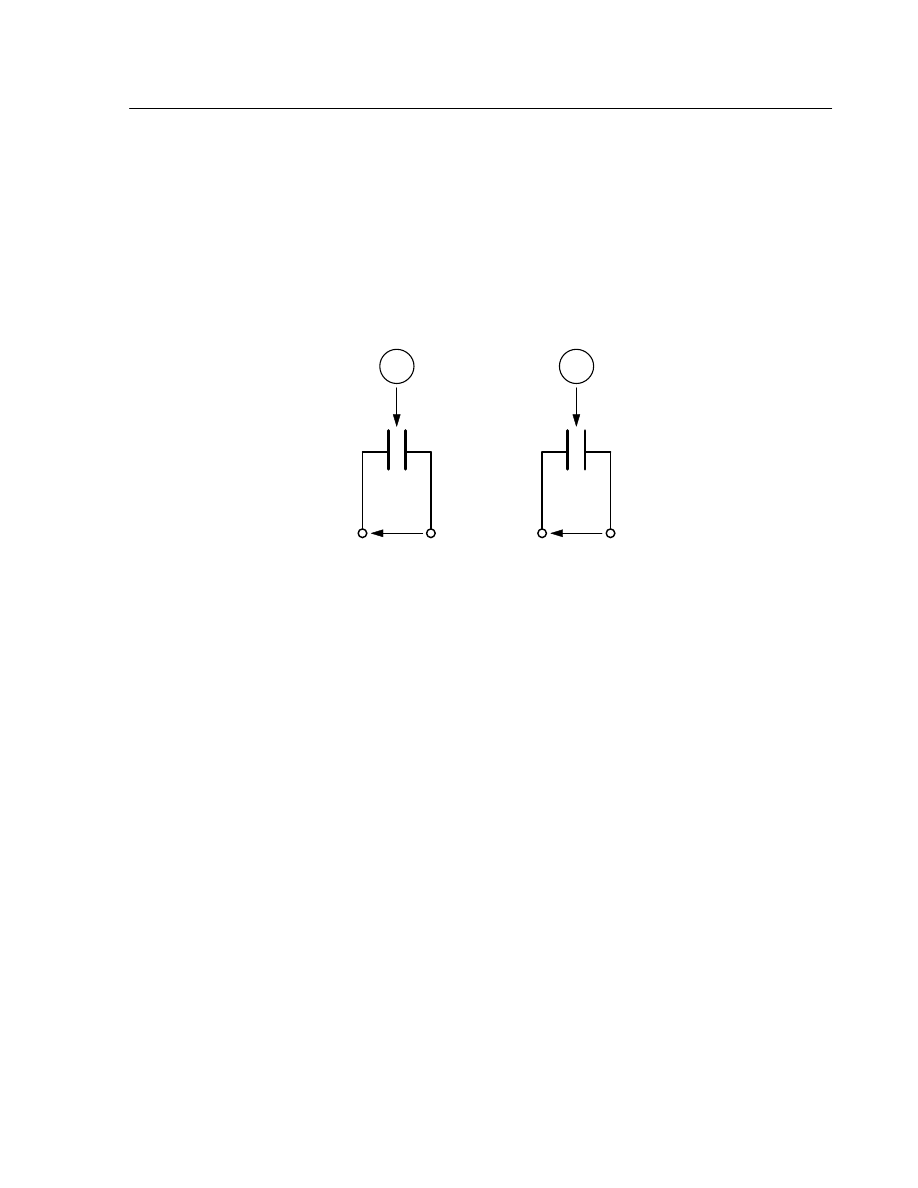
Ć
wicz. Nr 11 Podstawowe zagadnienia metrologii
11
Zadanie 4
Do dwóch kondensatorów C
1
, C
2
(rys.5) doprowadzono jednakowe ładunki
elektryczne q. Który, twoim zdaniem kondensator ma wi
ę
ksz
ą
pojemno
ś ć
elektryczn
ą
, je
ż
eli w jednym z nich ładunek q wywołał powstanie mi
ę
dzy okładkami
napi
ę
cie o warto
ś
ci 1V, za
ś
w drugim 2V? Nale
ż
y przeprowadzi
ć
logiczny wywód,
a nie posługiwa
ć
si
ę
definicj
ą
pojemno
ś
ci elektrycznej.
+
C
1
U
1
=1V
q
+
C
2
U
1
=2V
q
Rys.5. Schemat układu do zadania 2
Zadanie 5
Wyja
ś
nij, według jakiej ogólnej zasady, Twoim zdaniem, zegar mechaniczny
mierzy czas ?
Wskazówka: Czy zmiana poło
ż
enia dowolnej masy m mo
ż
e odby
ć
si
ę
w
czasie zerowym (praca, moc) ?
3. Pytania i zadania kontrolne
1. Na czym polega identyfikacja cech
2. Podaj okre
ś
lenie wielko
ś
ci mierzalnej
3. Podaj okre
ś
lenie jednostki miary
4. Podaj okre
ś
lenie pomiaru
5. Podaj okre
ś
lenie wielko
ś
ci podstawowej
6. Jakie znaczenie maj
ą
wielko
ś
ci podstawowe?

Ć
wicz. Nr 11 Podstawowe zagadnienia metrologii
12
7. Podaj okre
ś
lenie skali pomiarowej
8. Podaj zasady tworzenia skali pomiarowej
9. Podaj okre
ś
lenie pomiaru
10.Dlaczego cz
ę ść
wielko
ś
ci mierzalnych nie ma swoich równa
ń
definicyjnych?
4. Literatura
1. Jaworski J. Matematyczne podstawy metrologii WNT, Warszawa 1979
2. Jaworski J., Morawski R., Ol
ę
dzki J. Wst
ę
p do metrologii i techniki
eksperymentu WNT, Warszawa 1992
3. Piotrowski J. Podstawy metrologii PWN, Warszawa 1976
4. Kubisa S. Podstawy metrologii Wydawnictwo Politechniki Szczeci
ń
skiej,
Szczecin 1995
Wyszukiwarka
Podobne podstrony:
Podstawowe zagadnienia metrologii
11 Podstawowe zagadnienia metrologii
Modul 5 Podstawowe zagadnienia wspolczesnej gospodarki pienieznej i rynku dobr
lista 4 podstawowe zagadnienia
Profilaktyka podstawowe zagadnienia
Podstawowe zagadnienia id 36653 Nieznany
podstawowe zagadnienia, rozporządzenia
PODSTAWOWE ZAGADNIENIA PSYCHOLOGII KULTUROWEJ, antropologia kulturowa
L1, Administracja-notatki WSPol, podstawowe zagadnienia logistyki
Tekst 5, Studia PEDAGOGIKA, Podstawowe zagadnienia gerontologii
referat - ostróda, Administracja-notatki WSPol, podstawowe zagadnienia logistyki
lista 7 podstawowe zagadnienia
ORP podstawowe zagadnienia z fizyki jądrowej
podstawowe zagadnienia, akty prawa miejscowego
więcej podobnych podstron