132

4.3.

Modele rozmyte Takagi–Sugeno

Jedną z odmian modeli rozmytych, które okazały się bardzo skuteczne w modelowaniu

obiektów regulacji są modele typu Takagi–Sugeno [37] (czasami nazywane także modelami
Takagi–Sugeno–Kanga). Modele te są złożone z reguł, w następnikach których używa się
funkcji. Ich zaletą jest możliwość opisania zachowania obiektu za pomocą stosunkowo
niewielkiej liczby reguł. Ogólna postać modeli Takagi–Sugeno jest więc następująca:

Reguła i: jeśli

poprzednik

jest

i

i

jest

4

4

4

4

3

4

4

4

4

2

1

K

i

n

n

i

X

x

X

x

1

1

, to

4

4

4

3

4

4

4

2

1

K

następnik

)

,

,

(

1

n

i

i

x

x

f

y

=

,

( 4.34)

gdzie y

i

są wyjściami następników. Najczęściej w następnikach używa się funkcji liniowych.

Mają więc one postać:

i

n

j

j

i

j

i

a

x

a

y

0

1

+

⋅

=

∑

=

,

( 4.35)

gdzie

i

j

a

(j = 0,…,n, i = 1,…,l) są parametrami modelu, l jest liczbą reguł z których złożony

jest model rozmyty. Zastosowanie następników liniowych upraszcza model. Co więcej, łatwo
jest dokonać identyfikacji ich parametrów korzystając z dobrze znanych metod. Następniki
reguł, ponieważ mogą być interpretowane jako modele opisujące zachowanie obiektu wokół
pewnych punktów pracy, są nazywane modelami lokalnymi.

W celu obliczenia wartości wyjściowej modelu rozmytego Takagi–Sugeno, należy

skorzystać z następującego wzoru:

∑

∑

=

=

⋅

=

l

i

i

l

i

i

i

w

y

w

y

1

1

,

( 4.36)

gdzie w

i

(i = 1,…,l) są siłami odpalenia poszczególnych reguł. Wyjście modelu jest więc

sumą ważoną wyjść poszczególnych modeli lokalnych. Obliczenie wartości wyjścia modelu
typu Takagi–Sugeno jest więc prostsze niż w przypadku modelu z rozmytymi następnikami.

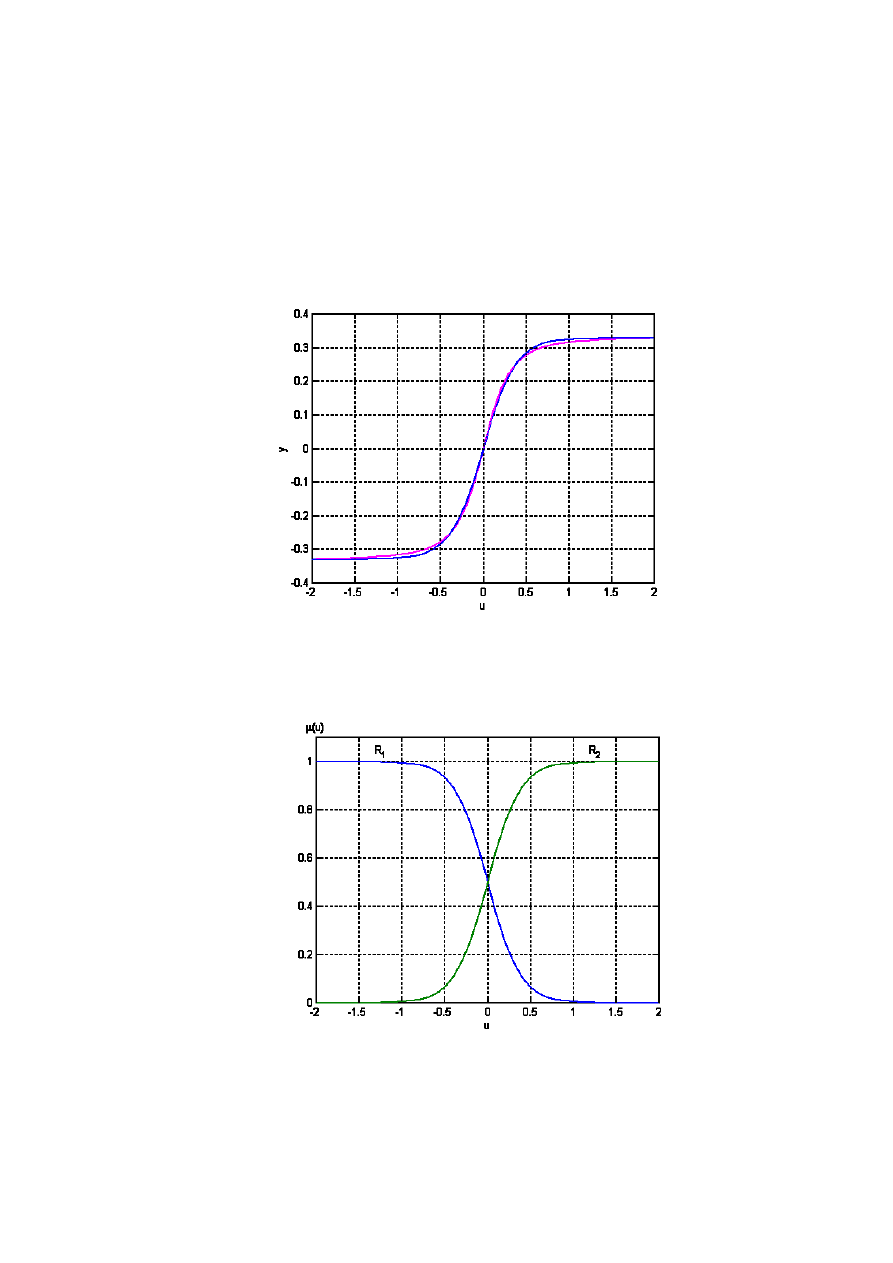
Przykład 4.5

Rozpatrzmy

przykład

rozmytego

modelu

charakterystyki

statycznej

zaworu

przeznaczonego do regulacji przepływu cieczy. Charakterystyka ta jest opisana następującym
wzorem [1]:

2

9

,

0

1

,

0

3163

,

0

u

u

y

⋅

+

⋅

=

,

( 4.37)

gdzie wyjście y jest przepływem przez zawór, a wejście u jest pozycją trzpienia zaworu.
Charakterystyka ta jest przedstawiona na rys. 4.14 linią różową. Zauważmy, że kształt tej
charakterystyki przypomina funkcję sigmoidalną. Spróbujmy użyć modelu rozmytego do
zamodelowania tej charakterystyki. Można przy tym posłużyć się doborem parametrów
modelu wspomaganym komputerowo. Po takim zabiegu, otrzymano funkcje przynależności
pokazane na rys. 4.15. Model rozmyty jest złożony z następujących dwóch reguł [22]:

133

Reguła 1: jeśli u jest R

1

, to

y

= –0,3289,

Reguła 2: jeśli u jest R

2

, to

y

= 0,3289.

Model ten choć prosty, zaskakująco dobrze oddaje modelowaną nieliniowość (linia niebieska
na rys. 4.14).

Rys. 4.14. Charakterystyka statyczna zaworu regulacyjnego;

oryginalna – linia różowa, z modelu rozmytego – linia niebieska

Rys. 4.15. Funkcje przynależności w modelu rozmytym

charakterystyki statycznej zaworu regulacyjnego

134

Przykład 4.6

Rozpatrzmy teraz przypadek dynamicznego modelu typu Takagi–Sugeno. Załóżmy, że jest

to model dyskretny o jednym wejściu i jednym wyjściu, wykorzystujący wartości sygnałów
wejściowego i wyjściowego procesu w przeszłości oraz równania różnicowe w następnikach.
W takim razie model ten jest złożony z następujących reguł:

Reguła i: jeśli

i

m

m

k

i

k

i

n

n

k

i

k

C

u

C

u

B

y

B

y

jest

i

i

jest

i

jest

i

i

jest

1

1

1

1

+

−

+

−

K

K

to

1

1

1

1

1

+

−

+

−

+

⋅

+

+

⋅

+

⋅

+

+

⋅

=

m

k

i

m

k

i

n

k

i

n

k

i

i

k

u

c

u

c

y

b

y

b

y

K

K

,

( 4.38)

gdzie

i

m

i

i

n

i

c

c

b

b

,

,

,

,

,

1

1

K

K

(i = 1,…,l) są współczynnikami modeli lokalnych, y

k

jest wartością

wyjścia obiektu regulacji w chwili k, u

k

jest wartością wejścia w chwili k,

i

B

1

,…,

i

n

B

,

i

C

1

,…,

i

m

C

są zbiorami rozmytymi. Zauważmy, że modele lokalne są liniowe

(najczęściej takie są używane w praktyce) i mogą być zidentyfikowane na podstawie próbek
zarejestrowanych w okolicach kilku punktów pracy podczas eksperymentów prowadzonych
na realnym obiekcie (często stosowane podejście).

Powróćmy teraz do ogólnej postaci modeli typu Takagi–Sugeno. Zwróćmy uwagę na to, że

zastosowanie wzoru ( 4.36) jest równoważne obliczaniu następującej sumy:

0

1

~

~

a

x

a

y

n

j

j

j

+

⋅

=

∑

=

,

( 4.39)

∑

∑

=

=

⋅

=

l

i

i

l

i

i

j

i

j

w

a

w

a

1

1

~

,

gdzie

j

a

~ jest sumą ważoną odpowiednich parametrów modeli lokalnych. W celu

uproszczenia zapisu zwykle wprowadza się wagi znormalizowane, tzn.:

∑

=

=

l

i

i

i

i

w

w

w

1

~

.

( 4.40)

Przykład 4.7

Wróćmy do poprzedniego przykładu. Wyjście rozmytego modelu dynamicznego będzie w

takim razie opisane następującą zależnością:

1

1

1

1

1

~

~

~

~

+

−

+

−

+

⋅

+

+

⋅

+

⋅

+

+

⋅

=

m

k

m

k

n

k

n

k

k

u

c

u

c

y

b

y

b

y

K

K

,

( 4.41)

gdzie

∑

=

⋅

=

l

i

i

j

i

j

b

w

b

1

~

~

,

∑

=

⋅

=

l

i

i

j

i

j

c

w

c

1

~

~

.

Tego typu model można więc traktować jako model liniowy z parametrami zmiennymi w
czasie. Dlatego też modele Takagi–Sugeno nazywa się czasem modelami quasi–liniowymi.

135

4.3.1.

Przedstawienie modelu Takagi–Sugeno w postaci sieci neuronowej

Modele rozmyte można przedstawić w postaci rozmytych sieci neuronowych (ang. Fuzzy

Neural Networks – FNN), zob. np. [29, 31, 38]. Można z nich skorzystać w celu identyfikacji
modeli rozmytych. Przypomnijmy, ogólną postać modeli rozmytych typu Takagi–Sugeno.
Model takiego typu jest złożony z zestawu następujących reguł (przy założeniu następników
opisanych funkcją liniową):

Reguła i: jeśli

jest

i

i

jest

i

n

n

i

X

x

X

x

K

1

1

, to

i

n

j

j

i

j

i

a

x

a

y

0

1

+

⋅

=

∑

=

.

( 4.42)

Wyjście modelu rozmytego typu Takagi–Sugeno jest z kolei dane wzorem:

∑

=

⋅

=

l

i

i

i

y

w

y

1

~

,

( 4.43)

gdzie

i

w

~ są znormalizowanymi wagami. W takim razie, ogólną strukturę rozmytej sieci

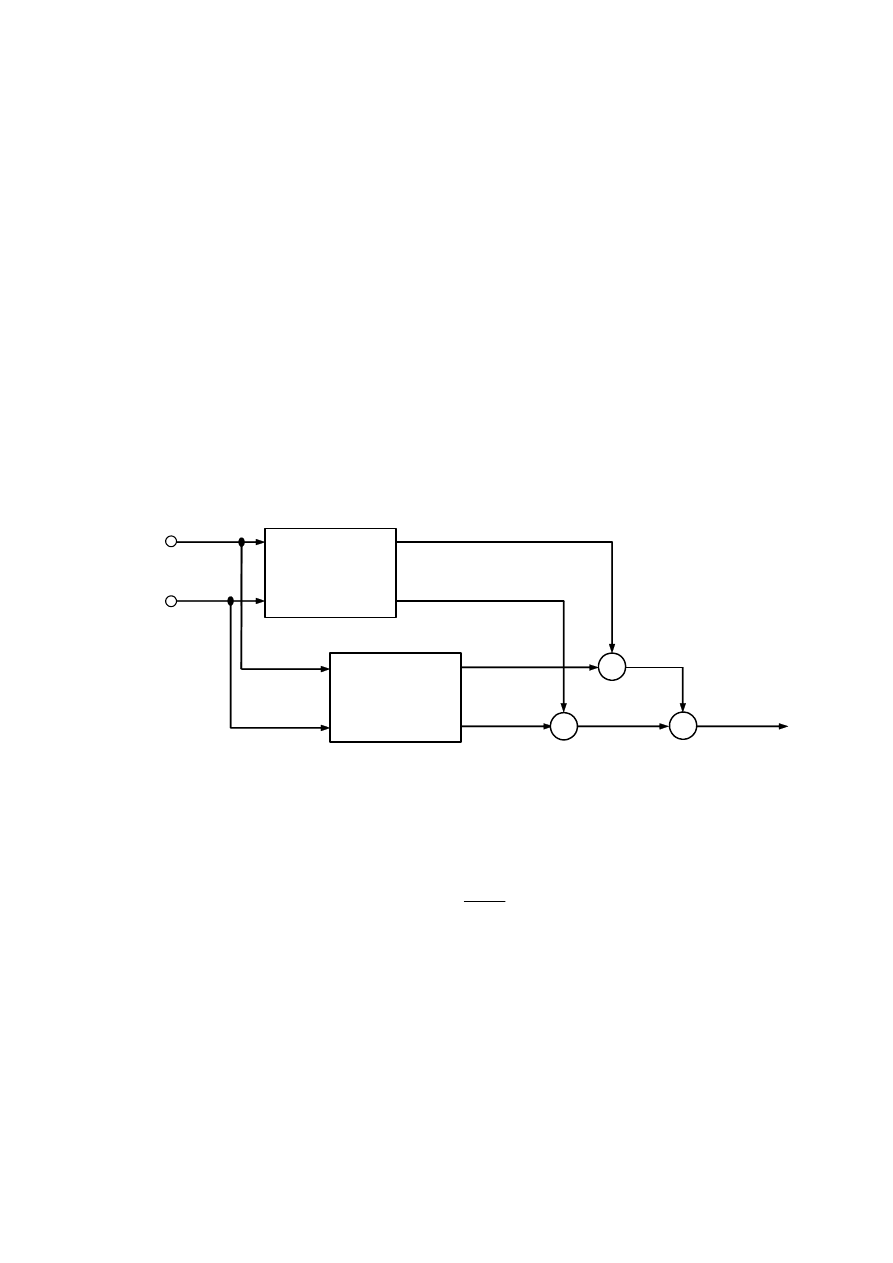
neuronowej odzwierciedlającej model rozmyty z wyjściem opisanym równaniem ( 4.43)
można przedstawić, jak na rys. 4.16.

x

1

Neuronowy

model

poprzedników

x

n

::::

::::

Neuronowy

model

następników

y

1

y

l

::::

::::

::::

::::

x

x

w

1

w

l

::::

::::

+

y

~

~

::::

::::

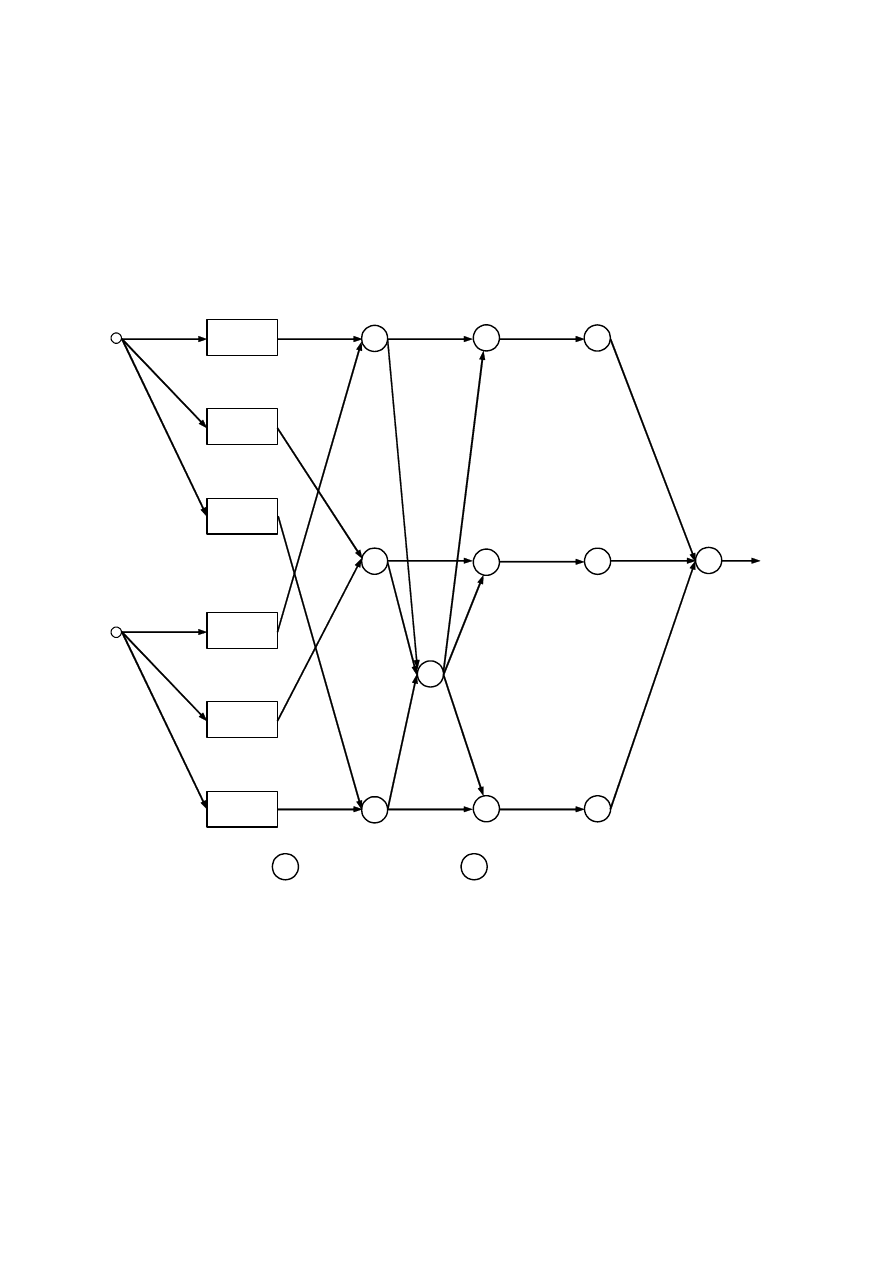
Rys. 4.16. Ogólna struktura rozmytej sieci neuronowej

Neuronowy model poprzedników

Przypomnijmy, że znormalizowane wagi są opisane wzorem:

∑

=

=

l

i

i

i

i

w

w

w

1

~

,

( 4.44)

gdzie poszczególne wagi w

i

, przy założeniu, że jako operatora koniunkcji użyto mnożenia, są

iloczynem wartości funkcji przynależności:

∏

=

=

n

j

j

X

i

x

w

i

j

1

)

(

µ

.

( 4.45)

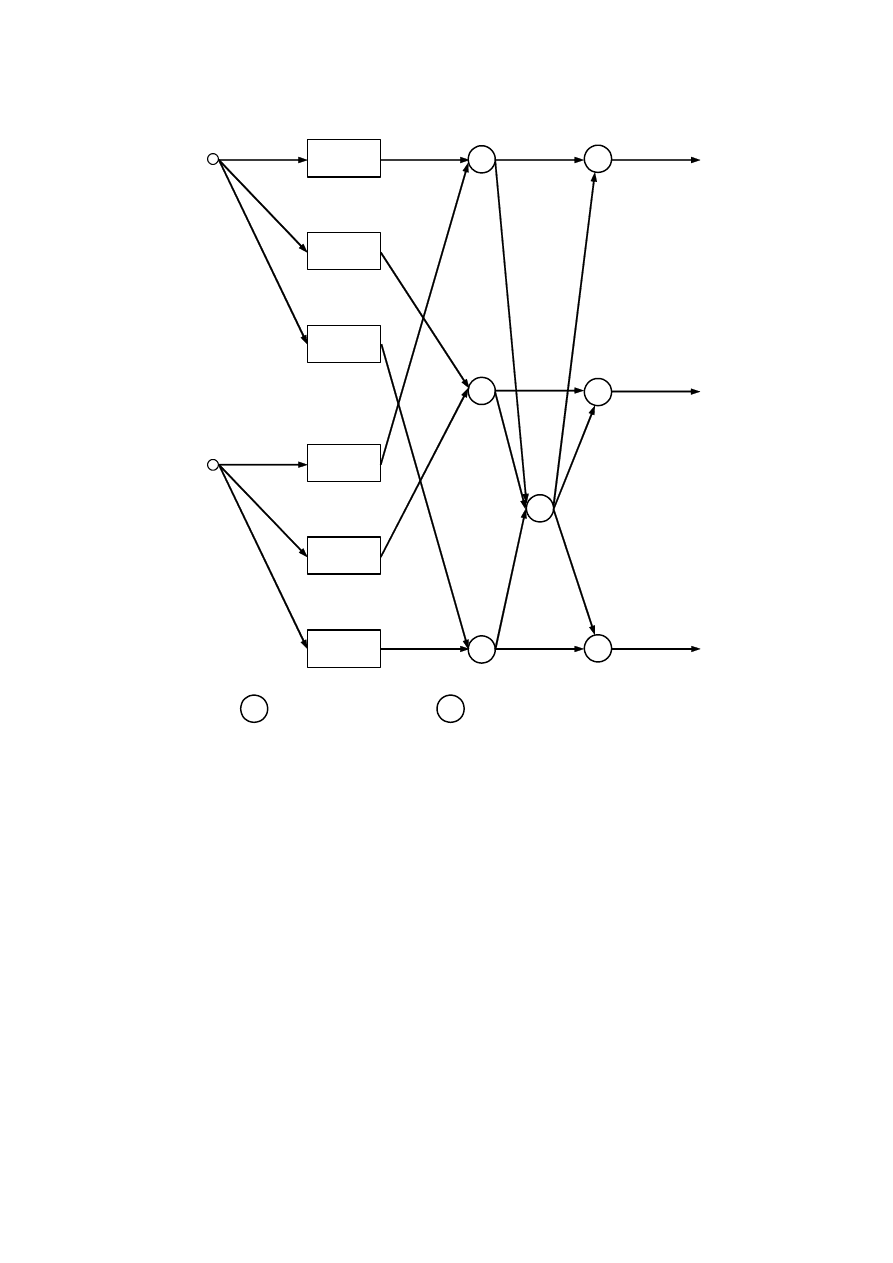
W takim razie struktura neuronowego modelu poprzedników będzie miała postać taką, jak na
rys. 4.17.

136

x

1

::::

::::

::::

::::

::::

::::

::::

::::

x

n

::::

::::

)

(x

1

X

1
1

µ

)

(x

1

X

i
1

µ

)

(x

1

X

l
1

µ

::::

::::

::::

::::

)

(x

n

X

1
n

µ

)

(x

n

X

i
n

µ

)

(x

n

X

l
n

µ

x

x

x

::::

::::

w

1

w

i

w

l

/

/

/

~

w

1

~

w

i

~

w

l

∑

=

l

1

i

i

w

::::

::::

::::

::::

x

– mnożenie

/

– dzielenie

Rys. 4.17. Neuronowy model poprzedników rozmytego modelu Takagi–Sugeno

Zauważmy, że w powyższym modelu neuronowym poprzedników, uczeniu podlegają

parametry funkcji przynależności

)

(

j

X

x

i

j

µ

. Funkcje te zostały oznaczone elementami

prostokątnymi, ponieważ są to elementy bardziej złożone, które można byłoby przedstawić za
pomocą prostszych neuronów. Nie jest to jednak konieczne do przeprowadzenia dalszych
rozważań.

Neuronowy model następników

Przypomnijmy postać następników poszczególnych reguł w rozważanym modelu

rozmytym:

i

n

j

j

i

j

i

a

x

a

y

0

1

+

⋅

=

∑

=

; i = 1,…, l.

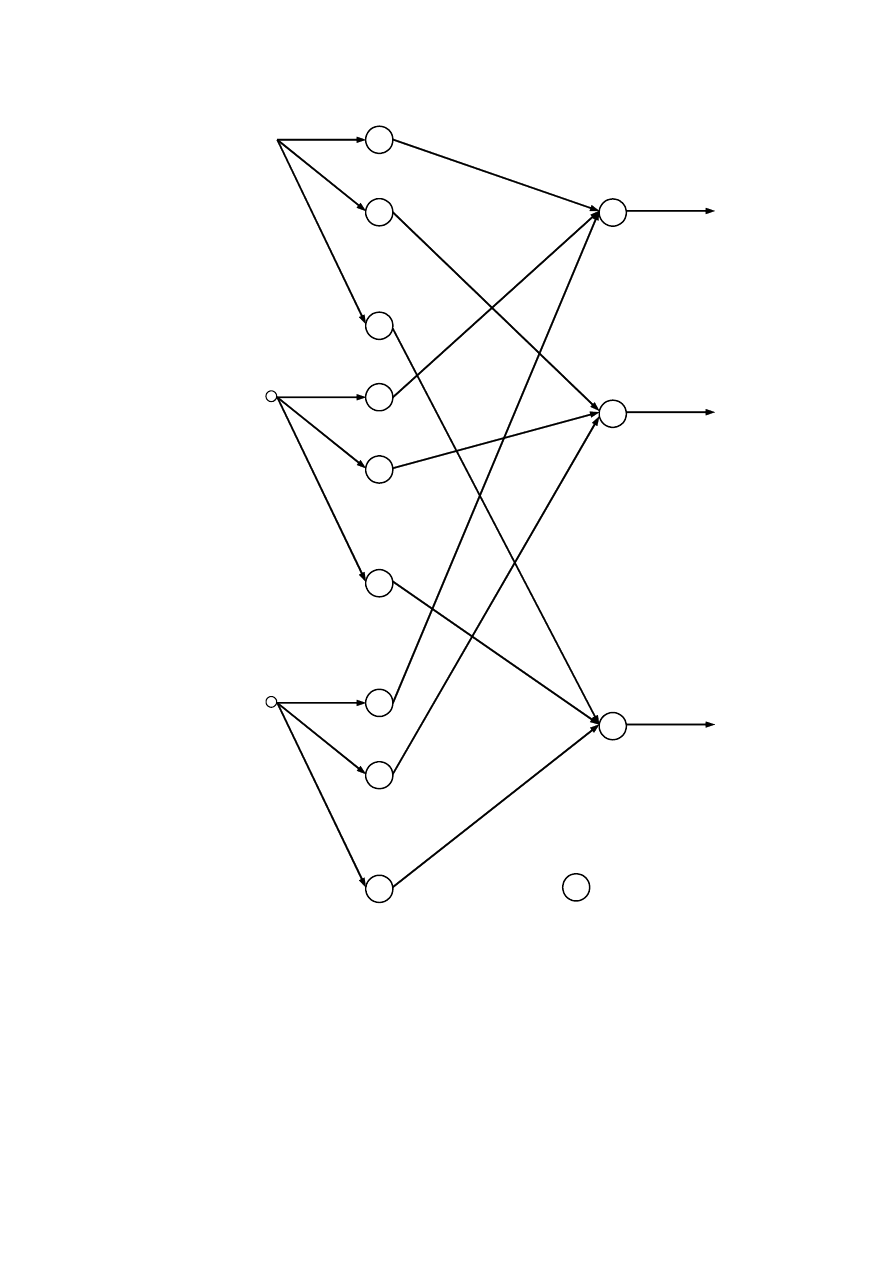
Zauważmy, że jest to zależność liniowa. W takim razie struktura następników reguł
rozważanego modelu Takagi–Sugeno może być przedstawiona jako sztuczna sieć neuronowa
z rys. 4.18. W tym modelu neuronowym, uczeniu podlegają parametry

i

j

a

funkcji liniowych

występujących w następnikach reguł, z których jest złożony model rozmyty.

137

1

x

1

y

1

::::

::::

1

0

a

::::

::::

::::

::::

2
0

a

l
0

a

::::

::::

::::

::::

1
1

a

2

1

a

l
1

a

::::

::::

x

n

::::

::::

1
n

a

2
n

a

l
n

a

::::

::::

::::

::::

y

2

y

l

– neuron liniowy

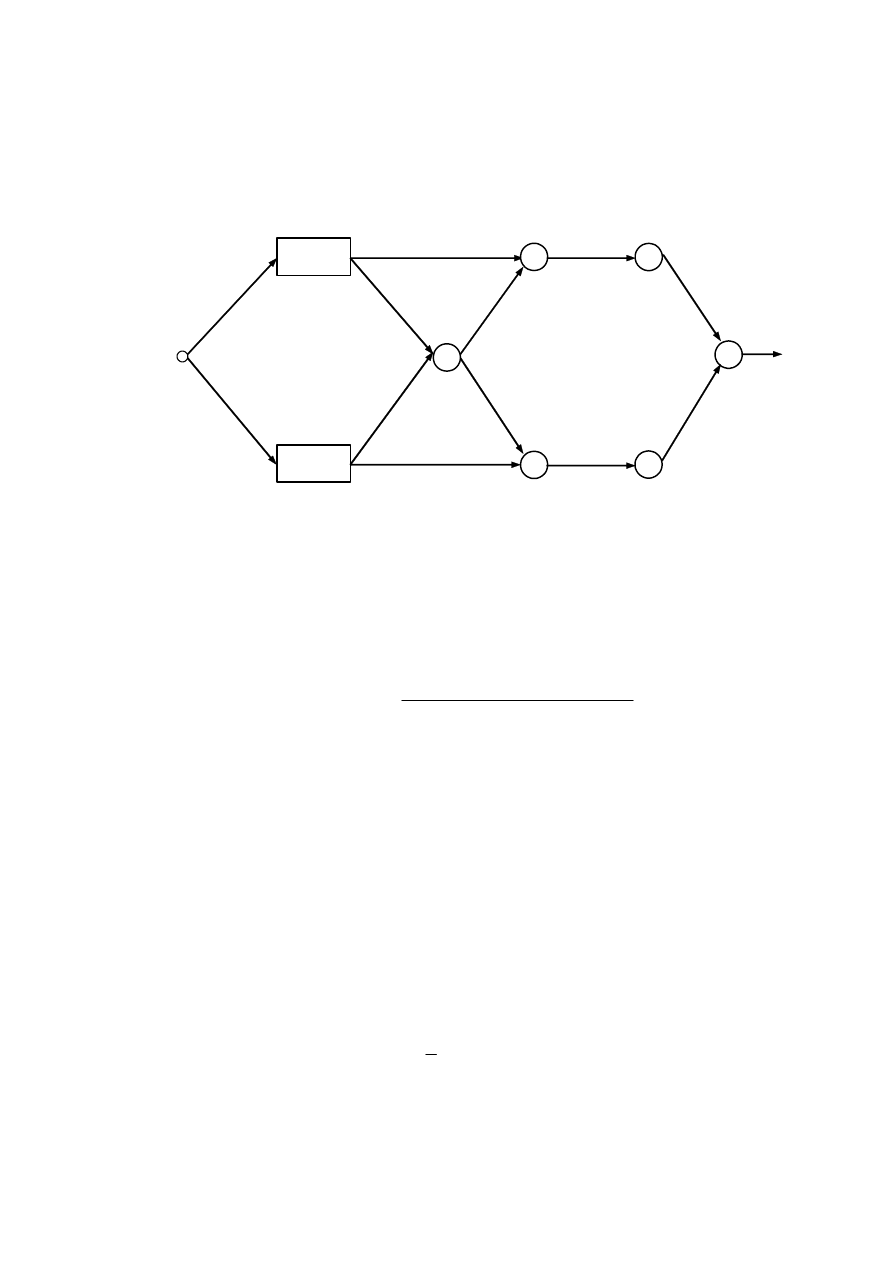
Rys. 4.18. Neuronowy model następników rozmytego modelu Takagi–Sugeno

Przykład 4.8 (rozmyta sieć neuronowa Wanga–Mendela)

W przypadku, gdy następniki w modelu Takagi–Sugeno są stałe, tzn.

i

i

a

y

0

=

,

( 4.46)

model ulega znacznemu uproszczeniu. W takim przypadku, wyjście modelu jest bowiem dane
wzorem:

138

∑

=

⋅

=

l

i

i

i

a

w

y

1

0

~

.

( 4.47)

Także struktura sztucznej sieci neuronowej opisującej taki model znaczenie się upraszcza.
Tego typu model neuronowy jest nazywany modelem Wanga–Mendela a jego postać została
pokazana na rys. 4.19. Parametry modelu, które mogą zostać dobrane dzięki zastosowaniu
mechanizmu uczenia sieci to parametry funkcji przynależności

)

(

j

X

x

i

j

µ

oraz stałe

i

a

0

występujące w następnikach reguł modelu rozmytego.

x

1

::::

::::

::::

::::

::::

::::

::::

::::

x

n

::::

::::

)

(x

1

X

1
1

µ

)

(x

1

X

i
1

µ

)

(x

1

X

l
1

µ

::::

::::

::::

::::

)

(x

n

X

1
n

µ

)

(x

n

X

i
n

µ

)

(x

n

X

l
n

µ

x

x

x

::::

::::

w

1

w

i

w

l

/

/

/

~

w

1

~

w

i

~

w

l

∑

=

l

1

i

i

w

::::

::::

x

– mnożenie

/

– dzielenie

1

0

a

y

i
0

a

l
0

a

::::

::::

Rys. 4.19. Neuronowy model Wanga–Mendela

Przykład 4.9

Rozpatrzmy rozmyty model statyki zaworu z przykładu 4.5. Przypomnijmy, że model ten

jest złożony z następujących dwóch reguł:

Reguła 1: jeśli u jest R

1

, to

3289

,

0

1
0

1

−

=

= a

y

,

Reguła 2: jeśli u jest R

2

, to

3289

,

0

2

0

2

=

= a

y

.

139

W takim razie sztuczna sieć neuronowa opisująca ten model będzie miała postać Wanga–
Mendela. Zauważmy, że założono sigmoidalne funkcje przynależności

)

(

1

u

R

µ

oraz

)

(

2

u

R

µ

.

Ponieważ w modelu użyte zostały poprzedniki proste, struktura sieci również jest szczególnie
prosta (nie jest potrzebne użycie mnożenia).

u

(u)

1

R

µ

(u)

2

R

µ

w

1

/

/

~

w

1

1

0

a

y

w

2

~

w

2

2
0

a

Rys. 4.20. Neuronowy model statyki zaworu z przykładu 4.5

4.3.2.

Hybrydowy algorytm uczenia rozmytych sieci neuronowych

Zauważmy, że szczegółowa zależność opisująca wyjście modelu Takagi–Sugeno (a tym

samym wyjście rozmytej sieci neuronowej, za pomocą której można taki model przedstawić)
jest dana następującym wzorem:

∑∏

∑

∑

∏

=

=

=

=

=















+

⋅

⋅

=

l

i

n

j

j

X

l

i

i

n

j

j

i

j

n

j

j

X

n

x

a

x

a

x

x

x

y

i

j

i

j

1

1

1

0

1

1

1

)

(

)

(

)

,

,

(

µ

µ

K

.

( 4.48)

Parametry modelu rozmytego można więc dostroić metodą uczenia rozmytej sieci

neuronowej. W tym celu można wykorzystać dobrze znany mechanizm wstecznej propagacji
błędu. Ze względu na strukturę rozmytej sieci neuronowej (wynikającą ze struktury reguł
modelu rozmytego) możliwe jest zastosowanie dwóch zasadniczych podejść. Pierwsze
podejście polega na dostrajaniu zarówno parametrów poprzedników jak i następników reguł
(wszystkich parametrów podlegających procesowi identyfikacji) analogicznie, jak w
przypadku perceptronu wielowarstwowego. Drugie podejście to algorytm hybrydowy, w
którym parametry poprzedników są dostrajane z wykorzystaniem mechanizmu uczenia zaś
parametry następników – z wykorzystaniem metody najmniejszych kwadratów. Druga z
wymienionych metod daje lepsze rezultaty [29, 38] i na tej właśnie metodzie się teraz
skoncentrujemy.

Podczas uczenia sieci będziemy dążyć do minimalizowania następującej funkcji błędu:

(

)

∑

=

−

=

p

m

d

m

m

y

y

E

1

2

2

1

,

( 4.49)

gdzie p jest liczbą próbek uczących,

)

,

,

(

1

m

n

m

m

m

x

x

y

y

K

=

jest wartością wyjścia uczonej sieci,

d

m

y

jest wartością wyjścia (zmierzoną) obiektu otrzymaną dla zestawu sygnałów wejściowych

140

)

,

,

(

1

m

n

m

x

x

K

. Jak już wspomniano na wstępie, w podejściu hybrydowym, dostrajanie

parametrów poprzedników i następników odbywa się osobno. Dlatego też w algorytmie
można wyróżnić dwa etapy, powtarzane na zmianę podczas procesu uczenia [29].

Etap I

Dla ustalonych (bieżących) wartości parametrów funkcji przynależności, dostrajane są

wartości parametrów następników reguł rozmytych. Zauważmy, że w przypadku przyjęcia
stałych parametrów funkcji przynależności, wyjście modelu rozmytego jest dane wzorem:

∑

∑

=

=















+

⋅

⋅

=

=

l

i

i

n

j

j

i

j

i

n

a

x

a

w

x

x

y

y

1

0

1

1

~

)

,

,

(

K

.

( 4.50)

Powyższy wzór można zapisać w postaci wektorowej:

[

]

























































⋅

⋅

⋅

⋅

⋅

=

l

l

l

n

o

n

l

l

n

l

n

a

a

a

a

a

a

w

x

w

x

w

w

x

w

x

w

y

0

1

1

1

1

1

1

1

1

1

1

~

~

~

~

~

~

M

M

M

K

K

K

.

( 4.51)

Naszym zadaniem jest określenie na podstawie p próbek uczących, którymi dysponujemy,
wartości parametrów

i

j

a

(i = 1,…, l; j = 1,…, n). W idealnym przypadku chcemy otrzymać

następującą równość:

d

y

a

W

=

⋅

,

( 4.52)

gdzie

































⋅

⋅

⋅

⋅

⋅

⋅

⋅

⋅

⋅

⋅

⋅

⋅

=

p

l

p

p

l

p

n

p

l

p

p

p

p

n

p

m

l

m

m

l

m

n

m

l

m

m

m

m

n

m

l

l

n

l

n

w

x

w

x

w

w

x

w

x

w

w

x

w

x

w

w

x

w

x

w

w

x

w

x

w

w

x

w

x

w

~

~

~

~

~

~

~

~

~

~

~

~

~

~

~

~

~

~

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

K

K

K

M

M

O

M

O

M

M

O

M

K

K

K

M

M

O

M

O

M

M

O

M

K

K

K

W

,

























































=

l

l

l

n

o

n

a

a

a

a

a

a

0

1

1

1

1

1

M

M

M

a

,

141

































=

d
p

d

m

d

y

y

y

M

M

1

d

y

.

Zwykle zbiór próbek uczących jest liczny i liczba tych próbek znacznie przekracza liczbę
parametrów zgrupowanych w wektorze a. W związku z tym wartości parametrów
następników reguł rozmytych wyznacza się korzystając z metody najmniejszych kwadratów,
co w programie Matlab sprowadza się do użycia operatora tzw. lewego dzielenia
macierzowego (ang. left matrix divide).

Etap II

Dla bieżących wartości parametrów następników reguł modelu rozmytego oraz funkcji

przynależności, dla poszczególnych próbek uczących wyznacza się wartości wyjściowe
uczonej sieci

)

,

,

(

1

m

n

m

m

m

x

x

y

y

K

=

. Na podstawie tych wartości oraz wartości pożądanych

d

m

y

otrzymuje się wektor błędu:

































−

−

−

=

d
p

p

d

m

m

d

y

y

y

y

y

y

M

M

1

1

ε

.

Następnie korzysta się z mechanizmu wstecznej propagacji błędu. Dostrajanie wartości
parametrów funkcji przynależności wykonuje się, korzystając z wybranej metody
optymalizacji.

Przykład 4.10

Oznaczmy przez c

i

parametry danej funkcji przynależności. Załóżmy także, że funkcja ta

jest różniczkowalna. Wówczas, w przypadku użycia metody najszybszego spadku, otrzymuje
się następujący wzór opisujący iteracyjne dostrajanie tych parametrów:

i

i

i

i

c

E

n

c

n

c

∂

∂

⋅

−

=

+

η

)

(

)

1

(

,

( 4.53)

gdzie n jest numerem kolejnej iteracji uczenia,

i

η

jest współczynnikiem uczenia oraz

(

)

i

i

l

i

i

n

j

j

i

j

d

i

c

w

a

x

a

y

y

c

E

∂

∂

⋅















+

⋅

⋅

−

=

∂

∂

∑ ∑

=

=

~

1

0

1

,

( 4.54)

gdzie

i

i

c

w

∂

∂~

zależy od postaci przyjętej funkcji przynależności.

Uwaga: Gradientowe metody optymalizacji można zastosować w przypadku

różniczkowalnych funkcji przynależności (np. sigmoidalna, dzwonowa, Gaussa). W
przypadku funkcji nieróżniczkowalnych można jednak użyć metod bezgradientowych.