clc

clear

all

N=0.5;

n=2600;

omega=n*2*pi/60;

z1=12;

z2=36;

z3=14;

z4=28;

i=z2/z1;

beta=5*pi/180;

alfa=20*pi/180;

m=1.25*1e-3;

d_z1=z1*m

d_z2=z2*m

d_z3=z3*m

d_z4=z4*m

a=0.03;

b=0.04;

c=0.03;

d_z1 =

0.0150

d_z2 =

0.0450

d_z3 =

0.0175

d_z4 =

0.0350

0.0350

M_2=N/omega*i*1e3

M_2 =

5.5092

P_o2=(M_2/d_z2)*2

% Sila wzdluzna

P_w2=P_o2*tan(beta)

% Sila Promieniowa

P_r2=P_o2*tan(alfa)/cos(beta)

P_o2 =

244.8538

P_w2 =

21.4219

P_r2 =

89.4599

P_o3=M_2/d_z3*2

% Sila Promieniowa

P_r3=P_o3*tan(alfa)

P_o3 =

P_o3 =

629.6240

P_r3 =

229.1644

R_By=(a*P_r2 - P_r3*(a+b) + P_w2*d_z2/2)/ (a+b+c)

% Sila w podporze Ay, suma momentow wzg punktu B

R_Ay=( - P_r3*c + P_r2*(c+b) - P_w2*d_z2/2)/(a+b+c)

% Sprawdzenie

spr=round( R_By + R_Ay - P_r2+P_r3)

if

(spr == 0)

disp(

'Dobrze policzone warunki'

)

else

disp(

'Zle policzone warunki'

)

end

%siła w podporze A wzdluz osi x

R_Bx=-P_w2

R_By =

-128.7572

R_Ay =

-10.9473

spr =

0

Dobrze policzone warunki

R_Bx =

-21.4219

R_Bz=(P_o2*a+P_o3*(a+b))/(a+b+c)

R_Az=(P_o2*(b+c)+P_o3*(c))/(a+b+c)

% Sprawdzenie

spr=round(-R_Bz-R_Az+P_o2+P_o3)

if

(spr == 0)

disp(

'Dobrze policzone warunki'

)

else

disp(

'Zle policzone warunki'

)

end

R_Bz =

514.1929

R_Az =

360.2848

spr =

0

Dobrze policzone warunki

x1=0:0.01:a

Mg_x1_xy=R_Ay*x1

x1 =

0 0.0100 0.0200 0.0300

Mg_x1_xy =

0 -0.1095 -0.2189 -0.3284

x2=a:0.01:(a+b)

x2=a:0.01:(a+b)

Mg_x2_xy= R_Ay*x2 + P_w2*d_z2/2 - P_r2*(x2-a)

x2 =

0.0300 0.0400 0.0500 0.0600 0.0700

Mg_x2_xy =

0.1536 -0.8505 -1.8546 -2.8586 -3.8627

x3=-c:0.01:0

Mg_x3_xy=abs(R_By)*x3

% Przedzial sprawdzajacy

x4=a+b:0.01:(a+b+c)

Mg_x4_xy=R_Ay*x4 +P_w2*d_z2/2- P_r2*(x4-a)+ P_r3*(x4-(a+b))

x3 =

-0.0300 -0.0200 -0.0100 0

Mg_x3_xy =

-3.8627 -2.5751 -1.2876 0

x4 =

0.0700 0.0800 0.0900 0.1000

Mg_x4_xy =

-3.8627 -2.5751 -1.2876 0

x1=0:0.01:a

Mg_x1_xz=-abs(R_Az)*x1

x1 =

x1 =

0 0.0100 0.0200 0.0300

Mg_x1_xz =

0 -3.6028 -7.2057 -10.8085

x2=a:0.01:(a+b)

Mg_x2_xz=-abs(R_Az)*x2+P_o2*(x2-a)

x2 =

0.0300 0.0400 0.0500 0.0600 0.0700

Mg_x2_xz =

-10.8085 -11.9629 -13.1172 -14.2715 -15.4258

x3=-c:0.01:0

Mg_x3_xz=abs(R_Bz)*x3

% Przedzial sprawdzajacy

x4=a+b:0.01:(a+b+c)

Mg_x4_xz=-R_Az*x4 +P_o2*(x4-(a)) + P_o3*(x4-(a+b))

x3 =

-0.0300 -0.0200 -0.0100 0

Mg_x3_xz =

-15.4258 -10.2839 -5.1419 0

x4 =

0.0700 0.0800 0.0900 0.1000

Mg_x4_xz =

-15.4258 -10.2839 -5.1419 0

-15.4258 -10.2839 -5.1419 0

l=[x1,x2,x4]

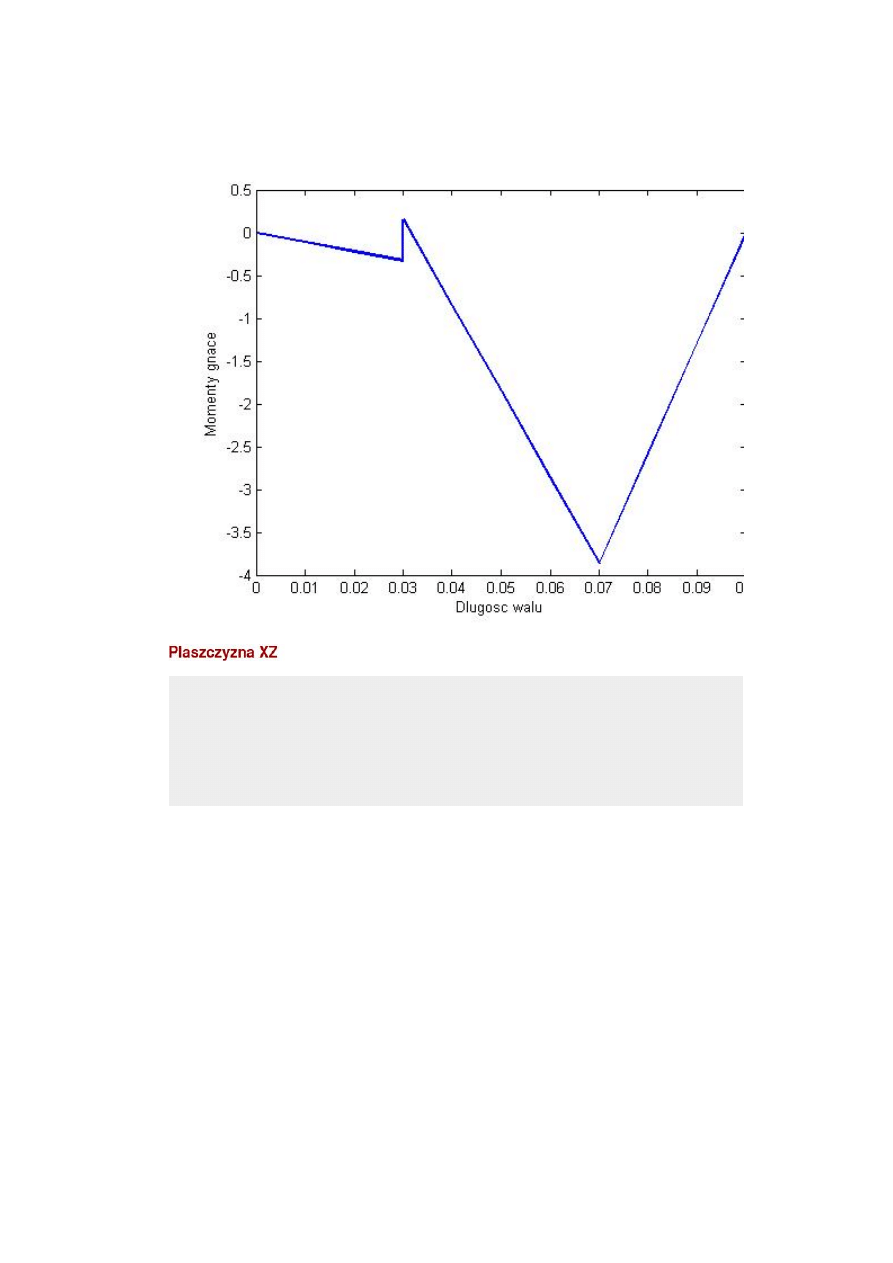
Mg_XY=[Mg_x1_xy,Mg_x2_xy,Mg_x4_xy]

figure(1)

plot(l,Mg_XY,

'linewidth'

,2);

xlabel(

'Dlugosc walu'

)

ylabel(

'Momenty gnace'

)

l =

Columns 1 through 7

0 0.0100 0.0200 0.0300 0.0300 0.0400 0.0500

Columns 8 through 13

0.0600 0.0700 0.0700 0.0800 0.0900 0.1000

Mg_XY =

Columns 1 through 7

0 -0.1095 -0.2189 -0.3284 0.1536 -0.8505 -1.8546

Columns 8 through 13

-2.8586 -3.8627 -3.8627 -2.5751 -1.2876 0

l=[x1,x2,x4]

Mg_XZ=[Mg_x1_xz,Mg_x2_xz,Mg_x4_xz]

figure(2)

plot(l,Mg_XZ,

'linewidth'

,2);

xlabel(

'Dlugosc walu'

)

ylabel(

'Momenty gnace'

)

l =

Columns 1 through 7

0 0.0100 0.0200 0.0300 0.0300 0.0400 0.0500

Columns 8 through 13

0.0600 0.0700 0.0700 0.0800 0.0900 0.1000

Mg_XZ =

Columns 1 through 7

0 -3.6028 -7.2057 -10.8085 -10.8085 -11.9629 -13.1172

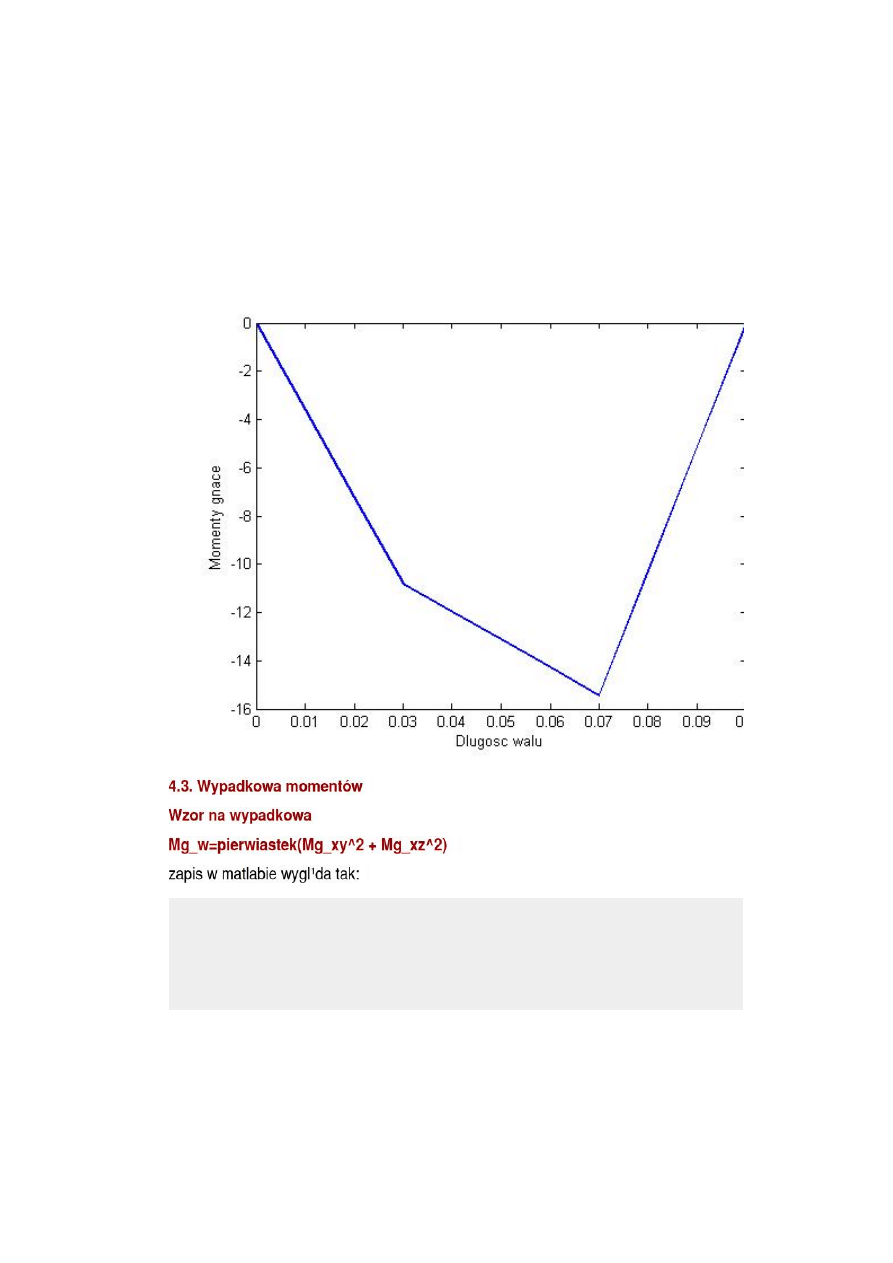
0 -3.6028 -7.2057 -10.8085 -10.8085 -11.9629 -13.1172

Columns 8 through 13

-14.2715 -15.4258 -15.4258 -10.2839 -5.1419 0

Mg_w=sqrt(Mg_XY.^2+Mg_XZ.^2)

figure(3)

plot(l,Mg_XZ,

'linewidth'

,2);

xlabel(

'Dlugosc walu'

)

ylabel(

'Moment gnacy zastepczy'

)

Mg_w =

Columns 1 through 7

0 3.6045 7.2090 10.8135 10.8096 11.9931 13.2476

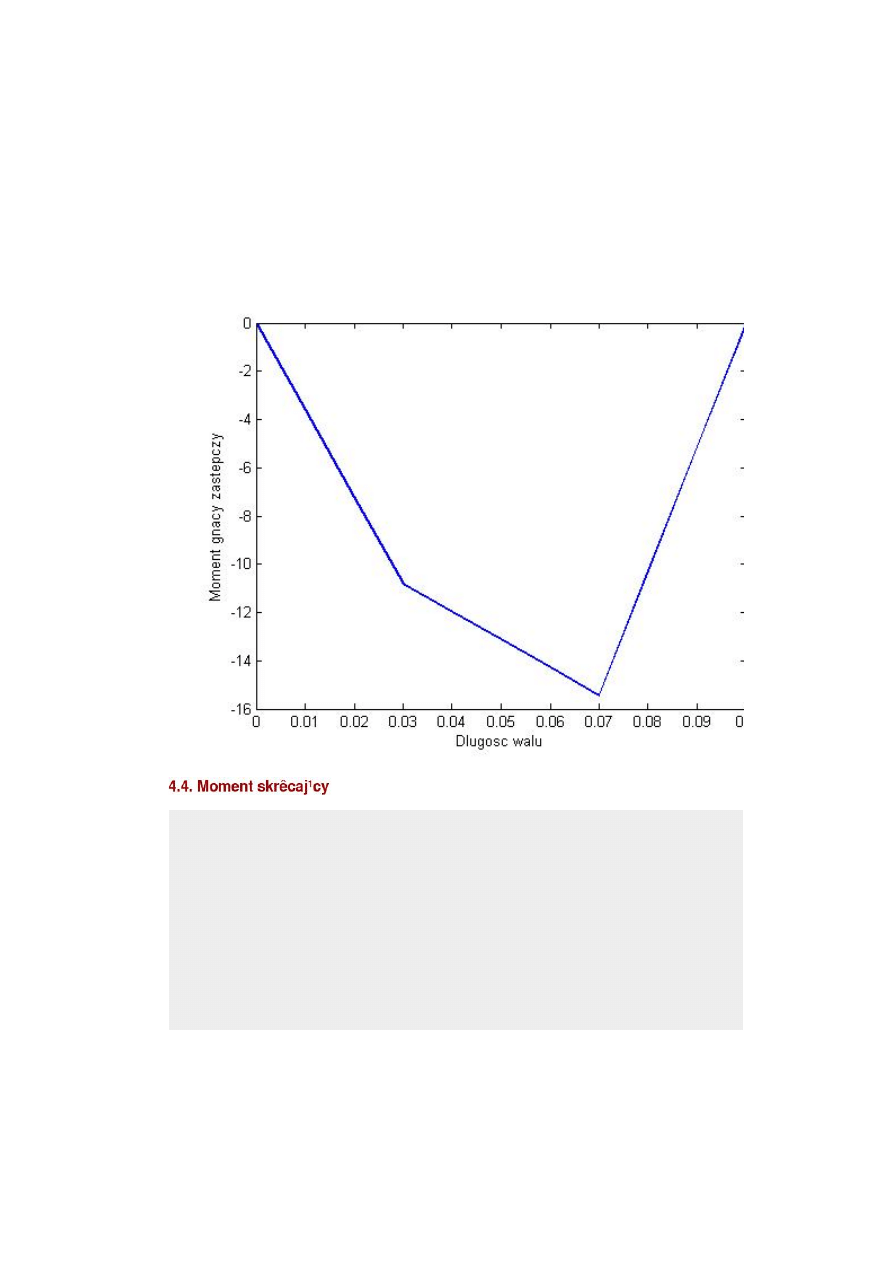
0 3.6045 7.2090 10.8135 10.8096 11.9931 13.2476

Columns 8 through 13

14.5550 15.9021 15.9021 10.6014 5.3007 0

M_s=M_2

ll=l;

for

(aa=1:length(l))

if

(l(aa)<0.03 || l(aa)>0.07)

ll(aa)=0;

else

ll(aa)=1;

end

M_ss(aa)=M_s*ll(aa);

end

M_s=M_ss;

M_s =

5.5092

5.5092

k_sj=85

k_so=45

k_go=80

k_sj =

85

k_so =

45

k_go =

80

%strona 177 osinski

M_s_prim=sqrt(3)/2*k_so/k_sj*M_s

M_s_prim =

Columns 1 through 7

0 0 0 2.5259 2.5259 2.5259 2.5259

Columns 8 through 13

2.5259 2.5259 2.5259 0 0 0

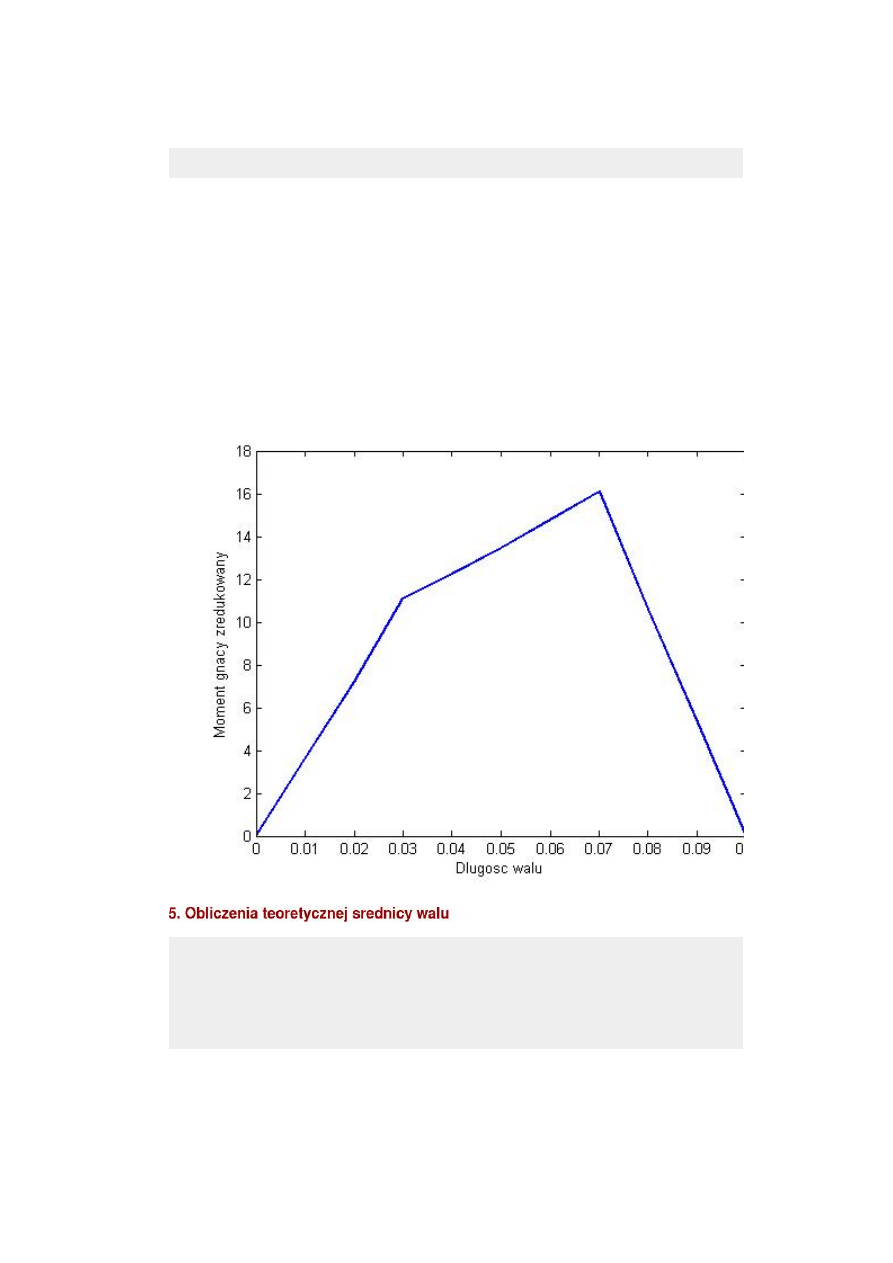
M_z=sqrt(Mg_w.^2+M_s_prim.^2)

figure(4)

plot(l,M_z,

'linewidth'

,2);

xlabel(

'Dlugosc walu'

)

ylabel(

'Moment gnacy zredukowany'

)

xlabel(

'Dlugosc walu'

)

ylabel(

'Moment gnacy zredukowany'

)

M_z =

Columns 1 through 7

0 3.6045 7.2090 11.1046 11.1008 12.2562 13.4863

Columns 8 through 13

14.7725 16.1014 16.1014 10.6014 5.3007 0

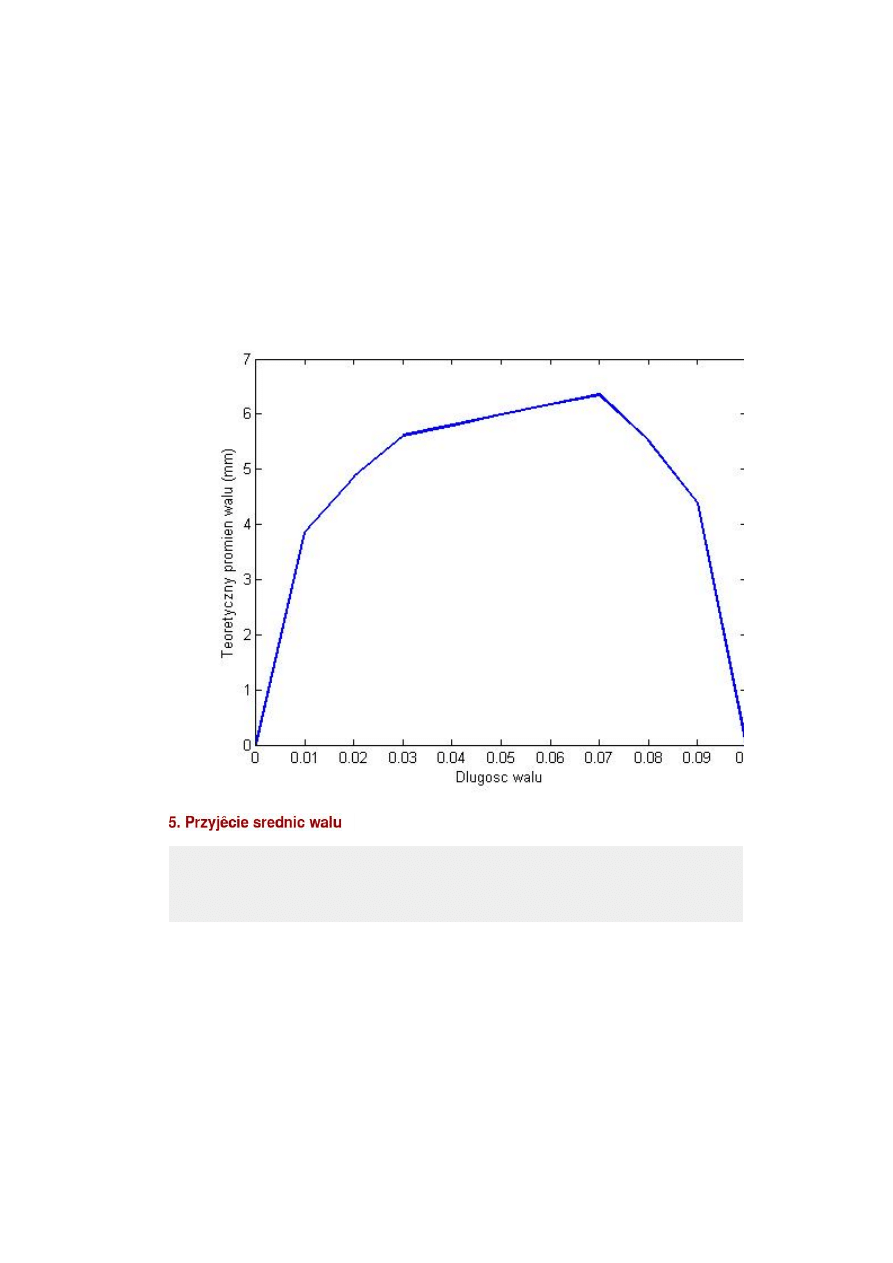
d_teor=(M_z*32/pi/(k_go*1e6)).^(1/3)

figure(6)

plot(l,d_teor/2*1e3,

'linewidth'

,2);

xlabel(

'Dlugosc walu'

)

ylabel(

'Teoretyczny promien walu (mm)'

)

d_teor =

Columns 1 through 7

Columns 1 through 7

0 0.0077 0.0097 0.0112 0.0112 0.0116 0.0120

Columns 8 through 13

0.0123 0.0127 0.0127 0.0111 0.0088 0

%Srednica walu pod kolem zebatym powiekszono o 20%

d_kolazebatego_2=d_teor(4)*1.2

d_kolazebatego_3=d_teor(10)*1.2

d_kolazebatego_2 =

0.0135

d_kolazebatego_3 =

0.0152

L_p=(1.6)*d_kolazebatego_2

% Grubosc wpustu

g=(0.25)*d_kolazebatego_2

% Srednica zewnetrzna piasty kola zebatego

Dp=d_kolazebatego_2+2*g

L_p =

0.0215

g =

0.0034

Dp =

0.0202

F_wpustu=2*M_2/d_kolazebatego_2

F_wpustu =

818.0882

b=4

h=4

b =

4

4

h =

4

p_dop=0.8*120*1e6;

Z_cj=360*1e6

x_z=2;

kcj=Z_cj/x_z

l_0=2*F_wpustu/(h*1e-3*p_dop)

Z_cj =

360000000

kcj =

180000000

l_0 =

0.0043

srednica_loz_lewego=d_kolazebatego_2/1.1

srednica_loz_lewego =

0.0122

srednica_loz_lewego=12

srednica_loz_praweg=d_kolazebatego_3/1.2

srednica_loz_lewego =

12

12

srednica_loz_praweg =

0.0127

srednica_loz_prawego=14

srednica_loz_prawego =

14

%rzadana trwalosc lozy

L_h=9600;

L=(L_h*n*60)/10^6

c_przez_p=(L)^(1/3)

R_A=sqrt(R_Ay^2+R_Az^2)

R_B=sqrt(R_Bz^2+R_Bz^2)

L =

1.4976e+003

c_przez_p =

11.4410

R_A =

360.4511

R_B =

727.1786

C_b=R_B*c_przez_p

C_b =

8.3197e+003

Co= 4.2*1e3

spr_loz=R_Bx/Co

Co =

4200

spr_loz =

-0.0051

R_m=650*1e6;

% Naprezenia dopuszczalne przy skrecaniu obustronnym

Z_so=0.25*R_m

Z_go=0.45*R_m

a=h*b/21e-6*(b-b/2)^2/d_kolazebatego_2/2

Wx=(pi*d_kolazebatego_2^3)/32

Wo=(pi*d_kolazebatego_2^3)/16

naprezenia_gnace=Mg_w(7)/Wx

naprezenia_tnace=M_s(7)/Wo

suma_sigma=sqrt(naprezenia_gnace^2+naprezenia_tnace^2)

if

suma_sigma>Z_so

disp(

'Zle obliczenia poopraw'

)

else

disp(

'Wszystko ok, dobrze dobrana srednica pod kolem zebatym'

)

disp(

'Nalezy przejsc do obliczania wspolczynnika bezpieczenstwa'

)

end

end

Z_so =

162500000

Z_go =

292500000

a =

1.1314e+008

Wx =

2.3986e-007

Wo =

4.7972e-007

naprezenia_gnace =

5.5231e+007

naprezenia_tnace =

1.1484e+007

suma_sigma =

5.6412e+007

Wszystko ok, dobrze dobrana srednica pod kolem zebatym

Nalezy przejsc do obliczania wspolczynnika bezpieczenstwa

X_zg=Z_go/naprezenia_gnace

X_zs=Z_so/naprezenia_tnace

X_zg =

5.2960

5.2960

X_zs =

14.1498

disp(

'Zaokraglenia w wpuscie przyjmniemy jako 0.2mm'

)

%wysokosc wpustu jest 2mm = h/2

% z tablic w mazanku strona 43, odczytujemy wspolczynnik 0.2/2

alfa_k=3.6

% Dla Rm=700Mpa oraz chropowatosci w wpuscie 1.25

beta_p=1.25;

% z wykresu 2.11 - mazanek

ni_k=0.55

%Z wykresu 2.13

epsilon=1.1

beta_k=1+ni_k*(alfa_k-1)

beta_bez=beta_k+beta_p-1

Zaokraglenia w wpuscie przyjmniemy jako 0.2mm

alfa_k =

3.6000

ni_k =

0.5500

epsilon =

1.1000

beta_k =

2.4300

beta_bez =

2.6800

delta_g=(epsilon/beta_bez)*X_zg

delta_s=(epsilon/beta_bez)*X_zs

delta_g =

2.1737

delta_s =

5.8078

disp(

'Rzeczywisty wspolczynnik bezpieczenstwa wyszedl '

)

delta=(delta_g*delta_s)/(sqrt(delta_g^2+delta_s^2))

disp(

'Jest to odpowiedni wspólczynnik dla obliczen zgrubnych'

)

Rzeczywisty wspolczynnik bezpieczenstwa wyszedl

delta =

2.0358

Jest to odpowiedni wspólczynnik dla obliczen zgrubnych