
1
Laboratorium z Hydrauliki i Hydrologii – Kierunek Budownictwo inż – sem. V
Politechnika Gdańska
Katedra Hydrotechniki
WILIŚ
Analiza przepływu wody przez przekrój mostowy (FM)
1. Cel ćwiczenia
Celem ćwiczenia jest rozpoznanie hydraulicznych warunków przepływu wody w kanale
laboratoryjnym, w którym może istnieć lokalne utrudnienie przepływu wody, spowodowane
obecnością filarów mostu.
Mosty należą do drogowych obiektów inżynierskich, których projektowanie leży w gestii
inżynierów budownictwa. Niezbędne elementy projektu zawarte są m.in. w Rozporządzeniu
Ministra Transportu i Gospodarki Morskiej z 30 maja 2000 roku. w sprawie warunków
technicznych, jakim powinny odpowiadać drogowe obiekty inżynierskie i ich usytuowanie –
Dz.U. Nr 63 poz. 735. We wspomnianym rozporządzeniu, podane są sposoby uwzględniania
zagadnień hydraulicznych w projektowaniu obiektów inżynierskich, jednakże nie zawsze
odzwierciedlają one w pełni rzeczywisty przebieg zjawisk towarzyszących przepływom przez
tego typu obiekty.
2. Informacje ogólne
Wymienione wcześniej Rozporządzenie Ministra Transportu i Gospodarki Morskiej z dnia 30
maja 2000 r. zwraca uwagę na konieczność zapewnienia bezpieczeństwa obiektów
inżynierskich, z uwagi na możliwość wystąpienia zjawisk ekstremalnych, w tym m.in.
powodzi.
Rozporządzenie przewiduje, że usytuowanie mostu i trasy dojazdowej nie powinno
spowodować istotnych zmian koryta cieku oraz warunków przepływu wód, jeśli nie wynika to
z konieczności regulacji koryta cieku. Tymczasem w rzeczywistości każda inwestycja
drogowa lokalizowana w korycie głównym lub terenach zalewowych cieku istotnie zmienia
warunki hydrauliczne wody płynącej. Omówienie i rozszerzenie rozporządzenia znaleźć
można na przykład w pracy Madaja i Wołowickiego pt. „Podstawy projektowania budowli
mostowych” (2007).
2
W ćwiczeniu laboratoryjnym szczególną uwagę należy zwrócić na porównanie
hydraulicznych warunków przepływu wody w korycie bez filarów oraz opływającej filary
mostu w kanale laboratoryjnym.
Przepływ wody w kanale otwartym opisywany jest układem równań złożonym z równania
ciągłości oraz równania dynamicznego.
2.1 Równanie ciągłości
Równanie ciągłości w ruchu ustalonym dla strumienia bez dopływu bocznego zapisać można
następująco:
const
A
v
Q
=
⋅
=
(1)
Q oznacza natężenie przepływu wody w kanale (wydatek), który podawany najczęściej jest w
jednostce m
3
/s, A oznacza pole powierzchni przekroju czynnego kanału w m
2
lub cm
2
zaś v
oznacza prędkość średnią w przekroju poprzecznym kanału (wyrażoną w m/s lub cm/s).
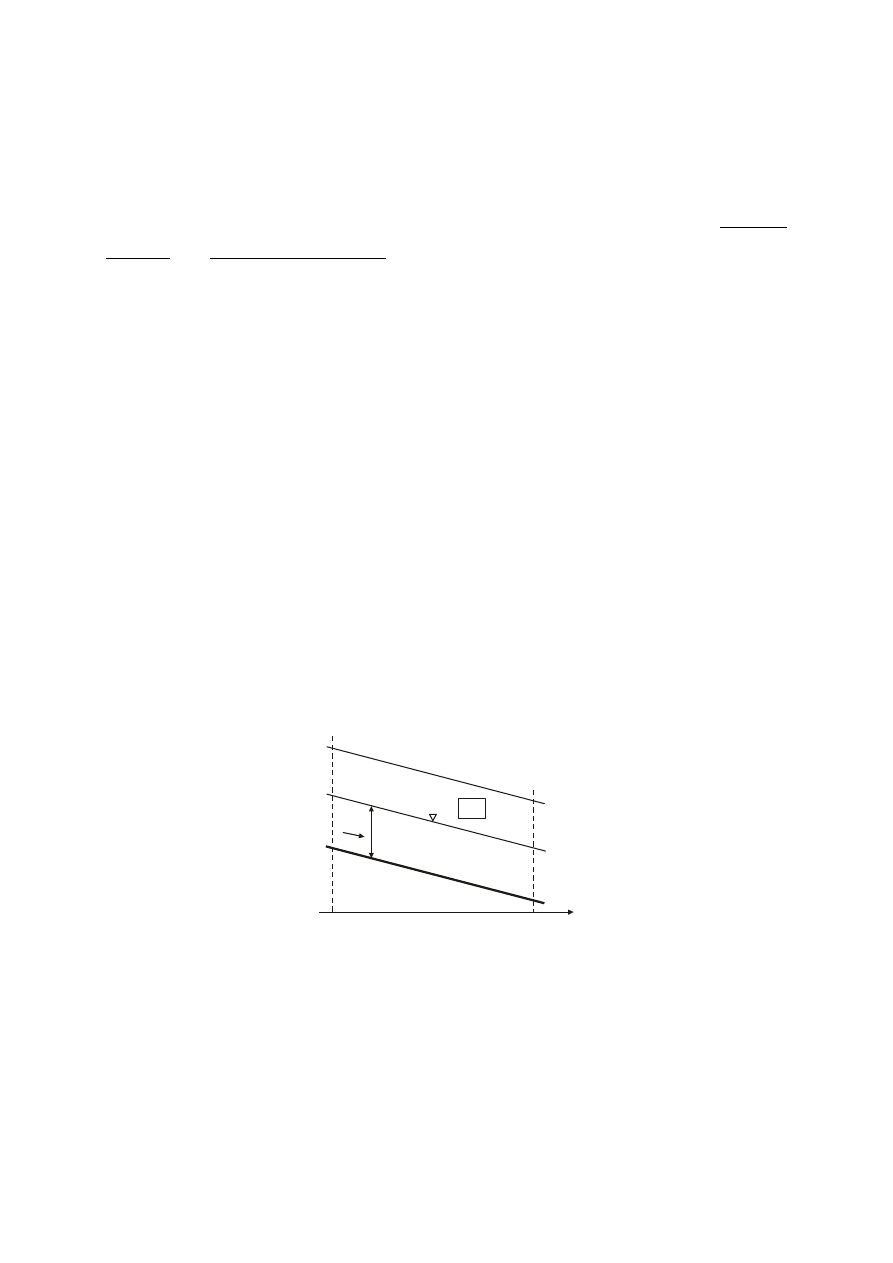
W obliczeniach prędkości średniej w kanałach otwartych przyjmuje się często założenie, że
przepływ jest ustalony i jednostajny. Przepływ ustalony oznacza niezmienność parametrów
opisujących ruch wody w czasie. Przepływ jednostajny oznacza, że w każdym przekroju
poprzecznym kanału otwartego stałe są wartości napełnienia kanału (h), natężenia przepływu
(Q) oraz prędkości średniej (v) (rys.1).
i - spad
ek dna
LE
LC
I - spad
ek hydra
uliczny
v
h
i=I
x
1
2
rys. 1. Linia energii i linia ciśnienia w warunkach ruchu ustalonego jednostajnego, LE-linia energii, LC-linia
ciśnienia
W rzeczywistości ruch ustalony jednostajny występuje niezmiernie rzadko. Prawie zawsze w
przypadku ruchu ustalonego w kanałach naturalnych występuje ruch niejednostajny, tzn.
parametry przepływu są zmienne w kolejnych przekrojach poprzecznych wzdłuż kanału.
3
Do najczęstszych metod oszacowania prędkości średniej w kanałach otwartych służy formuła
Manninga. Dokładniejsze wartości prędkości średniej można oszacować na podstawie
pomiarów prędkości lokalnych (miejscowych) w różnych punktach przekroju poprzecznego.
2.1.1 Wyznaczenie prędkości średniej z formuły Manninga
Przy założeniu ruchu ustalonego jednostajnego w kanale otwartym, prędkość średnią wody
wyznaczyć można z formuły Manninga:
2
1
3
2
1
I
R
n
v
=
(2)
W równaniu powyższym n oznacza współczynnik szorstkości, którego wartości zestawione są
w tabeli (patrz: przydatne informacje). I jest spadkiem hydraulicznym, który w warunkach
ruchu ustalonego jednostajnego jest równy spadkowi zwierciadła wody oraz spadkowi dna i.
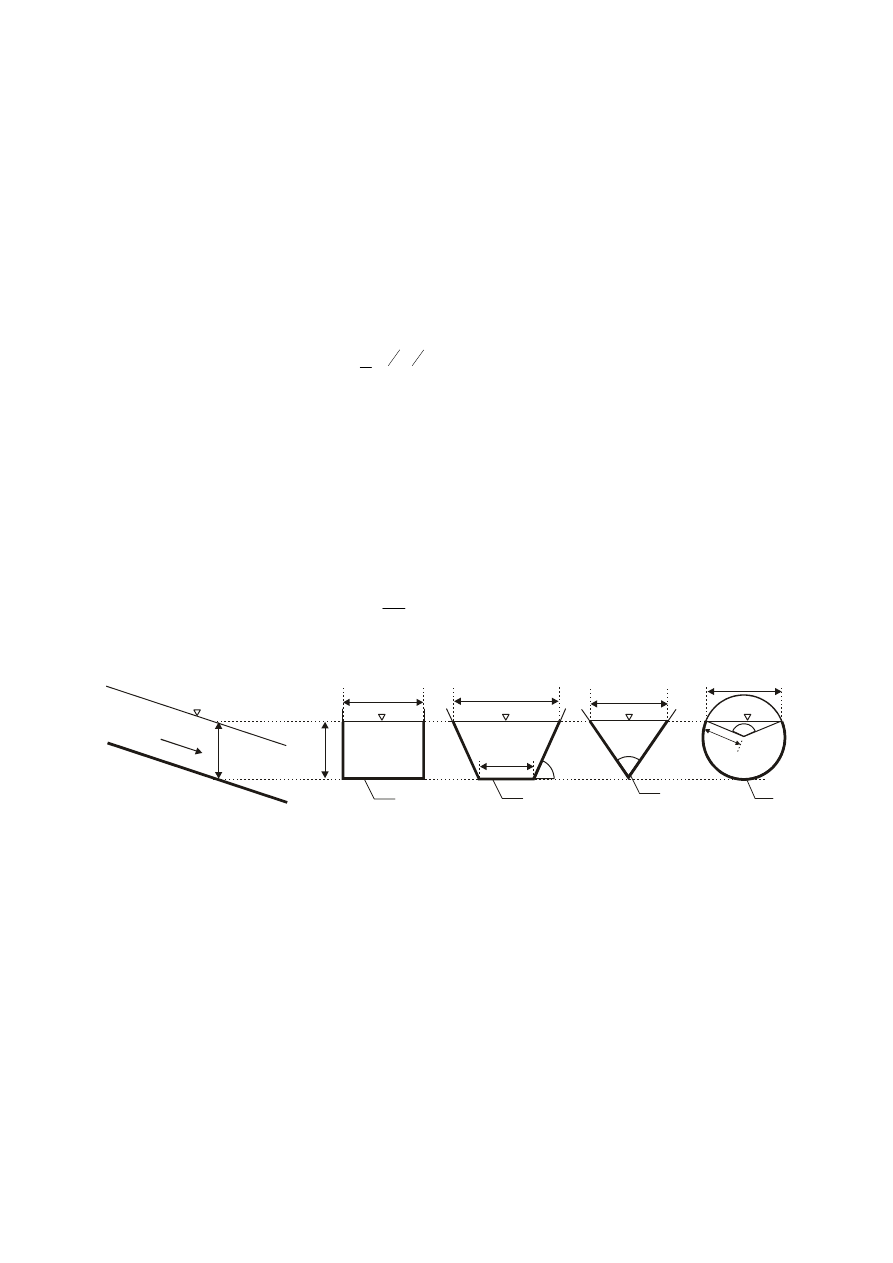
Występujący w równaniu Manninga promień hydrauliczny R wyznaczamy na podstawie
znajomości powierzchni pola przekroju czynnego A oraz obwodu zwilżonego Oz (rys.2),
zgodnie z relacją:
Oz
A
R
=
(3)
h
v
A
A
A
O
z
O
z
O
z
B
B
A
O
z
B
h
b
α
α
1
:m
B
ϕ
r
Rys. 2. Parametry kanału otwartego A – pole powierzchni przekroju czynnego, B – szerokość kanału na
wysokości zwierciadła wody, b – szerokość dna, Oz – obwód zwilżony, h – głębokość wody
2.1.2 Wyznaczenie prędkości średniej i natężenia przepływu metodami
pośrednimi
Natężenie przepływu Q wody można określić wykorzystując metody pośrednie (np.
arytmetyczna, Harlachera, Culmanna). Podstawą obliczeń jest pomiar prędkości lokalnych w
wybranych punktach przekroju poprzecznego rozmieszczonych w tzw. pionach pomiarowych
(rys. 3). Prędkość lokalną pomierzyć można wykorzystując młynek hydrometryczny lub rurkę
pomiarową (rurkę Pitota, rurkę Prandla).
4
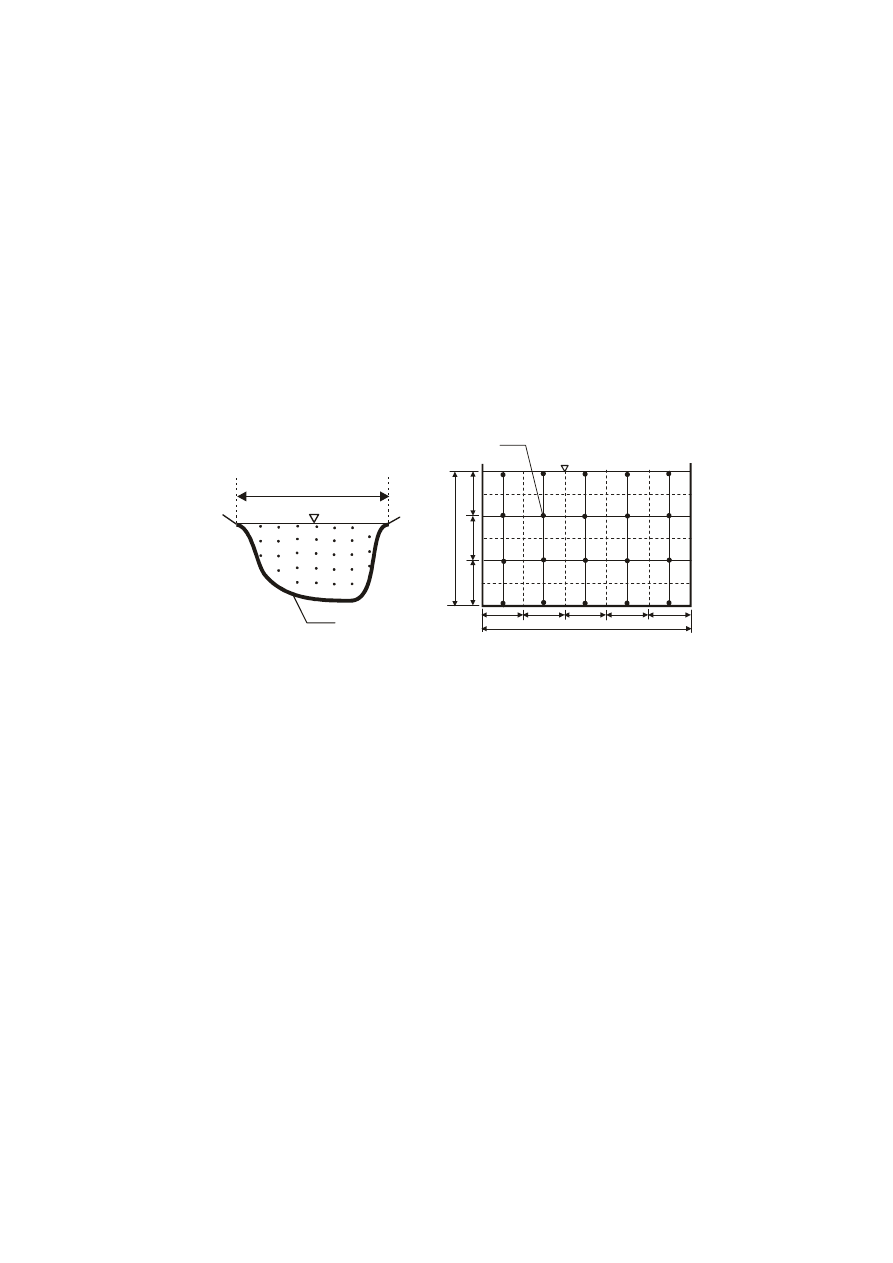
Piony pomiarowe w naturalnym cieku oddalone są od siebie o stałą wartość uzależnioną od
szerokości przekroju poprzecznego cieku. W prostokątnym kanale laboratoryjnym, w
zależności od przyjętej liczby pionów pomiarowych X, dwa sąsiednie piony oddalone są od
siebie o odległość równą x = B/X, zaś piony skrajne oddalone są o odległość równą x/2 od
ś
cianek kanału (rys. 3b).
W każdym pionie pomiarowym liczba punktów pomiarowych zależy od głębokości wody w
tym pionie (rys. 3a), bowiem odległość pomiędzy kolejnymi punktami powinna być stała
(określana na podstawie wyników sondowania). W prostokątnym kanale laboratoryjnym
skrajne punkty pomiarowe w danym pionie umieszczone są przy dnie i przy zwierciadle
swobodnym wody (rys. 3b).
A
O
z
B
I
y
v
i
III
II
V
IV
y
y
h
x
x
x
x
B
x
a)
b)
Rys. 3. Rozkład punktów pomiaru prędkości lokalnych w przekroju poprzecznym : a) naturalnego cieku
b) kanału prostokątnego.
2.1.2.1 Pomiar prędkości lokalnej za pomocą młynka hydrometrycznego
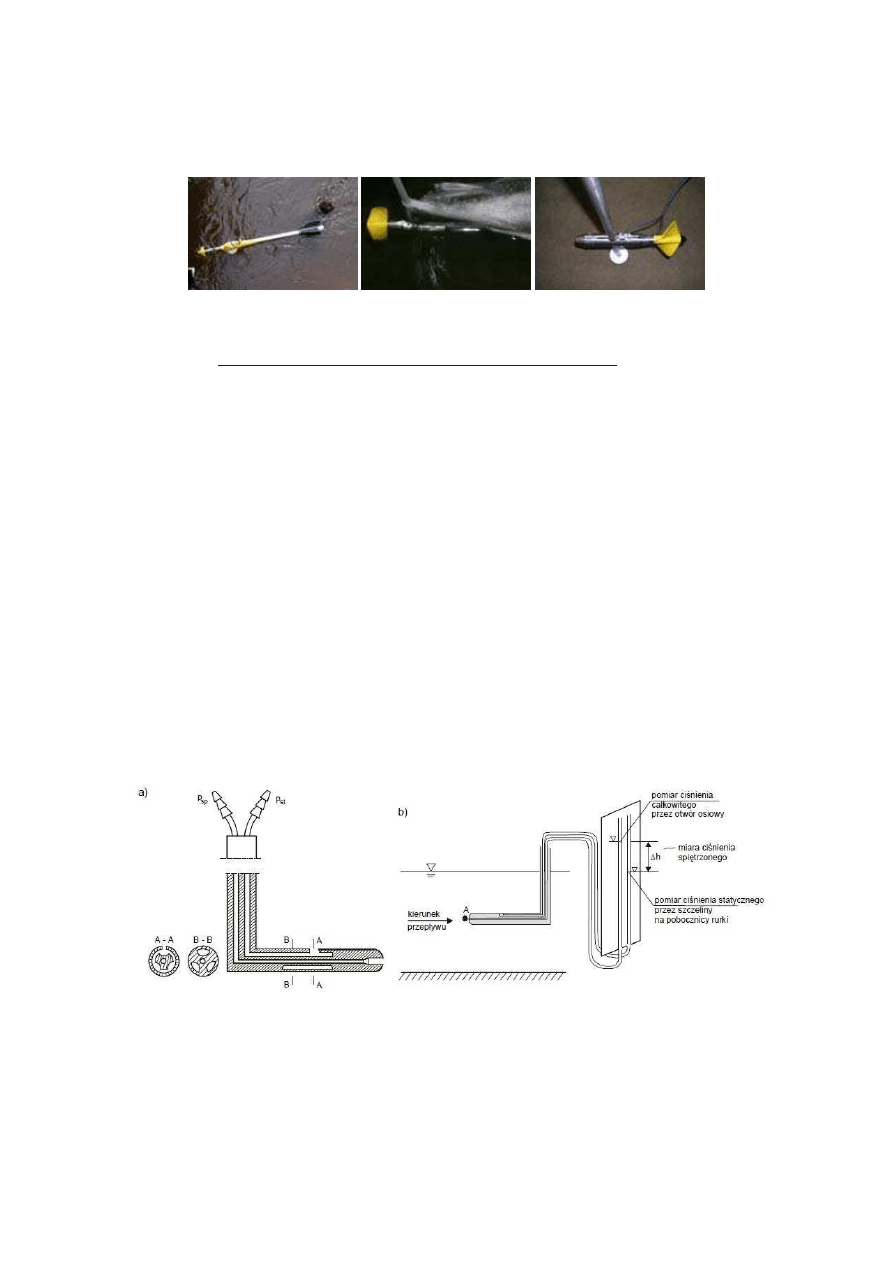
W pomiarach za pomocą młynków hydrometrycznych wykorzystuje się wpływ energii
kinetycznej wody na prędkość obrotową śmigła młynka (rys.4). Obroty młynka są zliczane w
określonym czasie (najczęściej 50 lub 100 sekund). Prędkość wody w punkcie przyłożenia osi
młynka v
L
określa się wykorzystując równanie młynka zwane również charakterystyką
młynka:
m
L
n
v
⋅
+
=
β
α
(4)
W powyższym wzorze n
m
oznacza najczęściej prędkość obrotową wirnika, czyli stosunek
ilości obrotów wirnika młynka do czasu rejestracji.
α, β
są stałymi charakterystycznymi dla
każdego młynka hydrometrycznego. Stałe młynka są każdorazowo określane na podstawie
5
cechowania (tarowania) przyrządu pomiarowego w atestowanym laboratorium Głównego
Urzędu Miar i można je znaleźć w świadectwie tarowania młynka.
Rys. 4. Młynek hydrometryczny na zdjęciach IMGW a) młynek opuszczany na lince, b) młynek pracujący w
wodzie, c) wygląd młynka zamontowanego na żerdzi pomiarowej. (źródło:
www.imgw.pl/internet/zz/wiedza/ogolna/_pom_prog/mlynek.html
09/2009)
2.1.2.2 Pomiar prędkości lokalnej za pomocą rurki Prandla
Rurka Prandla (rys. 5) jest wykorzystywana do pomiaru prędkości lokalnej w kanałach
laboratoryjnych, w których woda jest pozbawiona zawiesin. Wewnątrz rurki umieszczone są
dwa kanaliki. Pierwszy z nich połączony jest z boczną ścianką (pobocznicą) rurki i mierzy
ciśnienie statyczne wody w rurce, którego wysokość jest równa wysokości warstwy wody
płynącej ponad korpusem rurki. Drugi kanalik umieszczony jest wzdłuż osi rurki i mierzy
całkowite ciśnienie (sumę ciśnienia statycznego i dynamicznego wody płynącej). Podczas
pomiaru wykorzystywane jest więc zjawisko zamiany energii kinetycznej płynącej cieczy na
energię potencjalną w postaci dodatkowego spiętrzenia wody w rurce.
Pomiar należy wykonywać w ten sposób, aby oś przyrządu była skierowana równolegle do
kierunku napływającej wody (rys. 5).
Rys. 5. Schemat rurki Prandla a) schemat budowy, b) ustawienie w trakcie pomiaru (źródło: Laboratorium z
mechaniki płynów i hydrauliki pod red. K. Weinerowskiej)
Prędkość lokalną wody w punkcie umieszczenia rurki Prandla wyznacza się ze wzoru:
6
h
g
v
L
∆
=
2
(5)
gdzie
∆
h jest różnicą wysokości ciśnień w kanalikach rurki Prandla.
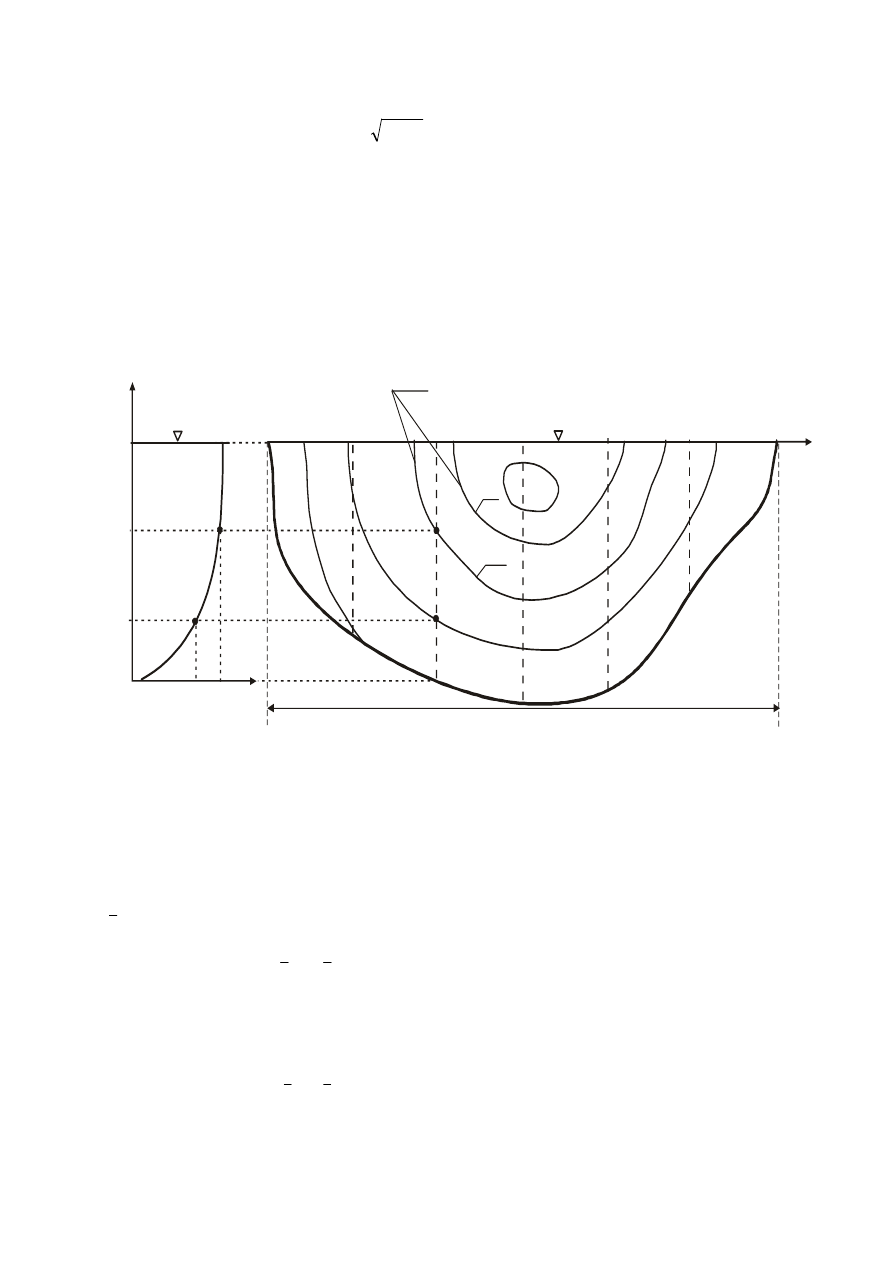
2.1.2.3 Wyznaczenie natężenia przepływu metodą Culmanna
Natężenie przepływu wody Q w przekroju poprzecznym kanału można wyznaczyć
wykorzystując metodę Culmanna. Na podstawie lokalnych wartości prędkości należy
wyznaczyć linie jednakowych prędkości zwane izotachami (rys. 6).
izotachy
H
[m]
∆Α
i
v
i
v
i+1
I
0.8
B
x
III
II
IV
V
0.9
1.0
0.7
1.1
0.8
0.9
0.9
0.8
0.8
0.8
1.0
V
V
[m/s]
0.8 0.9
1.0
0
1.3
0.5
Rys. 6. Izotachy prędkości w przekroju poprzecznym
Pomiędzy sąsiednimi izotachami prędkość przepływu wody zawiera się w przedziale
pomiędzy prędkościami odpowiadającymi wartościom izotach. W celu wyznaczenia natężenia
przepływu dla obszaru pomiędzy izotachami wprowadza się średnią prędkość obliczeniową
o
v
równą średniej arytmetycznej z wartości izotach ograniczających rozpatrywany obszar.
)
(
5
,
0
1
1
,
+
+
+
=
=
i
i
i
i
oi
v
v
v
v
(6)
W elemencie, w którym występują największe lokalne prędkości przepływu v
max
prędkość
obliczeniowa wyznaczana jest następująco:
)
(
5
,
0
max
,
mav
i
i
oi
v
v
v
v
+
=
=
(7)
7
natomiast w elemencie, w którym występują najmniejsze lokalne prędkości przepływu v
min
według wzoru:
i
i
oi
v
v
v
⋅
=
=
5
,
0
min
,
(8)
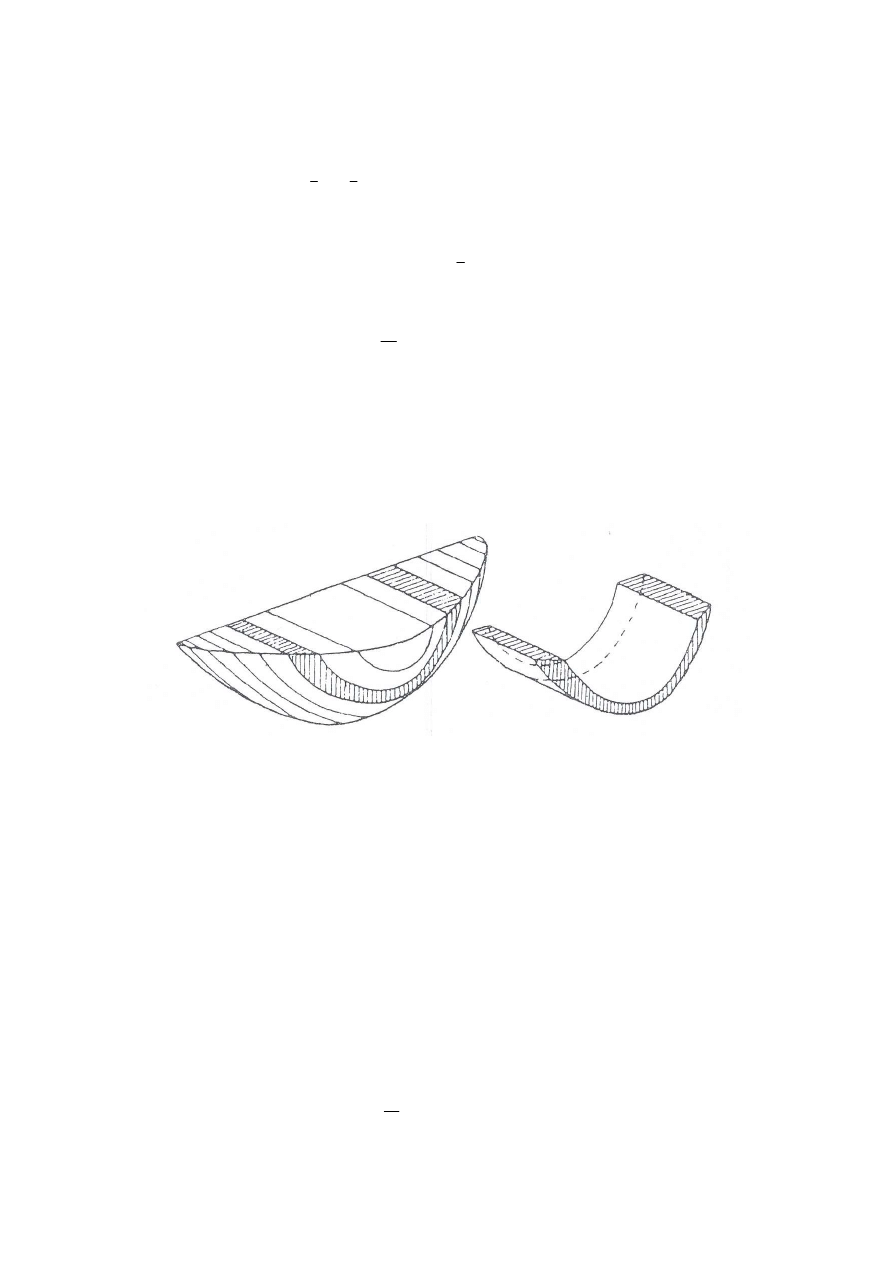
Natężenie przepływu z elementarnego obszaru przekroju poprzecznego A
i
, któremu
przypisuje się średnią prędkość obliczeniową
oi
v
graficznie stanowi elementarną objętość
natężenia przepływu (rys.7), którą można oznaczyć jako
∆
Q
i
.
i
oi
i
A
v
Q
⋅
=
∆
(9)
Całkowite natężenie przepływu stanowi suma natężeń przepływu z elementarnych obszarów
przekroju poprzecznego:
∑
=
∆
=
N
i
i
Q
Q
1
(10)
Rys. 7. Podział bryły przepływu w schemacie Culmanna na elementarne objętości natężenia przepływu
(Byczkowski A. Hydrologia)
Prędkość średnią w przekroju poprzecznym kanału otwartego wyznaczyć można z równania
ciągłości (1). Sposób wyznaczenia przedstawiono poniżej.
2.1.3 Wyznaczenie prędkości średniej z równania ciągłości
Znając natężenie przepływu Q oraz pole przekroju poprzecznego kanału otwartego A
prędkość średnią v w przekroju poprzecznym obliczyć można bezpośrednio z równania
ciągłości:
A
Q
v
=
(11)

8
W kanale laboratoryjnym o przekroju prostokątnym, pole przekroju poprzecznego wyznacza
się na podstawie znajomości jego szerokości B (zmierzonej w trakcie wykonywania
ć
wiczenia) oraz głębokości wody w przekroju poprzecznym h (A = B h). Średnia głębokość
wody mierzona jest w osi kanału na podstawie pomiaru rzędnych zwierciadła wody i dna.
W pomiarach hydrometrycznych przekrojów naturalnych prędkość średnią v wyznaczyć
można na podstawie natężenia przepływu obliczonego metodami pośrednimi Q oraz
znajomości pola przekroju poprzecznego A (równanie 11). Pole przekroju poprzecznego A
otrzymuje się na podstawie sondowania dna przekroju poprzecznego. Sondowanie wykonuje
się cechowanymi żerdziami w określonych odstępach (najczęściej co 0,5 metra, 1 metr lub 2
metry w zależności od szerokości cieku) mierzy się względną różnicę rzędnych dna i
zwierciadła wody.
Do wyznaczania parametrów przekroju poprzecznego używane są również echosondy
pomiarowe wykorzystujące sygnał ultradźwiękowy.
2.1.4 Określenie rzeczywistego natężenia przepływu za pomocą urządzeń
kontrolnych
W laboratorium możliwe jest dokonanie dodatkowego pomiaru rzeczywistego natężenia
przepływu za pomocą urządzeń kontrolnych zamontowanych na stanowiskach pomiarowych.
Woda doprowadzona do kanału przepływa uprzednio przez specjalnie wytarowane przelewy
o ostrej krawędzi. Każdy przelew ma swoją indywidualną charakterystykę natężenia
przepływu Q w zależności od poziomu jego wypełnienia. Sposób obliczania natężenia
przepływu w przelewie o ostrej krawędzi znaleźć można w części: przydatne informacje.
Znajomość wartości rzeczywistego natężenia przepływu z urządzenia kontrolnego umożliwia
ocenę dokładności stosowanych metod obliczeniowych. W warunkach rzeczywistych w
większości przypadków brak jest możliwości pomiarów kontrolnych i tym samym weryfikacji
przeprowadzonych obliczeń.
2.2 Równanie dynamiczne
Równanie dynamiczne jest reprezentowane przez równanie Bernoulliego bilansujące energię
mechaniczną na długości strumienia kanału otwartego. Przy bilansowaniu energii rozpatruje
się dwa przekroje oddalone od siebie o odległość L. W każdym z przekrojów określa się
wysokość energii mechanicznej będącej sumą: wysokości energii potencjalnej (składającą się
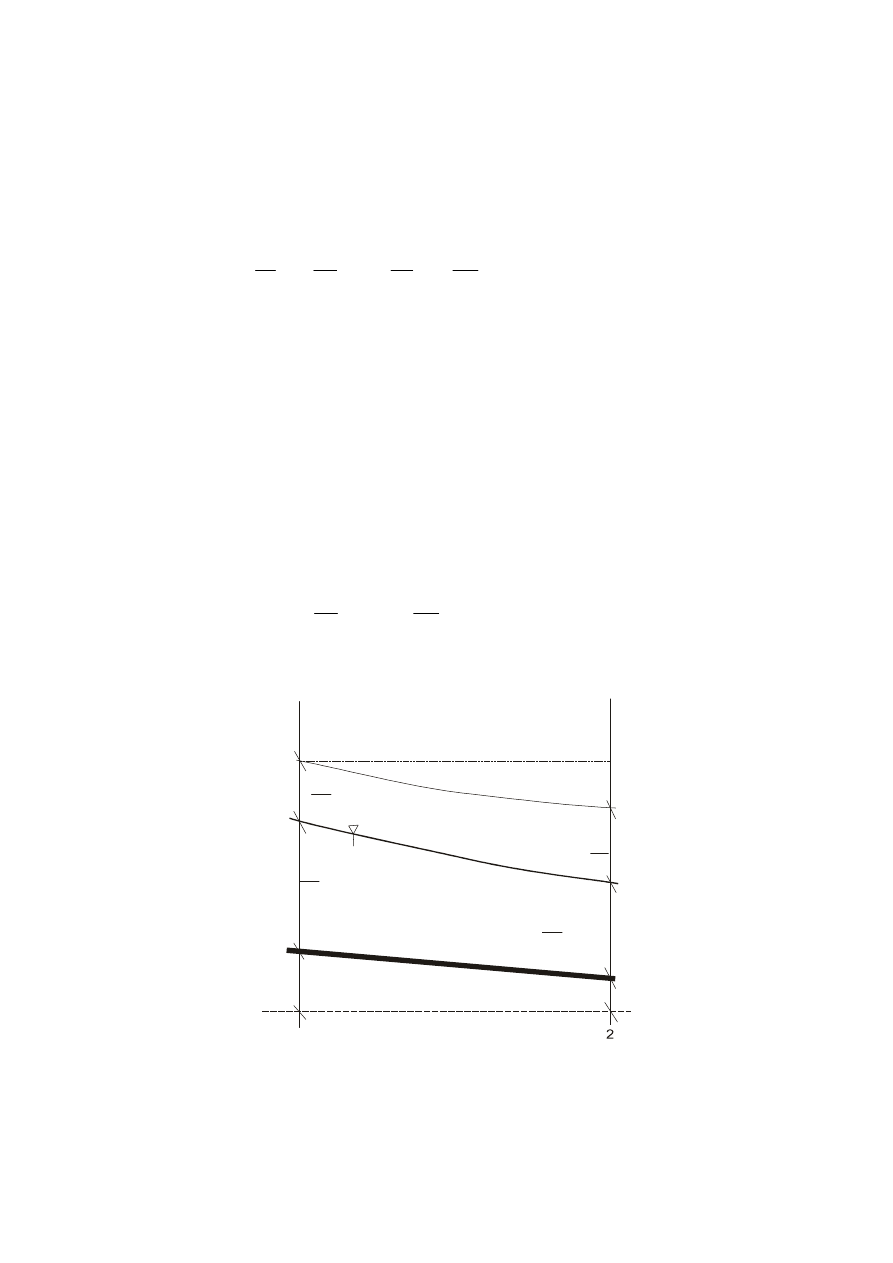
9
z wysokości położenia i wysokości ciśnienia), oraz wysokości energii kinetycznej (wysokości
prędkości) (rys.8). Dla przekroju 1 określa się zatem odpowiednio wysokość położenia z
1
,
wysokość ciśnienia p
1
/
γ
, oraz wysokość prędkości
α
v
1
/2g. Analogicznie wysokości te
wyznaczyć można dla przekroju 2. Równanie Bernoulliego można zapisać w postaci:
2
1
2
2
2
2
2
2
1
1
1
1
2
2
−
+
+
+
=
+
+
str
h
g
v
p
z
g
v
p
z
α
γ
α
γ
(12)
Występujący w równaniu współczynnik
α
zwanym jest współczynnikiem de Saint-Venanta.
Zakres jego wartości w kanale laboratoryjnym rzadko przekracza wartość 1,15. W
obliczeniach można przyjmować wartość
α
= 1,1. Pomiędzy przekrojami 1-2 występują straty
energii mechanicznej h
str1-2
.
W przypadku kanału o poziomym dnie, gdzie poziom porównawczy można przyjąć na linii
dna, wysokości położenia z
1
i z
2
będą równe 0, zaś wysokości ciśnienia, określone zgodnie z
hydrostatycznym rozkładem ciśnień, będą równe głębokości wody h
1
i h
2
. Wobec
powyższego równanie Bernoulliego można zapisać w postaci:
2
1
2
2
2
2
2
1
1
1
2
2
−
+
+
=
+
str
h
g
v
h
g
v
h
α
α
(13)
poziom porównawczy
dno kanału
linia ci
ś
nienia (zw. w
ody)
linia energii
rzeczywiste
j
z
2
z
1
p
1
2g
h
str 1-2
γ
p
2
γ
v
1
2
α
1
2g
v
2
2
α
2
E=const
L
1
= h
1
= h
2
Rys. 8. Graficzna interpretacja równania Bernoulliego

10
2.3 Zależność wartości energii od napełnienia kanału
W ruchu ustalonym, niejednostajnym, w każdym przekroju kanału zmienia się wartość energii
potencjalnej i kinetycznej. Całkowita energia mechaniczna właściwa (liczona w przekroju
względem przyjętego poziomu odniesienia) jest sumą głębokości oraz wysokości prędkości
wody.
g
v
h
E
2
2
α
+
=
(14)
Po podstawieniu równania ciągłości (
A
Q
v
=
) wzór na wartość jej energii przyjmie postać:
2
2
2gA
Q
h
E
α
+
=
(15)
Dla kanału o przekroju prostokątnym pole przekroju czynnego stanowi iloczyn stałej
szerokości kanału B, oraz głębokości wody h. Zatem całkowita energia mechaniczna
właściwa w kanale prostokątnym w warunkach ruchu ustalonego jest tylko funkcją
napełnienia kanału.
2
2
2
2
B
gh
Q
h
E
α
+
=
(16)
Pierwszy człon (E
p
=h) oznacza udział wysokości energii potencjalnej, zaś drugi
(
2
2
2
2
B
gh
Q
E
k
α
=
) udział wysokości energii kinetycznej (rys.9).
E
h
ruch
nadkrytyczny)
spokojny
(
h
kr
E
min
E
c
E
p
E
k
ruch
krytyczny)
rw
ą
cy
(pod
Rys. 9. Wykres całkowitej energii mechanicznej właściwej E
c
(h) w kanale prostokątnym
Przy ustalonym przepływie istnieje pewna głębokość wody, dla której całkowita energia
mechaniczna właściwa osiąga minimum. Głębokość ta nazywana jest głębokością krytyczną
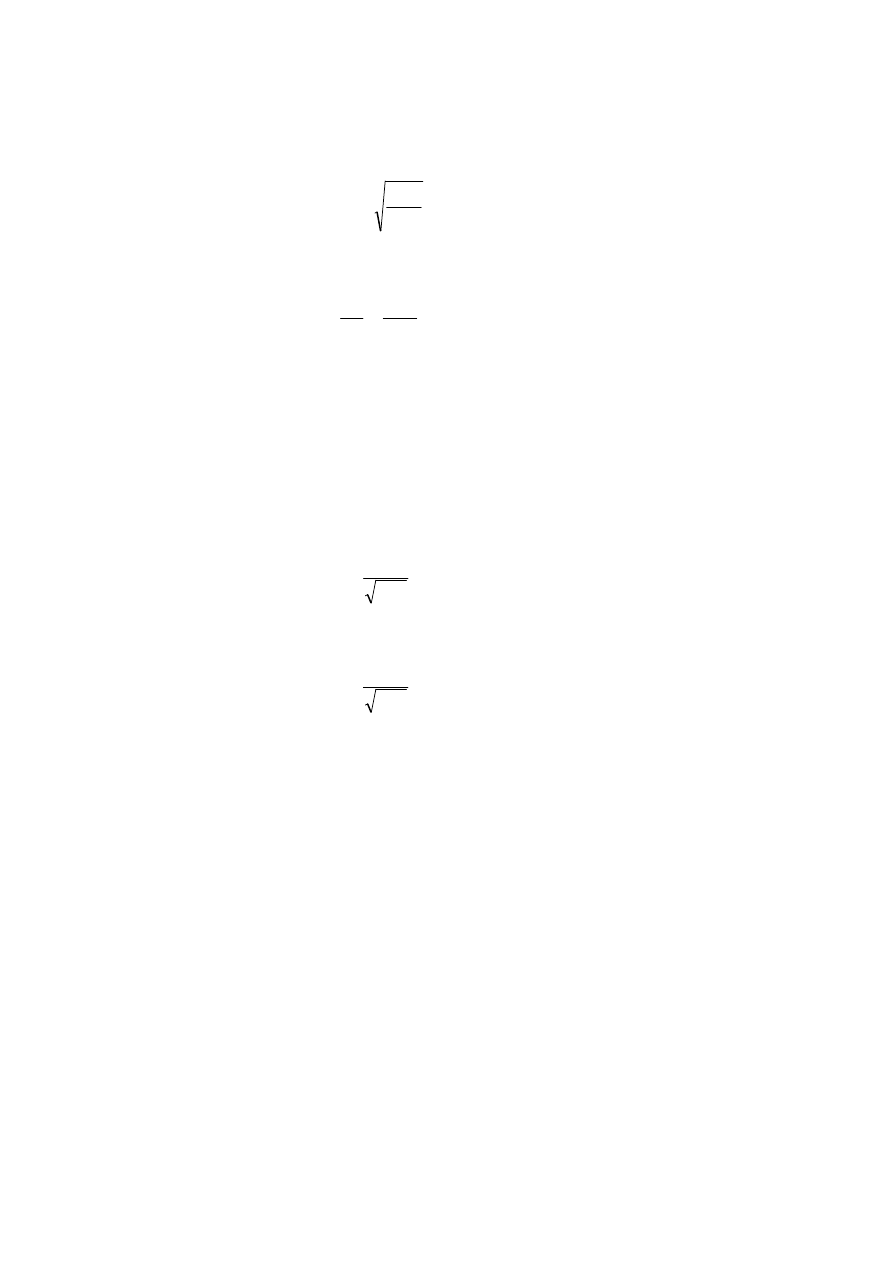
11
h
kr
. Głębokość krytyczną wyznaczamy znajdując minimum funkcji E
c
(h). Dla kanału
prostokątnego (B=const) głębokość krytyczna jest równa:
3
2
2
gB
Q
h
kr
α
=
(17)
W warunkach ruchu krytycznego wykorzystać można ogólne równanie:
g
aQ
B
A
2
3
=
(18)
Głębokość krytyczna jest bardzo ważną wielkością charakteryzującą hydrauliczne warunki
przepływu. Jeżeli rzeczywista głębokość wody jest mniejsza od głębokości krytycznej
(h<h
kr
), w kanale panują warunki ruchu podkrytycznego (rwącego). Jeżeli rzeczywista
głębokość wody jest większa od głębokości krytycznej (h>h
kr
), w kanale panują warunki
ruchu nadkrytycznego (spokojnego). Kryterium ruchu określa także bezwymiarowa wartość
liczby Froude’a: W ruchu nadkrytycznym (spokojnym):
1
<
=
sr
gh
v
Fr
(19)
zaś w ruchu podkrytycznym (rwącym):
1
>
=
sr
gh
v
Fr
(20)
Występująca w równaniach 19 i 20 średnia głębokość wody h
sr
w przekroju poprzecznym
koryta obliczana jest na podstawie ilorazu pola przekroju poprzecznego A oraz szerokości
zwierciadła wody B (h
sr
= A/B).
W większości przypadków rzek nizinnych w kanałach otwartych panują warunki ruchu
spokojnego. W rejonie wybudowanego obiektu mostowego warunki przepływu są
uzależnione od wielkości natężenia przepływu wody w kanale oraz geometrii przekroju. Z
reguły woda przepływa przez przekrój mostowy ruchem spokojnym. Jednakże w pewnych
warunkach może wystąpić ruch rwący (h
kr
> h). Na przykład w przewężeniu przekroju
następuje lokalny wzrost prędkości i rośnie wartość głębokości krytycznej h
kr
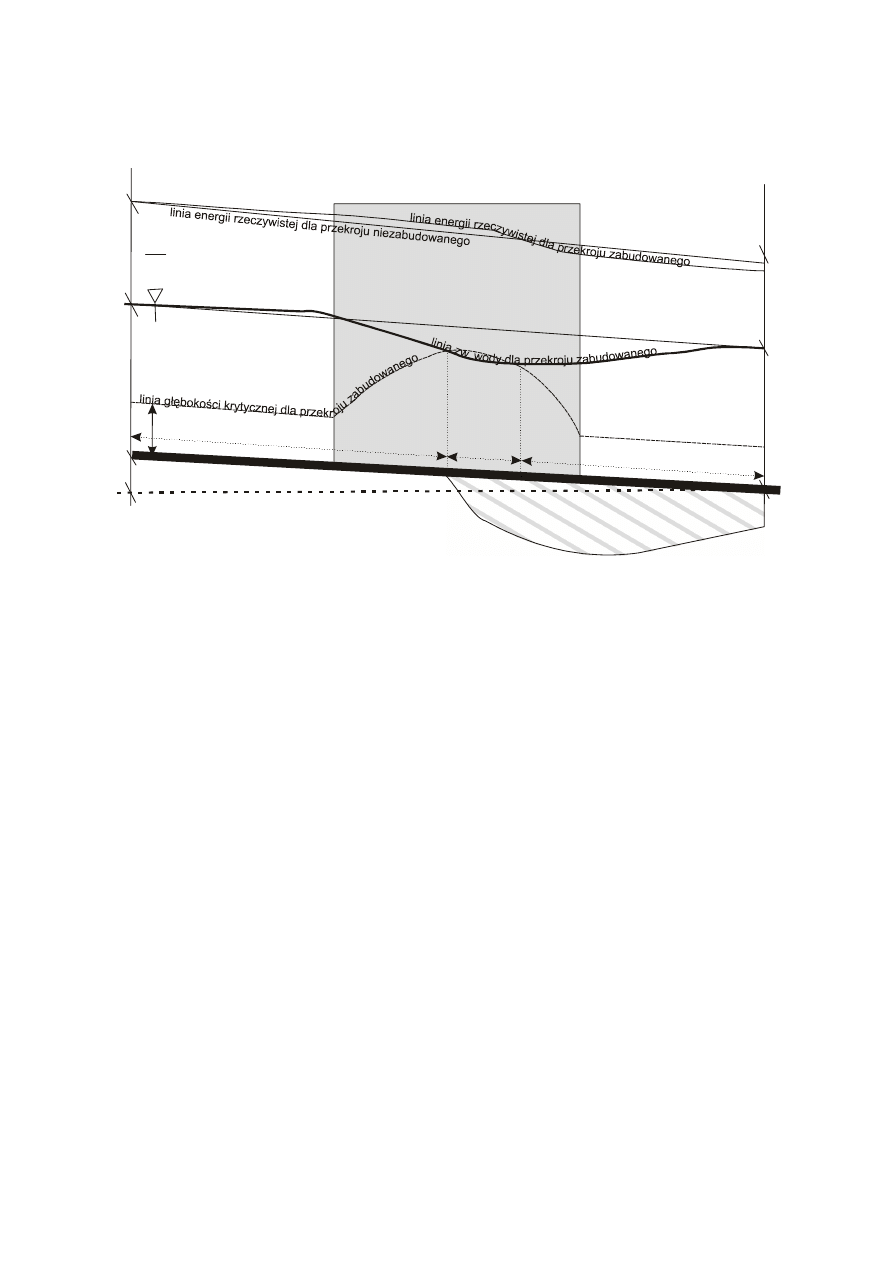
(rys. 10).
W czasie przepływu wody przez profil mostowy, w sąsiedztwie filarów i poniżej samego
przekroju może pojawić się erozja denna powodująca dodatkowy transport materiału dna.
Dlatego też przy obliczeniach hydraulicznych rzeczywistych konstrukcji mostowych należy
12
każdorazowo przeanalizować i określić możliwe pogłębienie koryta w przekroju mostowym
oraz rozmycia lokalne przy filarach mostu.
poziom porównawczy
h
2g
v
2
α
linia zw. wody dla przekroju niez
abudowanego
filar mostu
strefa ruchu spokojnego
dno kanału
L
z=iL
strefa potencjalnego
rozmywania dna
h
kr
strefa ruchu spokojnego
s
tr
e
fa
r
u
c
h
u
r
w
ą
c
e
g
o
Rys. 10. Ogólne warunki przepływu w kanale otwartym zabudowanym przekrojem mostowym dla ruchu
spokojnego
3. Schemat stanowiska pomiarowego
Stanowisko do wykonania ćwiczenia zlokalizowane jest w kanale laboratoryjnym, w którym
woda przepływa w układzie zamkniętym. Zasilanie kanału odbywa się poprzez stanowisko
pomp czerpiących wodę z magazynowego zbiornika wody, zlokalizowanych w części
piwnicznej hali „Hydro”. Woda bezpośrednio do kanału dostaje się poprzez dwie skrzynie
pomiarowe zakończone przelewami o ostrej krawędzi i przekroju kołowym. Po przejściu
przez kanał laboratoryjny woda powraca do zbiornika magazynowego.
Dno kanału jest poziome zbudowane z materiałów nierozmywalnych (wzmacniana masa
betonowa). W kanale mogą być umieszczone dwa filary mostu o przekroju kołowym
(średnica
φ
110) wykonane z tworzywa sztucznego (Polipropylen PP). Możliwa jest regulacja
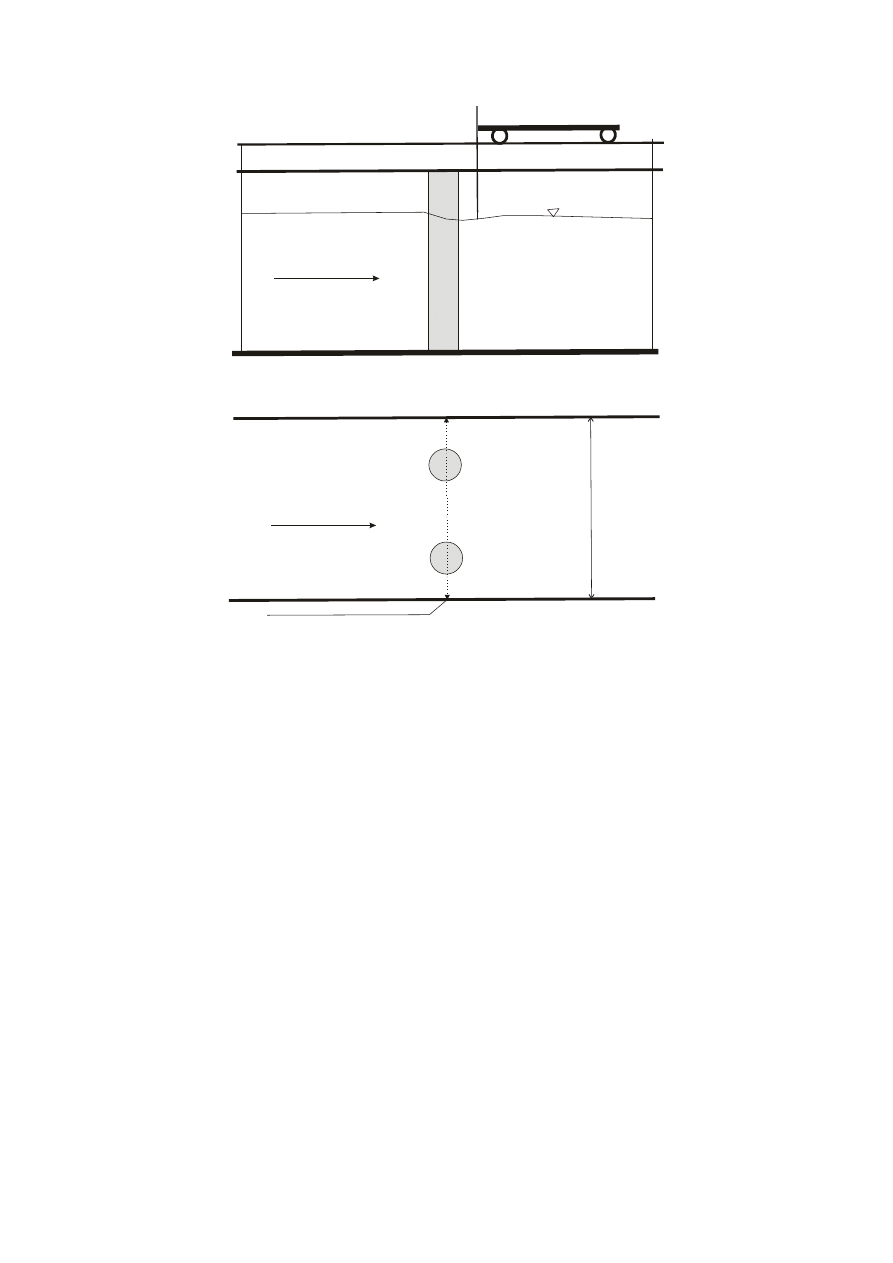
położenia filarów względem osi kanału (rys. 11).
13
dno kanału
przekrój podłó
ż
ny
fi
la
r
m
o
s
tu
1
1
0
Φ
kierunek przep
ływu wody
wózek pomiarowy
rzut z góry
fi
la
r
m
o
s
tu
1
1
0
Φ
kierunek przep
ływu wody
B
-
s
z
e
ro
k
o
ś
ć
k
a
n
a
łu
zwierciad
ło wody
s
z
p
ilk
a
p
o
m
ia
ro
w
a
przekrój mostowy (przekrój centralny)
Rys. 11. Schemat stanowiska pomiarowego
4. Przebieg ćwiczenia
1. Zmierzyć szerokość kanału laboratoryjnego;
2. Przygotować kanał laboratoryjny do przepływu wody bez obecności filarów mostu (wraz z
prowadzącym lub pracownikiem technicznym);
3. Po włączeniu pomp przez pracownika technicznego poczekać do ustalenia się przepływu w
kanale laboratoryjnym;
4. Zmierzyć wartość natężenia przepływu za pomocą kontrolnych przelewów o ostrej
krawędzi;
5. W dwóch przekrojach wskazanych przez prowadzącego zmierzyć rzędne dna i zwierciadła
wody, obliczyć spadek zwierciadła wody w kanale;
6. W przekroju mostowym pomierzyć rurką Prandla prędkości lokalne wody zgodnie z
rysunkiem 3b (Tabela 1), prowadzący może określić inną liczbę pionów pomiarowych;
7. Po zatrzymaniu przepływu zamontować filary mostu w przekroju mostowym (wraz z
prowadzącym lub pracownikiem technicznym);

14
8. Po ponownym włączeniu pomp z niezmienioną charakterystyką ich pracy sprawdzić, czy
rzeczywiste natężenie przepływu pozostało niezmienione (zgodnie z punktem 4);
9. Za pomocą wodowskazu szpilkowego wyznaczyć profil zwierciadła wody w osi kanału na
długości wskazanej przez prowadzącego. (Tabela 5);
10. Poniżej przekroju mostowego rurką Prandla pomierzyć prędkości lokalne wody zgodnie z
rysunkiem 3b (Tabela 1), prowadzący może określić inną liczbę pionów pomiarowych;
11. Korzystając z młynka hydrometrycznego pomierzyć charakterystyczne prędkości lokalne
w przekroju mostowym (Tabela 4);
5. Zawartość sprawozdania
Sprawozdanie powinno zawierać następujące elementy:
1.
Analiza hydrauliczna przepływu wody w kanale niezabudowanym
a.
Obliczenie wydatku kanału z formuły Manninga (równanie 2) i porównanie go
z wydatkiem rzeczywistym wyznaczonym przelewami kontrolnymi (punkt
2.1.4, Tabela 3);
b.
Określenie rozkładu prędkości w przekroju mostowym przy wykorzystaniu
rurki Prandla (punkt 2.1.2.1) wraz z rysunkiem izotach (rysunek 6);
c.
Obliczenie wydatku kanału w przekroju mostowym przy wykorzystaniu
metody Culmanna (punkt 2.1.2.3 i Tabela 2) i porównanie z wydatkiem
rzeczywistym (Tabela 3);
d.
Obliczenie składowych energii całkowitej mechanicznej i określenie formy
ruchu burzliwego na długości kanału (równanie 16);
e.
Narysowanie przekroju podłużnego zwierciadła wody i linii energii całkowitej
płynącej wody (rys. 8).
2.
Analiza hydrauliczna przepływu wody w kanale zabudowanym filarami mostu
a.
Określenie
rozkładu
prędkości
poniżej
przekroju
mostowego
przy
wykorzystaniu rurki Prandla (punkt 2.1.2.1) wraz z rysunkiem izotach
(rysunek 6);
b.
Obliczenie wydatku kanału poniżej przekroju mostowego przy wykorzystaniu
metody Culmanna (punkt 2.1.2.3 i Tabela 2) i porównanie z wydatkiem
rzeczywistym (Tabela 3);
c.
Obliczenie składowych energii całkowitej mechanicznej i określenie form
ruchu burzliwego na długości kanału (Tabela 5, równanie 19,20);

15
d.
Na rysunku wykonanym w punkcie 1e narysowanie przekroju podłużnego
zwierciadła wody, linii głębokości krytycznej oraz linii energii całkowitej
(rys.10). W miejscach, gdzie nie policzono prędkości średniej, punkty
odpowiadające energii całkowitej łączyć linią przerywaną (patrz: uwaga do
tabeli 5);
e.
Rozpoznanie i opisanie prędkości lokalnych w przekroju mostowym przy
wykorzystaniu młynka hydrometrycznego (Punkt 2.1.2.1, Tabela 4).
Uwaga: należy zamieścić przykładowe obliczenia wartości zawartych w tabelach
3.
Podsumowanie i wnioski.
6. Literatura:
[1] Laboratorium z mechaniki płynów i hydrauliki – praca zbiorowa pod kierunkiem K.
Weinerowskiej, Politechnika Gdańska, Gdańsk 2004 (skrypt wydany w formie
elektronicznej).
[2] Laboratorium z mechaniki płynów i hydrauliki – praca zbiorowa, Politechnika Gdańska,
Gdańsk 1995.
[3] Hydraulika techniczna – przykłady obliczeń, Kubrak E. i Kubrak J., Wydawnictwo
SGGW, Warszawa 2004.
[4] Rozp. Min. Transportu i Gospodarki Morskiej z dnia 30 maja 2000 r. w sprawie
warunków technicznych, jakim powinny odpowiadać drogowe obiekty inżynierskie i ich
usytuowanie – Dz.U. Nr 63 poz. 735.
[5] Byczkowski A., Hydrologia, Wyd. SGGW 1996.
[6] Madaj A., Wołowicki W., Podstawy projektowania budowli mostowych, WKŁ Warszawa
2007.
7. Przydatne informacje do wykonania ćwiczenia:
Zasada pomiaru natężenia przepływu za pomocą przelewu o ostrej krawędzi
Należy zapoznać się z rozdziałem II/4 (str. 32) skryptu
Laboratorium z mechaniki płynów i
hydrauliki [1].
Współczynniki oporów liniowych przy przepływie cieczy w kanałach otwartych
Należy zapoznać się z rozdziałem II/3 (str. 29) skryptu
Laboratorium z mechaniki płynów i
hydrauliki [1].
Podstawy teoretyczne przepływu wody w kanałach otwartych

16
Należy zapoznać się z rozdziałem III/4.1 (str. 111) skryptu
Laboratorium z mechaniki płynów
i hydrauliki [1].
Określenie szerokości zwierciadła wody w przekroju poprzecznym w którym znajduje
się filar mostu.
W ćwiczeniu filary mostu imitują rury o przekroju kołowym. Aby uzyskać szerokość
zwierciadła wody B, należy od szerokości kanału laboratoryjnego odjąć szerokości filarów w
odpowiednim przekroju. W przekroju centralnym (rys. 11) szerokość zwierciadła wody
pomniejszona będzie o średnice filarów 220 mm (22cm) względem szerokości kanału. W
każdym innym przekroju, szerokości filarów są zmienne i można je zmierzyć na podstawie
wykonanego w skali rzutu z góry kanału laboratoryjnego.
17
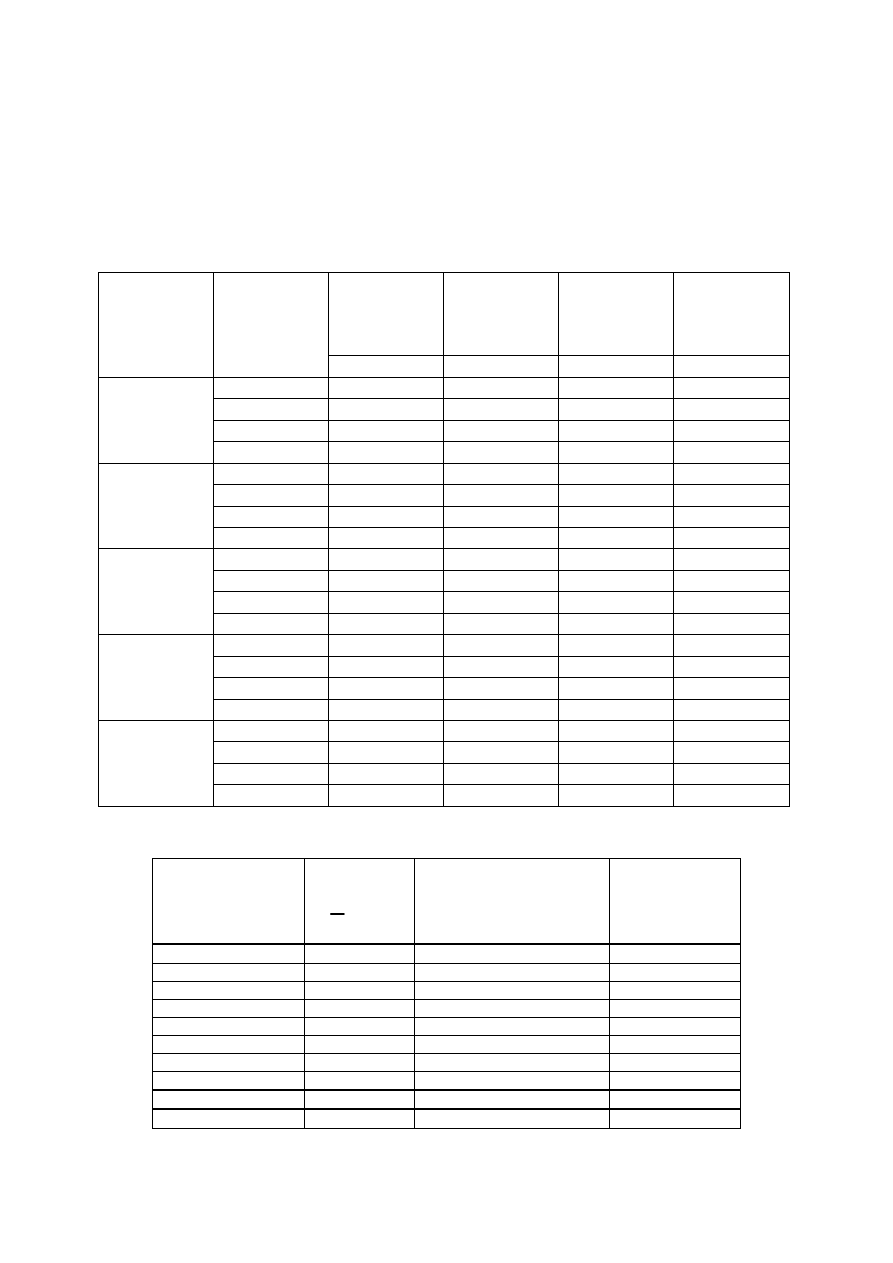
Tabela 1. Obliczenie prędkości lokalnych rurką Prandla
Przekrój …………………………………………
Nr przekroju ……………………………………
Data i godzina pomiaru …………………………
Wydatek kontrolny ………………..m
3
/s …………………dm
3
/s ……………..cm
3
/s
Pion
(odległość
od brzegu
lewego)
Punkt
Wysokość
punktu od
dna
z
i
∆∆∆∆
h
i
v
Li
V
Li
cm
cm
cm/s
m/s
1
I
2
3
……………
4
1
II
2
3
……………
4
1
III
2
3
……………. 4
1
IV
2
3
……………
4
1
V
2
3
……………
4
Tabela 2. Obliczenie natężenia przepływu metodą Culmanna
Izotachy
odpowiadające
prędkościom
[m/s]
Prędkość
średnia
v
[m/s]
Powierzchnia
zawarta pomiędzy
izotachami
∆∆∆∆
A [m
2
]
Natężenie
przepływu
∆∆∆∆
Q [m
3
/s]
Q=
m
3
/s
Q=
dm
3
/s
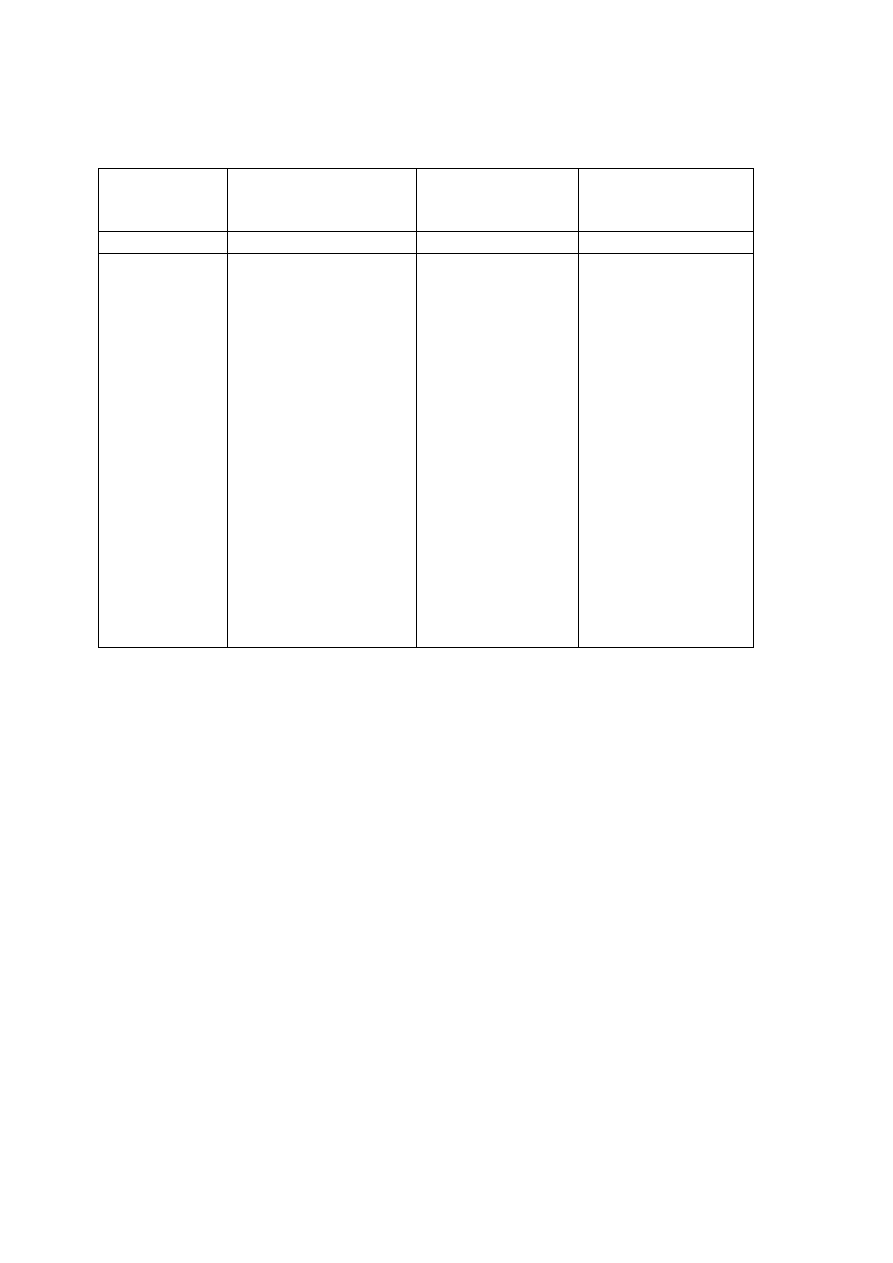
18
Tabela 3. Zestawienie wyników pomiarów i obliczeń natężenia przepływu w kanale
Wydatek
rzeczywisty
Wydatek w korycie
niezabudowanym z
równania Manninga
Wydatek w korycie
niezabudowanym z
metody Culmanna
Wydatek w korycie
zabudowanym z
metody Culmanna
dm
3
/s
dm
3
/s
dm
3
/s
dm
3
/s
Natężenie
przepływu z
przelewu
kołowego 1
…………dm
3
/s
Natężenie
przepływu z
przelewu
kołowego 2
…………dm
3
/s
SUMA
…………dm
3
/s
19
Tabela 4.
KARTA POMIARÓW HYDROMETRYCZNYCH
Rzeka: ………….. Data: ………………………………………
Przekrój: ……………
godzina
stan [cm]
warunki atmosferyczne
początek
koniec
Młynki
α
αα
α
ββββ
A
B
C
D
E
Nr
pionu
Odległość
[m]
Głębokość
pomiaru
[m]
Liczba
impulsów
Średnia
liczba
impulsów
Liczba
obrotów
[1/s]
Młynek
v
[m/s]
Uwagi
20
Tabela 5. Analiza całkowitej energii mechanicznej na długości kanału otwartego dla koryta zabudowanego
Przekrój nr
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29
Odległość [cm]
Rzędna zw.
wody w osi
kanału R
zw
[cm]
Głębokość
h=R
zw
-RD [cm]
Prędkość
ś
rednia v
[cm/s]
Wysokość
prędkości
g
v
2
2
α
[cm]
Wysokość
energii
rzeczywistej
(równanie 16)
g
v
h
E
2
2
α
+
=
[cm]
głębokość
krytyczna
(równanie 17)
h
kr
[cm]
Rzędna dna kanału pomiarowego RD: …………… cm
UWAGA: W przekrojach, gdzie rzędna zwierciadła wody zależy od warunków lokalnych (spiętrzenie przed filarem mostowym, obniżenie za
filarem mostowym, istotna zmiana głębokości wody w przekroju poprzecznym) NIE LICZYĆ prędkości średniej, wysokości prędkości oraz
wysokości energii całkowitej. W odpowiednie kratki wstawić X.
Wyszukiwarka
Podobne podstrony:
Analiza przepływu wody przez przekrój mostowy (FM)
Analiza przepływu wody przez przekrój mostowy (FM)
Współczynnik wodoprzepuszczalności gruntu k określa prędkość przepływu wody przez grunt przy spad ,
Analiza przeplywu przez przepus Nieznany (2)
Przepływ energii przez ekosystem
1 ćwiczenie (Analiza jakościowa wody) OZNACZANIE CHLORKÓW I SIARCZANÓW
Przeplyw wody w gruncie, naprez Nieznany
analiza przeplywow, BANKOWOŚĆ, Bankowość i Finanse
Monitoring hydrometeorologiczny „Pomiar stanu i przepływu wody”
Przepływ cieczy przez duży otwór
Transport wody przez korzen
Opór liniowy podczas przepływu płynu przez przewód
1 ćwiczenie (Analiza jakościowa wody) OZNACZANIE ZWIĄZKÓW AZOTU
wyplyw wody przez maly otwor karta
Ustalony przepływ cieczy przez duży otwór
więcej podobnych podstron