Sprawozdanie 3

Autor: Mateusz Gąsiorek

Przedmiot: Modelowanie i identyfikacja

Termin: ŚR 13:15

Prowadzący: dr Paweł Wachel

Sprawozdanie zawiera zakres 4 tematów:

Laboratorium 9 - estymator ortogonalny Gassera-Mullera funkcji regresji

Laboratorium 10 - układ identyfikujący parametry systemu Hammesteina metodą korelacyjną

Laboratorium 11 – model ARMA

Laboratorium 12 – model ARMA (poprawki)

LABORATORIUM 9

1. Opis ćwiczenia.

Cele ćwiczenia było zbudowanie estymatora ortogonalnego Gassera-Mullera funkcji regresji.
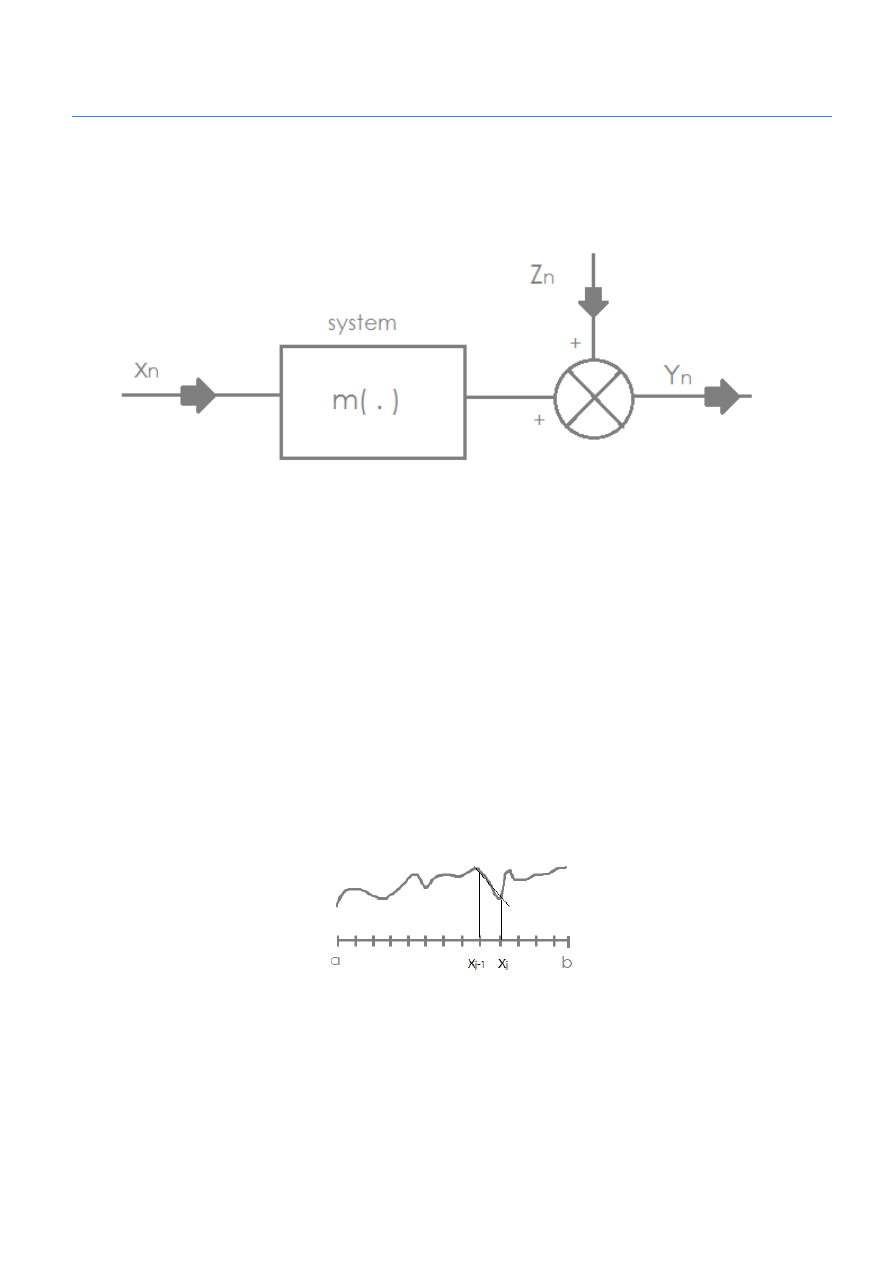
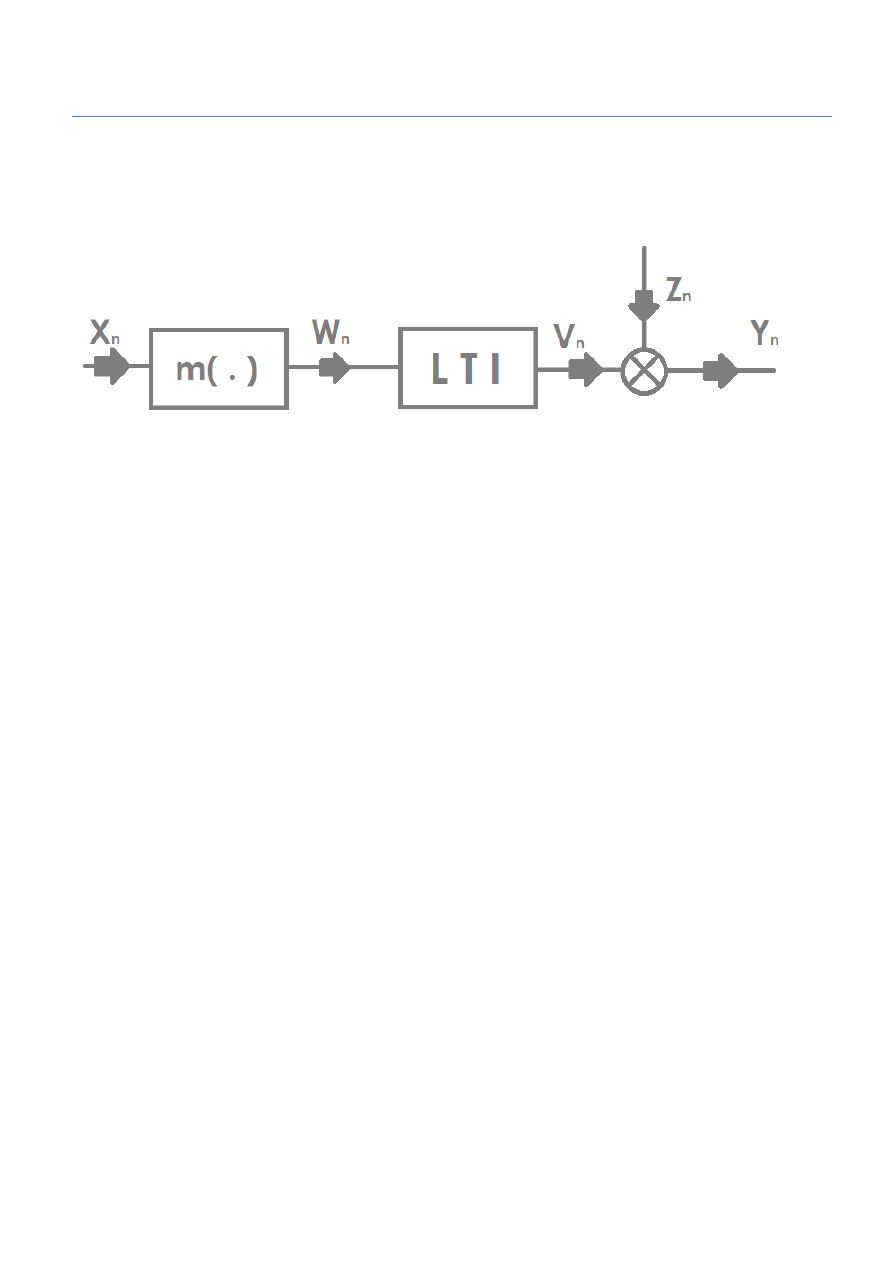
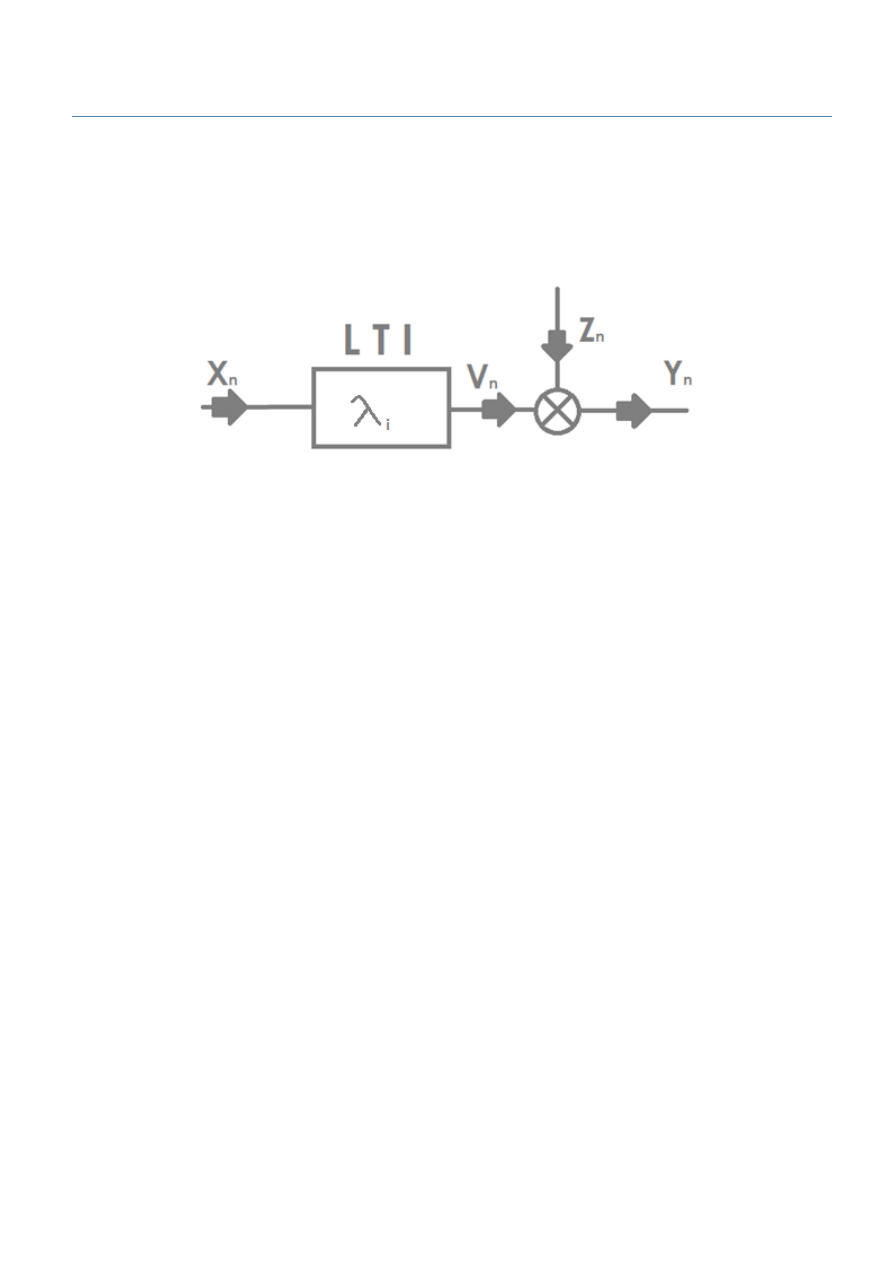
W tym celu symulowano działanie układu zobrazowanego poniżej:

Rysunek 1 - rysunek pomocniczy badanego układu

W ramach ćwiczenia przyjmujemy że:



– jest posortowanym wejściem (ciąg deterministyczny)



– zakłócenia ciągłe, o zerowej wartości oczekiwanej i posiadające wariancję.



( ) pozwala przedstawić system w bazie ortogonalnej.

Celem ćwiczenia było

na wyjściu układu.

Estymator ortogonalny wyznaczany w ramach poprzednich laboratoriów opisany był wzorem:

( ) ∑

( )

Gdzie:

( )

( )

Następnie zakładamy że dzielimy obszar tak aby najdłuższa odległość

Rysunek 2 - schemat dzielenia obszaru na mniejsze.

Z czego wynika :

∑ ∫

( )

( )

Gdzie po przekształceniach otrzymujemy:

̂ ∑

∫

( ) ∑

(

)

(

)

2. Badania.

W ramach laboratorium należało przetestować wpływ liczby próbek na błąd estymacji,
sprawdzić zachowanie estymatora na zmianę sygnału na funkcję nieciągłą. Dodatkowo
przebadano wpływ uproszczonego estymatora.

I.

Funkcja ciągła.

Pierwszy test wykonano dla liczby próbek N=100 oraz funkcji y=x, widać jednak że dla
zwiększającej się liczby próbek N wartość błędu będzie coraz mniejsza, dlatego w dalszej
części testy przeprowadzano dla N=2000 (jest to optymalna wartość dla krótkiego czasu pracy
programu jak i dokładności wartości wyjściowych).

Zadano kilka przykładowych funkcji ciągłych i przebadano je dla ilości próbek N=2000.

( ) ( ) ( )

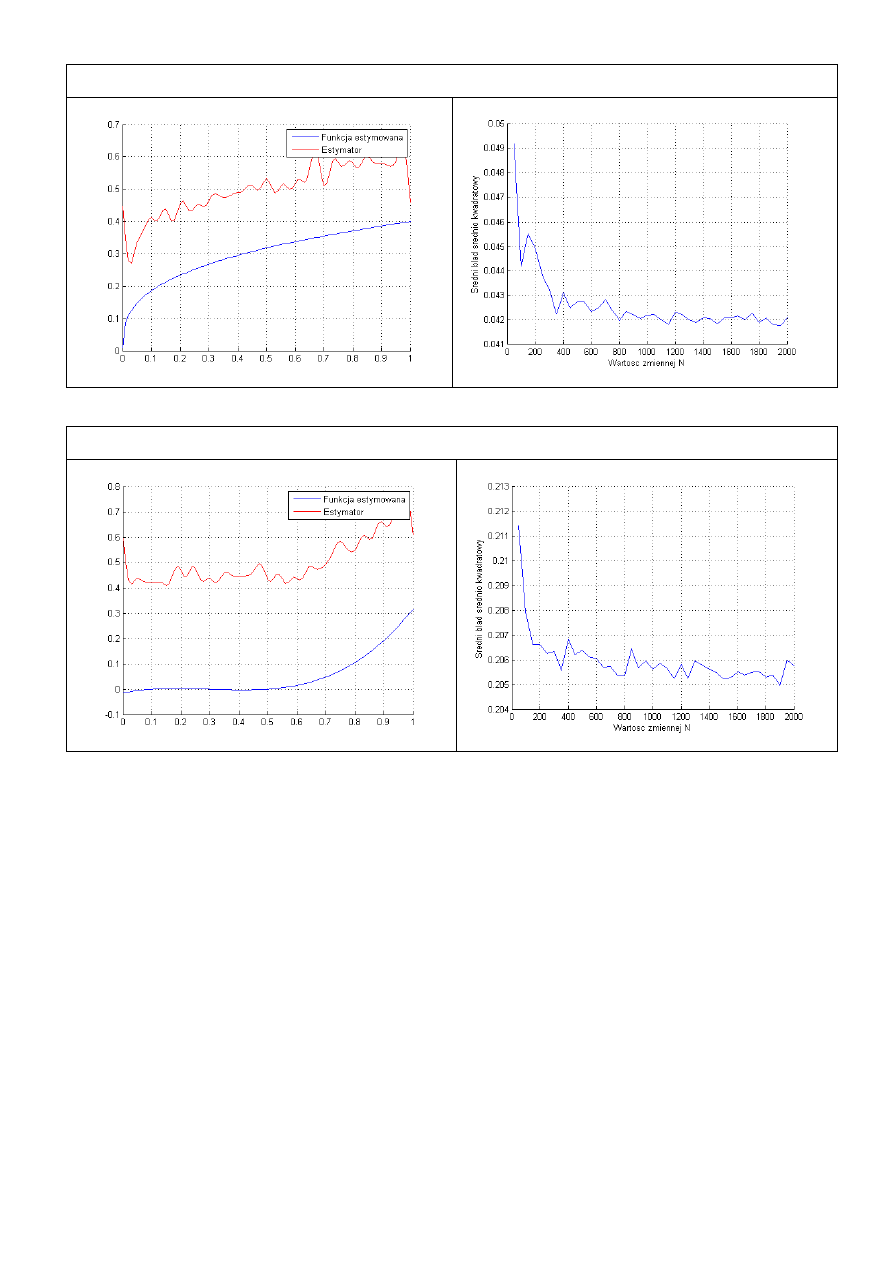
Widać że estymator w zależności od funkcji przyjmuje różne wartości. Najlepsza estymacja jest
dla funkcji liniowej y=x. Jej błąd dla liczby próbek N=2000 zbiega do 0 i osiąga wartość około
0.004. Przy funkcjach o wielu miejscach zerowych (funkcja 3) wykres jest oddalony o pewną
wartość od funkcji estymowanej, jednak błąd również zbiega do 0. Przyjmuje on jednak
wartość prawie 2 rzędy większą niż w przypadku funkcji liniowej.

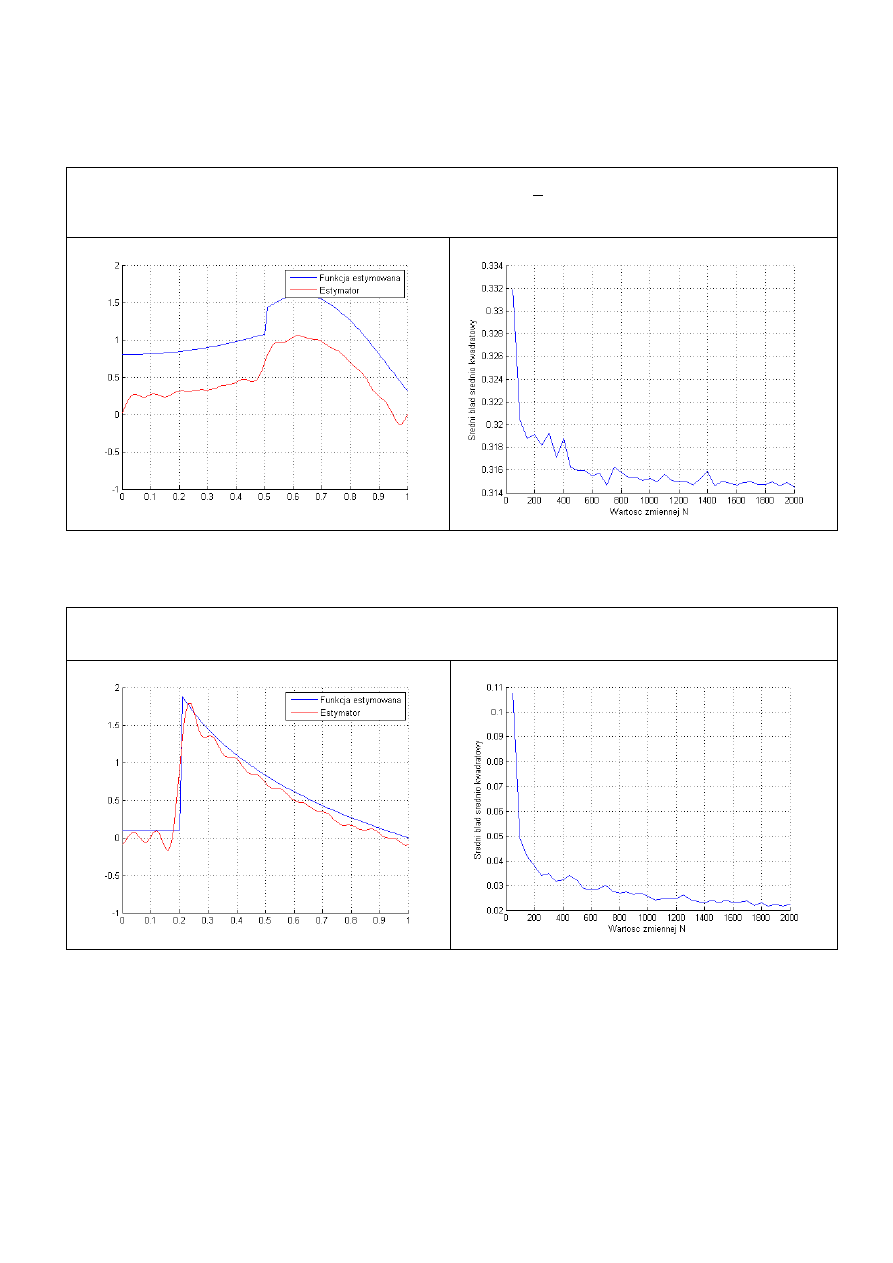
II.

Funkcja nieciągła.

Dodatkowo zadano kilka funkcji nieciągłych określonych różnymi wzorami:



I funkcja

( )



II funkcja

( )



III funkcja

( )



IV funkcja

(

)

(

)



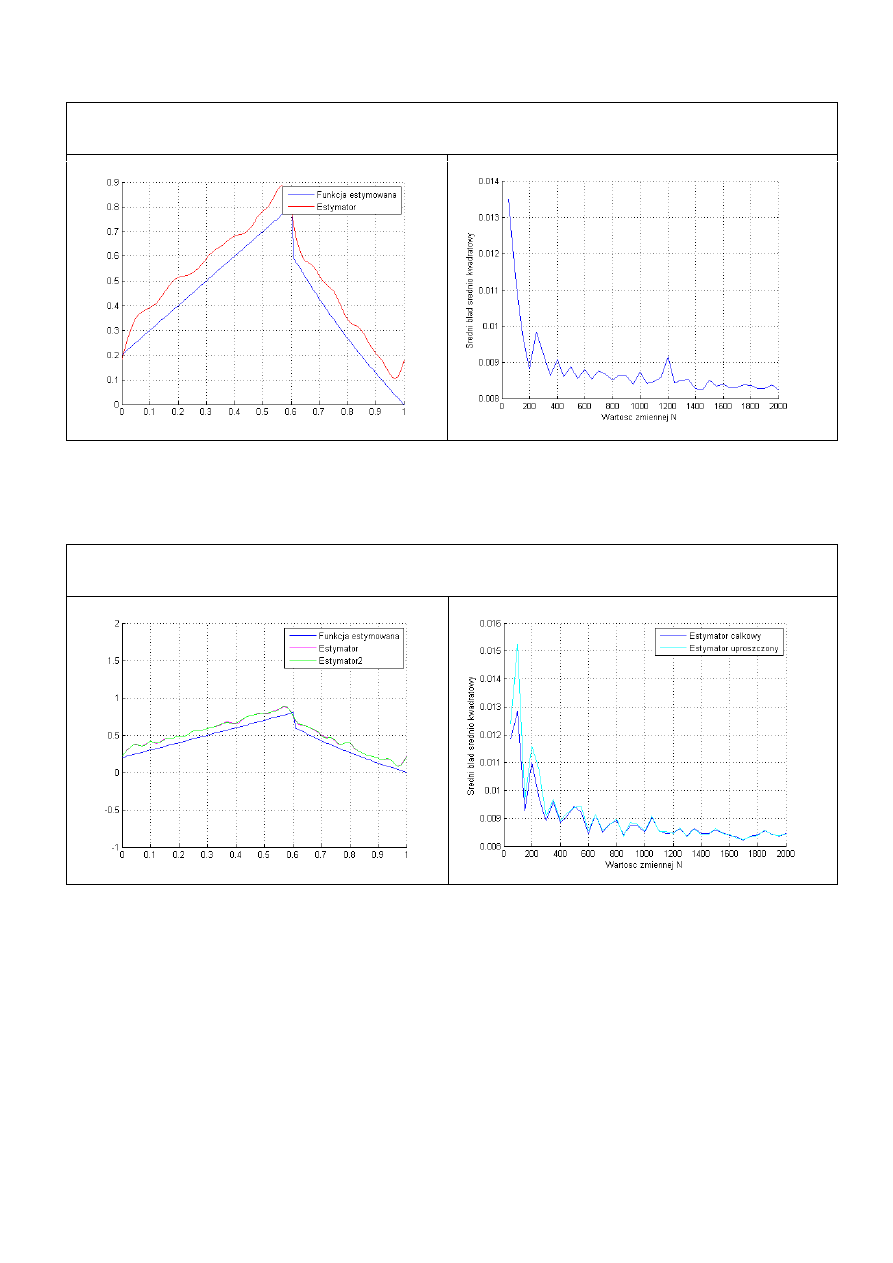
V funkcja

( )

III.

Badanie estymatora uproszczonego w porównaniu do całkowego.

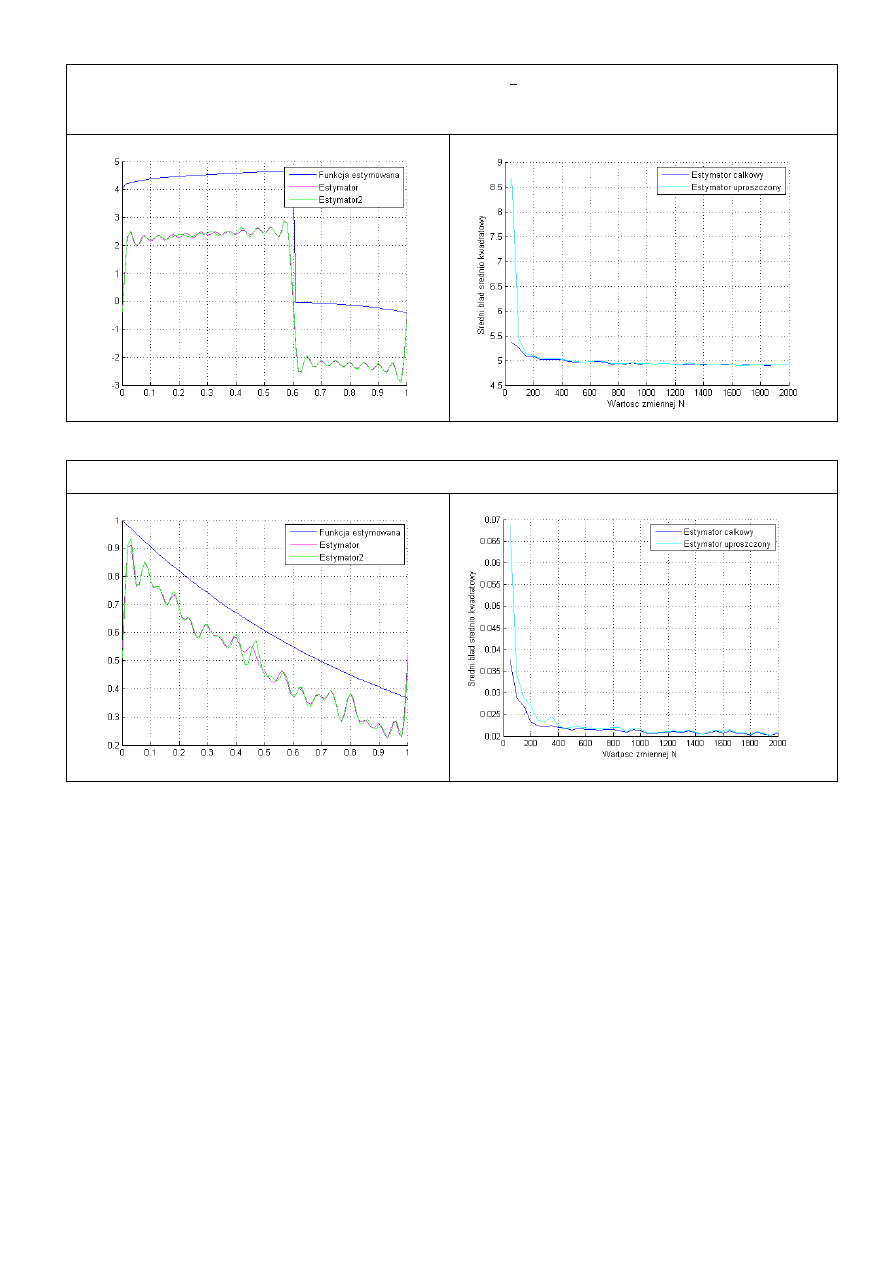
Przebadano kilka przykładowych funkcji aby pokazać wpływ uproszczonego estymatora.

( )

(

)

(

)

Z powyższych wykresów funkcji nieciągłej widać że różnica pomiędzy estymatorem
całkowym, a uproszczonym jest nieznaczna (biorąc pod uwagę wartość funkcji). Jak widać z
drugiej pary wykresów estymator całkowy, przyjmuje prawie dwukrotnie mniejszą wartość
błędu w pierwszych 100 pomiarach. Oba wykresy wskazują na to że błąd średniokwadratowy
dla wartości uproszczonej zbiega również do 0 jednak dla małych wartości N przyjmuje
większe wartości.

3. Wnioski.

Z powyższych wykresów można łatwo zauważyć że wpływ estymator radzi sobie z większością
funkcji ciągłych jak i nieciągłych. Ważnym aspektem jest odpowiedni dobór funkcji, gdyż zbyt
złośliwe dobranie przedziałów na których następuje nagła zmiana funkcji skutkuje
niedokładnością estymacji i aproksymacją liniową całego przedziału (0,1). We wszystkich
badanych funkcjach błąd estymacji w zależności od liczby próbek N maleje do 0 w
określonym dla zadanej funkcji wejściowej tempie. Estymacja uproszczona znacznie
przyśpiesza cykl pracy programu zmniejszając go prawie 3 rzędy. Można również wyciągnąć
wniosek na temat doboru funkcji estymowanej. Z wykresów zamieszczonych w I i II pkcie
można zauważyć że estymator lepiej radzi sobie z funkcjami harmonicznymi. Wynika to z faktu
wykorzystania e estymatorze funkcji trygonometrycznych.

Laboratorium 10

1. Opis ćwiczenia.

Celem ćwiczenia było utworzenie układu identyfikującego parametry systemu Hammesteina
metodą korelacyjną. W tym celu utworzono układ zaprezentowany poniżej:

Rysunek 3 - schemat układu wykorzystującego metodę korelacji.

W trakcie laboratorium przyjęto następujące warunki:







– zakłócenia ciągłe, o zerowej wartości oczekiwanej i posiadające wariancję.

Poszczególne wyjścia systemu przedstawiono:



(

)



∑





Układ ten składa się z dwóch bloków nieliniowego dynamicznego oraz statycznego liniowego.

Wartość oczekiwana zbiega do wartości

, gdzie c jest wartością oczekiwaną

odpowiedzi członu m( . )

2. Badanie

System pobudzano sygnałem losowym o wartości oczekiwanej =0, oraz wariancji =1. Jako
zakłócenie przyjęto zgodnie założeniem sygnał o wartości oczekiwanej =0 i wariancji =0.1.
Badano dwa przypadki:



Zaproponować postać estymatora współczynników odpowiedzi, gdy wariancja jest
znana, ale nie jest równa 1,



Zaproponować postać estymatora współczynników odpowiedzi, gdy wariancja jest
znana, i jest równa 1,

Układ przetestowano dla 13 różnych wartości: 10 50 100 150 200 300 400 500 600 700 800 900
1000.

I.

Wzór na estymator przedstawia się następująco:

( )

∑

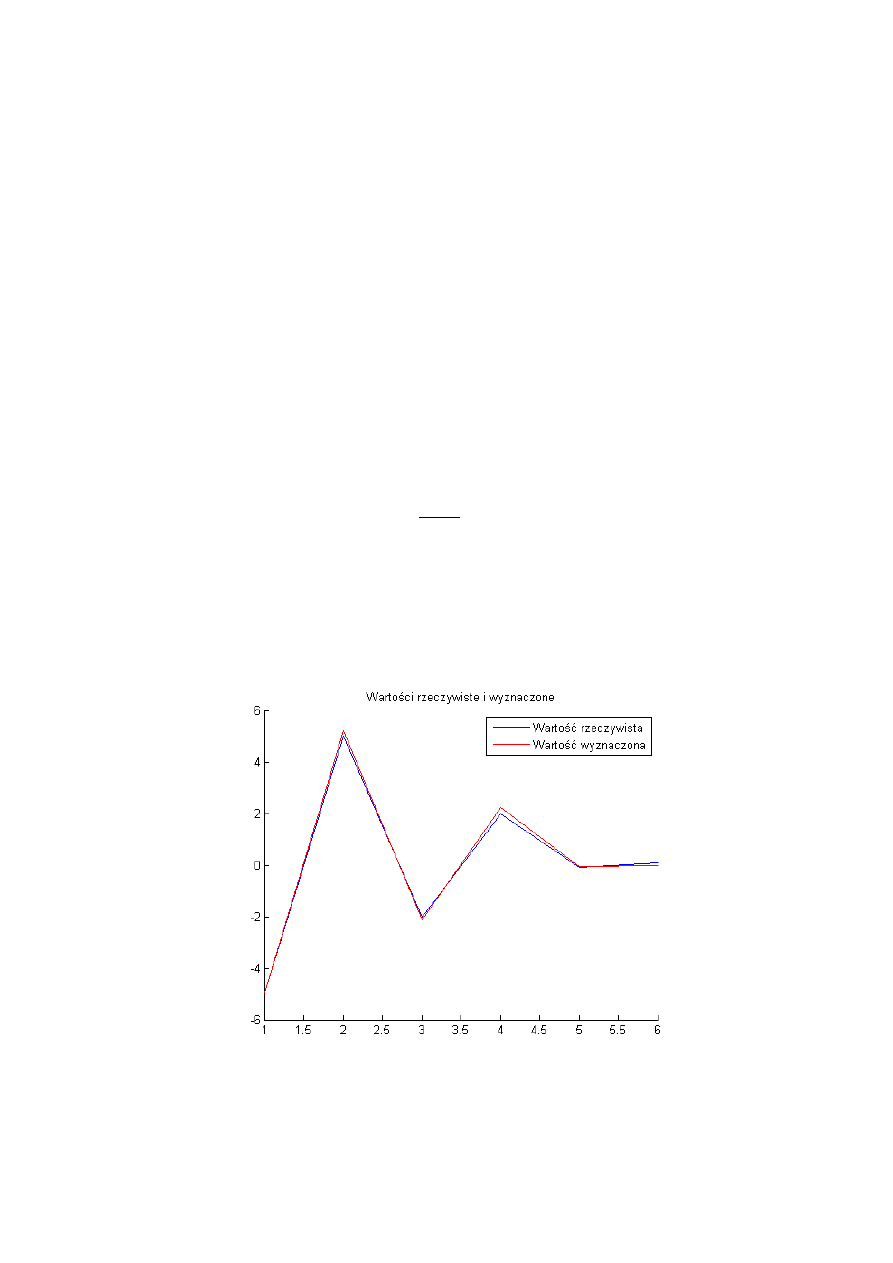
Poniżej przedstawiono wykres współczynników odpowiedzi impulsowej, które należy
estymować, w celu dokładniejszego przedstawienia ich na wykresie punkt połączono linią. (

-5

5 -2 2 -0.1 0.1 ) oraz wartości estymowane.

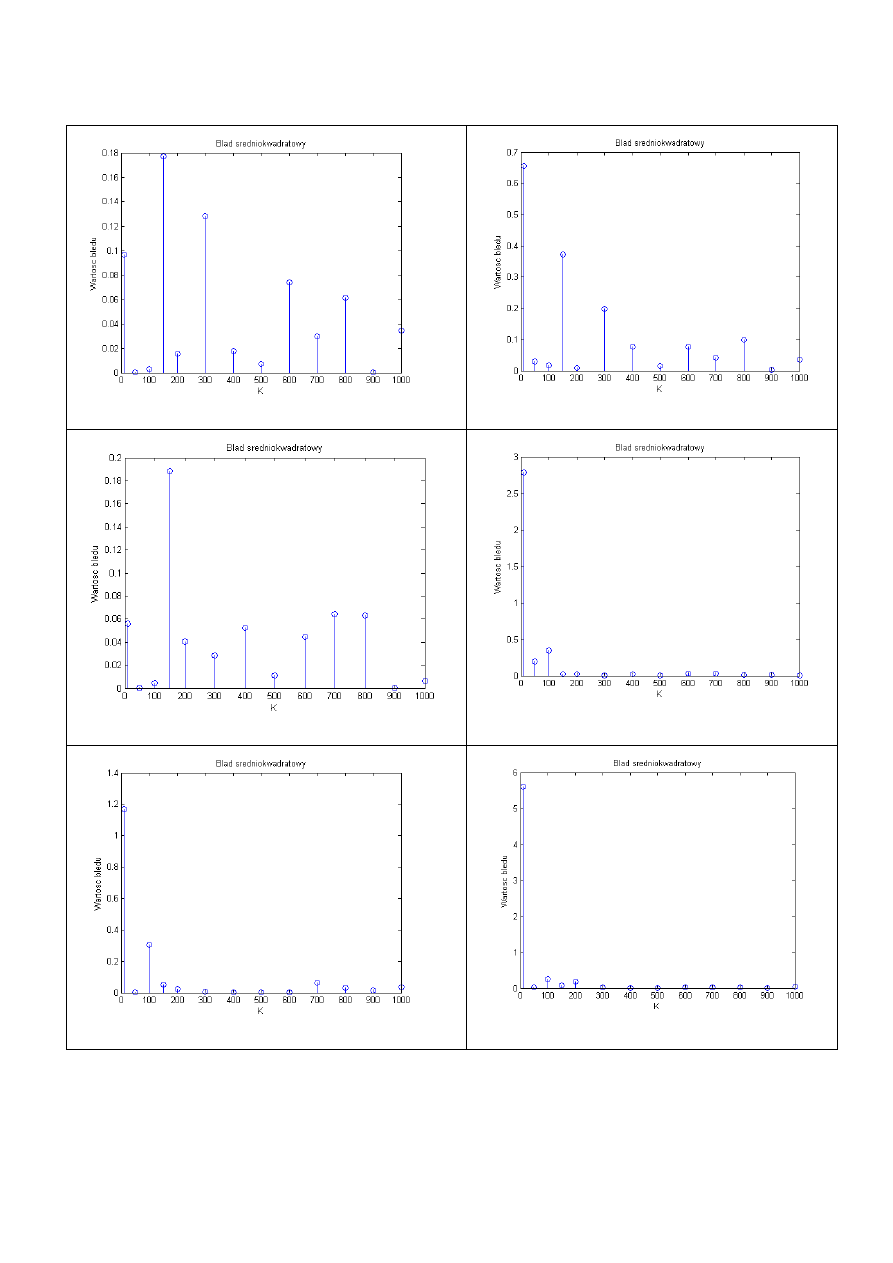
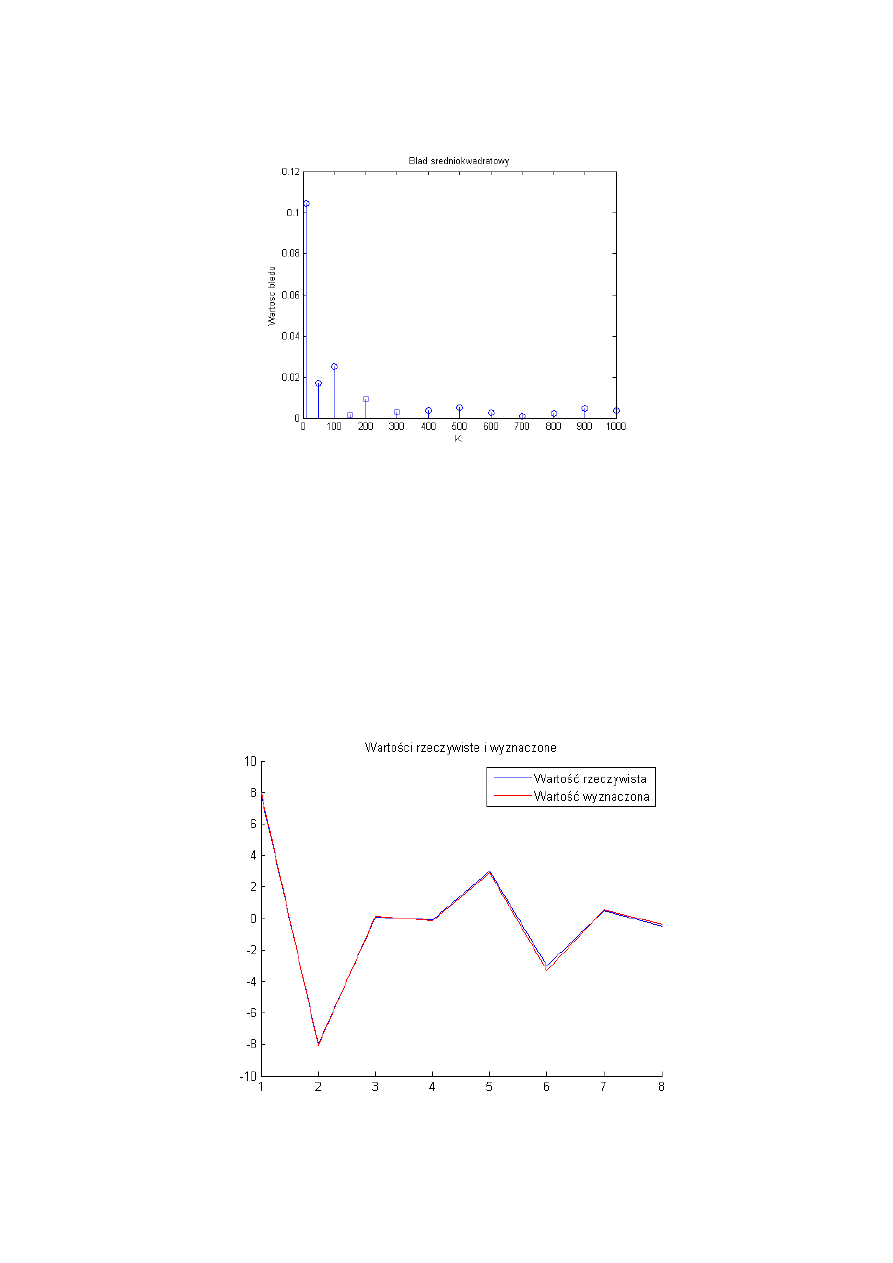
Następnie wygenerowano wartości błędów przy zwiększającej się liczbie powtórzeń dla
poszczególnych współczynników:

b1

b2

b3

b4

b5

b6

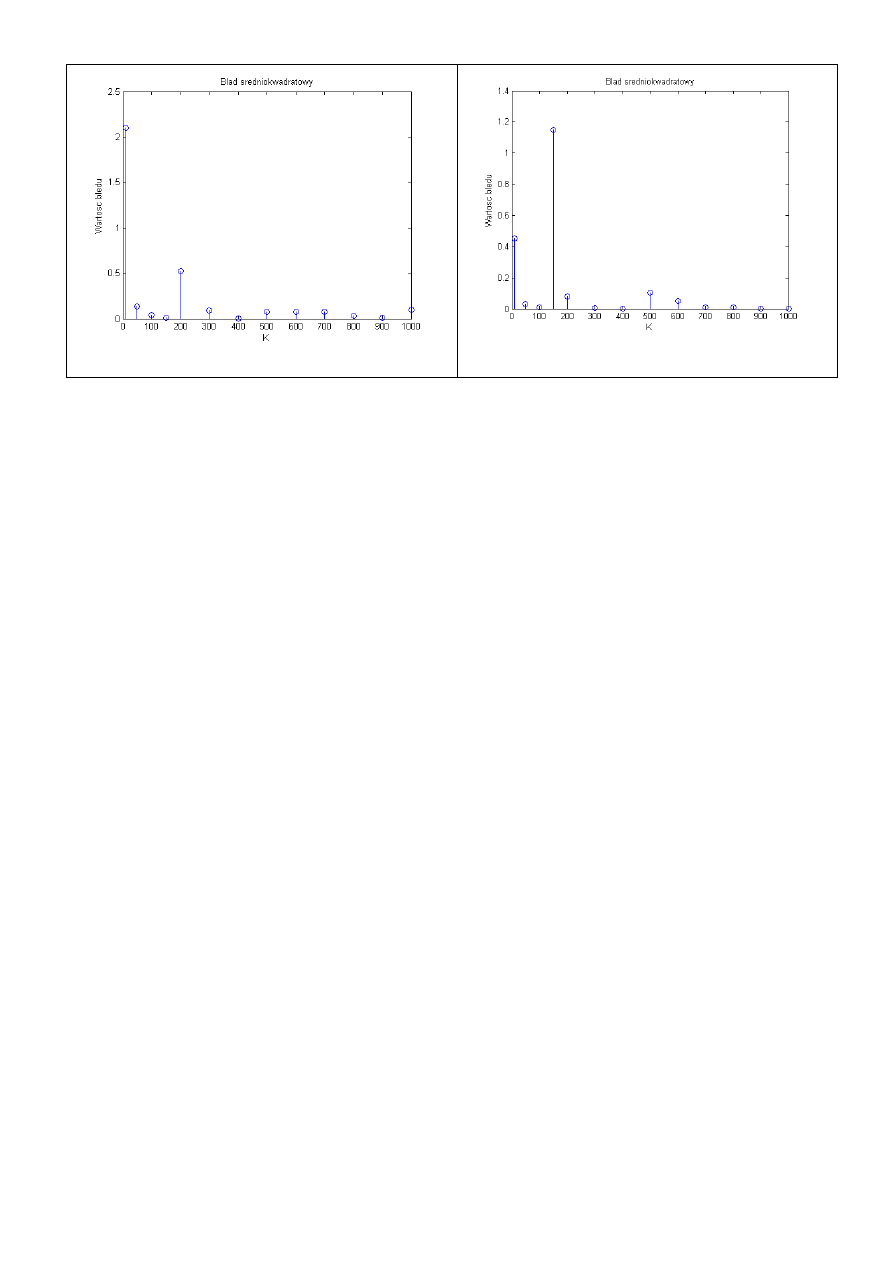
Poszczególne wykresy pokazują że współczynniki te zostają dobrze estymowane. Wartość
błędu dla małej liczby próbek jest duża (kilku, kilkunasto-krotnie większa niż dla liczby K>100),
jednak przy błąd średniokwadratowy zbiega do 0.

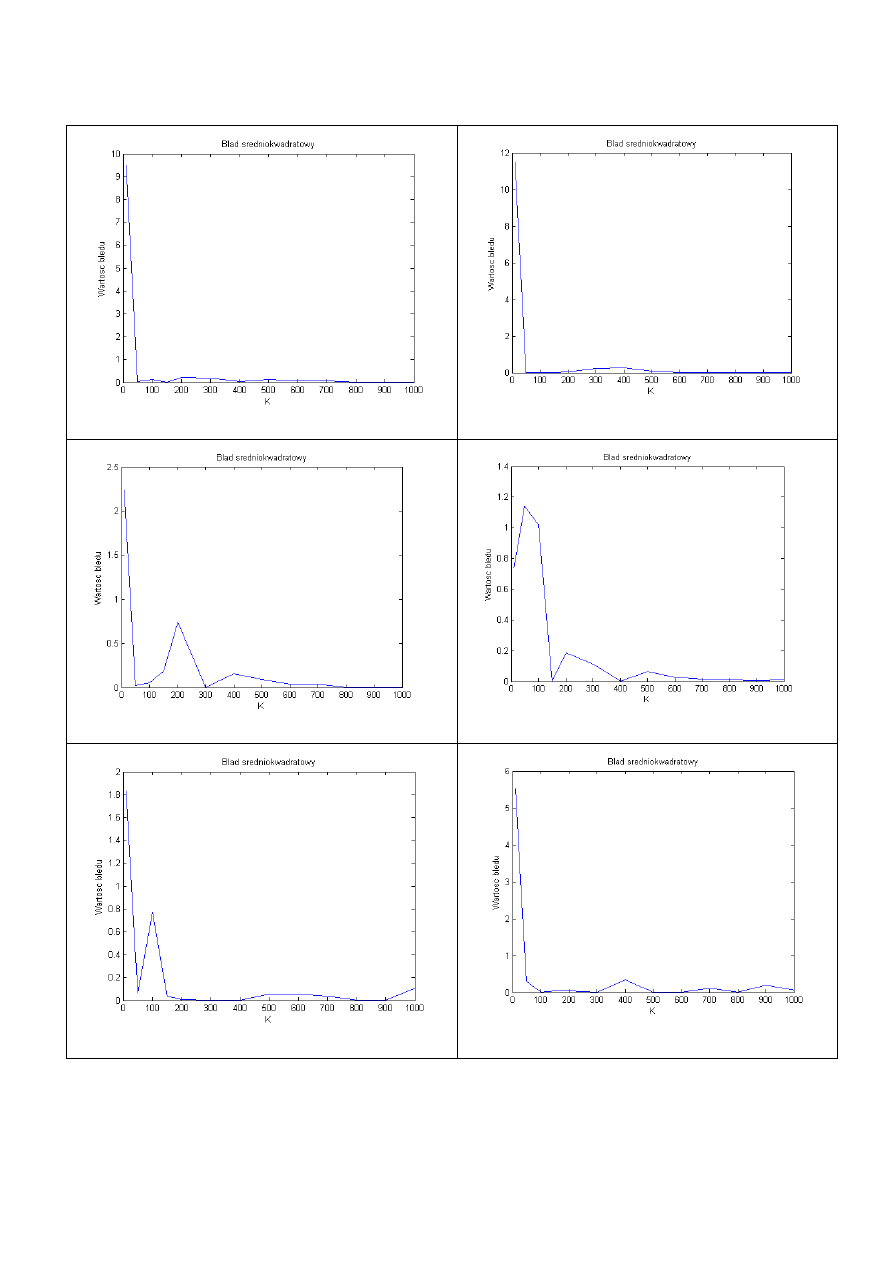
Zwiększając natomiast liczbę powtórzeń obliczeń możemy doprowadzić do spadku wartości
błędu średniokwadratowego gdzie dla ostatniego parametru [b6] (gdzie błąd dla K=10
wynosił około 5,7) wygląda następująco (n=100):

Wartość błędu przy 100 powtórzeniach obliczeń jest prawie 100x mniejsza niż dla 5 powtórzeń.
Wynika z tego że zwiększając liczbę powtórzeń zmniejszamy błąd początkowy wyznaczania
współczynników (ten zaś wynika z losowości). Należy jednak pamiętać że są to wartości
punktowe błędów szacujące jakość estymatora. Pojedynczy punkt wynoszący 7 wpływa
znacząco na jakość estymacji, oznacza to ogromną różnicę w wartości estymowanej.

Następnie badania przeprowadzono zmieniając tablicę współczynników a

0 8 -8 0.1 -0.1 3 -3 0.5 -0.5

Poniżej zaprezentowano współczynniki rzeczywiste oraz estymowane:

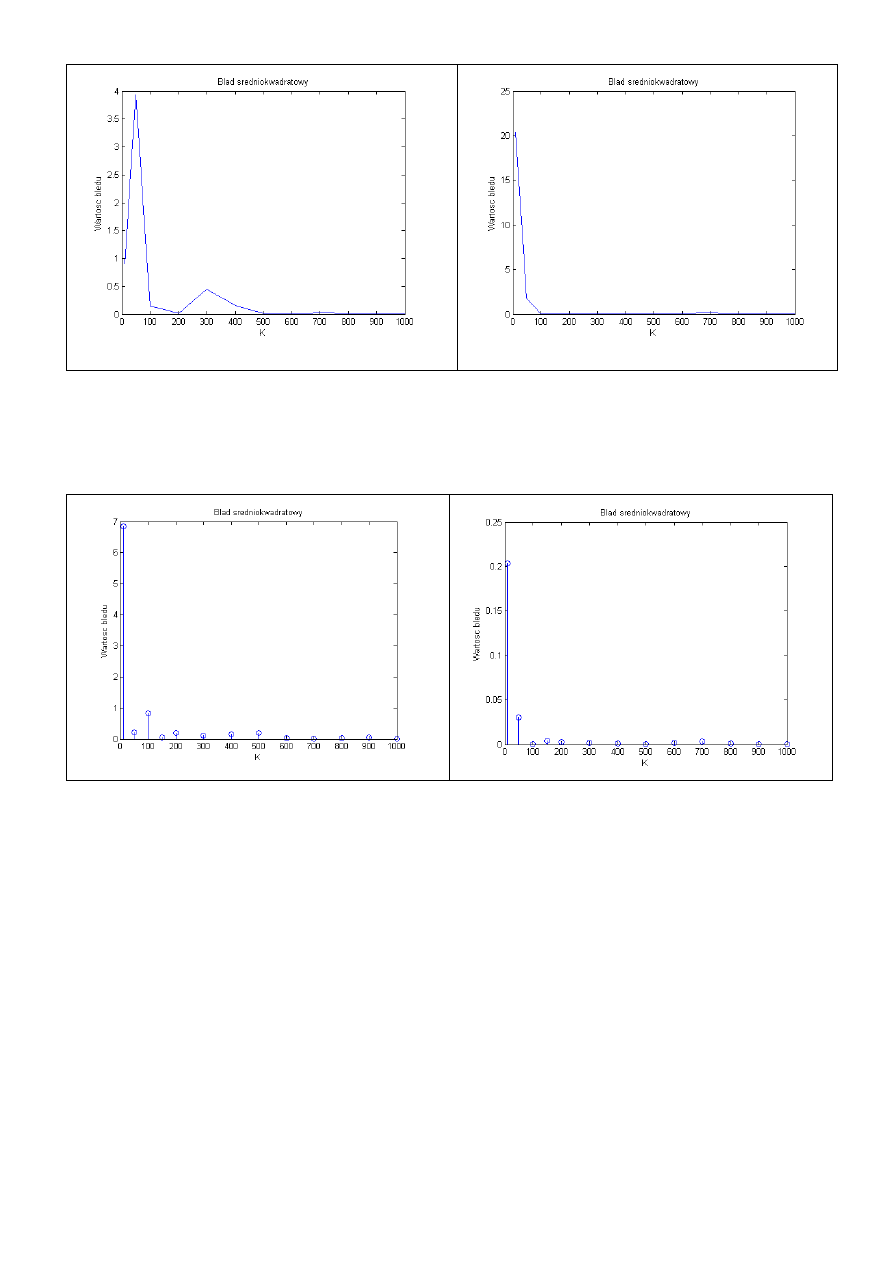
W kolejnym kroku przebadano wyznaczenie dla ośmiu współczynników (w celu łatwiejszego
odczytania wartości wykresy połączono linią).

B1

B2

B3

B4

B5

B6

b7

B8

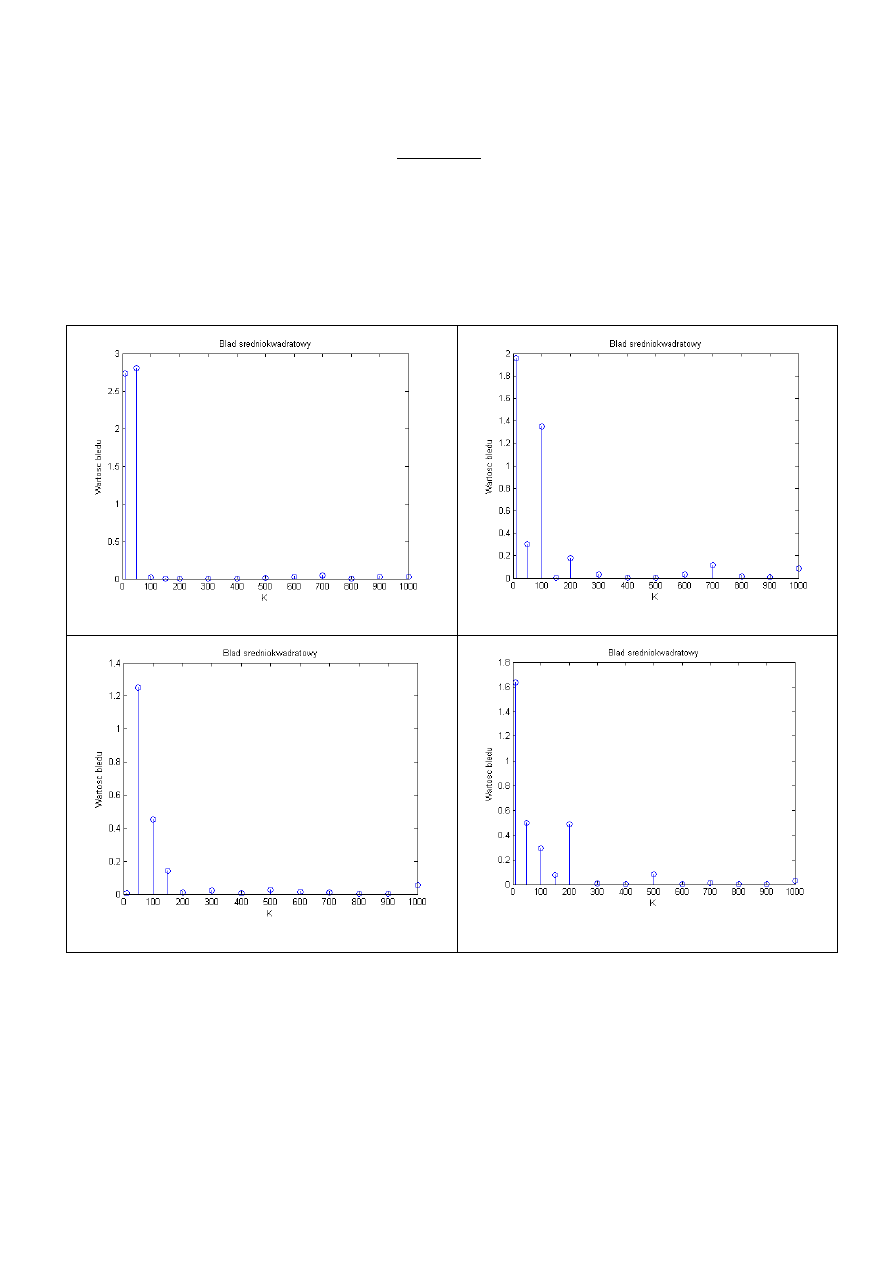
W ostatnim kroku przebadano układ dla 4 zmian kierunku (wykres powyżej), w zależności od
liczby powtórzeń. Wykres po lewej stronie (poniżej) pokazuje wartość błędu dla 10 powtórzeń, i
dla ósmego parametru , wykres po prawej dla 100 powtórzeń ósmego parametru.

II.

( )

Wzór z punktu I działa tylko dla wariancji =1, wzór ten należy udoskonalić

( )

( )

∑

Analogiczny eksperyment przeprowadzono dla ulepszonej estymacji. Badano 6 parametrów
ponieważ w poprzednim doświadczeniu wykazano brak wpływu liczby parametrów na
estymację.

b1

b2

b3

b4

b5

b6

Ponownie widać, że parametry odpowiedzi impulsowej zostały wyestymowane właściwie. I
ponownie wraz ze wzrostem K maleje błąd średniokwadratowy.

3. Wnioski.

Jak widać zaproponowany estymator współczynników odpowiedzi impulsowej, z drobnymi
modyfikacjami, bądź dodatkowymi obliczeniami, działa poprawnie. Przy rosnącej wartości
ilości sumowań K błąd średniokwadratowy znacząco się zmniejsza, zmierzając do 0. Edycje
wzoru estymatora polegały na prostych zabiegach matematycznych. Przy wariancji różnej niż
1 należało podzielić cały wzór przez tą wariancję. Natomiast przy wartości oczekiwanej różnej
od 0, należało odjąć od wszystkich zmiennych wartość oczekiwaną. Wiąże się to z tym, że
wzór estymatora w podstawowej wersji jest poprawny tylko dla wariancji = 1 i wartości
oczekiwanej = 0. Aby go uogólnić, to należy „sprowadzić” te parametry zmiennej losowej, do
takiej właśnie postaci.

Z wykresów porównawczych dla zmiennej liczby próbek n widać że zwiększenie liczby
powtórzeń zmniejsza wartość błędu, a co za tym idzie polepsza wynik programu. Jednak ze
względów obliczeniowych przedstawiono przykładowe wykresy dla wartości próbek 100,
pozostałe wykonywane są dla małej ilości powtórzeń w celu pokazania innych wniosków.

Laboratorium 11 + 12

1. Opis ćwiczenia

Należało zamodelować układ ARMA składający się z dwóch członów:



AR (model autoregresyjny),



MA (model średniej ruchomej),

Rysunek 4 - układ ARMA

Badamy układ zadając zakłócenia, oraz zakładając znajomość liczby n i m współczynników
odpowiadających za autoregresję (

)

oraz ruchomą średnią (

)

.

System arma opisany jest wzorem:

Estymator przyjmuje postać:

̂ (

)

Dla warunku że (

)

Gdzie



Wektor N wektorów obserwacji wejścia i wyjścia:

[

]

( )



wektor wyjścia systemu estymowanego:

[

]

2. Badania.

Badając działanie ARMY, sprawdzamy wpływ parametrów a i b odpowiedzialnych za człony
AR oraz MA. Wszystkie doświadczenia przeprowadzano z zaszumieniem W kolejnych krokach
sprawdzano:



wyłączone a,



wyłączone b,



duża liczba współczynników a, oraz b,



mała liczba współczynników a, oraz b,



wpływ liczby próbek n.

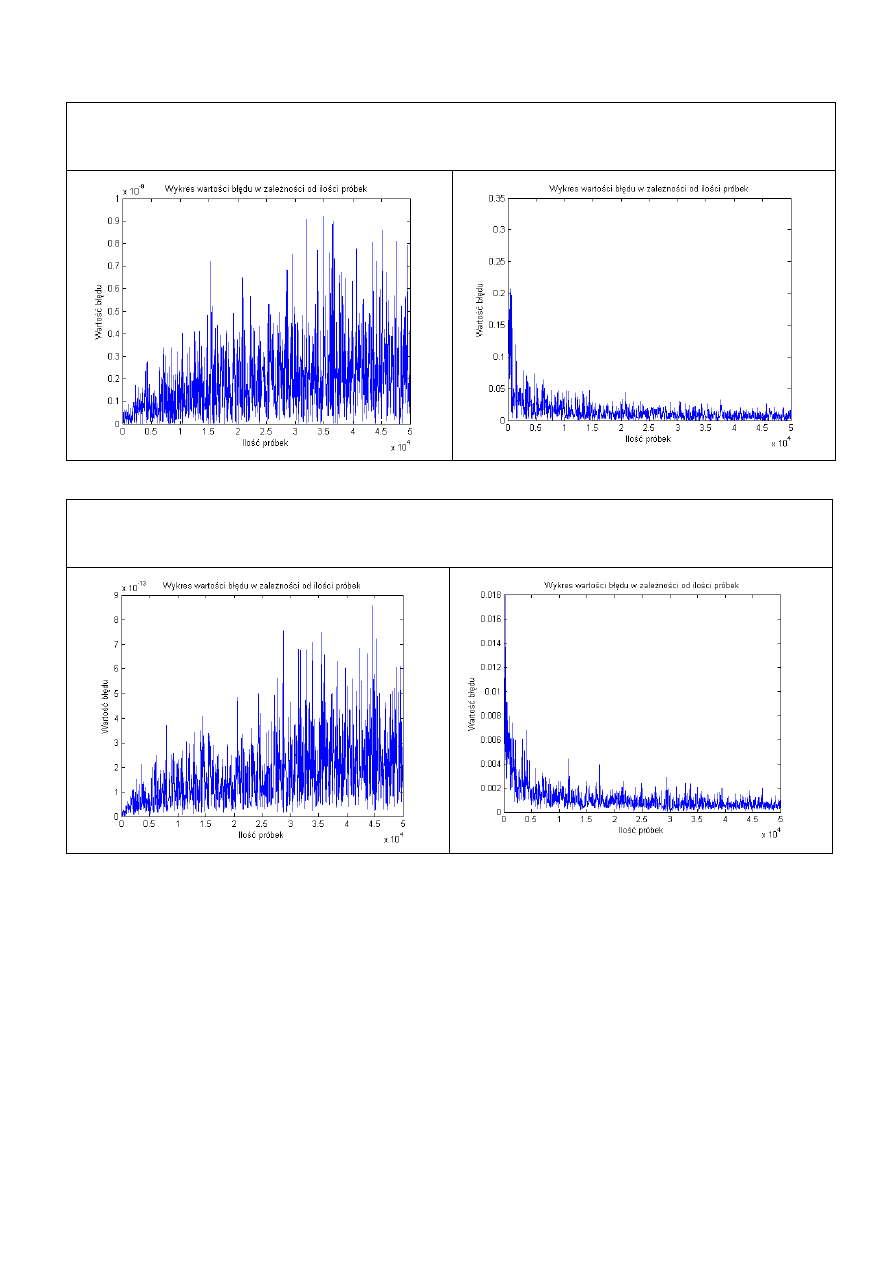
Zgodnie z poprawką ujętą na laboratorium nr 12, w tableli przedstawiono wykres poprawiony
(błąd zbiega do 0), oraz wykres błędny (lab11) gdzie błąd zbiega do ustalonej wartości lub
rozbiega się do nieskończoności.

a=[0.4 0.3 0.2 0.1];

b=[.1 .2 .3];
n=50000

a=[0.4 0.3 0.2 0.1];

b=[.1 .2 .3];
n=50000

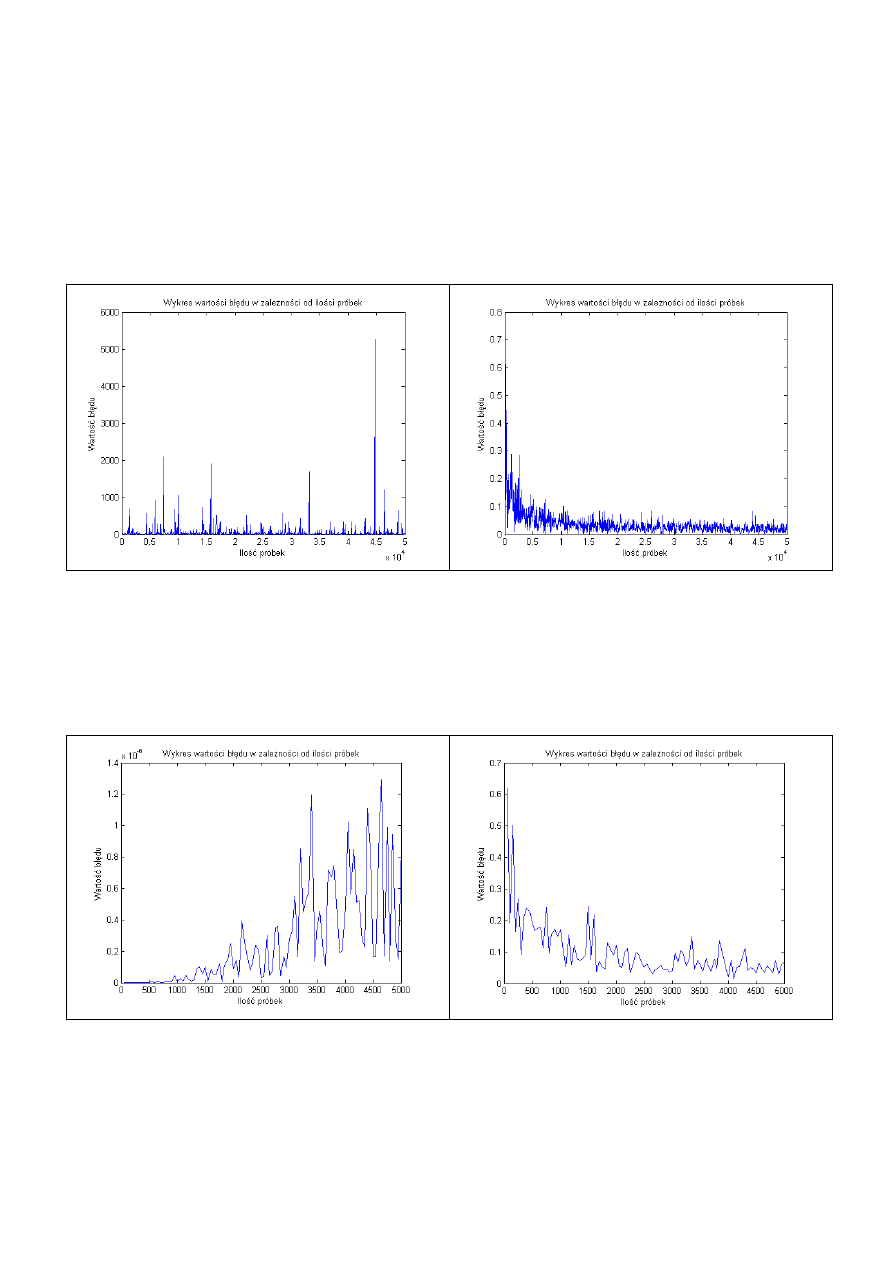
a=[0.001 0.0001]

b=[.1];

a=[0.001 0.0001]

b=[1];

Uwaga.

Podczas badań wpływu parametrów dla wartości (wyłączone a jak i b)

a=[0 0 0 0]

b=[1 0 0];

otrzymano błąd rzędu tysięcy co jest całkowicie niedopuszczalne, wersja poprawiona radzi
sobie jednak z tymi parametrami (można przypuszczać że jest to losowy przypadek gdyż
wyłączenie parametrów a i b wyłącza praktycznie cały model LTI przez co układ przestaje
być zarazem dynamiczny jak i liniowy). B jako jedynka oznacza wyłączoną średnią a=0
oznacza wyłączoną autoregresje.

dla mniejszej liczby próbek.n=5000

Z wykresów tych widać że liczba próbek n wpływa na jakość estymacji, czyli na podobnej
zasadzie jak w powyższych eksperymentach.

3. Wnioski

Z wykresów można zauważyć że estymacja parametrów poprawionej wersji jest poprawna,
wartość błędu przy 1000 próbek jest już satysfakcjonująca, jednak skrypt przed poprawką
pokazuje że wartość błędu rośnie wraz z ilością próbek. Są to nieznaczne wartość (prawie =0)
rzędu

, jednak rozbiegają się do nieskończoności.

Z wykresów widać również że dobór parametrów a i b nieznacznie wpływa na wartości
błędów.

Samo działanie algorytmu symulującego model ARMA jest trudne w implementacji z
wykorzystaniem programu symulacyjnego Matlab. Poprawka nadana algorytmowi na
laboratorium 12 pozwoliła na zbieganie wartości błędu do 0.

Z otrzymanych wyników oraz wiedzy z laboratorium można twierdzić że wykresy otrzymywane
w eksperymencie zwracają poprawne dane.