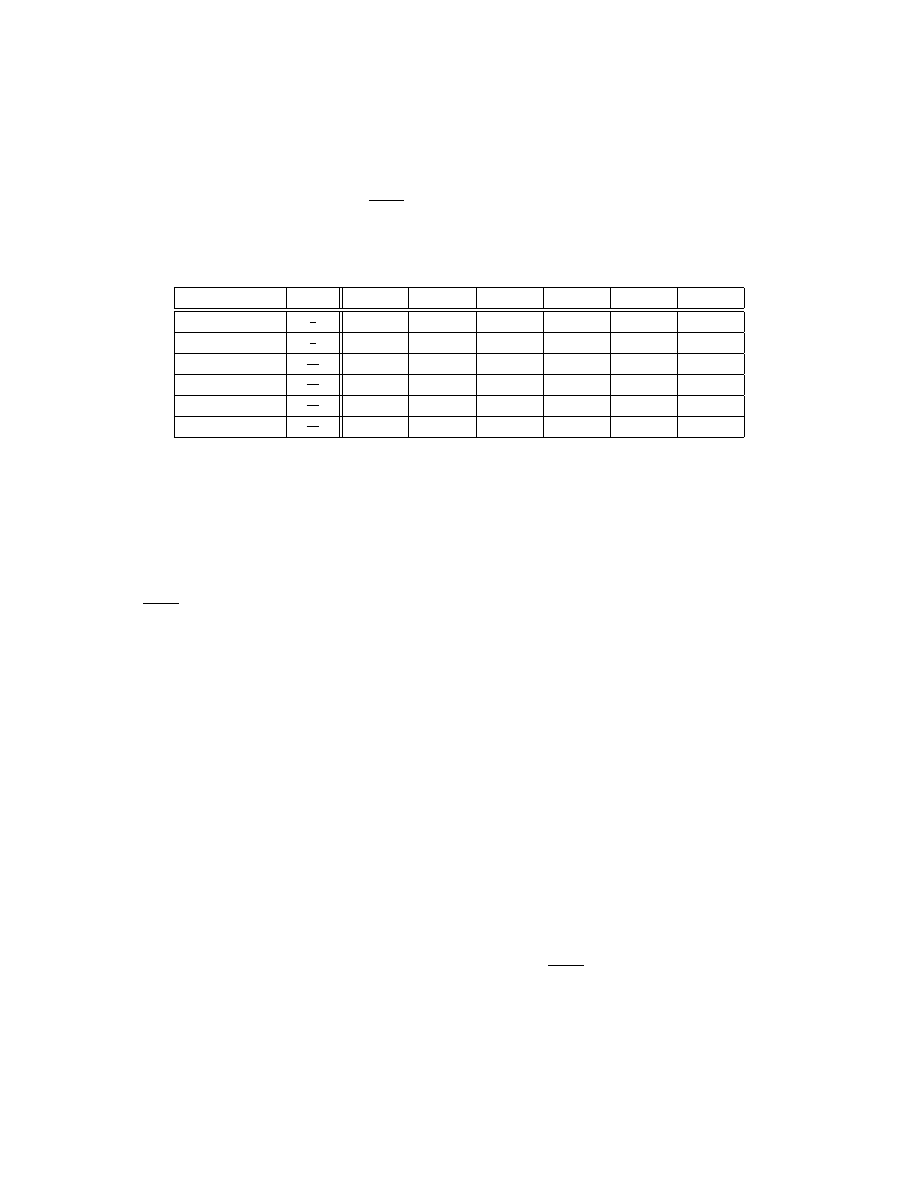
Teoria informacji
i kodowanie

Ćwiczenia III

18. marca 2011 r.

Kodowanie zródłowe, długość słowa kodowego, kod Huffmana, kompresja

Zadanie 1

Ile najwięcej słów kodowych może liczyć binarny jednoznacznie dekodowalny kod, którego naj-
dłuższe słowo ma siedem liter? (Odp. 128)

Zadanie 2

Zbiór sześciu wiadomości x

1

, . . . , x

i

, . . . , x

6

zakodowano według sześciu różnych kodów A − F

podanych w poniższej tabeli:

Wiadomość

p(x

i

)

Kod A

Kod B

Kod C

Kod D

Kod E

Kod F

x

1

1
2

000

0

0

0

0

1

x

2

1
4

001

01

10

10

10

100

x

3

1

16

010

011

110

110

1100

101

x

4

1

16

011

0111

1110

1110

1011

110

x

5

1

16

100

01111

11110

1011

1110

111

x

6

1

16

101

011111

111110

1101

1111

001

Określ, które z podanych kodów są jednoznacznie dekodowalne. Policz średnią długość dla
każdego kodu jednoznacznie dekodowalnego.

Zadanie 3

Źródło generuje równoprawdopodobne 4-symbolowe słowa kodowe kodu zwięzłego trójsymbo-
lowego. Policz, ile maksymalnie informacji o źródle można uzyskać po odebraniu ośmiu słów.
(Odp. 50 bit)

Zadanie 4

Załóżmy, że alfabet kodu liczy D elementów oraz że sekwencja n liczb całkowitych l

i

o nastę-

pującej charakterystyce:

1 ¬ l

1

¬ · · · ¬ l

n

,

spełnia nierówność McMillana-Krafta. Na ile sposobów można wybrać słowa kodowe w

1

, . . . , w

n

o długościach l(w

i

) = l

i

, tak żeby zbiór tych słów kodowych mógł posłużyć do utworzenia kodu

jednoznacznie dekodowalnego?

Zadanie 5

Czy można w alfabecie liczącym trzy elementy skonstruować kod jednoznacznie dekodowalny,
jeśli długości słów kodowych miałyby wynosić:

1, 2, 2, 2, 2, 2, 3, 3, 3, 3?

A jeśli długości słów kodowych miałyby wynosić:

1, 2, 2, 2, 2, 2, 3, 3, 3?

Jak wiele takich kodów (różnych) można skonstruować? (Odp. 6531840)

Zadanie 6

Udowodnij że dla każdego kodu zwięzłego dla źródła o rozkładzie prawdopodobieństwa (p

i

)

zachodzi następująca zależność między prawdopodobieństwami wystąpienia wiadomości a dłu-
gościami reprezentujących je słów kodowych l

i

:

p

j

> p

k

⇒ l

j

¬ l

k

.

Strona 1 z 4

Teoria informacji
i kodowanie

Ćwiczenia III

18. marca 2011 r.

Zadanie 7

Źródło generuje trzy wiadomości z prawdopodobieństwami: p

1

­ p

2

­ p

3

. Pokaż że średnia

długość binarnego kodu Huffmana C dla tego źródła wynosi:

L(C) = 2 − p

1

.

Ile będzie wynosiła średnia długość słowa takiego kodu dla źródła generującego cztery wiado-
mości z prawdopodobieństwami: p

1

­ p

2

­ p

3

­ p

4

?

Zadanie 8

Zakoduj w binarnym kodzie Shannona-Fano zbiór dziesięciu jednakowo prawdopodobnych wia-
domości. Wykaż, że jest to kod zwięzły.

Zadanie 9

(kolokwium z lat poprzednich)

Źródło emituje znaki binarne z prawdopodobieństwem: Pr{0} = p, Pr{1} = 1 − p. Dla ce-
lów transmisji chcemy zastosować następujący kod: 1 → 1000, 01 → 1001, 001 → 1010, . . . ,
00000001 → 1111, 00000000 → 0; tzn. jeśli źródło wyemituje na raz mniej niż 8 zer przed wy-
emitowaniem jedynki, wysyłamy słowo kodowe o postaci 1e

1

e

2

e

3

, gdzie e

1

e

2

e

3

stanowi binarną

reprezentację liczby zer, natomiast gdy wystąpi na raz 8 zer, taką sekwencję reprezentuje się za
pomocą słowa 0. Jako zdarzenie zdefinujemy wygenerowanie słowa kodowego. Czy otrzymany
kod jest kodem jednoznacznie dekodowalnym? Znajdź A

c

: wartość średnią liczby bitów słowa

kodowego na zdarzenie. Znajdź A

s

: wartość średnią liczby bitów wygenerowanych przez źródło

wiadomości na zdarzenie. Wartości średnie są rozumiane probabilistycznie.
Dla p = 0,9 porównaj

A

c

/

A

s

ze średnią długością słowa kodowego na symbol źródła w binarnym

kodowaniu Huffmana czwartego rozszerzenia oryginalnego źródła. Co nam to mówi o optymal-
ności kodowania Huffmana?

Zadanie 10

(kolokwium z lat poprzednich)

Źródło S generuje wiadomości z prawdopodobieństwami 0,3; 0,3; 0,2 i 0,2. Ile istnieje binarnych
kodów zwięzłych dla tego źródła? Ile z nich to kody Huffmana? (Odp. 24 kody, z czego 8 to
kody Huffmana)

Zadanie 11

(kolokwium z lat poprzednich)

Źródło X generuje wiadomości x

1

, x

2

, . . . , x

n

z prawdopodobieństwami p

1

­ p

2

­ · · · ­ p

n

oraz

dodatkowo:

∀

i=1,...,n−3:

p

i

> p

i+2

+ · · · + p

n

.

Pokaż, jakie będą długości słów kodowych dla dowolnego binarnego kodu Huffmana tego źródła.
Ile istnieje różnych binarnych kodów Huffmana dla tego źródła?
Podaj dla każdego n ­ 1 ogólny przykład rozkładu prawdopodobieństwa (p

i

) spełniającego

podane nierówności.

Zadanie 12

Algorytm Huffmana polega między innymi na tworzeniu ciągu zredukowanych źródeł wiadomo-
ści w taki sposób, że za każdym razem (tzn. na etapie redukcji numer i) musimy obliczać praw-

dopodobieństwo p

(i)
Σ

pewnej liczby najmniej prawdopodobnych wiadomości. Pokaż, że średnią

długość binarnego kodu Huffmana C można obliczyć jako:

L(C) = 1 +

X

i

p

(i)
Σ

.

Strona 2 z 4

Teoria informacji
i kodowanie

Ćwiczenia III

18. marca 2011 r.

Zadanie 13

Na podstawie analizy kodowania Huffmana dla bezpamięciowego źródła generującego N ­ 2
wiadomości, pokaż że tworzone w alfabecie binarnym słowa kodowe o długościach l

i

spełniają

nierówność:

N

X

i=1

l

i

¬

1

2

N

2

+ N − 2

.

Zadanie 14

Zaproponuj algorytm definiujący D-arny kod Huffmana C, który nie tylko minimalizuje średnią
długość kodu:

L(C) =

X

i

p

i

l

i

,

ale także minimalizuje całkowitą długość kodu, rozumianą jako:

σ(C) =

X

i

l

i

.

Zadanie 15

Na podstawie analizy kodowania Huffmana (lub korzystając z wyników zad. 14) pokaż, że dla
bezpamięciowego źródła generującego N wiadomości, słowa kodowe binarnego kodu zwięzłego
o długościach l

i

spełniają poniższą nierówność:

N

X

i=1

l

i

­ N lg N.

Zadanie 16

(kolokwium z lat poprzednich)

Pewne źródło generuje losowo wiadomości ze zbioru: x

1

, x

2

, x

3

, x

4

, a następnie przesyła je przy

użyciu zwięzłego binarnego kodu jednoznacznie dekodowalnego (impuls trwa 5 µs każdy). Oblicz
maksymalną szybkość przesyłania słów kodowych (w jednostkach: [

słów kod.

/

s

]), jeśli:

a) Pr{x

i

} = Pr{x

j

} : i, j = 1, 2, 3, 4,

b) Pr{x

1

} = 0,5, Pr{x

2

} = 0,25, Pr{x

3

} = Pr{x

4

}.

Zadanie 17

(kolokwium z lat poprzednich)

Źródło generuje osiem wiadomości elementarnych według następującego rozkładu prawdopo-
dobieństwa:

Pr{x

1

} =

2

5

; Pr{x

2

} =

1

5

; Pr{x

3

} = Pr{x

4

} =

1

10

; Pr{x

5

} = Pr{x

6

} = Pr{x

7

} = Pr{x

8

}.

Znajdź:

a) jednoznacznie dekodowalny kod zwięzły dla tego źródła, gdy alfabet kodu to: {∗, ⊗, •, 4};

b) zbiór list długości ciągów kodowych dla wszystkich kodów zwięzłych jednoznacznie deko-

dowalnych tego źródła dla wszystkich możliwych długości używanych alfabetów.

Zadanie 18

(kolokwium z lat poprzednich)

Mamy bezpamięciowe źródło wiadomości:

"

m

1

m

2

m

3

m

4

m

5

m

6

m

7

m

8

0,03

0,16

0,11

0,31

0,07

0,07

0,19

0,06

#

.

Strona 3 z 4

Teoria informacji
i kodowanie

Ćwiczenia III

18. marca 2011 r.

Zakoduj wiadomości pochodzące z tego źródła kodem jednoznacznie dekodowalnym w taki spo-
sób, żeby zminimalizować średni czas nadawania zakodowanej wiadomości, jeśli alfabet składa
się z trzech liter: a, b, c. Czasy nadawania poszczególnych liter wynoszą: a — 3 sekundy, b — 2
sekundy oraz c — 3 sekundy.

Zadanie 19

(kolokwium z lat poprzednich)

Nasz kolega rzuca w ukryciu parą rozróżnialnych kostek sześciennych, przy czym po każdym
rzucie informuje nas o iloczynie wyrzuconych oczek. Wymyślił sobie, że będzie stosował w tym
celu jednakowej długości ciągi binarne (rozumiemy, co kryje się pod określonymi ciągami, bo
powiedział nam to wcześniej). Jaki jest nadmiar stosowanego przez niego kodu, jeśli wybrał
najkrótszą możliwą długość ciągów i ile średnio symboli mógłby zaoszczędzić przy podawaniu
wyników 1000 rzutów, gdyby wybrał najlepszy możliwy dla tej sytuacji kod?

Zadanie 20

Znajdź entropię źródła X, które generuje nieskończenie wiele wiadomości m

1

, m

2

, . . . , m

i

, . . .

(zbiór wiadomości jest równoliczny ze zbiorem liczb naturalnych) o prawdopodobieństwie:

p

i

= 2

−i

(i = 1, 2, 3, . . . ).

Znajdź optymalny binarny kod jednoznacznie dekodowalny i oblicz jego średnią długość. (Odp.
2

bit

/

wiadom.

)

Zadanie 21

(**)

Teorię informacji (w szczególności zwięzłe kodowanie źródłowe) można użyć do zaprojektowa-
nia efektywnych testów przesiewowych krwi. Załóżmy, że mamy do przebadania pod kątem
obecności wirusa N próbek krwi. Prawodopodobieństwo pozytywnego wyniku (czyli wykrycia
wirusa) dla każdej próbki jest niewielkie (p = 0,01), a testy są kosztowne, więc trzeba minima-
lizować ich liczbę. Zamiast badać każdą próbkę z osobna, można badać zmieszane fragmenty
próbek. Zakładamy wtedy, że wynik będzie pozytywny, jeśli choć jedna z wymieszanych próbek
zawierała wirusa. Zakładamy też, że każdą próbkę można podzielić na dowolnie wiele fragmen-
tów. Ostatecznie musimy jednak dla każdej próbki wiedzieć czy na pewno zawiera wirusa czy
nie. Jak maksymalnie zmniejszyć oczekiwaną liczbę testów do wykonania? Zaprojektuj badanie
dla 300 próbek i podaj oczekiwaną liczbę testów.

Informacja dodatkowa:
Na kartkach z zadaniami do kolejnych kolokwiów znajdą Państwo następujące dane:

„Legalna ściąga”:

H(X, Y ) = H(X) + H(Y |X) (reguła łańcuchowa)

I(X; Y ) = H(X) − H(X|Y ) = H(Y ) − H(Y |X) = H(X) + H(Y ) − H(X, Y )

X, Y — niezależne: H(X, Y ) = H(X) + H(Y )

Strona 4 z 4