Teoria informacji i kodowanie:
ćwiczenia I
Informacja, niepewność, entropia
Piotr Chołda
Katedra Telekomunikacji Akademii Górniczo-Hutniczej
Kraków, 4. marca 2011 r.
Teoria informacji i kodowanie:
ćwiczenia I
Informacja, niepewność, entropia
Piotr Chołda
Katedra Telekomunikacji Akademii Górniczo-Hutniczej
Kraków, 4. marca 2011 r.
Kontakt z prowadzącym
Dr inż. Piotr Chołda
I
015, parter pawilonu D5
U
Czwartek, 15.30-17.00
(ale można spotkać się też o innej porze;
tylko wcześniej proszę o e-maila)
T
(617–)40–36
B
m
TIiK: ćwiczenia
2/32
Zasady zaliczenia
Zaliczenie w normalnym trybie
Cztery kolokwia
Zakaz używania kalkulatorów i wszelkich innych
„wspomagaczy”
Dwa zadania (jedno za 12, drugie za 13 punktów)
Nieobecność: 0 punktów. Nie ma poprawek
Preferowana opcja:
kolokwia dla całego roku na raz
Aktywność podczas zajęć: punktowana pojedynczymi
punktami; nie ma punktów ujemnych
,
Ustalamy: do tablicy—tylko
chętni
(póki są. . . )
Wśród zadań domowych czasem są „zadania dla ambitnych”
— pierwsza osoba, która wyśle poprawne rozwiązanie takiego
zadania dostanie dodatkowe punkty
Ocena końcowa jest liczona według Regulaminu Studiów,
§13.1-2
TIiK: ćwiczenia
3/32
Zasady zaliczenia
Nieobecność i kolokwia zaliczeniowe
Regulamin, §11.3: obecność na ćwiczeniach jest obowiązkowa
Dopuszczalne są co najwyżej
dwie
nieobecności
nieusprawiedliwone
Student, który opuści bez usprawiedliwienia większą liczbę
zajęć — nie może zdawać kolokwiów poprawkowych!
(Regulamin, §15.3)
Pozostali studenci uczęszczający na zajęcia i bez zaliczeń:
mają prawo zdawać dwa kolokwia poprawkowe (aż uzyskają
ocenę
dostateczną
)
Niezadowoleni z oceny pozytywnej: zaliczenie w trybie
komisyjnym
Zgodnie z Regulaminem Studiów, §16.1, do egzaminu można
przystępować
pod warunkiem
uzyskania zaliczenia z ćwiczeń
(
żadna
inna opcja nie jest przewidywana)!
TIiK: ćwiczenia
4/32
Program ćwiczeń w roku 2010/2011
2
11. marca: Źródła informacji, kanały transmisyjne, przepustowość
3
18. marca: Kodowanie źródłowe, długość słowa kodowego, kod Huffmana,
kompresja, kodowanie arytmetyczne, adaptacyjny kod Huffmana
4
około 25 marca (7 kwietnia?):
Kolokwium I
— entropia, kodowanie źródłowe
5
1. kwietnia: Kody nadmiarowe, odległość Hamminga, kresy
6
8. kwietnia: Kody liniowe, kody Hamminga
7
około 15. kwietnia (5 maja?):
Kolokwium II
— kody nadmiarowe, kody
Hamminga
8
6. maja: Zaawansowane kody liniowe (modyfikacje, kody iteracyjne. . . )
9
13. lub 20. maja: Kody wielomianowe (wstęp)
10
27. maja: Kody cykliczne
11
około 3-10. czerwca (17 czerwca?):
Kolokwium III
— rozbudowane kody
liniowe (modyfikacje, kody wielomianowe. . . )
12
17. czerwca: Kody splotowe (wstęp)
13
22. czerwca,
środa
: Dekodowanie kodów splotowych
14
24. czerwca:
Kolokwium IV
— kody splotowe
15
1. lipca, 9.00,
nie ulegnie zmianie
:
Kolokwium zaliczeniowe poprawkowe I
16
8. lipca, 9.00,
nie ulegnie zmianie
:
Kolokwium zaliczeniowe poprawkowe II
TIiK: ćwiczenia
5/32
Materiał do powtórzenia/dorobienia
Analiza:
Właściwości funkcji logarytm
Dwumian Newtona
Ciągi i ich sumy
Metody obliczania sum szeregów
Rachunek prawdopodobieństwa:
Prawdopodobieństwo warunkowe (w tym tw. Bayesa)
Dyskretne rozkłady prawdopodobieństwa (m.in. rozkład
Bernoulliego, rozkład dwumianowy)
Zmienne losowe (również dwuwymiarowe oraz funkcje zmiennej
losowej)
Wartość oczekiwana/średnia zmiennej losowej i jej wlaściwosci
(np. w. ocz. sumy zmiennych)
Procesy losowe i łańcuchy Markowa
TIiK: ćwiczenia
6/32
Literatura do ćwiczeń
Polecam trzy, stosunkowo nowe pozycje w języku polskim:
Podstawy rachunku prawdopodobieństwa: Agnieszka
Plucińska, Edmund Pluciński, Probabilistyka.
Warszawa:
Wydawnictwa Naukowo-Techniczne, 2000.
Zadania z TIiK: Jan Chojcan, Jerzy Rutkowski, Zbiór zadań z
teorii informacji i kodowania.
Gliwice: Wydawnictwo
Politechniki Śląskiej, 1994.
Zadania z TIiK: Radosław Biernacki, Bohdan Butkiewicz,
Jerzy Szabatin, Bożena Świdzińska, Zbiór zadań z teorii
sygnałów i teorii informacji.
Warszawa: Wydawnictwo
Politechniki Warszawskiej, 2007.
TIiK: ćwiczenia
7/32
Miara informacji
Zawartość informacyjna pojedynczej wiadomości
Jeśli pewna wiadomość x
i
może wystąpić z prawdopodobieństwem
Pr{x
i
} = p
, to jej zawartość informacyjna wynosi:
I (x
i
) = I (p) = lg
1
p
= − lg p
Na przykład:
I
1
10
≈ 3, 32
I
1
2
= 1
I
9
10
≈ 0, 15
TIiK: ćwiczenia
8/32
Miara informacji cd.
Entropia zmiennej losowej
Zmienna losowa
X
o
dyskretnym
rozkładzie prawdopodobieństwa
Pr{X = x
i
} = Pr{x
i
} = p
i
(
P
i
p
i
= 1) charakteryzuje się
entropią
(zmiennej losowej)
, którą można rozumieć jako wartość średnią
zawartości informacyjnej:
H(X ) = H(p
1
, p
2
, . . . ) = −
P
i
p
i
lg p
i
[
bitów
/
wiadomość
]
Źródło informacji zazwyczaj utożsamiamy z jakimś rozkładem
zmiennej losowej.
TIiK: ćwiczenia
9/32
Kilka użytecznych konwencji. . .
Umówmy się na oznaczenia:
log
2
= lg
log
10
= log
log
e
= ln
Gdy wiadomo lub nie jest istotne, jaki przedział przebiega
zmienna indeksująca i , często dla wygody zapisujemy:
P
i
(
P
i
) zamiast np.
N
P
i =0
. Ale gdy przebieg zmiennej indeksującej
jest „nietypowy” lub szczególnie ważny z punktu widzenia
danego problemu, zapisujemy dokładniej, np.
K −5
P
i =N+2
TIiK: ćwiczenia
10/32
Właściowości entropii
Niech będzie dany dyskretny rozkład prawdopodobieństwa
zmiennej losowej X , której zbiór realizacji ma liczność N (możemy
ten rozkład utożsamić z rozkładem prawdopodobieństwa
generowania wiadomości przez jakieś źródło wiadomości).
Granica dla zerowych prawdopodobieństw
lim
p→0
p × lg p = 0
Ograniczenie górne i dolne
0 ≤ H(X ) ≤ lg N
Równomierny rozkład prawdopodobieństwa
dla rozkładu
Pr{X = x
i
} =
1
N
, 1 ≤ i ≤ N, entropia osiąga
maksimum po wszystkich rozkładach
N-elementowych:
H
max
(X ) = H
1
N
,
1
N
, . . . ,
1
N
= lg N
TIiK: ćwiczenia
11/32
Rozszerzenie źródła
k-krotne rozszerzenie źródła
Niech będzie dane dyskretne źródło X , generujące N wiadomości
x
1
, x
2
, . . . , x
N
. Weźmy sekwencje o długości k złożone z
wiadomości generowanych przez X :
s
i
= x
i (1)
x
i (2)
. . . x
i (k)
.
Źródło generujące wiadomości s
i
nazywamy
k-krotnym
rozszerzeniem źródła
.
Jeśli X
k
jest k-krotnym rozszerzeniem
bezpamięciowego
źródła X ,
wtedy:
H X
k
= k × H(X )
TIiK: ćwiczenia
12/32
Zadanie powtórzeniowe I
Policzmy sobie entropie różnych zmiennych losowych. . .
Która z poniższych sekwencji niesie większą informację:
1
10 liter alfabetu łacińskiego (zakładamy, że wystąpienie każdej
z 32 liter jest równie prawdopodobne, nie interesuje nas
rozróżnienie między wielkimi a małymi literami),
2
32 cyfry (zakładamy, że wystąpienie każdej z dziesięciu cyfr
jest równoprawdopodobne)?
TIiK: ćwiczenia
13/32
Zadanie powtórzeniowe II
Wyprowadźmy sobie właściwość dla entropii maksymalnej. . .
Używając właściwości logarytmu naturalnego:
ln x =
x − 1,
gdy x = 1
y < x − 1,
gdy x 6= 1
udowodnij następujące twierdzenie:
Jeśli źródło generuje N ≥ 1 wiadomości (1, . . . , N), każdą z
prawdopodobieństwem odpowiednio p
i
, to entropia tego źródła
charakteryzuje się poniższą właściwością:
H(X ) = H (p
1
, p
2
, . . . , p
N
) ≤ lg N,
przy czym równość zachodzi wtedy i tylko wtedy gdy ∀
i
p
i
=
1
N
.
TIiK: ćwiczenia
14/32
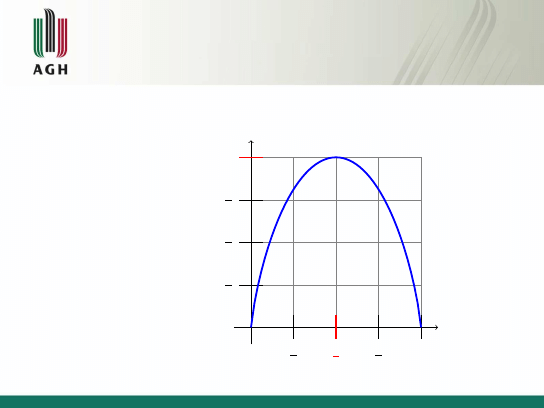
Właściowości entropii cd.
Entropia binarnego źródła wiadomości
p
H(p, 1 − p) = −p × lg p − (1 − p) × lg(1 − p)
1
4
3
4
1
1
2
1
4
1
2
3
4
1
TIiK: ćwiczenia
15/32
Entropia dla wielu zmiennych losowych
Entropia łączna
Entropia łączna
Dla dwóch dowolnych zmiennych losowych X , Y o łącznym
rozkładzie prawdopodobieństwa
Pr {X = x
i
, Y = y
j
} = Pr {x
i
∩ y
j
} = Pr {x
i
, y
j
} = p(i , j) = p
ij
(
P
i
P
j
p(i , j ) = 1) następująco definiujemy
entropię łączną
:
H(X , Y ) = −
P
i
P
j
p(i , j ) lg p(i , j )
Przypomnijmy sobie przy okazji użyteczne właściwości:
Pr {x
i
} =
P
j
Pr {x
i
, y
j
}
Pr {x
i
|y
j
} =
Pr
{
x
i
,y
j
}
Pr
{
y
j
}
X , Y — zm. los. niezależne: Pr {x
i
, y
j
} = Pr {x
j
} × Pr {y
j
}
TIiK: ćwiczenia
16/32
Zadanie powtórzeniowe III
Przydatna właściowość entropii łącznej
Pokaż, że dla niezależnych zmiennych losowych X , Y entropia
łączna wynosi:
H(X , Y ) = H(X ) + H(Y ).
TIiK: ćwiczenia
17/32
Entropia dla wielu zmiennych losowych
Entropia warunkowa
Entropia warunkowa
Dla połączonych doświadczeń (zmiennych losowych) X i Y
entropia warunkowa H(Y |X )
jest definiowana jako wartość średnia
entropii Y pod warunkiem znanej realizacji zmiennej X :
H(Y |X ) = −
P
i
Pr{x
i
}
P
j
Pr{y
j
|x
i
} × lg Pr{y
j
|x
i
} =
= −
P
i
P
j
Pr{x
i
, y
j
} × lg Pr{y
j
|x
i
}
Entropia warunkowa służy do oceny ilościowej naszej niepewności
odnośnie do Y przy znanym wyniku X .
TIiK: ćwiczenia
18/32
Zadanie powtórzeniowe IV
Użyteczna właściowość entropii łącznej
Udowodnij następującą właściwość (tzw.
reguła łańcuchowa
):
H(X , Y ) = H(X ) + H(Y |X ).
TIiK: ćwiczenia
19/32
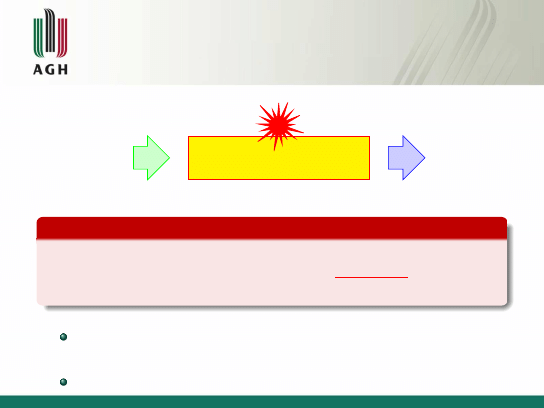
Informacja wzajemna (transinformacja)
x
1
..
.
x
M
X
Kanał informacyjny
y
1
..
.
y
L
Y
Informacja wzajemna
Informację wzajemną
(
transinformację
) definiujemy następująco:
I (X ; Y ) =
P
i
P
j
Pr{x
i
, y
j
} lg
Pr{x
i
,y
j
}
Pr{x
i
} Pr{y
j
}
Piszemy średnik I (X
;
Y ), a nie przecinek (czasem stosowany
zapis I (X
,
Y ) oznacza coś innego!)
We wzorze definicyjnym
nie ma
minusa!
TIiK: ćwiczenia
20/32
Informacja wzajemna cd.
Właściwości
Poniższe właściowości pokazują, dlaczego tak zdefiniowana
transinformacja, jest użyteczna w transmisji danych:
I (X ; Y ) = I (Y ; X )
I (X ; Y ) = H(X ) − H(X |Y )
I (X ; Y ) = H(Y ) − H(Y |X )
I (X ; Y ) = H(X ) + H(Y ) − H(X , Y )
TIiK: ćwiczenia
21/32
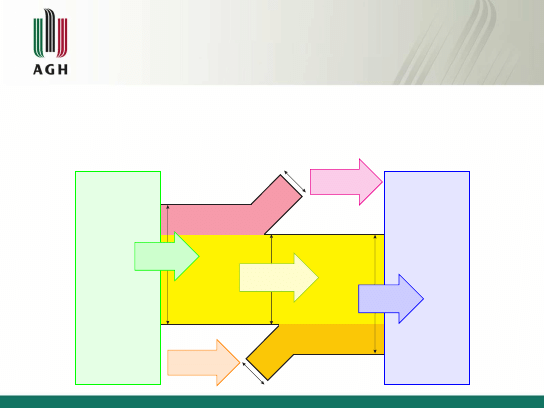
Informacja wzajemna cd.
Interpretacja graficzna dla kanału transmisyjnego
Proszę pamiętać, że „kanał informacyjny” to bardzo szerokie
pojęcie (kanał transmisyjny, urządzenie magazynujące,
skompresowany plik. . . )
Nadajnik
X
H(X )
Entropia
wejściowa
I (X ; Y )
Transinformacja
Utrata informacji
H(X |Y )
Szum informacyjny
H(Y |X )
Odbiornik
Y
H(Y )
Entropia
wyjściowa
TIiK: ćwiczenia
22/32
Zadanie powtórzeniowe V
No to udowodnijmy sobie, że tak jest. . .
Udowodnij że dla transinformacji zachodzą poniższe tożsamości:
I (X ; Y ) = I (Y ; X )
= H(X ) − H(X |Y )
= H(Y ) − H(Y |X )
= H(X ) + H(Y ) − H(X , Y )
TIiK: ćwiczenia
23/32
Użyteczne wzory na kolokwium
Pewne użyteczne zależności będą w poniższej formie zapisane na
kartce z kolokwium (więc nie trzeba się ich uczyć na pamięć,
ale
trzeba je rozumieć!):
H(X , Y ) = H(X ) + H(Y |X )
I (X ; Y ) = H(X ) − H(X |Y )
= H(Y ) − H(Y |X )
= H(X ) + H(Y ) − H(X , Y )
X , Y — niezależne: H(X , Y ) = H(X ) + H(Y )
TIiK: ćwiczenia
24/32
Zadanie 1
Jaką maksymalną nieokreśloność może zawierać fotografia
6 × 9 cm
2
, jeśli rozmiar ziarna jest równy 0, 01 × 0, 01 cm
2
, a każde
ziarno może mieć trzy odcienie: biały, czarny i szary?
TIiK: ćwiczenia
25/32
Zadanie 2
Źródło generuje wiadomości według następującego schematu:
1
losowane są 0 oraz 1 (odpowiednio z prawdopodobieństwem
p
0
= p, p
1
= 1 − p);
2
losowanie kończy się w chwili wylosowania pierwszej jedynki;
3
źródło wysyła informację, za którym razem to nastąpiło.
Znajdź entropię takiego źródła.
TIiK: ćwiczenia
26/32
Zadanie 3
Pokaż, że źródło informacji X generujące wiadomości
x
0
, x
2
, . . . , x
N
zgodnie z rozkładem dwumianowym (rozkładem
Bernoulliego), tj. dla 0 ≤ k ≤ N, 0 < p < 1 oraz q = 1 − p:
Pr{X = x
i
} =
N
i
p
i
q
N−i
,
charakteryzuje się entropią:
H(X ) ≤ −N(p log
2
p + q log
2
q).
TIiK: ćwiczenia
27/32
Zadanie 4
Kolokwium z lat poprzednich. . .
Źródło Z jest zdefiniowane w sposób następujący:
1
mamy dwa źródła X i Y o entropiach odpowiednio H(X ) i
H(Y );
2
wiadomości generowane przez te źródła nie pokrywają się (np.
jedno generuje litery, a drugie — cyfry);
3
ze źródła Z wysyłamy informację na tej zasadzie, że z
prawdopodobieństwem p podajemy na jego wyjście wiadomość
ze źródła X , a z prawdopodobieństwem (1 − p) — wiadomość
ze źródła Y .
Jaka jest entropia Z ?
TIiK: ćwiczenia
28/32
Zadanie 5
Zmienna losowa X przebiega z takim samym
prawdopodobieństwem wartości całkowitoliczbowe 1, 2, . . . , 2N.
Zmienna losowa Y jest zdefiniowana jako równa 0, gdy wartość X
jest parzysta, natomiast Y = 1, gdy wartość X jest nieparzysta.
Udowodnij, że w takim przypadku zachodzi następująca zależność
dla entropii warunkowej:
H(X |Y ) = H(X ) − 1.
A następnie pokaż, że zachodzi również:
H(Y |X ) = 0.
TIiK: ćwiczenia
29/32
Zadanie 6
Kolokwium z lat poprzednich. . .
Dana jest dyskretna zmienna losowa X . Inna zmienna losowa
zdefiniowana jest przez funkcję:
Y = g (X ),
gdzie g (·) jest dowolną funkcją. Jaka zależność ogólna zachodzi
między H(Y ) i H(X ):
H(Y ) ≤ H(X ),
H(Y ) ≥ H(X )?
Przy jakich warunkach nałożonych na funkcję g (·) zachodzi
równość?
TIiK: ćwiczenia
30/32
Zadanie 7
Kolokwium z lat poprzednich. . .
Nasz kolega wykonuje w ukryciu trzy rzuty niesfałszowaną monetą,
po czym mówi nam, ile w sumie wypadło orłów. Jak wiele
informacji na temat wyniku pierwszego rzutu dostarcza nam w ten
sposób?
TIiK: ćwiczenia
31/32
Pytania? Dziękuję za
uwagę! Za tydzień
źródła
wiadomości
,
kanały
transmisyjne
i
obliczanie
przepustowości
—
dokończenie materiału z
wykładu 1
TIiK: ćwiczenia
32/32