!

"

#

!

$

#

#%##

#

!

"

#

#

#

!

"

#

#

#

&%#

!

$

!

#

!

#

Æ

'

#

#

!

$

#

%#

(

)

#

%#!

#

&%

#

*

+

!

%

#

,

-#

#

-

#

#

#

#!

#

# #

#

,

%

#

#

#

!

,

#'

!

#

#

,

#!

.

,

#!

!

/

#

'

#

#

,

%#

&

!

0#

,

-

!

##

1

2

3

&

!

4

#

,

#

!

"

#

#

#

#

!

Æ

#

!

5

##

#

#

-#

#

!

,

#

#

#

#

6

#

#

,

#

*

!

#

#!

"

7

#

#

,

!

/

#

#

#

8

!

# #

#

#

#

#

!

"

#

#!

#

%#

#Æ!

%#

#

%

##

!

#

-

9

Æ

:

(!)

#

9

9

(!*)

#

&

&

(!&)

#

#

#

#

#

#

9

*

(

:

)

9

*

(

)

(!)

#

##

7%

#

#

#

,

#

#!

/#

,

#

7

#

#

##

!

-

#

9

(!+)

#

#

#

#

##

#!

/

# #

9

:

:

:

(!;)

#

#

!

<

9

:

(!2)

/

#

9

:

(!)

#

!

#

<

9

<

9

9

(!8)

$

#%##

¼

9

<

(!3)

#

(

<

)

(

<

)

9

<

<

<

<

9

(

)

<

9

<

(!)

"

,

#

¼

¼

9

<

<

9

9

(!*)

<

#

:

#

!

$

#

#

9

(

*)

(!&)

Tangent plane

$

-#

!

"

#

9

(

=

*)

(!)

9

#

=

9

%

!

#

#

!

6

##

#%

%#

!

$

%#

#

!

#

>

#!

!

/

#

%#!

#

(

5

!)!

$

!

(

)

9

(

*)

(

*)

(

*)

(!+)

6

(!;)

#

#%##

!

"

#

#

#

>

7

&%

#

#

-#!

,

!

R

R

θ

0

1

!

4

#

#

-#

#%

?

@

,

A

@

-

,

#!

#

<

9

3

(!2)

"

-#

#

B #!

CD

#

#-#

()

9

(

)

(!)

(3)

9

()

9

(!8)

"

-#

(

)

9

<

(!*3)

#-#

(

)

!

"

#

#

!

#

9

(

*)

(!*)

#

!

>

,

(

)!

5

#

#

!

#

#

%#

!

(

)

-#

(

5

!*)!

#

()

9

:

=

(!**)

#

9

=

!

6

,

(

)

9

:

=

9

<

(!*&)

"

()

9

:

(

<

)

(!*)

9

(

)

:

(!*+)

-

()

<

()

9

!

#

9

( *)

(

:

)

(!*;)

,

-#

#

!

6

#

#

#Æ

#

!

4

#

#

-#

!

/

!

5

CD

-!

!

"

#'

#

-

!

##

#

!

#

#!

-#

,

#

!

,

%#

#

-#

!

/

#

,

#!

"

#

%

!

#

#-

#!

#

!

#

%

#

7

!

'

%#

#

!

@

,

%

#

#

#

(

E

)

#

#'

!

%

#

#

#

!

#

#

%

!

@

#

>

!

#

#

!

@

-

#

9

:

(!*2)

!

@

#-

9

(!*)

#

# #

!

"

-

9

(!*8)

%#

!

/

#

F1D

#

#!

,

%

<

9

 

(!&3)

,

9

(!&)

9

<

#

9

3

#

9

3!

 

9

 

<

(!&*)

 

9

<

9

(!&&)

(!&3)

#

!

"

%

#

#

!

#

#

!

@

#'

!

(

<

)

9

<

9

 

(!&)

@

 

9

 

:

G

G

 

(!&+)

#

#

#'

(

#'

#)!

@

!

@

#

#

3

9

 

9

 

:

G

G

 

(!&;)

"

G

G

 

9

 

(!&2)

6

-

 

#

#'

!

@

 

G

G

 

9

 

 

(!&)

@

#

#

(!&+)

-#

 

9

 

 

 

(!&8)

"

 

9

 

 

9

*(

<

)

(!3)

#

#

%

!

#

!

#

!

6

%#

>

#

#!

#

#

#

%

#

#!

(!3)

,

%

(

<

)

,

#

!

<

#

!

#

%

#

#

#

#

#

%

#

%

!

H

!

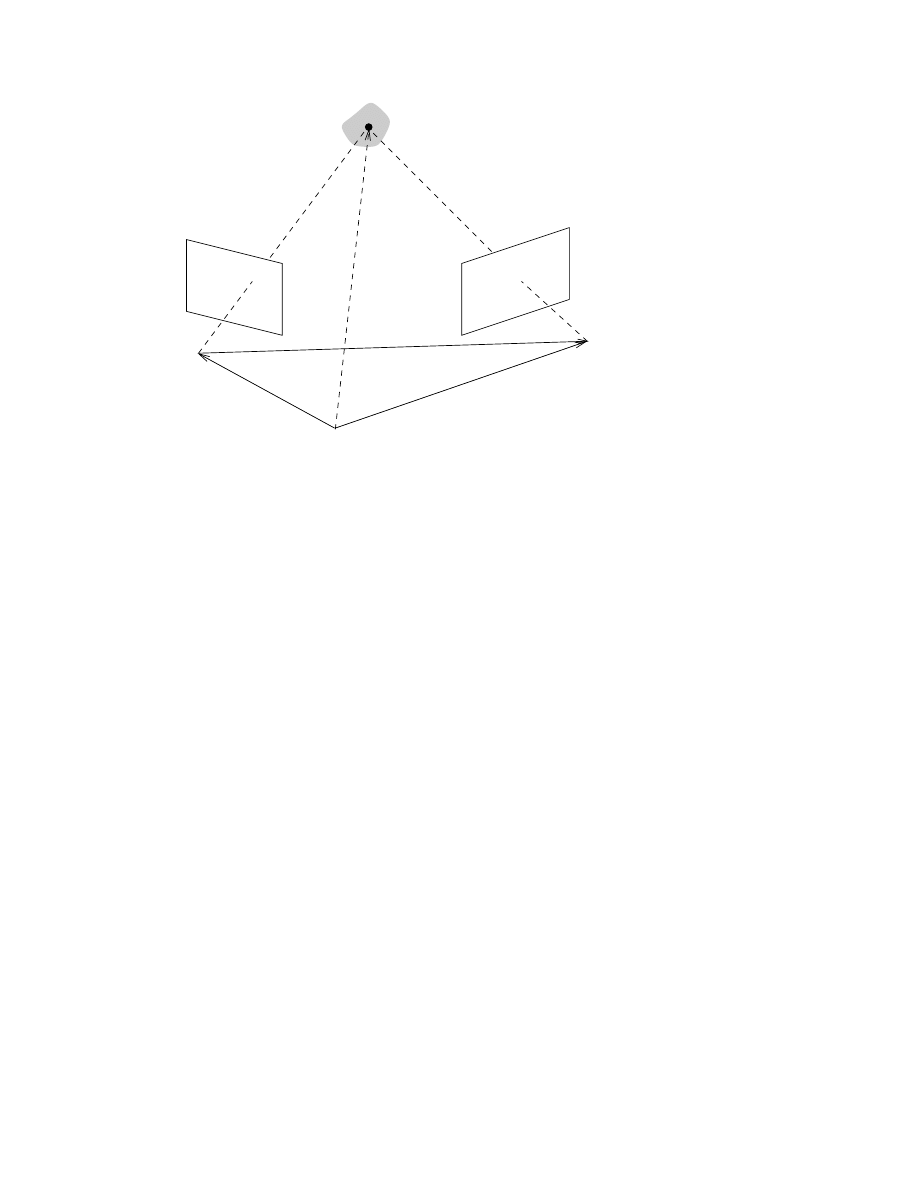
Camera 1

Camera 2

Object

X

t

t

1

2

t

O

"

#

$

%

¾

½

1!

4

#'

!

###

-#

#

%

!

#

,

%#

!

/%

#

#

-#

#

#

!

6

#

7

#

(

4

!;)

-

#

,

!

&%#

#

#

#!

#

6

-#

!

4

,

%#

#

(

)!

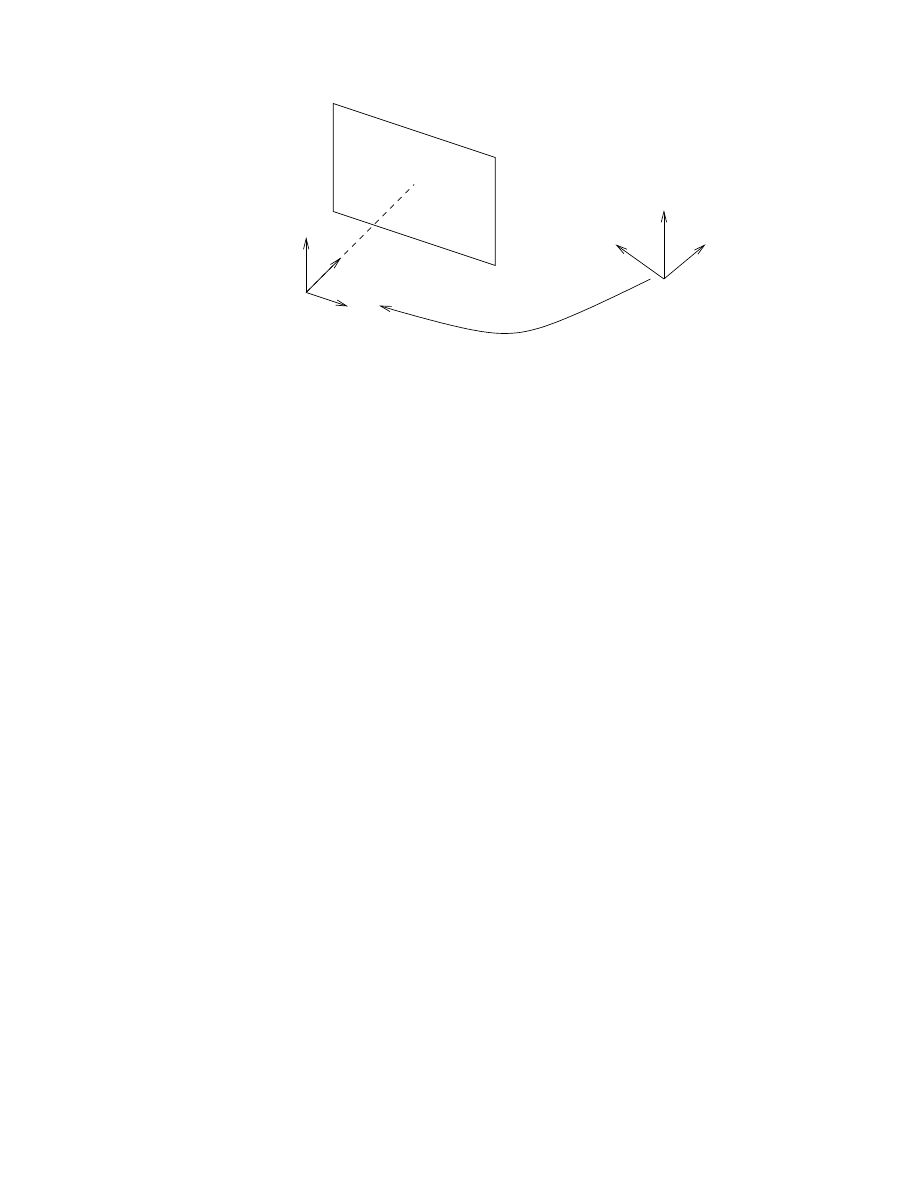
e

3

f

1

f

3

f

2

R

1

e

e

1

Optical

Centre

Camera 1

2

&

"'%

%

(

)

¾

½

!

,

#

##

;

2

!

#

#

#%

#

#

#

#

#

#

6

%

!

$

#

#

#

(

5%

!&)!

#

#

F

#

!

@

##

#

#

!

/

,

#

#

!

"

#

#

#

#

9

(

)

(!)

9

(

)

(!*)

@

#

#

#

9

<

9

<

(!&)

(4

5

!)!

#

,

#

,

#

%

!

#

,

>

#

#

#

!

"

#

#

#

#

!

@

#-

9

9

(!)

#

#

9

<

:

9

<

:

(!+)

!

@

#

%

7

#

#

(

#

#)

%

#

'!

@

##

#

#

!

-

#

!

#

%

#

#

!

#

6

,

(

##)

!

#

!

#

#

( #

)

(

%

)

(

)

*

(

)

(!;)

(

)

*

(

)

(!2)

#

(

)

*

(

<

:

)

(!)

#

!

7

#

(

)

*

(

<

:

)

:

(

<

:

)

(!8)

6

D

*

(

)

9

(

)

(

)

(

)

(

)

(

)

(!+3)

#

#

!

-

(

)

#

#

B

,

#

##

%

#!

"

,

#

#

#

!

@

6

D

#

(

)

(

)

(!+)

!

#

#

#!

#

#

#

#

(

)

!

!

!

(

)

(!+*)

#

(

)

:

(

)

9

*

*

(

:

)

:

*

(

)

(!+&)

/

(

)

*

(

<

<

:

)

(!+)

I

#

#'

"

9

(

<

<

:

)

(!++)

##

;

2

!

-

"

(!++)

#

# #

!

!

"

"

#

9

J

<

J

<

(!+;)

J

9

J

9

(!+2)

#'

#

#

#

# #

!

K

#

,

"

"

"

9

(

J

)

<

(

J

)

<

(!+)

# #

#

"

¼

9

(

J

)

<

(

J

)

<

(!+8)

<

#!

#

#'

"

¼

!

0

(!3)

(

(

J

)

<

)

(

(

J

)

<

)

9

3

(!;3)

,

#

#

9

3

(!;)

9

(

J

)

(

<

(

J

)

<

)

(!;*)

#

%

#

##

!

!

#!

"#

#

(!8)

!

%

(

)

9

:

(

)

(!;&)

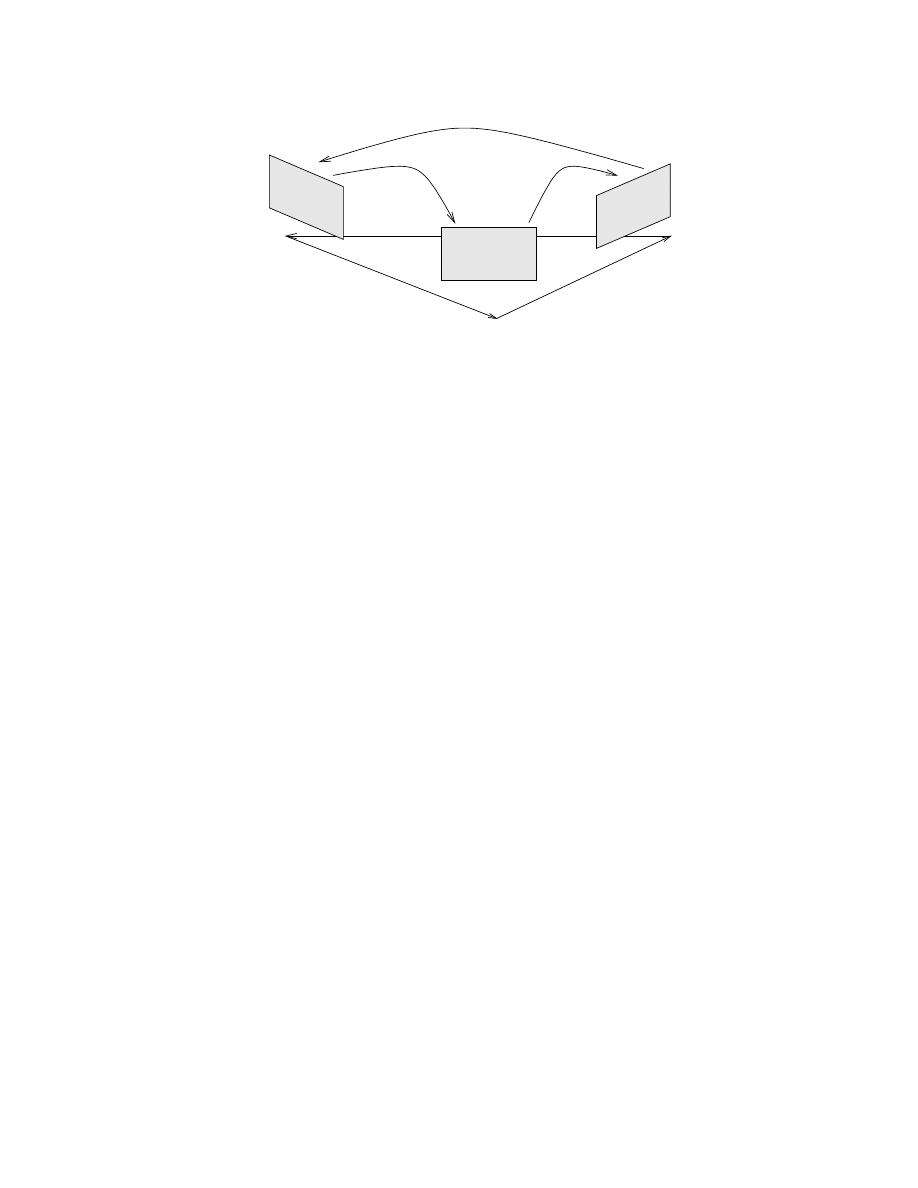
R

12

R

23

t

31

t

23

t

12

Camera 1

Camera 2

Camera 3

R

31

*

½¾

!

¾¿

!

¿½

¿½

¾¿

½¾

(

)*

#'

"

9

(

<

<

:

)

(!;)

#

!

#

#

# #

,

#

!

I

"

9

J

<

J

<

(!;+)

/

:

:

-#!

4

"

"

9

(

J

)

<

(

J

)

<

(!;;)

!

/

#

!

#

(5

!+)!

#

(

J

)

<

(

J

)

<

:

(

J

)

<

9

3

(!;2)

#

(

J

)

<

(

J

)

<

:

(

J

)

<

9

3

(!;)

-

7

-

#

!

/

#

!

#

*%

#

#

%

# !

$

%

%

&

# #

*

# #

!

#

%

#

#

"

(!;;)!

-#

##

#

#

!

"

#

#

#

#

!

"#

#

(

5

!;)!

#

#

(

)

#

!

/#

7

#

#

(

)

!

#

#

9

(#

#

)

#

#

&

&

#

9

(

)

9

 

#

(!;8)

(4

8

#)!

##

,

!

5

7

(

)

#

!

5

*%

5

!&

#

L

9

(

)

(

)

$

9

*

(!23)

/

#

#

#

#

,

#

#

!

#

!

"#

#'

#

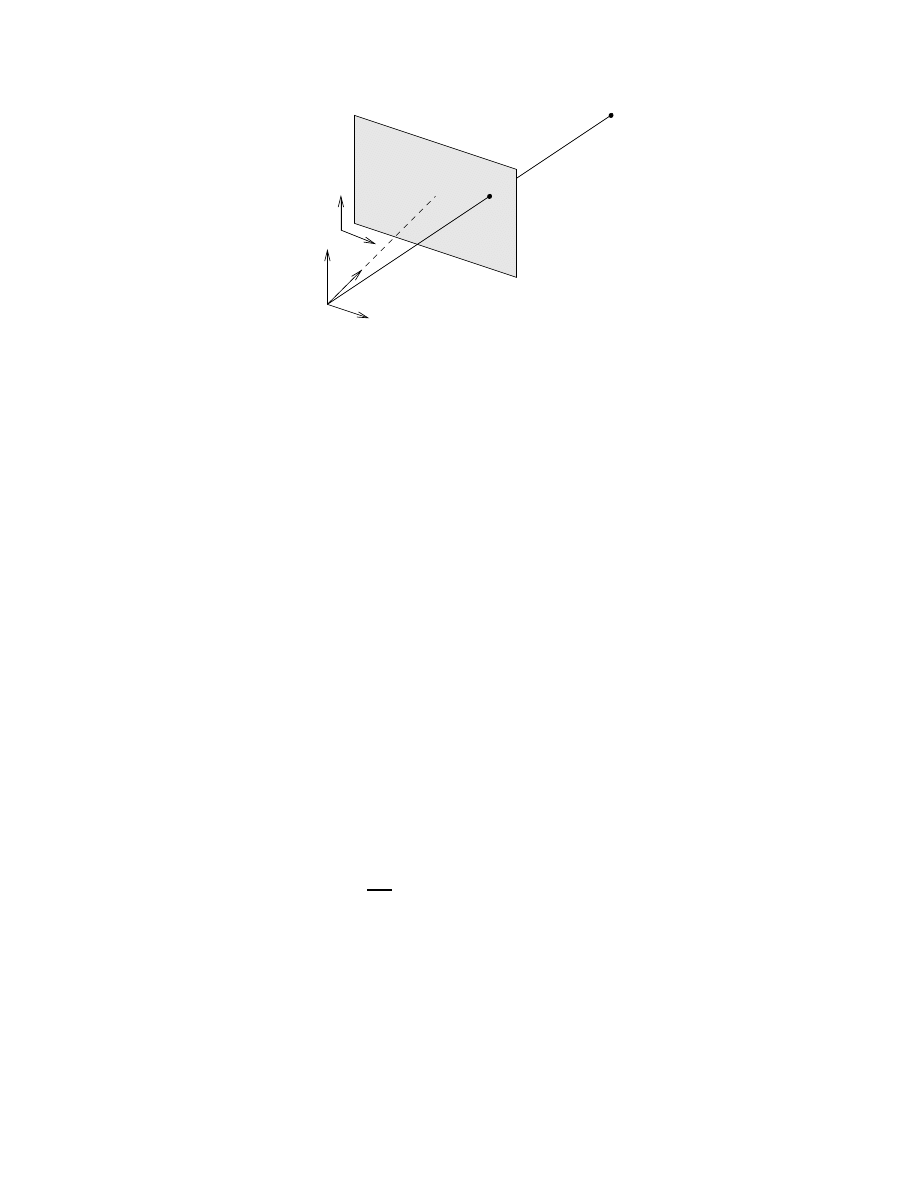
1

e

3

e

e

Optical

Centre

Camera 1

2

x

X

v

u

f

+

'

%

,

#!

,

#

%

#

,

#

Æ

!

#

!

-#

#

#

#

#

'

#

,

#

-#

!

E

#

#

#-#

#

#

!

#'

##

#

#

#

3

!

"

%

##

#%

7-

#

#

#

-#

#

!

I

#

!

#

#

#

#

!

#

(!8)!

#

!

/

*%

7

#

#

,

#

!

@

#

(

%

%

)

*

(

%

<

%

<

:

)

(!2)

$

#

%

%

,

(

#

)

#

#

#

#

#

9

:

(!2*)

,

%

#

%

!

H

,

-

-

,

!

#

##

7-#

#

%

#

!

9

½

 ½

!%

!%

(%

%

:

)

(!2&)

9

<

#

9

!

#

!

:

*

9

&

 

(!2)

%

#

&

!

5

(!2&)

9

(!2+)

#

9

(!2;)

"

#

9

(

)

9

(

)

(!22)

#

 

9

(

)

(!2)

H

 

9

(

)

(

)

:

(

)

*

9

(

)

(

)

9

(

)

(!28)

t -t

1

2

R

12

Line Distance

Camera 1

Camera 2

-

%

'

(

!

!

!

/

#

(!2)

#

-

(

)

%,

#

"

9

(

)

(

<

)

(

<

)

(

<

)

(

<

)

(!3)

#

!

/

(

)

#

#

!

(!3)

#

7

(

5%

!2)!

7

##

!

#

#%

(

)

#

!

#

#!

(!3)

#

!

/

#

#

9

3!

#

#

#

(

)

9

(!)

#

#

#

F

%

"

9

(

)

(

)

(!*)

9

(

<

)

(

<

)

(

<

)

(

<

)

(!&)

-

"

(!*)

#

9

#

9

(!)

@

#-

()

9

(!+)

#

#

!

9

()

9

(

)

9

"

(!;)

4

"

#

%

!

/

#

#

!

#

&%

!

K

#

#

#

#

-#

!

!

"#

6

#

#

&

!

/

,

%,

#

(!3)

#

!

"%

F

#

"

9

(

)

:

(

)

:

(

)

(

)

:

(

)

:

(

)

)

(!2)

9

(

<

)

(

<

)

(

<

)

(

<

)

!

(!)

@

# #

!

,

#

(

)

(

)

9

(*

)

(!8)

(

)

(

)

9

(*

)

(!83)

"

9

*

9

*

(!8)

;

;

:

*

*

:

9

&

(!8*)

()

9

!

(!8&)

/

*

"

!

#

-#

;

;

!

K

#

!

$

/

#

#!

M

#

#

#

!

$%

#

#

-#

#

,

#!

/

##

#

#

&%#!

1

#

#!

%

#

6

!

#

##

-#

!

I

,

#

!

'

##

%

#

-

!

4

#

#!

.

##

!

"

##

#

,

'

#

!

@

,

#

#

6

#

#

#!

%

L.

,

#

E4$

L!

N!

/

!4!

H

#

4!.!

6!

F

-

&%.

!

8;8O233

82!

* P!5!

L

!

!

/#

F#!

F#

8!

& L!

P!

F!

.!

!

.

L

#

0

88!

L!P!F!

.

/!K!

F

4!5!

#

P!

F

!

F

!

"

@!E!

6

#

!

"

;+O*&;!

6,

6

88;!

+ .!

H

#

!

4 1,!

!

$#

.#

8!

; 6!N!

!

H!

L#%

!

#

$

%

;*8O;*

82!

2

!4!

H

#

/!K!

K

!

I

#

#

/

!

&

*(*)*+*O*;

88!

P!

F

@!P!

51#

/!F!

F

#

L!P!F!

.!

K

#

/

#

!

#

'

*;(&)8

88!

8 P!

F

#

/!

4

!

0

%

!

"

E!

6

#

!

4 1,

#

(

&

)

&

!

6,

*333!

3 P!

#

Q!

!

E

#

%

#

/

,

!

#

'

*(&)**&O*&

88!

6!

4

#

P!N!

/

!

E

/

!

'

(

*

+(&)&38O

&*

88!

* .!4!

4!

+

&

,

!

#

0

88;!

& P!

@

!4!

H

#

K!

/

7!

I

#

/

#

%

!

(+)+O2;

88!

R!

R!

.

#

/

!

#

'

*2(*);O8+

88!