PROVA DE RACIOCÍNIO
1.
Qual a 2009
a
letra da seqüência: ABCDEDCBABCDEDCBABCDEDCBABCDEDCBABCDEDCB...?
a) A
d) D
b) B
e) E
c) C
2.
Efetuando o produto 99999...99
×
55555...55 obtemos um número cuja soma dos algarismos é igual a:
95 noves 95 cincos
a) 846
d) 954
b) 855
e) 1072
c) 945
3.
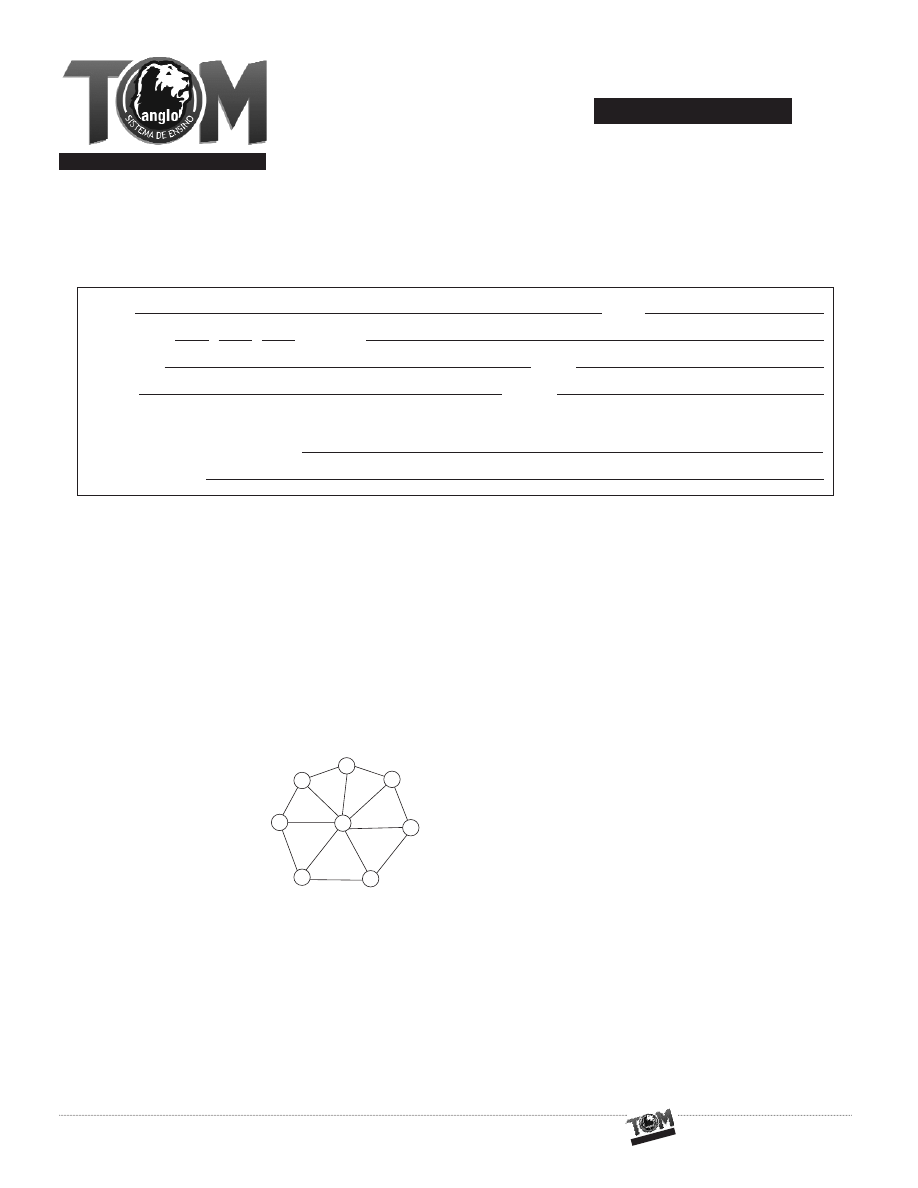
Na figura abaixo vamos colorir as bolinhas de acordo com a seguinte regra: se duas bolinhas estão ligadas por um
segmento de reta, então elas não podem ter a mesma cor.
O menor número de cores necessárias para isso é:
a) 3
d) 6
b) 4
e) 7
c) 5
4.
(Olimpíada Argentina) Considere a definição: Um inteiro b é um quadrado perfeito se, e somente se, existir um intei-
ro a tal que b = a
2
. Exemplos: 4 e 9 são quadrados perfeitos, pois 4 = 2
2
e 9 = 3
2
.
Com base nesta definição, o número de quadrados perfeitos compreendidos entre 7
4
e 4
7
é igual a:
a) 76
d) 82
b) 78
e) 84
c) 80
Nome:
Série:
Nascimento:
/
/
Endereço:
Tel.res/Cel:
e-mail:
Escola:
Cidade:
Já participou de alguma Olimpíada? Sim
□
Não
□
Em caso afirmativo, qual delas?
Já foi premiado?
SISTEMA ANGLO DE ENSINO
•
1
•
Treinamento para Olimpíadas de Matemática
2008
www.cursoanglo.com.br
2008
N
•
Í
•
V
•
E
•
L
3
Treinamento para
Olimpíadas de
Matemática
14243 14243
SISTEMA ANGLO DE ENSINO
•
2
•
Treinamento para Olimpíadas de Matemática
5.
(Olimpíada da Cone Sul 2007–adaptada) Considere um tabuleiro 2007
×
2007. São pintadas algumas casas do
tabuleiro. Dizemos que o tabuleiro é charrua se nenhuma linha está totalmente pintada e nenhuma coluna está to-
talmente pintada. Qual é o número máximo de casas pintadas que um tabuleiro charrua pode ter?
a) 2008
d) 2006
×
2007
b) 2007
2
e) 2006
×
2008
c) 2006
2
6.
(OBM) Dois pontos A e B de um plano
α
estão a 8 unidades de distância. Quantas retas do plano
α
estão a 2 uni-
dades de A e 3 unidades de B?
a) 1
d) 4
b) 2
e) 5
c) 3
7.
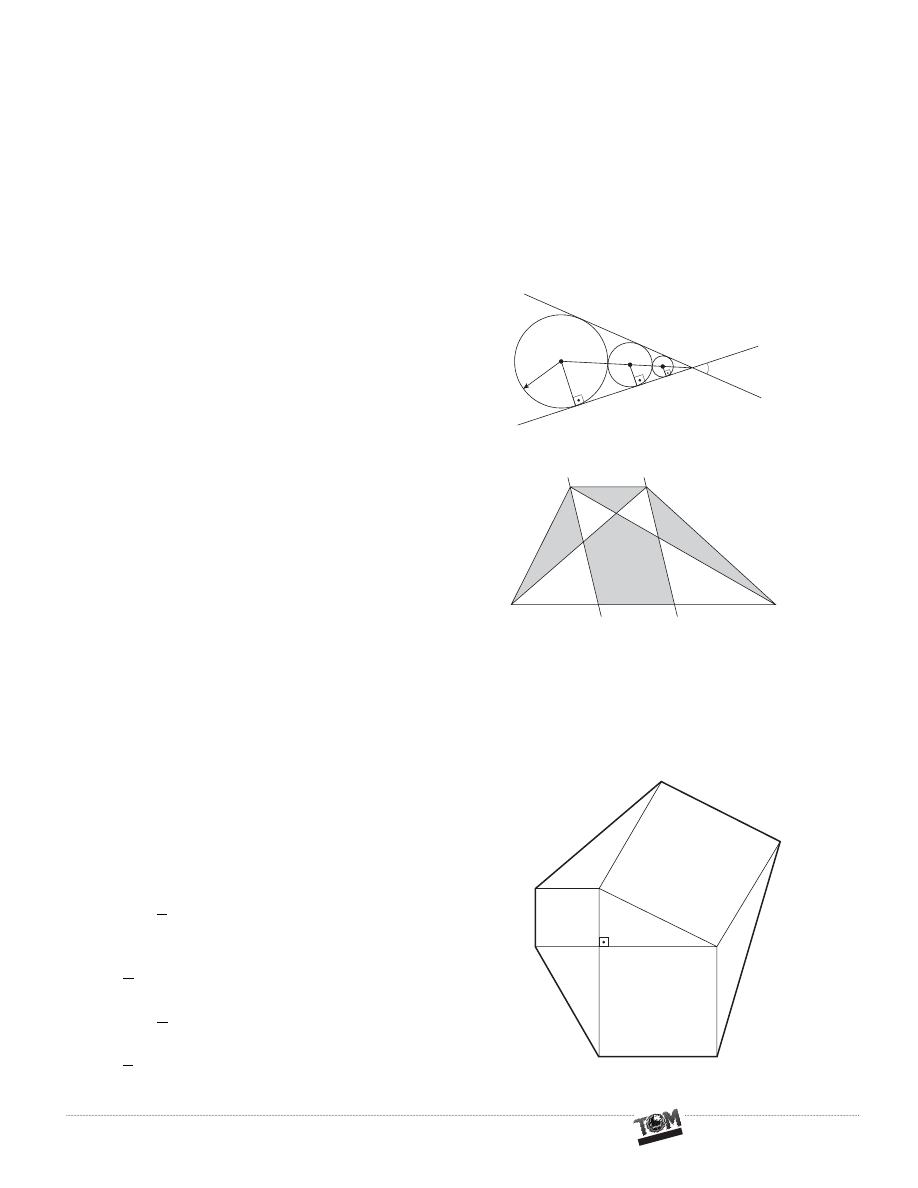
(Olimpíada Americana) Considerando a figura ao lado,
qual o valor mais próximo para a soma dos diâmetros
dos três círculos:
a) 7
b) 6
c) 8
d) 12
e) 15
8.
(Olimpíada Argentina) No trapézio ABCD estão traçadas
as diagonais e duas retas paralelas entre si, uma por A e
a outra por B. (Ver figura ao lado)
Indicamos por
b, c, e d as áreas dos triângulos sombrea-
dos e por
a área do pentágono sombreado, nestas con-
dições podemos afirmar que:
a) a = b + d – 2c
b) a = b + d – 3c
c) a = 2b + 2d + c
d) a = b + d + 2c
e) a = b + d + c
9.
(Olimpíada Argentina) No paralelogramo ABCD os lados AB e CD medem 5 e os lados AD e BC medem 6. Traça-
se a bissetriz do ângulo  que corta o lado BC no ponto E, então 2 BE + 3 EC =
a) 11
d) 14
b) 12
e) 15
c) 13
10. (Olimpíada Italiana) Um hexágono convexo é obtido a partir
de quadrados construídos sobre os lados de um triângulo re-
tângulo de catetos medindo p e q, conforme mostra-se na
figura ao lado.
Nestas condições, a área do hexágono em função de p e q,
é igual a
a) pq +
(p
2
+ q
2
)
b) 2pq + 2(p
2
+ q
2
)
c)
pq + 2(p
2
+ q
2
)
d) pq +
(p
2
+ q
2
)
e)
pq + 2(p
2
+ q
2
)
5
2
3
2
3
2
5
2
2008
4
O
P
Q
C
B
A
D
60
°
F
E
C
D
b
a
d
c
A
B
p
q