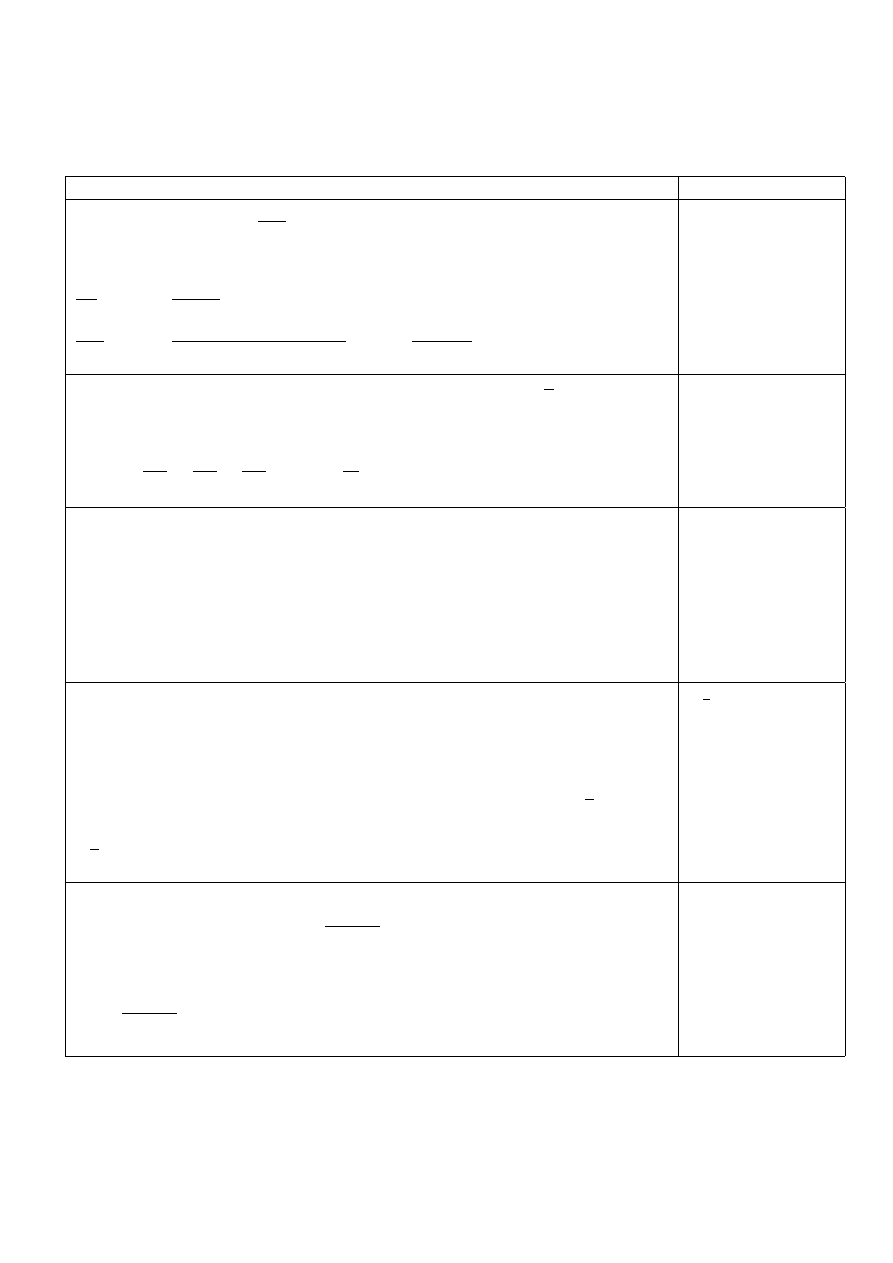
Egzamin z Analizy 2, 16 VI 2011 godz. 12.00
1. Zadanie wstępne
Zadanie
Odp.
1. Obliczyć pochodną
∂
2
f
∂x
2
(P ) , gdzie f (x, y) = x
3
+ y
3
+ y ln(x
2
− 3)
,
P = (2, 2)
Rozwiązanie:
∂f
∂x
= 3x
2
+
y · 2x
x
2
− 3
∂
2
f
∂x
2
= 6x +
2y · (x
2
− 3) − 2xy · 2x
(x
2
− 3)
2
= 12 +
4 − 32
(4 − 3)
2
= −16
−16
2. Obliczyć dywergencję pola wektorowego
−
→
F =
h
2x
2
y + z ,
x
y
, x
2
z + yz
2
i
w
punkcie P = (1, −1, 0)
Rozwiązanie:
div ~
F =
∂P
∂x
+
∂Q
∂y
+
∂R
∂z
= 4xy −
x
y
2
+ x
2
+ 2yz = −4 − 1 + 1 + 0 = −4
−4
1.3 Obliczyć całkę iterowaną
1
Z
0
1−x
Z
0
(2x + 4y) dy
dx
Rozwiązanie:
1
Z
0
1−x
Z
0
(2x + 4y) dy
dx =
1
Z
0
h
2xy + 2y
2
i
1−x
0
dx =
1
Z
0
(2 − 2x) dx =
h
2x − x
2
i
1
0
=
1
1
1.4 Obliczyć całkę krzywoliniową skierowaną
Z
C
y dx + 2x dy ;
C :
x = t
2
, y = 1 − t
2
od t = 0 do t = 1
Rozwiązanie:
Z
C
y dx+x dy =
1
Z
0
(1−t
2
)·2t dt+2t
2
·(−2t) dt =
1
Z
0
(−6t
3
+2t) dt =
h
−
6
4
t
4
+t
2
i
1
0
=
−
1
2
−
1
2
1.5 Zapisać zbiór A we współrzędnych walcowych w postaci normalnej:
A :
x
2
+ y
2
¬ 9 , z ¬ 4 , z
√
x
2
+ y
2
Rozwiązanie:
x
2
+ y
2
¬ 9 =⇒ r
2
¬ 9 =⇒ r ¬ 3
pierwszy warunek (walec)
z ¬ 4
drugi warunek (płaszczyzna)
z
√
x
2
+ y
2
=⇒ z r
trzeci warunek (stożek)
0 ¬ ϕ ¬ 2π
0 ¬ r ¬ 3
r ¬ z ¬ 4
1
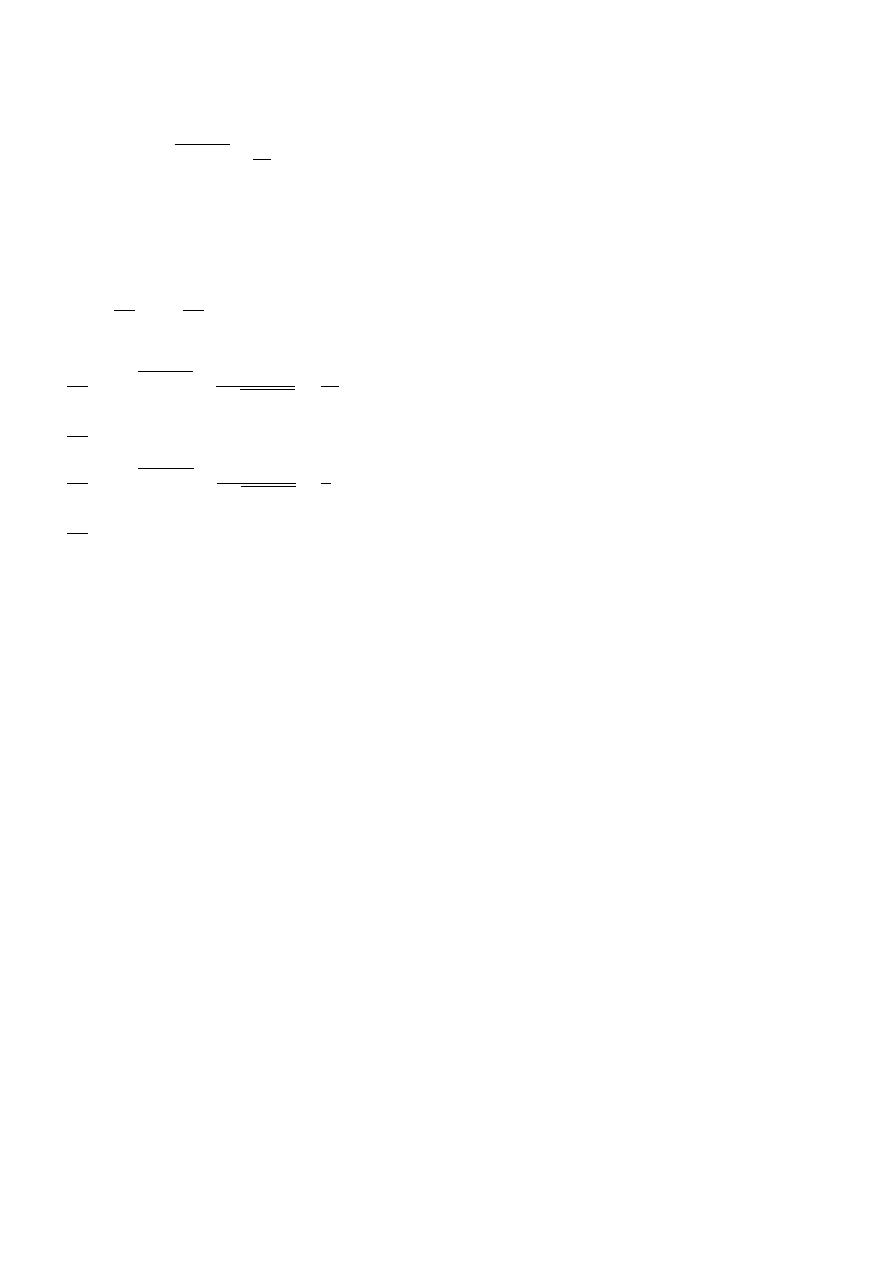
2. Wyznaczyć różniczkę zupełną funkcji
f (x, y) = xy
q
x
3
− y
2
+
4y
x
+ sin(y
2
− 2x)
w punkcie P (2, 2) . Wyznaczyć płaszczyznę styczną do powierzchni z = f (x, y) w
punkcie leżącym nad P
Rozwiązanie:
Różniczka zupełna funkcji f jest równa:
df =
∂f
∂x
dx +
∂f
∂y
dy
Obliczamy:
∂f
∂x
= y
q
x
3
− y
2
+
xy · 3x
2
2
√
x
3
− y
2
−
4y
x
2
+ cos(y
2
− 2x) · (−2)
∂f
∂x
(P ) = 4 + 12 − 2 − 2 = 12
∂f
∂y
= x
q
x
3
− y
2
+
xy · (−2y)
2
√
x
3
− y
2
+
4
x
+ cos(y
2
− 2x) · (2y)
∂f
∂y
(P ) = 4 − 4 + 2 + 4 = 4 = 6
Różniczka zupełna f w punkcie P jest równa
df = 12 dx + 6 dy
Równanie płaszczyzny stycznej π do powierzchni z = f (x, y) :
z − z
0
= 12(x − x
0
) + 6(y − y
0
)
z
0
= f (x
0
, y
0
) = 2 + 4 + 0 = 6
z − 6 = 12(x − 2) + 6(y − 2)
π :
12x + 6y − z − 18 = 0
2
3. Znaleźć ekstrema lokalne funkcji
f (x, y) = 2x
2
y + xy
2
− 6xy
Rozwiązanie:
Dziedzina funkcji D : R
2
-zbiór otwarty, f jest klasy C
2
Rozwiązujemy układ równań :
∂f
∂x
= 0
;
∂f
∂y
= 0
Obliczamy pochodne cząstkowe:
∂f
∂x
= 4xy + y
2
− 6y
;
∂f
∂y
= 2x
2
+ 2xy − 6x
Stąd:
(
4xy + y
2
− 6y = 0
2x
2
+ 2xy − 6x = 0
y(4x + y − 6) = 0
pierwsze równanie
Czyli y = 0 lub 4x + y − 6 = 0
Dla y = 0 z drugiego równania:
2x
2
− 6x = 0 =⇒ 2x(x − 3) = 0 =⇒ x = 0 lub x = 3
Dla 4x + y − 6 = 0 = 0 =⇒ y = 6 − 4x z drugiego równania:
2x
2
+ 12x − 8x
2
− 6x = 0 =⇒ 6x(−x + 1) = 0 =⇒ x = 0 lub x = 1
x = 0 =⇒ y = 6
x = 1 =⇒ y = 2
Mamy więc cztery punkty stacjonarne:
P
1
(0, 0) , P
2
(3, 0) , P
3
(0, 6) , P
4
(1, 2)
Obliczamy pochodne cząstkowe drugiego rzędu:
∂
2
f
∂x
2
= 4y
;
∂
2
f
∂y
2
= 2x
;
∂
2
f
∂x∂y
= 4x + 2y − 6
Badamy macierz drugich pochodnych :
f
00
(P
1
) =
"
0 −6
−6
0
#
W
1
= 0 , W
2
= −36 < 0
w P
1
nie ma ekstremum
f
00
(P
2
) =
"
0 6
6 6
#
W
1
= 0 , W
2
= −36 < 0
w P
2
nie ma ekstremum
f
00
(P
3
) =
"
24 6
6 0
#
W
1
= 24 > 0 , W
2
= −36 < 0
w P
3
nie ma ekstremum
f
00
(P
4
) =
"
8 2
2 2
#
W
1
= 8 > 0 , W
2
= 12 > 0
w P
4
jest minimum lokalne
3
4. Obliczyć moment bezwładności względem osi Oy jednorodnego obszaru: xy ¬ 8 ,
y x
2
, x 0 , y ¬ 8
Rozwiązanie:
I
y
=
ZZ
D
ρx
2
dx dy = ρ
Z Z
D
x
2
dx dy
gdzie ρ jest gęstością obszaru.
Zbiór D dzielimy na dwie części:
D
1
:
(
0 ¬ x ¬ 1
x
2
¬ y ¬ 8
D
2
:
(
1 ¬ x ¬ 2
x
2
¬ y ¬
8
x
Mamy:
ZZ
D
x
2
dx dy =
ZZ
D
1
x
2
dx dy +
ZZ
D
2
x
2
dx dy
Obliczamy:
ZZ
D
1
x
2
dx dy =
1
Z
0
8
Z
x
2
x
2
dy
dx
8
R
x
2
x
2
dy =
h
x
2
y
i
8
x
2
= 8x
2
− x
4
1
R
0
(8x
2
− x
4
) dx =
h
8
3
x
3
−
1
5
x
5
i
1
0
=
8
3
−
1
5
=
37
15
ZZ
D
2
x
2
dx dy =
2
Z
1
8
x
Z
x
2
x
2
dy
dx
8
x
R
x
2
x
2
dy =
h
x
2
y
i
8
x
x
2
= 8x − x
4
2
R
1
(8x − x
4
) dx =
h
4x
2
−
1
5
x
5
i
2
1
= 16 −
32
5
− (4 −
1
5
) =
29
5
I
y
= ρ(
37
15
+
29
5
) =
124ρ
15
Odpowiedź:
I
y
=
124ρ
15
4
5. Obliczyć
ZZ Z
A
y
2
z
2
dx dy dz , jeżeli bryła A jest ograniczona powierzchniami x
2
+y
2
= 4
, x
2
+ y
2
= z
2
.
Rozwiązanie:
z
2
= x
2
+ y
2
: stożek
x
2
+ y
2
= 4 : walec
Stosujemy współrzędne walcowe:
I =
ZZ Z
A
∗
zr
2
sin
2
ϕ · r dr dϕ dz =
Z Z Z
A
∗
zr
3
sin
2
ϕ dr dϕ dz
Zbiór A
∗
:
x
2
+ y
2
= 4 =⇒ r
2
= 4 =⇒ r = 2
z
2
= x
2
+ y
2
=⇒ z
2
= r
2
=⇒ z = ±r
zachodzić mają również standardowe ograniczenia współrzędnych walcowych: r 0
oraz ϕ należy do jednego okresu. Stąd:
A
∗
: ϕ ∈< 0, 2π > ; r ∈< 0, 2 > ; z ∈< −r, r >
I =
2π
Z
0
sin
2
ϕ dϕ
·
2
Z
0
r
Z
−r
z
2
r
3
dz
dr
2π
Z
0
sin
2
ϕ dϕ =
2π
Z
0
1 − cos 2ϕ
2
dϕ =
1
2
h
ϕ −
1
2
sin 2ϕ
i
2π
0
= π
r
Z
−r
z
2
r
3
dz =
h
1
3
z
3
r
3
i
r
−r
=
1
3
r
6
+
1
3
r
6
=
2
3
r
6
2
Z
0
1
3
r
6
dr =
h
2
21
r
7
i
2
0
=
256
21
Odpowiedź:
I =
256π
21
5
6. Sprawdzić twierdzenie Greena jeżeli zbiór A : y x
2
, y ¬ 2 − x ; a pole wektorowe
[P, Q] = [x
2
, xy]
Rozwiązanie:
Szukamy punktów przecięcia krzywych:
(
y = x
2
y = 2 − x
=⇒ x
2
= 2 − x =⇒ x
2
+ x − 2 = 0 =⇒ x = −2 lub x = 1
Wzór Greena:
ZZ
A
∂Q
∂x
−
∂P
∂y
!
dx dy =
I
K
P dx + Q dy
Obliczamy lewą stronę. A jest obszarem normalnym:
A :
(
−2 ¬ x ¬ 1
x
2
¬ y ¬ 2 − x
Obliczamy:
∂Q
∂x
−
∂P
∂y
= y − 0 = y
L =
ZZ
A
y dx dy =
1
Z
−2
2−x
Z
x
2
y dy
dx
2−x
Z
x
2
y dy =
h
1
2
y
2
i
2−x
x
2
=
1
2
(2 − x)
2
−
1
2
x
4
= 2 − 2x +
1
2
x
2
−
1
2
x
4
L =
1
R
−2
2 − 2x +
1
2
x
2
−
1
2
x
4
dx =
h
2x − x
2
+
1
6
x
3
−
1
10
x
5
i
1
−2
= 2 − 1 +
1
6
−
1
10
− (−4 −
4 −
8
6
+
32
10
) = 9 +
9
6
−
33
10
=
72
10
=
36
5
Krzywa K jest brzegiem zbioru A zorientowanym dodanio (w lewo). Dzielimy K na 2
łuki:
Obliczamy całki:
K
1
: x = t , y = t
2
; t zmienia się od −2 do 1
Z
K
1
x
2
dx + xy dy =
1
Z
−2
(t
2
· 1 + t
3
· 2t) dt =
1
Z
−2
(t
2
+ 2t
4
) dt
1
3
t
3
+
2
5
t
5
1
−2
=
1
3
+
2
5
− (−
8
3
−
64
5
) = 3 +
66
5
K
2
: x = t , y = 2 − t ; t zmienia się od 1 do −2
Z
K
2
x
2
dx + xy dy =
−2
Z
1
(t
2
· 1 + t(2 − t) · (−1)) dt =
−2
Z
1
(2t
2
− 2t) dt =
2
3
t
3
− t
2
−2
1
=
−16
3
− 4 − (
2
3
− 1) = −9
Stąd:
P = 3 +
66
5
− 9 =
36
5
Czyli lewa strona jest równa prawej stronie.
6