The drying kinetics of kale (Brassica oleracea)

in a convective hot air dryer

Gikuru Mwithiga

*

, Joseph Ochieng Olwal

Biomechanical and Environmental Engineering Department, Jomo Kenyatta University of Agriculture and Technology, P.O. Box 62000, Nairobi, Kenya

Received 16 August 2004; accepted 24 October 2004

Available online 10 December 2004

Abstract

The effect of air temperature and sample thickness on the drying kinetics of kale was investigated using a convective air dryer at a

fixed airflow rate of 1 m/s and drying air temperatures of 30, 40, 50 and 60

C. The sliced kale leaves were dried in wire trays in 10,

20, 40 and 50 mm thick layers. The drying rate increased with drying air temperature but decreased with layer thickness. The effec-
tive diffusivity for 10 mm thick layers was found to increase with the drying air temperature and ranged between 14.9 and
55.9

· 10

10

m

2

/s. The effect of temperature on diffusivity could be expressed by an Arrhenius type relationship with a high R

2

of 0.9989. The activation energy of kale was found to be 36.115 kJ/mol. When four drying models were developed using the exper-
imental data the Modified Page model was found to be marginally better than the other models in estimating the drying curve over
the experimental temperature range.
2004 Elsevier Ltd. All rights reserved.

Keywords: Kale; Drying time; Modeling; Diffusivity; Activation energy

1. Introduction

The green vegetable kale (Brassica Oleracea) is com-

monly referred to in Kenya as the poor manÕs vegetable
of choice. It is widely grown in all the East African
countries and in many other parts of the world including
Europe, Asia and Latin America. This leafy vegetable
has high amounts of vitamins as well as other micronu-
trients and is well ranked in terms of nutrition among
members of the cabbage family. However, it has a high
moisture content (approximately 86% wb.) at harvest
and therefore cannot be preserved for more than a few
days under ambient conditions of 20–25

C (

Imungi,

1992

). Although refrigeration would be an ideal way

of preserving kale in its fresh form, in Kenya less than
4% of the population have access to refrigerators and

it is therefore necessary to find other methods of pre-
serving fresh produce (

Karekezi & Ranja, 1997

).

Drying of vegetables as a means of improving stor-

ability has been practiced for may centuries. Compared
to fresh vegetables which can only keep for a few days
under ambient conditions, dry products can be stored
for months or even years without appreciable loss of
nutrients. Drying vegetables also reduces the bulk
weight thus facilitating ease of transportation. In some
cases drying may lead to a considerable reduction in vol-
ume and hence reduction in storage space requirements.
Also, vegetable yields usually shoot up following the
rain season thus forcing prices to dramatically fall. Dry-
ing kale at this time of plenty will help to reduce price
fluctuations while increasing incomes for the producers.
Fresh produce losses that can at times be as high as 70%
can also be avoided (

Waithaka, 1992

).

Thin layer drying studies normally form the basis of

understanding the drying characteristics of food mate-
rials since every material is unique. The results of such

0260-8774/$ - see front matter

2004 Elsevier Ltd. All rights reserved.

doi:10.1016/j.jfoodeng.2004.10.041

*

Corresponding author. Fax: [phone].

E-mail address:

[e-mail]

(G. Mwithiga).

www.elsevier.com/locate/jfoodeng

Journal of Food Engineering 71 (2005) 373–378

studies are used to simulate dryers under deep-bed dry-
ing conditions and can also form the basis for design of
specialized drying equipment. There have been many
studies on thin layer drying of grains (

Cao, Nishiyama,

Koide, & Lu, 2004

;

Gaston, Abalone, Giner, & Bruce,

2004

), fruits (

Doymaz, 2004a, 2004c

;

Simal, Femenia,

Garau, & Rossello, 2005

;

Velic´, Planinic´, Thomas, &

Bilic´, 2004

), vegetables (

Doymaz, 2004b

), leaves and

grasses (

Demir, Gunhan, Yagcioglu, & Degirmencioglu,

2004

;

OÕcallaghan, Menzzies, & Bailey, 1974

). However

the authors have not found any literature on the thin
layer drying of kale leaves.

Thin layer drying models used in the analysis of dry-

ing characteristics are usually theoretical, semi-theoreti-
cal or purely empirical. Some semi-theoretical drying
models which have been widely used are presented
in form of Eqs.

(1)–(4)

(

Lahsansi, Kouhila, Mahrouz,

& Jaouhari, 2004a

;

Lahsansi, Kouhila, Mahrouz,

Mohamed, & Agorram, 2004b

;

Senadeera, Bhandari,

Young, & Wijesinghe, 2003

;

Sharma & Prasad, 2004

;

Simal et al., 2005

;

Sogi, Shivhare, Garg, & Bawa,

2003

;

Togrul & Pehlivan, 2004

).

Newton model

MR

¼ expðktÞ

ð1Þ

Page model

MR

¼ expðkt

n

Þ

ð2Þ

Modified Page model

MR

¼ exp½ðk tÞ

n

ð3Þ

Henderson and Pabis model

MR

¼ a expðktÞ

ð4Þ

These models are closely related to the diffusivity

equation based on Ficks theory that is present in Eq.

(5)

. On integration and simplification, this equation

can be reduced to the form of Eq.

(6)

for slab like mate-

rials with good accuracy (

MaCabe, Smith, & Harriott,

1993

).

dM =dt

¼ ðp=2Þ

2

D

v

=L

2

M

ð5Þ

MR

¼ ½8=p

2

exp½ðp

2

D

v

=L

2

Þt

ð6Þ

Eq.

(6)

can further be modified to Eq.

(7)

representing a

linear relationship between the logarithm of moisture
ratio and time. From a plot of ln(MR) versus time the

slope is represented by constant B in Eq.

(7)

and hence

the moisture diffusivity can be determined.

ln MR

¼ A þ Bt

ð7Þ

where A = 8/p

2

and B = [(p

2

D

v

/L

2

)].

Values of moisture diffusivity for foods have been

listed by

Doulia, Tizia, and Gekas (2000)

and fall be-

tween a low of 0.8

· 10

13

m

2

/s for raisin wheat at

20

C and a high of 64.6 · 10

10

m

2

/s for tomato con-

centrates (15% solids) at 100

C. The D

v

values have also

been found to increase with temperature of drying air
and in many cases the variation of the diffusivity assume
an Arrhenius-type relationship represented by Eq.

(8)

.

The activation energy of the material can be calculated
from this equation.

ln

ðD

v

Þ ¼ C DH =ðRT

abs

Þ

ð8Þ

In view of the fact that no literature was available on

the drying characteristics of kale, the present study aims
to determine these characteristics in the temperature
rage of 30–60

C and to study the effect of layer thick-

ness and drying air temperature on drying time.

2. Materials and methods

2.1. Equipment

The dryer used in these experiments is presented in

Fig. 1

and consisted of a centrifugal fan that was used

to blow air into the heating unit through a 100 mm
diameter metallic duct. By using a metal flap to control
the fan opening, the amount of air delivered could be in-
creased from no airflow at all (when fully closed) to a
maximum of 22 m

3

/min when the fan was fully open.

However, in all experiments the flap opening was set
to deliver air to the drying sample at a velocity1m/s
and could maintain flowrate within ±0.05 m/s.

The heating unit was made of an inner chamber

(25

· 25 · 25 cm) made of a mild steel sheet that was

in turn enclosed in an outer chamber (35

· 35 · 35 cm)

made of soft board. The space between the two cham-

Nomenclature

A, B

regression constants

D

v

moisture diffusivity, m

2

/s

k

drying rate constant, min

1

L

slab thickness, m

MR

moisture ratio = (M

0

M)/(M

0

M

e

)

M

moisture content at any time t, decimal dry
basis, kg

w

/kg

db

M

0

initial moisture content, decimal dry basis,
kg

w

/kg

db

M

e

equilibrium moisture content, decimal dry
basis, kg

w

/kg

db

R

universal gas constant, 8.314 J/mol K

T

temperature,

C

T

abs

absolute temperature, K

t

time, min

DH

activation energy, J/mol

374

G. Mwithiga, J.O. Olwal / Journal of Food Engineering 71 (2005) 373–378

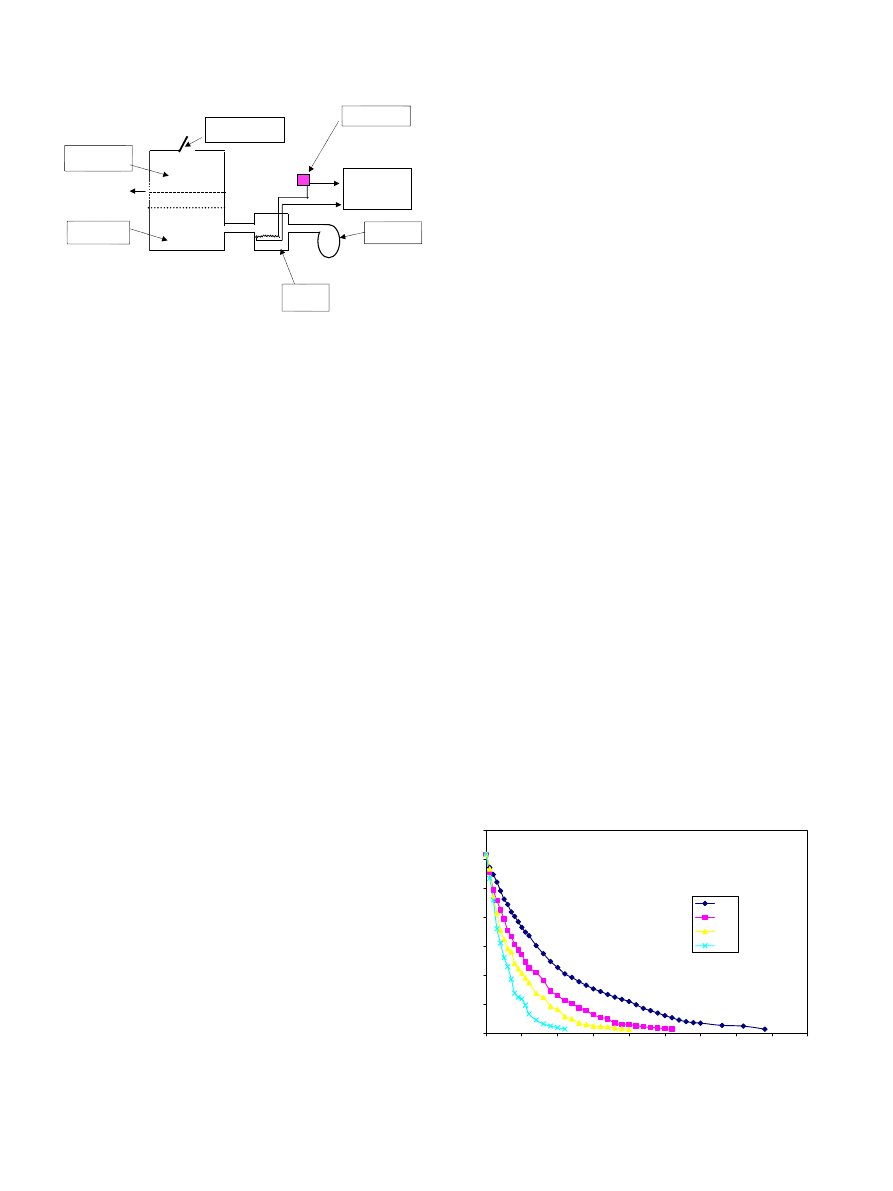
bers was filled with fiberglass insulating materials. On
leaving the heating chamber the air passed through a
37

· 37 · 25 cm plenum chamber to allow it to mix

and achieve uniform temperature before entering the
drying chamber.

Inserted into the heating chamber were three 1.5 kW

electric coils. The coils were connected to the electric
mains through an on/off digital temperature controller
(model ESEX-A, Omron corporation, Japan). The con-
troller was set to switch on the heating coils whenever
the temperature in the drying chamber fell to more than
one degree below the set temperature and to switch off
the coils as soon as the drying chamber temperature ex-
ceeded the set temperature by more than one degree cen-
tigrade. Thus the temperature controller could maintain
the set temperature to within ±2

C using the signal

from a T-type thermocouple inserted into the drying
chamber.

2.2. Experiments

Fresh kale leaves were harvested from the Jomo

Kenyatta University of Agriculture and Technology
farm and immediately used for the drying experiments.
The leaves were prepared for drying by chopping them
into thin slices of approximately 3 mm width. The sliced
material was then divided into three portions with one
portion being used for initial moisture content determi-
nation while the other two were put into wire-mesh trays
and used as replicates in the convective hot air dryer.

During the drying experiments the temperature of the

dryer was first raised to the set temperature and the
steady conditions maintained for at least 30 min before
inserting the samples. The sample was then loosely
spread on a wire-mesh tray to the required depth raging
from 10 to 50 mm. The mass of sample was measured
using a digital balance, measuring to an accuracy of
0.001 g, immediately before inserting it into the dryer.
Thereafter the mass was periodically taken by briefly
removing the sample from the dryer. The velocity of
the air during drying was set at 1 m/s and the sample

was dried until the moisture content was 16% (db) or
lower. The initial moisture content was determined fol-
lowing the ASAE recommended method for forage
materials (

ASAE Standards, 1997

).

Thin layer drying experiments were done using

10 mm thick samples layer and at temperatures of 30,
40, 50 and 60

C. This sample thickness was considered

shallow enough to allow the sliced kale leaves in the
layer to be fully exposed to the drying air and these
experiments were therefore later used in the determina-
tion of thin layer drying characteristics of kale.

Additional experiments to determine the effect of

loading depth on the rate of drying were done at loading
depths of 20, 40 and 50 mm and drying temperatures of
30, 40, 50 and 60

C.

3. Results and discussion

Fig. 2

shows the variation of moisture content with

time when drying 10 mm thick kale layers within the
temperature range of 30–60

C. The initial moisture con-

tent of kale was observed to be 6.172 db. (86.06% wb.)
which is characteristic of most high moisture vegetables.
From

Fig. 2

it is clearly evident that the drying time de-

creased dramatically with increase in drying air temper-
ature. The drying time required to lower the moisture
contents to 2.0 (decimal dry basis) or lower when using
an air temperature of 30

C was approximately twice

that required at a drying air temperature of 50

C. When

the thickness of the kale layer was increased (

Figs. 3–5

)

the same trend in the relationship between drying time
and temperature was observed in that drying time at a
drying air temperatures of 30

C was always approxi-

mately twice that at 50

C.

The drying time also increased with the depth of

material. The drying time required to lower the mois-

0

1

2

3

4

5

6

7

0

50

100

150

200

250

300

350

400

450

Time, minutes

Moisture content, decimal dry basis

30˚C

40˚C

50˚C

60˚C

Fig. 2. Variation of moisture content with time and drying air
temperature when drying kale in 10 mm thick layers.

1kW centrifugal
fan

Swing door opening for
sampling

Drying chamber

Plenum chamber

Temperature
controller

To electric
power source

Airflow

Air heating
chamber

Fig. 1. A schematic view of dryer used in the drying experiments.

G. Mwithiga, J.O. Olwal / Journal of Food Engineering 71 (2005) 373–378

375

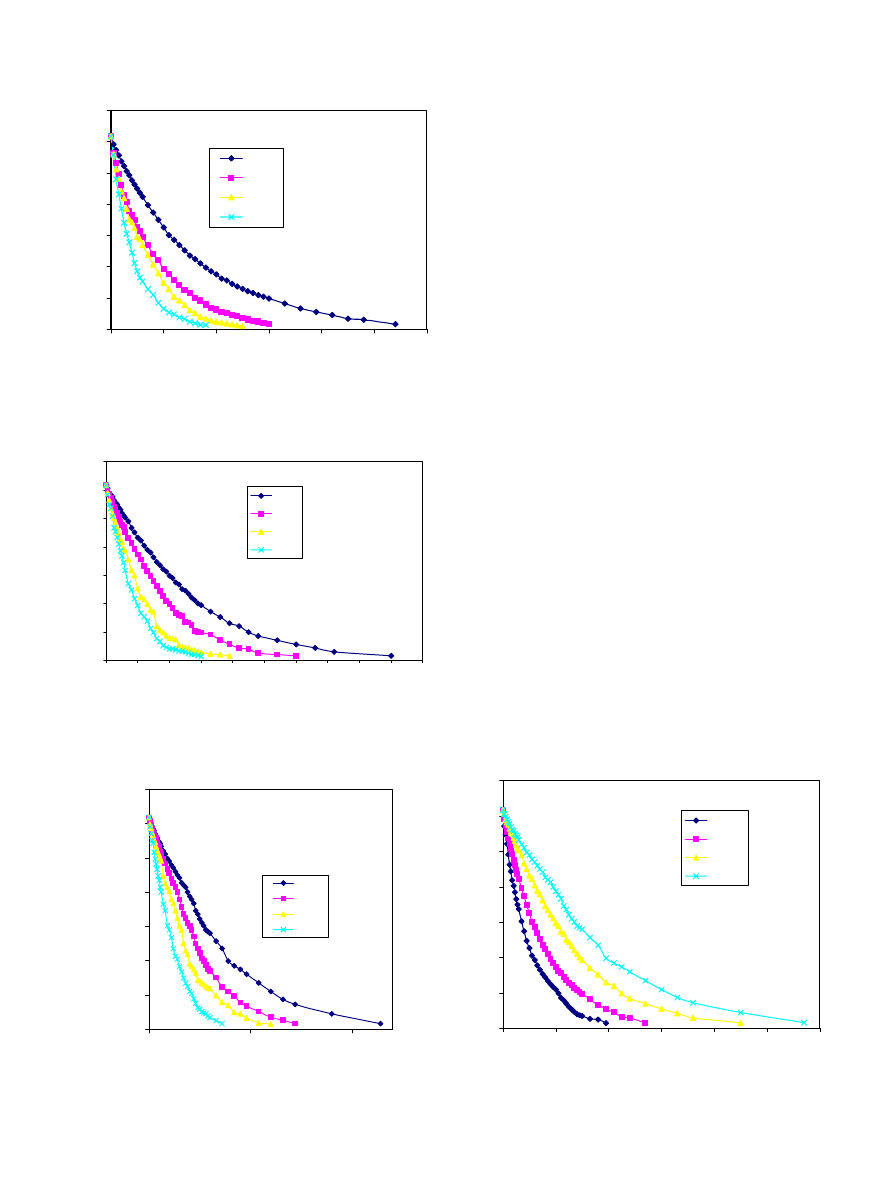
ture content of kale from 6.172 db. (86.06% wb.) to
approximately 0.15 db. (13.04% wb.) increased from
390 min (6.5 h) for a 10 mm layer and drying air temper-
ature of 30

C to about 1200 min (20 h) when the layer

depth was increased to 50 mm as can be seen in

Fig. 6

.

Similarly, the drying time increased with depth of drying
kale at drying air temperatures of 40, 50 and 60

C.

After computing the moisture ratio using the thin

layer (10 mm thick) drying data, the STATGRAPHICS
(Version 7.0 for DOS, Manguistics Inc, Cambridge,
MA) statistical software package for non-linear regres-
sion analysis was used to fit moisture ratio against dry-
ing time and determine constants of Eqs.

(1)–(4)

for the

four selected drying models. The regression constants,
and coefficient of determination (R

2

) for these four

models are given in

Table 1

. From the table, it is obvi-

ous that the Page models have higher R

2

and therefore

represents the drying characteristics of kale (for individ-
ual drying runs) better than either the Newton or the
Henderson and Pabis model. Also, the drying rate con-
stants presented in

Table 1

fall within the range of those

complied by

Krokida, Foundoukidis, and Maroulis

(2004)

.

To take into account the effect of temperature on dry-

ing rate, the rate constants of each model were corre-
lated against temperature. However, the average values
of constants a and n over the experimental temperature
range were used. Consequently the equations in

Table 2

,

representing the drying characteristics of kale under
convective drying within the range 30–60

C, for each

of the drying models were developed.

These equations (

Table 2

) were used to estimate the

moisture ratio of kale using the drying time data and
the estimated values consequently compared to experi-
mental values. The R

2

and the standard error of estimate

0

1

2

3

4

5

6

7

0

200

400

600

800

1000

1200

Time, minutes

Moisture

c

onte

nt, de

ci

ma

l dry ba

sis

10 mm

20 mm

40 mm

50 mm

Fig. 6. Variation of moisture content with drying time and layer
thickness when drying kale at a drying air temperature of 30

C.

0

1

2

3

4

5

6

7

0

500

1000

Time, minutes

Moistur

e c

ontent, de

cimal dr

y ba

sis

30

˚

C

40

˚

C

50

˚

C

60

˚

C

Fig. 5. Variation of moisture content with drying time and air
temperature when drying kale in 50 mm thick layers.

0

1

2

3

4

5

6

7

0

100

200

300

400

500

600

Time, minutes

Moisture ratio, de

cimal dr

y ba

sis

30

˚C

40

˚

C

50

˚

C

60

˚

C

Fig. 3. Moisture content of kale as a function of drying time and air
temperature when drying kale at a layer depth of 20 mm.

0

1

2

3

4

5

6

7

0

100

200

300

400

500

600

700

800

900

1000

Time, minutes

Moistur

e c

onte

n

t, decimal dry basis

30˚C

40˚C

50˚C

60˚C

Fig. 4. Variation of moisture content with drying time and air
temperature when drying kale in 40 mm thick layers.

376

G. Mwithiga, J.O. Olwal / Journal of Food Engineering 71 (2005) 373–378

(SEE), for the goodness of fit for each of the models,
over the air temperature range of 30–60

C are also

given in

Table 2

. It can be seen that all models have high

values of R

2

and low values of SEE when compared to

the R

2

values of 0.764–0.981 found by

Akpinar, Bicer,

and Midili (2003)

while in the case of drying apple slices

in a convective dryer within the temperature range of
60–80

C. However, the coefficients of the Modified

Page model are marginally superior showing that the
model best represents the drying behaviour of kale.

Fig. 7

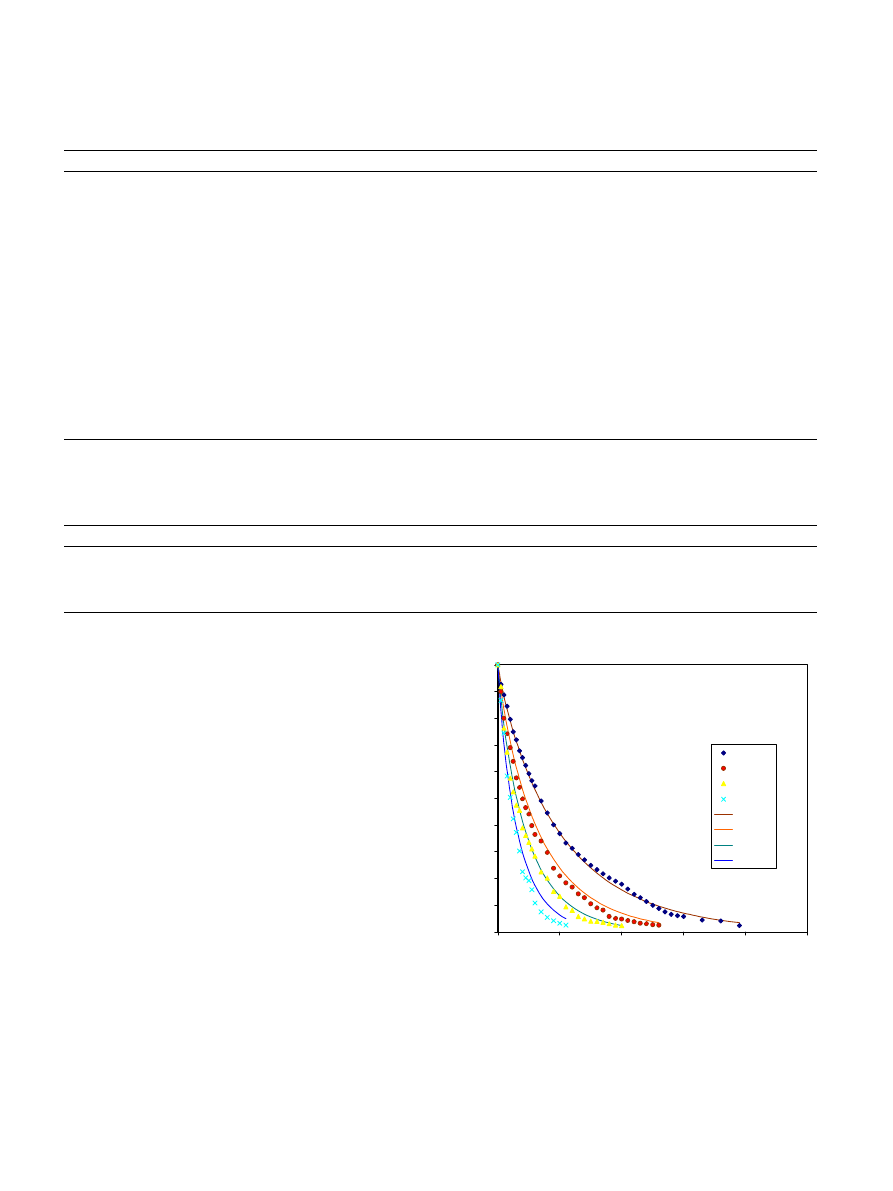
shows experimental moisture ratio values as a

function of time when plotted alongside those predicted
using the Modified Page model. Clearly, the Modified
Page model is able to estimate the moisture content
reasonably over most of the drying time.

The moisture diffusivity values for kale were calcu-

lated from the drying data and constant B of Eq.

(7)

.

The moisture diffusivity values calculated using this
equation ranged from 14.8894

· 10

10

m

2

/s to 55.9451

·

10

10

m

2

/s and therefore fall within the range of

0.8

· 10

13

to 64.6

· 10

10

m

2

/s reported by

Doulia et al.

(2000)

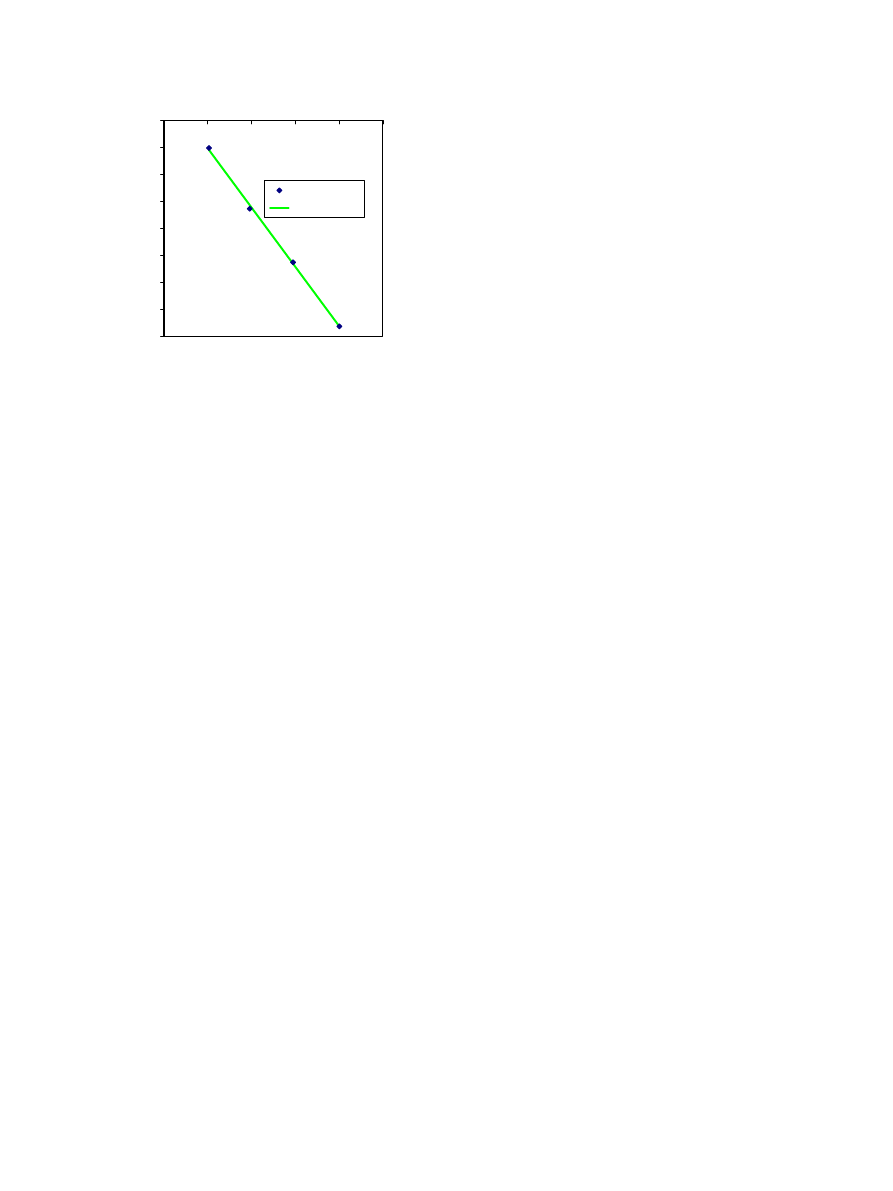
. The diffusivity constant also had an Arrhenius-

type relationship with absolute temperature with a high
R

2

of 0.9989 as depicted in

Fig. 8

. The activation energy

for kale was also computed and found to be 36.115 kJ/

mol which is within the range of 12.87–58.15 kJ/mol
reported by

Senadeera et al. (2003)

for other high mois-

ture vegetables.

Table 1
Coefficients of the Newton, Henderson and Pabis, Page and Modified Page models following the non-linear regression of moisture ratio data for kale
dried in 10 mm depth layers

Model

T (

C)

K (min

1

)

a

n

R

2

Newton MR = exp(

kt)

30

0.0093

0.9949

40

0.0149

0.9951

50

0.0222

0.9882

60

0.0349

0.9949

Henderson and Pabis MR = a exp(

kt)

30

0.0091

1.0403

0.9954

40

0.0144

1.1001

0.9974

50

0.0192

1.1366

0.9922

60

0.0349

1.0029

0.9948

Page MR = exp(

kt

n

)

30

0.0152

0.9067

0.9976

40

0.0257

0.8941

0.9985

50

0.0279

0.8832

0.9963

60

0.0342

1.0051

0.9950

Modified Page MR = exp(

kt)

n

30

0.0099

0.9067

0.9976

40

0.0167

0.8941

0.9985

50

0.0174

0.8832

0.9963

60

0.0348

1.0051

0.9950

Table 2
Equations of the correlation of the drying rate constants with drying air temperature and coefficients of determination (R

2

) and standard error of

estimate (SEE) for drying air temperatures in the range of 30–60

C

Model

Equation

R

2

SEE

Newton

k = exp(9.8446

4400.6/T

abs

)

0.9954

0.0203

Henderson and Pabis

a = 0.897459, k = exp(9.6159

4343.9/T

abs

)

0.9947

0.0216

Page

n = 0.894653, k = exp(4.3412

2553.7/T

abs

)

0.9853

0.0424

Modified Page

n = 0.894653, k = exp(8.0487

3836.1/T

abs

)

0.9961

0.0199

0

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

1

0

100

200

300

400

500

Time, minutes

M

o

is

ture ratio

exp 30˚C

exp 40˚C

exp 50˚C

exp 60˚C

est 30˚C

est 40˚C

est 50˚C

est 60˚C

Fig. 7. Comparison of experimental alues of moisture ratio and those
estimated using Modified Page model in the air temperature range of
30–60

C.

G. Mwithiga, J.O. Olwal / Journal of Food Engineering 71 (2005) 373–378

377

4. Conclusions

Sliced kale could be successively dried in a connective

air dryer in thin layers ranging from 10 mm to 50 mm
although the drying time considerably increased when
the layer thickness exceed 20 mm. Increasing the temper-
ature of drying air from 30 to 50

C reduced the drying

time by half for all drying depths. All the drying models
considered in this study could adequately represent the
drying behaviour of kale, although the Modified Page
model was better than the other three models. The mois-
ture diffusivity of kale was found to range between
14.9

· 10

10

and 55.9

· 10

10

m

2

/s within the tempera-

ture range of 30–60

C and it could be represented in

an Arrhenius-type relationship with good accuracy.
The activation energy was also found to be 36.115 kJ/
mol.

References

Akpinar, E. K., Bicer, Y., & Midili, A. (2003). Modeling and

experimental study on drying of apple slices in a convective
cyclone dryer. Journal of Food Process Engineering, 26(6), 515–543.

ASAE (1997). ASAE Standards 1997. St Josephs MI, USA: America

society of agricultutral engineers.

Cao, W., Nishiyama, Y., Koide, S., & Lu, H. Z. (2004). Drying

enhancement of rough rice by electric field. Biosystems Engineering,
87(4), 445–451.

Demir, V., Gunhan, T., Yagcioglu, A. K., & Degirmencioglu, A.

(2004). Mathematical modeling and the determination of some
quality parameters of air-dried bay leaves. Biosystems Engineering,
88(3), 325–335.

Doulia, D., Tizia, K., & Gekas, G. (2000). A knowledge base for

apparent mass diffusivity coefficient (D

eff

) of foods: Physical

properties of food database. Nelfood.com., Available from:

http://

www.nelfood.com

.

Doymaz, I. (2004a). Drying kinetics of white mulberry. Journal of Food

Engineering, 61(3), 341–346.

Doymaz, I. (2004b). Pretreatment effect on sun drying of mulberry

fruit (Morus alba L.). Journal of Food Engineering, 65(2), 205–209.

Doymaz, I. (2004c). Convective air drying characteristics of thin layer

carrots. Journal of Food Engineering, 61(3), 359–364.

Gaston, A. L., Abalone, R. M., Giner, S. A., & Bruce, D. M. (2004).

Effect of modelling assumptions on the effective water diffusivity in
wheat. Biosystems Engineering, 88(2), 175–185.

Imungi, J.K., (1992). Postharvest handling of perishable crops. In

Proceedings of the postharvest management of food crops seminar
held in serena hotel. Jomo Kenyatta University of Agriculture and
Technology, Nairobi.

Karekezi, S., & Ranja, T. (1997). Renewable energy technologies in

Africa. London and New Jersey: Zed books Ltd.

Krokida, M. K., Foundoukidis, E., & Maroulis, Z. (2004). Drying

constants: Literature data compilation for food-stuffs. Journal of
Food Engineering, 61(3), 321–330.

Lahsansi, S., Kouhila, M., Mahrouz, M., & Jaouhari, J. T. (2004a).

Drying kinetics of prickly pear fruit (Opuntia Fiscus indica). Journal
of Food Engineering, 61(2), 173–179.

Lahsansi, S., Kouhila, M., Mahrouz, M., Mohamed, A., & Agorram,

B. (2004b). Characteristic drying curve and mathematical modeling
of thin layer drying of prickly pear cladode (Opuntia Fiscus indica).
Journal of Food Process Engineering, 27(2), 103–107.

MaCabe, W. L., Smith, J. C., & Harriott, P. (1993). Unit operations of

chemical engineering (5th ed.). Singapore: McGraw-Hill Book Co,
pp. 781–784.

OÕcallaghan, J. R., Menzzies, D. J., & Bailey, P. H. (1974). Digital

simulation of agricultural drier performance. Journal of Agricul-
tural Engineering Research, 16, 223–244.

Senadeera, W., Bhandari, B. R., Young, G., & Wijesinghe, B. (2003).

Influence of shape of selected vegetable materials on drying kinetics
during fluidized bed drying. Journal of Food Engineering, 58(3),
277–283.

Sharma, G. P., & Prasad, S. (2004). Effective moisture diffusivity of

garlic cloves undergoing microwave convective drying. Journal of
Food Engineering, 65(4), 609–617.

Simal, S., Femenia, A., Garau, M. C., & Rossello, C. (2005). Use of

exponential, Page and diffusion models to simulate the drying
kinetics of kiwi fruit. Journal of Food Engineering, 66(3), 323–328.

Sogi, D. S., Shivhare, U. S., Garg, S. K., & Bawa, S. A. (2003). Water

sorption isotherms and drying characteristics of tomato seeds.
Biosystems Engineering, 84(3), 297–301.

Togrul, I. T., & Pehlivan, D. (2004). Modeling of thin layer drying

kinetics of some fruits under open air sun drying process. Journal of
Food Engineering, 65(3), 413–425.

Velic´, D., Planinic´, M., Thomas, S., & Bilic´, M. (2004). Influence of

air-flow velocity on kinetics of convection apple drying. Journal of
Food Engineering, 64(1), 97–102.

Waithaka, L. (1992). Storage of horticultural crops. In Proceedings of

the postharvest management of food crops seminar held in serena
hotel. Jomo Kenyatta University of Agriculture and Technology,
Nairobi.

-20.

4

-20.

2

-20

-19.

8

-19.

6

-19.

4

-19.

2

-19

-18.

8

2. 90

3. 00

3. 10

3. 20

3. 30

3. 40

1/Tabs . 10

3

ln D

V

ln Dv

Linear (ln Dv)

Fig. 8. Logarithm of thermal diffusivity as a function of the invers of
absolute temperature.

378

G. Mwithiga, J.O. Olwal / Journal of Food Engineering 71 (2005) 373–378