Matematyka A, kolokwium, 5 grudnia 2007, 18:10 — 19:40

Uzupe lni lem rozwiazanie zadania piatego 2 stycznia 2008.

1. (5 pt.)

Znale´z´c granice lim

n→∞

7n!−3n

n

+5n

2

·2007

n

−2n!+13n

n

+11n·2007

n

lub wykaza´c, ˙ze ta granica nie istnieje.

Rozwiazanie:

Poniewa˙z 0 <

n!

n

n

=

1

n

·

2

n

·

3

n

· . . . ·

n−1

n

·

n
n

≤

1

n

, wiec lim

n→∞

n!

n

n

= 0 . Je´sli

n >

6000 , to 0 <

n

2

2007

n

n

n

= 2007

2

·

2007

n

n−2

<

4028014·

1
2

n−2

= 16112056·

1
2

n

−−−−→

n→∞

0 ,

zatem lim

n→∞

n

2

2007

n

n

n

= 0 . Poniewa˙z 0 <

n·2007

n

n

n

≤

n

2

2007

n

n

n

, wiec r´

ownie˙z lim

n→∞

n·2007

n

n

n

= 0 .

Wobec tego

lim

n→∞

7n! − 3n

n

+ 5n

2

· 2007

n

−2n! + 13n

n

+ 11n · 2007

n

= lim

n→∞

7 ·

n!

n

n

− 3 + 5 ·

n

2

2007

n

n

n

−2 ·

n!

n

n

+ 13 + 11 ·

n·2007

n

n

n

=

=

7 · 0 − 3 + 5 · 0

−2 · 0 + 13 + 11 · 0

=

−3

13

.

2. (5 pt.)

Znale´z´c granice lim

n→∞

ln(n

27

+n−cos n)

ln(n

10

+5n+sin n

n

)

lub wykaza´c, ˙ze ta granica nie istnieje.

Wyja´sni´c, czy istnieje taka liczba naturalna k > 1 , ˙ze dla ka˙zdej liczby naturalnej

n > k

zachodzi nier´

owno´s´c

ln(n

27

+n−cos n)

ln(n

10

+5n+sin n

n

)

>

10 .

Rozwiazanie:

0 ≤

cos n

n

27

≤

1

n

27

≤

1

n

−−−−→

n→∞

0 , 0 ≤

sin n

n

n

10

≤

1

n

10

≤

1

n

−−−−→

n→∞

0 . Wobec tego

lim

n→∞

ln(n

27

+ n − cos n)

ln(n

10

+ 5n + sin n

n

)

= lim

n→∞

ln n

27

+ ln(1 +

1

n

26

−

cos n

n

27

)

ln n

10

+ ln(1 +

5

n

9

−

sin n

n

n

10

)

=

= lim

n→∞

27 ln n + ln(1 +

1

n

26

−

cos n

n

27

)

10 ln n + ln(1 +

5

n

9

−

sin n

n

n

10

)

= lim

n→∞

27 +

ln(1+

1

n

26

−

cos n

n

27

)

ln n

10 +

ln(1+

5

n

9

−

sin nn

n

10

)

ln n

=

27 +

ln(1+0−0)

∞

10 +

ln(1+0−0)

∞

=

27
10

.

Z definicji granicy ciagu wynika wiec, ˙ze istnieje taka liczba naturalna n

0

, ˙ze dla ka˙zdej

liczby naturalnej n > n

0

zachodzi nier´

owno´s´c

ln(n

27

+n−cos n)

ln(n

10

+5n+sin n

n

)

−

27
10

<

3

10

, a z niej wynika, ˙ze

ln(n

27

+n−cos n)

ln(n

10

+5n+sin n

n

)

−

27
10

<

3

10

, wiec

ln(n

27

+n−cos n)

ln(n

10

+5n+sin n

n

)

<

27
10

+

3

10

= 3 < 10 .

3. Niech a

n

=

1

3n+1

+

1

3n+4

+

1

3n+7

+ · · · +

1

6n−2

.

(2 pt.)

Obliczy´c a

1

, a

2

i a

3

i wypisa´c je w kolejno´sci malejacej.

(8 pt.)

Wykaza´c, ˙ze ciag (a

n

) ma sko´

nczona granice i ˙ze ta granica jest r´

o˙zna od 0 .

Rozwiazanie:

Poniewa˙z 3 · 1 + 1 = 4 = 6 · 1 − 2 , wiec a

1

jest suma jednego sk ladnika: a

1

=

1
4

.

a

2

=

1

3·2+1

+

1

3·3+1

=

1
7

+

1

10

=

17
70

<

17
68

=

1
4

= a

1

. a

3

=

1

3·3+1

+

1

3·4+1

+

1

3·5+1

=

1

10

+

1

13

+

1

16

=

=

104+80+65

1040

=

249

1040

<

250

1040

=

25

104

=

1750
7280

<

1768
7280

=

17
70

= a

2

. Trzy pierwsze wyrazy ciagu w

kolejno´sci malejacej to a

1

=

1
4

, a

2

=

17
70

i a

3

=

25

104

.

Jasne jest, ˙ze liczba a

n

jest suma n sk ladnik´

ow: r´

o˙znica mianownik´

ow jest r´

owna 3 , za-

czynamy od 3n + 1 i ko´

nczymy na 6n − 2 , wiec tych mianownik´ow jest 1 +

6n−2−(3n+1)

3

=

=1 +

3n−3

3

= 1 + n − 1 = n . Najmniejszym sk ladnikiem tej sumy jest

1

6n−2

, wiec a

n

≥

n ·

1

6n−2

> n ·

1

6n

=

1
6

. Je´

sli wiec ciag (a

n

) ma granice, to nie jest ona mniejsza ni˙z

1
6

. Mamy

a

n+1

=

1

3(n+1)+1

+

1

3(n+1)+4

+

1

3(n+1)+7

+· · ·+

1

6n−2

+

1

6n+1

+

1

6n+4

(oczywi´scie 6n+4 = 6(n+1)−2 ).

Wynika stad, ˙ze

a

n+1

− a

n

=

1

6n+1

+

1

6n+4

−

1

3n+1

=

1

6n+1

−

1

6n+2

+

1

6n+4

−

1

6n+2

=

1

(6n+1)(6n+2)

−

2

(6n+4)(6n+2)

=

=

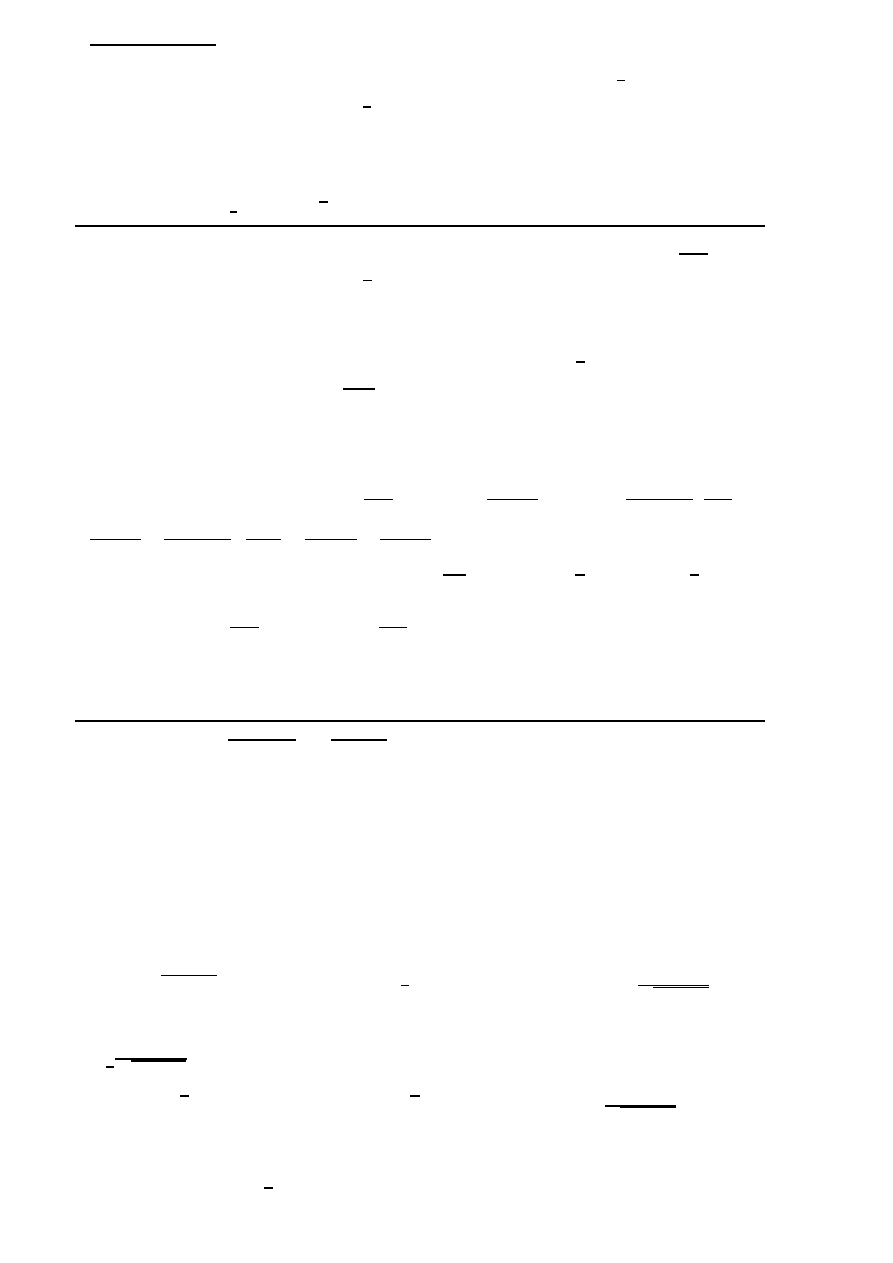
−6n+2

(6n+1)(6n+2)(6n+4)

<

0 . Wykazali´smy, ˙ze a

n+1

< a

n

dla n = 1, 2, 3, . . . . Oznacza to, ˙ze ciag

(a

n

) jest ´sci´sle malejacy, a poniewa˙z wszystkie jego wyrazy sa wieksze od

1
6

, wiec ma granice i

jest nia jaka´s liczba wieksza lub r´

owna

1
6

.

Je´sli cz lowiek troche sie pomeczy z r´

o˙znymi nier´

owno´sciami, kt´

ore wystepowa ly na zajeciach,

to mo˙ze te granice znale´z´c, ale zapewne nie w czasie kolokwium (z powodu braku czasu). W dal-

szej cze´sci wyk ladu pojawi sie twierdzenie, dzieki kt´

oremu mo˙zna bedzie znale´z´c ja dosy´c szybko.

Zdradze jej warto´s´c:

1
3

ln 2 = ln

3

√

8 ≈ 0,2310490602 .

4. (10 pt.) Znale´z´c pochodne nastepujacych funkcji: x

sin 2x

, arctg(cos x)+arctg(

1

cos x

) okre´s-

lonych na przedziale (0,

π

4

) .

Rozwiazanie:

Mamy x

sin 2x

0

= e

ln x·sin 2x

0

pochodna

=======

z lo˙zenia

e

ln x·sin 2x

ln x · sin 2x

0

pochodna

=======

iloczynu

= x

sin 2x 1

x

· sin 2x + ln x · 2 cos 2x

.

Przypomnijmy, ˙ze (arctg x)

0

=

1

1+x

2

— by lo na wyk ladzie, wynika te˙z latwo z wzoru na

pochodna funkcji z lo˙zonej: x = tg(arctg x) , wiec

1 = (x)

0

= tg(arctg x)

0

pochodna

=======

z lo˙zenia

1 + tg

2

(arctg x)

· (arctg x)

0

= [1 + x

2

] · (arctg x)

0

.

Mamy teraz

arctg(cos x) + arctg(

1

cos x

)

0

pochodna

=======

z lo˙zenia

1

1+cos

2

x

· (cos x)

0

+

1

1+1/ cos

2

x

1

cos x

0

=

=

− sin x

1+cos

2

x

+

1

1+1/ cos

2

x

·

sin x

cos

2

x

=

− sin x

1+cos

2

x

+

sin x

1+cos

2

x

= 0 . Wynik mo˙zna by lo uzyska´c bez ˙zadnych

rachunk´

ow. Mo˙zna by lo zauwa˙zy´c, ˙ze je´sli tg α =

1

tg β

i 0 ≤ α, β <

π

2

, to α + β =

π

2

, starczy

przypomnie´c sobie definicje funkcji trygonometrycznych. U nas α = arctg(cos x) , wtedy tg α =

cos x oraz β = arctg(

1

cos x

) , zatem tg β =

1

cos x

. R´

o˙zniczkowali´smy wiec funkcje sta la. Oczywi´scie

na poczatku nauki szanse na to, ˙ze kto´s pomy´sli o takim rozwiazaniu sa minimalne, na to ma

szanse tylko kto´s, kto ma spora wprawe i kto ma zwyczaj zastanawia´c sie nad tym, czy rachunk´

ow

nie mo˙zna jako´s omina´c.

5. Niech f (x) =

3

px(3 − x

2

) =

3

√

3x − x

3

.

(3 pt.)

W jakich punktach funkcja f nie ma sko´

nczonej pochodnej (tzn. jest nier´

o˙znicz-

kowalna)? Odpowied´z nale˙zy uzasadni´c.

(4 pt.)

Znale´z´c przedzia ly, na kt´

orych funkcja f jest ´sci´sle rosnaca, na kt´

orych jest ´sci´sle

malejaca.

(3 pt.)

Korzystajac z uzyskanych rezultat´

ow naszkicowa´c wykres funkcji f . Nie bada´c

wypuk lo´sci, nie szuka´c asymptot . . .

Rozwiazanie:

Mamy (zn´

ow ´cwiczymy pochodna z lo˙zenia)

f

0

(x) =

3

√

3x − x

3

0

=

3x − x

3

1/3

0

=

1
3

· 3x − x

3

−2/3

· (3 − 3x

2

) =

1−x

2

3

√

(3x−x

3

)

2

. Jasne

jest, ˙ze mianownik jest zawsze nieujemny, wiec nie ma wp lywu na znak pochodnej. Mamy te˙z

lim

x→

√

3

1−x

2

3

√

(3x−x

3

)

2

= −∞ , bo licznik da ˙zy do −2 , a mianownik jest dodatni i da ˙zy do 0 . Wo-

bec tego f

0

(

√

3) = −∞ . Analogicznie f

0

(−

√

3) = −∞ . Mamy te˙z lim

x→0

1−x

2

3

√

(3x−x

3

)

2

= ∞ , wiec

f

0

(0) = +∞ . Pochodna jest dodatnia, na przedziale (−1, 1) , wiec funkcja jest ´sci´sle rosnaca

na przedziale [−1, 1] . Na ka˙zdej z p´o lprostych (−∞, −1) , (1, ∞) pochodna jest ujemna (to
dotyczy te˙z punkt´

ow ±

√

3 , w kt´

orych pochodna nie jest sko´

nczona!), wiec funkcja jest ´sci´sle

malejaca na ka˙zdej z p´

o lprostych (−∞, −1] , [1, ∞) . Mo˙zna jeszcze zauwa˙zy´c, ˙ze f(−1) = −

3

√

2

i f (1) =

3

√

2 ≈ 1,26 . Oczywi´scie przybli˙zanie liczby

3

√

2 w czasie kolokwium wymagane nie by lo,

istotne by lo jedynie to, ˙ze

3

√

2 > 1 , co ka˙zdy student widzi natychmiast.

6. (3 pt.)

Przez punkty A = (1, 8) i X = (x, 0) , gdzie x > 1 , przechodzi prosta, kt´

ora

przecina o´s OY w punkcie Y = (0, y) . Wyznaczy´c liczbe y w zale˙zno´sci od

wsp´

o lrzednej x punktu X .

(7 pt.)

Niech X i Y oznaczaja punkty opisane w poprzedniej cze´sci zadania. Znale´z´c

najkr´

otszy z odcink´

ow XY .

Rozwiazanie:

Niech O = (0, 0) , B = (1, 0) . Tr´

ojkaty ABX i Y OX sa podobne (Szanowny

Czytelniku, trzeba sobie narysowa´c co´s na kartce!), wiec

AB

BX

=

Y O

OX

, czyli

8

x−1

=

y
x

. Stad

y

=

8x

x−1

=

8(x−1)+8

x−1

= 8 +

8

x−1

. Niech d(x) =

px

2

+ y

2

=

q

x

2

+ (8 +

8

x−1

)

2

i niech f (x) =

= d(x)

2

= x

2

+ (8 +

8

x−1

)

2

. Znajdziemy najmniejsza warto´s´c funkcji f , a potem znajdziemy

pierwiastek z tego wyniku, czyli najmniejsza warto´s´c funkcji d . Tak wolno postapi´c, bo im

wieksza liczba podpierwiastkowa, tym wiekszy pierwiastek z niej. Obliczamy pochodna: f

0

(x) =

=2x + 2(8 +

8

x−1

) ·

−8

(x−1)

2

= 2x − 2 ·

8x

x−1

·

8

(x−1)

2

= 2x 1 −

64

(x−1)

3

. Ta pochodna jest r´owna 0

wtedy i tylko wtedy, gdy x − 1 = 4 — interesuja nas wy lacznie liczby x > 1 ! Jasne jest, ˙ze je´sli
x >

5 , to f

0

(x) > 0 , zatem na p´

o lprostej [5, ∞) funkcja f jest ´sci´sle rosnaca. Je´sli 1 < x < 5 ,

to f

0

(x) < 0 , a z tego wynika, ˙ze na przedziale (1, 5] funkcja f jest ´sci´sle malejaca. Z tych dw´

och

zda´

n wnioskujemy, ˙ze najmniejsza warto´s´c funkcja f przyjmuje w punkcie 5 . Ta najmniejsza

warto´s´c r´

owna jest 5

2

+ 8 +

8

5−1

2

= 125 . Wobec tego najkr´

otszy z odcink´

ow, kt´

orymi byli

zmuszeni sie Pa´

nstwo interesowa´c w czasie kolokwium ma d lugo´s´c

√

125 = 5

√

5 ; jego ko´

ncami

sa punkty (5, 0) i (0, 10) .