88 Â

WIAT

N

AUKI

Sierpieƒ 1999

J

eden z uroków matematyki polega
na tym, ˝e niektóre proste zagadnie-
nia potrafià przez stulecia sprawiaç

k∏opot najwybitniejszym umys∏om Êwia-
ta. Za przyk∏ad niech pos∏u˝à Wielkie
Twierdzenie Fermata, hipoteza Keple-
ra czy zagadnienie czterech barw –
wszystkie rozwiàzano dopiero w ostat-
nich kilku dziesi´cioleciach. Uwag´ wie-
lu matematyków amatorów przyciàga-
∏o szczególnie zagadnienie czterech
barw i w pewnym sensie szkoda, ˝e zo-
sta∏o rozwiàzane, bo wysch∏o niewy-
czerpane êród∏o zabawy. Post´p jest
ogromny, mog∏oby si´ wi´c wydawaç,
˝e nie ma ju˝ interesujàcych wyzwaƒ
dla amatorów, ale jak zobaczymy, nie
jest to prawdà.

Zacznijmy od zagadnienia czterech

barw postawionego oko∏o 150 lat temu.
Zgodnie z hipotezà wystarczà cztery
barwy, by pokolorowaç ka˝dà p∏askà
map´ tak, aby ˝adne dwa przylegajàce
do siebie kraje nie by∏y pomalowane jed-
nakowo. Udowodnili to w 1976 roku,
posi∏kujàc si´ obliczeniami komputero-
wymi, Kenneth Appel i Wolfgang Ha-
ken z University of Illinois. Twierdze-
nie o czterech barwach, jak si´ je teraz
nazywa, nale˝y do ga∏´zi matematyki
zwanej teorià grafów. Graf jest zbio-
rem „wierzcho∏ków” reprezentowanych
przez kropki, po∏àczonych „kraw´dzia-
mi” reprezentowanymi przez linie.
Dwuwymiarowà map´ mo˝na naryso-
waç w postaci grafu – po prostu zazna-

czajàc ka˝dy kraj jako wierzcho∏ek i ∏à-
czàc kraw´dziami wierzcho∏ki repre-
zentujàce kraje sàsiednie. Zagadnienie
czterech barw sprowadza si´ wi´c do
pytania o mo˝liwoÊç pomalowania
wierzcho∏ków odpowiedniego grafu.

Teoria grafów jest êród∏em wielu py-

taƒ, które ∏atwo sformu∏owaç, ale na
które bardzo trudno udzieliç odpowie-
dzi. Wiele z nich dotyczy liczby prze-
ci´ç grafu – najmniejszej liczby przeci´ç
dwu kraw´dzi dla zadanej liczby wierz-
cho∏ków grafu. (We wszystkich punk-
tach poza wierzcho∏kami mogà przeci-
naç si´ tylko dwie kraw´dzie.) W roku
1970 matematycy Paul Erdös i Richard
K. Guy napisali: „Niemal wszystkie py-
tania dotyczàce liczby przeci´ç, któ-
re mo˝na zadaç, pozostajà bez odpo-
wiedzi.” Ta uwaga jest prawdziwa
i dziÊ. Bardzo trudno udowodniç ja-
kieÊ twierdzenie o liczbie przeci´ç, ale

matematycy amatorzy mogà znaleêç
wiele przyjemnoÊci w eksperymen-
tach z ró˝nymi grafami i dà˝yç do zre-
dukowania liczby przeci´ç. Niewyklu-
czone, ˝e takie eksperymenty pozwolà
obaliç pewne s∏ynne hipotezy, wskazu-
jàc graf o liczbie przeci´ç mniejszej ni˝
spodziewana.

Grafy o zerowej liczbie przeci´ç opi-

suje w pe∏ni twierdzenie udowodnione
przez polskiego matematyka Kazimie-
rza Kuratowskiego i okreÊlane jego na-
zwiskiem. Grafy te sà p∏askie: kraw´-
dzie ∏àczàce wierzcho∏ki nie przecinajà
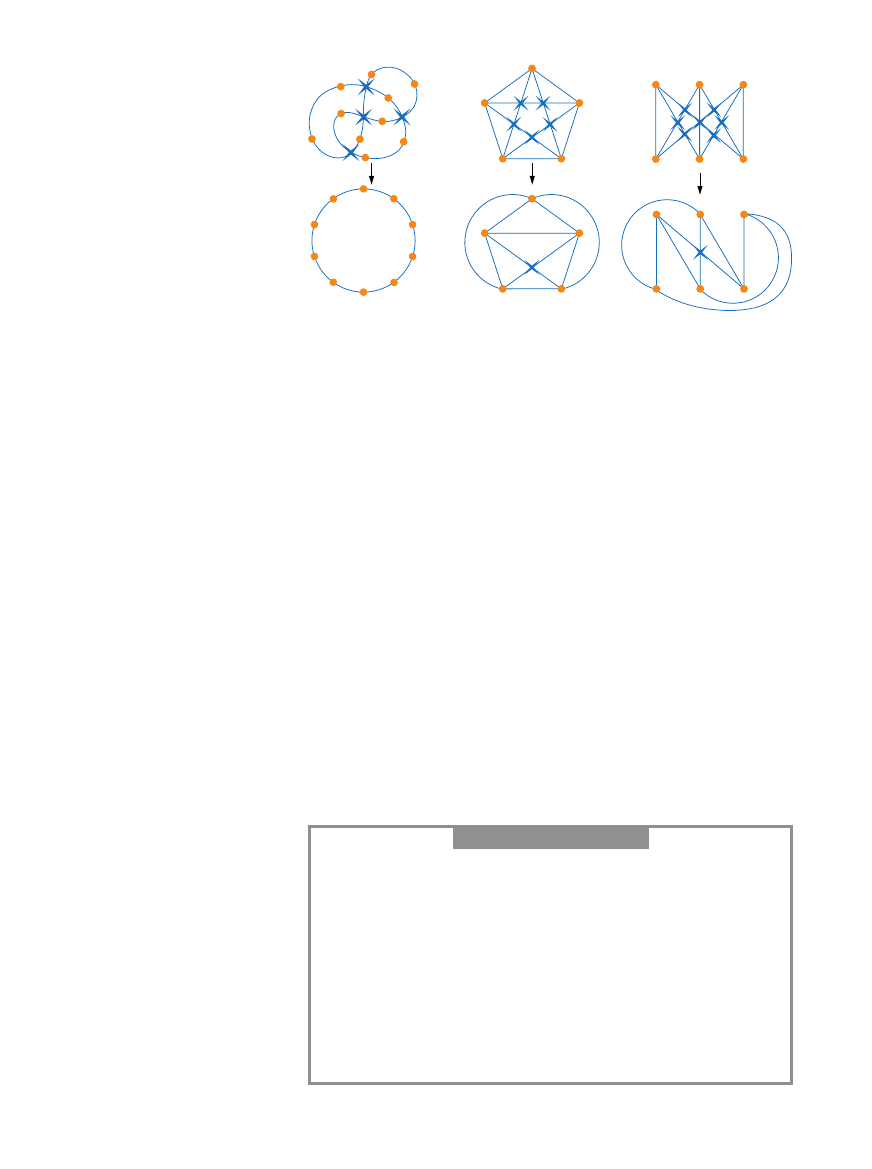
si´ w ogóle. Rozwa˝my pierwszy graf
z nast´pnej strony, w którym 10 kraw´-
dzi ∏àczy 10 wierzcho∏ków. Co prawda
kraw´dzie przecinajà si´ cztery razy,
ale graf jest p∏aski, poniewa˝ mo˝na po-
przesuwaç jego wierzcho∏ki i kraw´dzie
w taki sposób, aby wierzcho∏ki utwo-
rzy∏y pierÊcieƒ – wtedy przeci´cia kra-
w´dzi zniknà. Jest to graf cykliczny o 10
wierzcho∏kach, oznaczany symbolem
C

10

. Podobne grafy o n wierzcho∏kach

oznaczamy jako C

n

.

Rozwa˝my teraz drugi graf, nazywa-

ny grafem pe∏nym o pi´ciu wierzcho∏-
kach. Dziesi´ç kraw´dzi w tym grafie
∏àczy ka˝dy z wierzcho∏ków ze wszyst-
kimi pozosta∏ymi. Graf ten oznacza si´
symbolem K

5

, a analogiczne grafy pe∏-

ne o n wierzcho∏kach – K

n

. K

5

nie jest

p∏aski – niezale˝nie od tego, jak b´dzie-
my przesuwaç jego wierzcho∏ki i kra-
w´dzie, zawsze wystàpi co najmniej jed-
no przeci´cie. Liczba przeci´ç K

5

jest

zatem równa jeden.

REKREACJE MATEMATYCZNE

Ian Stewart

Skrzy˝owania torów w cegielni

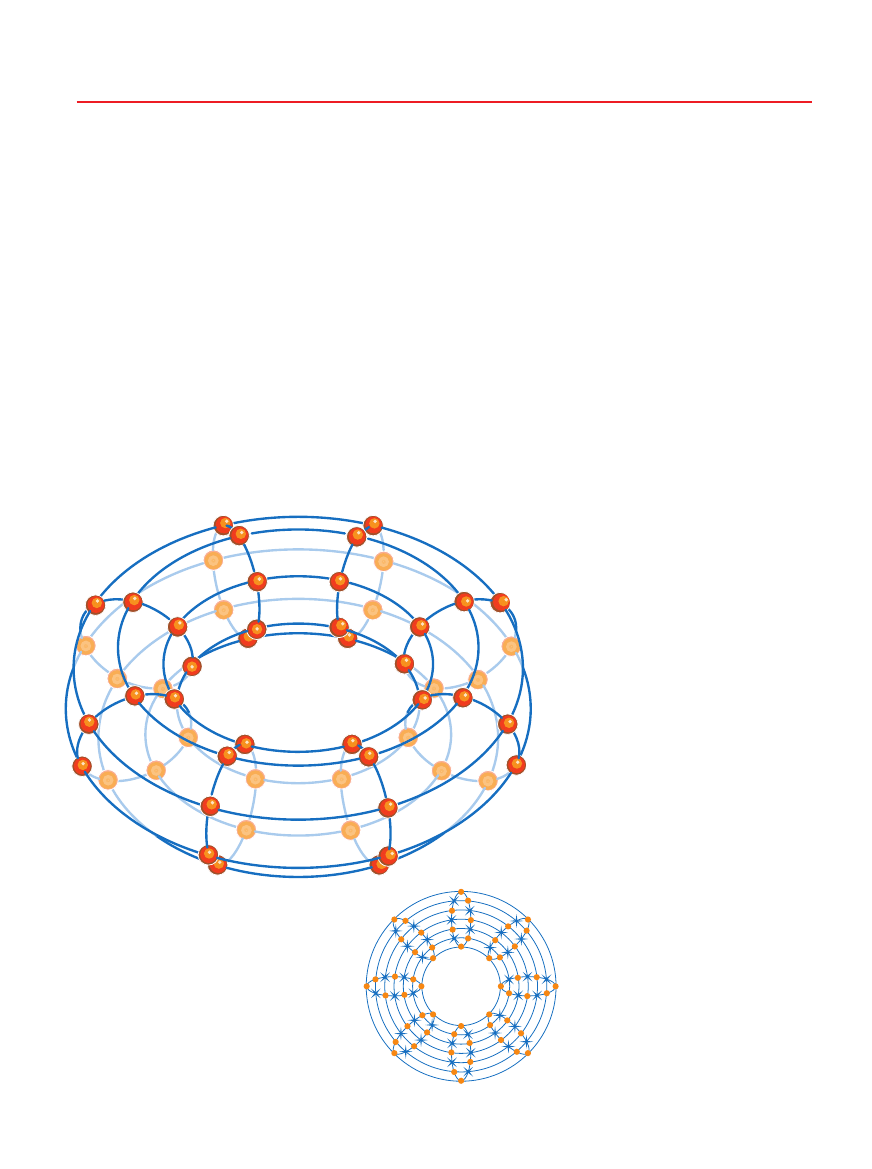
GRAF SIATKI NA TORUSIE ma osiem

okr´gów pionowych i siedem poziomych.

Na torusie nie ma przeci´ç (a), ale po

zrzutowaniu grafu na p∏aszczyzn´

przeci´ç jest 40 (b).

BRYAN CHRISTIE

a

b

Â

WIAT

N

AUKI

Sierpieƒ 1999 89

Trzeci graf jest przyk∏adem pe∏nego

grafu dwudzielnego. Sk∏ada si´ on
z dwóch trójek wierzcho∏ków, a ka˝dy
wierzcho∏ek z jednej trójki jest po∏àczo-
ny z ka˝dym wierzcho∏kiem z drugiej.
Ten graf ma symbol K

3,3

i liczb´ prze-

ci´ç równà jeden. Grafy dwudzielne
oznaczamy wed∏ug nast´pujàcej regu-
∏y: jeÊli jeden zbiór wierzcho∏ków ma
m elementów, a drugi n, to graf taki
oznaczamy K

m,n

.

Koncepcja liczby przeci´ç powsta∏a

w roku 1944, kiedy matematyk w´gier-
ski Paul Turán pracowa∏ w cegielni pod
Budapesztem. Fabryka mia∏a kilka pie-
ców do wypalania cegie∏ oraz pewnà
liczb´ sk∏adowisk. Tory dla wagoników
do przewozu cegie∏ bieg∏y od ka˝dego
pieca do ka˝dego sk∏adowiska. Pracow-
nicy wrzucali ceg∏y na wagonik, pchali
go do miejsca sk∏adowania i roz∏ado-
wywali. Zadanie by∏o w zasadzie ∏atwe,
ale w miejscach, w których krzy˝owa-
∏y si´ tory, wózki cz´sto wypada∏y z
szyn, a ∏adunek si´ wysypywa∏.

In˝ynier prawdopodobnie by si´ za-

stanowi∏, jak przeprojektowaç skrzy˝o-
wania. Matematyk Turán myÊla∏, jak
przeprojektowaç uk∏ad szyn, by otrzy-
maç najmniejszà mo˝liwà liczb´ skrzy-
˝owaƒ. Po kilku dniach wiedzia∏ ju˝, ˝e
pewne skrzy˝owania w tej akurat fabry-
ce by∏y niepotrzebne. Ale problem ogól-
ny nie przestawa∏ go intrygowaç. Dla
m pieców i n sk∏adowisk mo˝na go sfor-
mu∏owaç nast´pujàco: nale˝y znaleêç
liczb´ przeci´ç pe∏nego grafu dwudziel-
nego K

m,n

.

Problem ten pozostaje nadal nie roz-

wiàzany. Jak zauwa˝y∏a ostatnio w Ma-
thematical Magazine z grudnia 1998 roku
Nadine C. Myers z Hamline University,
znamy liczby przeci´ç tylko grafów
o ma∏ej liczbie wierzcho∏ków: pe∏nych
grafów K

n

, gdy n£10, oraz pe∏nych gra-

fów dwudzielnych K

m,n

, gdy 3£m£6.

Bardzo ma∏o wiemy na temat grafów
o wi´kszej liczbie wierzcho∏ków.

Jeszcze innym rodzajem grafu jest

prostokàtna siatka na torusie (matema-
tycznym modelu obwarzanka), poka-
zana na rysunku na poprzedniej stro-
nie. W grafie tym wyst´pujà dwie
rodziny okr´gów: osiem pionowych
o siedmiu wierzcho∏kach ka˝dy (ozna-
czonych symbolem C

7

) i siedem pozio-

mych o oÊmiu wierzcho∏kach (C

8

). Okr´-

gi te mo˝na narysowaç na torusie tak,
by nie by∏o przeci´ç: wszystkie okr´gi
przecinajà si´ tylko w wierzcho∏kach.
Ale jeÊli graf ten – C

7

x C

8

– zrzutujemy

na p∏aszczyzn´, ka˝dy z oÊmiu piono-
wych okr´gów b´dzie przecina∏ pozio-
me pi´ç razy, co da ∏àcznie 40 przeci´ç.

Tak samo mo˝na zrzutowaç m pozio-

mych okr´gów i n pionowych, gdy

umówimy si´, ˝e m£n. Zauwa˝amy, ˝e
ka˝dy pionowy okràg przecina naj-
bardziej wewn´trzny i najbardziej ze-
wn´trzny okràg poziomy tylko raz,
w wierzcho∏ku. Ka˝dy pionowy okràg
przecina pozosta∏e m – 2 poziome okr´-
gi dwukrotnie – raz w wierzcho∏ku, co
odpowiada rzeczywistemu przeci´-
ciu na torusie, i raz pomi´dzy wierz-
cho∏kami, co jest wynikiem rzutowa-
nia grafu na p∏aszczyzn´. Tak wi´c ka˝-
dy okràg pionowy daje m – 2 przeci´-
cia, a zatem graf ma ∏àcznie (m – 2)n
przeci´ç.

Panuje powszechne przekonanie, ˝e

jest to najmniejsza liczba przeci´ç gra-
fu w kszta∏cie siatki na torusie; innymi
s∏owy, liczba przeci´ç C

m

x C

n

jest rów-

na (m – 2)n. A jednak tej (m, n) hipote-
zy nie uda∏o si´ udowodniç. Wiadomo,
˝e jest ona prawdziwa, gdy 3£m£6
oraz dla m = n = 7. „Najmniejszym”
z nie udowodnionych przypadków
jest C

7

x C

8

. Zgodnie z hipotezà liczba

przeci´ç jest wtedy równa 40. Czy po-
trafisz narysowaç taki graf z liczbà prze-
ci´ç 39 lub mniej? JeÊli tak, to hipoteza
(m, n) oka˝e si´ fa∏szywa. Mo˝e to dziw-
ne, ale problem ten od wielu lat opiera
si´ po∏àczonym si∏om matematyków
Êwiata.

W roku 1997 Gelasio Salazar z Carle-

ton University w Ottawie udowodni∏,
˝e jeÊli liczba przeci´ç grafu C

m

x C

n

jest

mniejsza ni˝ (m – 2)n, to nie mo˝e byç
du˝o mniejsza. Jednak twierdzenie Sa-
lazara pozostawia troch´ miejsca dla
liczby przeci´ç mniejszej od postulowa-
nej w hipotezie. Hipoteza (m, n) mo˝e
równie dobrze okazaç si´ fa∏szywa, co
wyjaÊnia∏oby, dlaczego dotàd nie uda-
∏o si´ jej udowodniç. Albo byç mo˝e jest
z nià tak jak z twierdzeniem Fermata,
hipotezà Keplera czy zagadnieniem
czterech barw: jest prawdziwa, ale trud-
na do udowodnienia!

T∏umaczy∏

Tomasz ˚ak

W

„Hipotezie miechów” [Âwiat Nauki, wrzesieƒ 1998] wyjaÊni∏em, dlaczego nie
mo˝na zbudowaç wieloÊciennych miechów, czyli wieloÊcianu, który zmienia

obj´toÊç, gdy si´ zgina. Zasadniczà rol´ odgrywajà tu dwa za∏o˝enia: Êciany wie-
loÊcianu muszà pozostawaç doskonale p∏askie, a kraw´dzi nie wolno roz∏àczaç.
Karton nie jest jednak zupe∏nie sztywny, mo˝na wi´c zbudowaç model kartono-
wych miechów wieloÊciennych, które zmieniajà obj´toÊç, bo ich Êciany si´ wygi-
najà lub ich kraw´dzie oddalajà si´ od siebie.

David Briggs z Waltrop w Niemczech opatentowa∏ pomys∏owy model takich mie-

chów. Mo˝na go obejrzeç w Internecie pod adresem: www.patents.ibm.com/details?
patent_number=3993222. Wynalazca mówi, ˝e inspiracjà by∏o doÊwiadczenie z dzie-
ciƒstwa: „Gdy wycisnà∏em zbyt wiele pasty do z´bów z tuby, ojciec pokaza∏ mi, jak
wciàgnàç troch´ pasty z powrotem, Êciskajàc tubk´ inaczej, prostopadle do kie-
runku pierwszego ÊciÊni´cia.”

SPRZ¢˚ENIE ZWROTNE

TEORIA GRAFÓW obejmuje wyznaczanie minimalnej liczby przeci´ç dla ró˝nych

rodzajów grafów. Graf p∏aski (a) mo˝na tak przekszta∏ciç, aby nie mia∏ przeci´ç.

Pe∏ny graf o pi´ciu wierzcho∏kach (b) ma liczb´ przeci´ç równà jeden, podobnie

jak pe∏ny graf dwudzielny o dwóch trójkach wierzcho∏ków (c).

BRYAN CHRISTIE

b

c

a