Zad. 1.

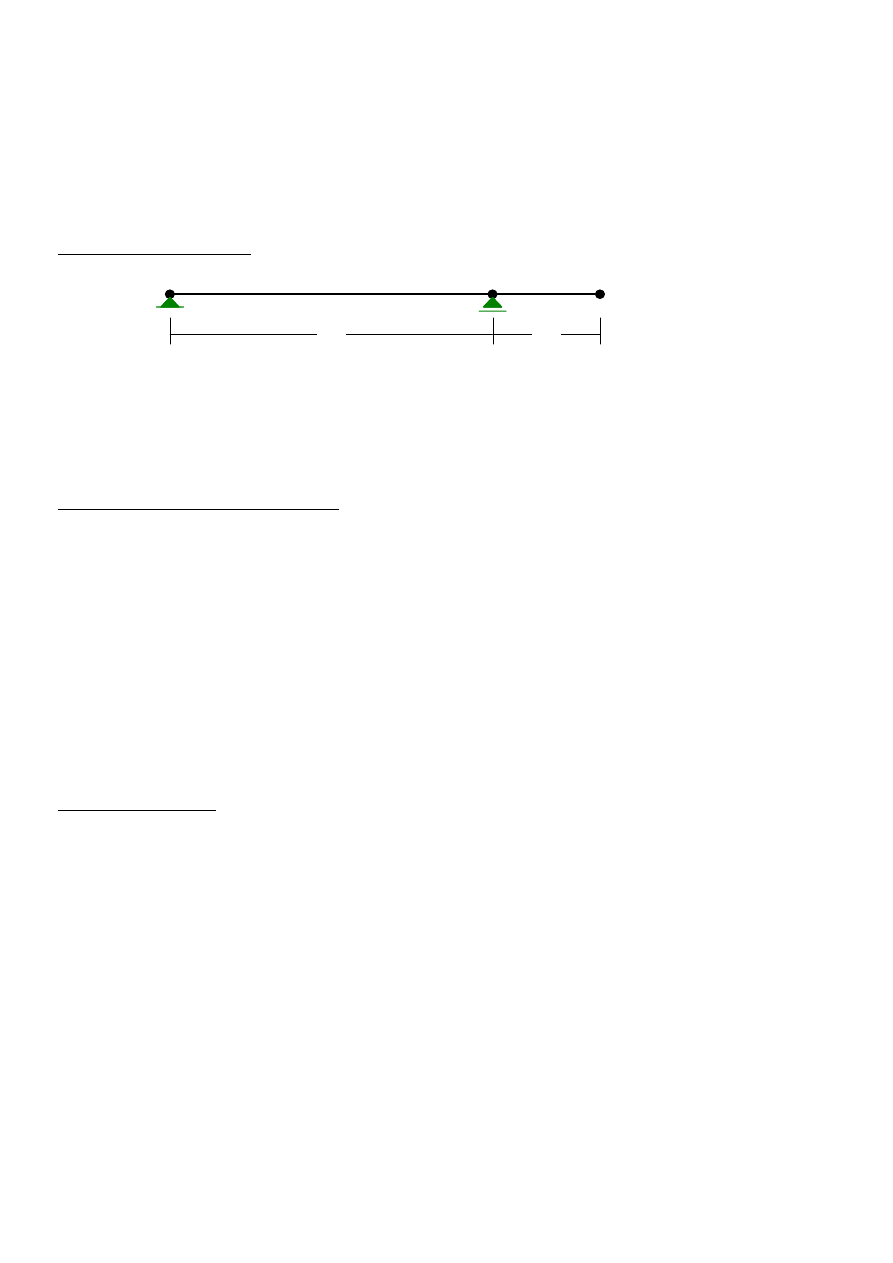
Zaprojektować zbrojenie belki o przekroju dwuteowym i schemacie statycznym pokazanym
na rysunku. Belka wykonana będzie z betonu B25 (C20/25) i zbrojona stalą klasy A-IIIN (zbrojenie
główne) oraz A-II (zbrojenie na ścinanie). Belka będzie użytkowana w środowisku o klasie
ekspozycji XC2.

1.0 Schemat statyczny

g =

4,5

kN/m

wartość obciążenia stałego

p =

8

kN/m

wartość obciążenia użytkowego o zmiennej długości

L

1

=

9

m

rozpiętość między podporami 1 i 2

L

2

=

3

m

wysięg przewieszenia

2.0 Geometria przekroju poprzecznego

b

g

=

0,35

m

szerokość półki górnej

b

s

=

0,15

m

szerokość środnika

b

d

=

0,2

m

szerokość półki dolnej

h

g

=

0,2

m

wysokość półki górnej

h

s

=

0,3

m

wysokość środnika

h

d

=

0,1

m

wysokość półki dolnej

h =

0,6

m

wysokość całego przekroju

A

c

=

0,135

m

2

=

1350

cm

2

pole przekroju elementu

3.0 Dane materiałowe

Pręty zbrojenia głównego A-IIIN:

φ

=

1,2

cm

ś

rednica pręta zbrojeniowego

A

φ

12

=

1,131

cm

2

pole przekroju pręta

f

yk

=

500

MPa

charakterystyczna granica plastyczności stali

f

yd

=

420

MPa

obliczeniowa granica plastyczności stali

ξ

eff,lim

=

0,5

[-]

Strzemiona A-II:

φ

=

0,6

cm

ś

rednica pręta zbrojeniowego

A

φ

6

=

0,283

cm

2

pole przekroju pręta

f

yk

=

355

MPa

charakterystyczna granica plastyczności stali

f

yd

=

310

MPa

obliczeniowa granica plastyczności stali

ZGINANIE I ŚCINANIE PRZEKROJÓW TEOWYCH

1

2

3

9,000

3,000

H=12,000

Beton B25 (C20/25):

f

cd

=

13,3

MPa

obliczeniowa wytrzymałość betonu na ściskanie

f

ctd

=

1

MPa

obliczeniowa wytrzymałość betonu na rozciąganie

f

ck

=

20

MPa

charaktrystyczna wytrzymałość betonu na ściskanie

f

ctm

=

2,2

MPa

ś

rednia wytrzymałość betonu na rozciąganie

4.0 Wartości sił wewnętrznych

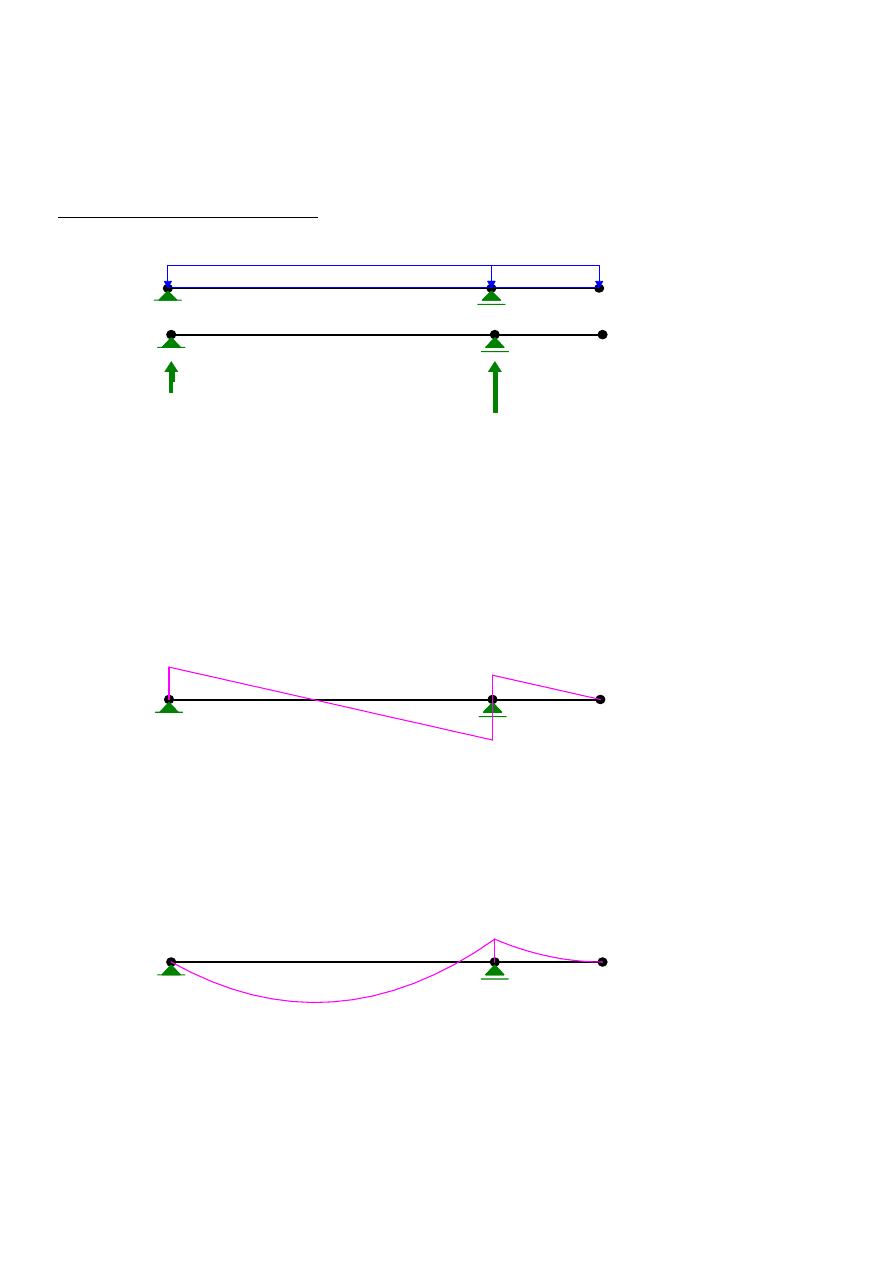
4.1 Obciążenie stałe

~ Wyznaczenie reakcji od obciążenia stałego g

Σ

M

A

= 0

R

B

*L

1

- g(L

1

+L

2

)*0,5*(L

1

+ L

2

) = 0

R

B

= 0,5 g (L

1

+ L

2

)

2

/L

1

R

B

=

36

kN

Σ

Y = 0

R

A

- g(L

1

+ L

2

) + R

B

= 0

R

A

= g (L

1

+ L

2

) - R

B

R

A

=

18

kN

~ Wykres sił tnących

T [kN]

~ Określenie położenia maksymalnego momentu przęsłowego (zerowanie się sił tnących)

Z twierdzenia Talesa: 18 / x = (18 + 22,5) / L

1

x =

4

m

~ Wykres momentów zginających

M [kNm]

~ Maksymalne momenty od obciążenia stałego g

* przęsłowy M

max

= R

A

* x - g * x * 0,5 x =

36

kNm

* podporowy

M

min

= -g * L

2

* 0,5 L

2

=

-20,25

kNm

1

2

4,500

4,500

4,500

4,500

1

2

3

18,000

R

A

R

B

1

2

18,000

-22,500

18,000

-22,500

13,500

13,500

1

2

-20,250

35,998

-20,250 -20,250

-20,250

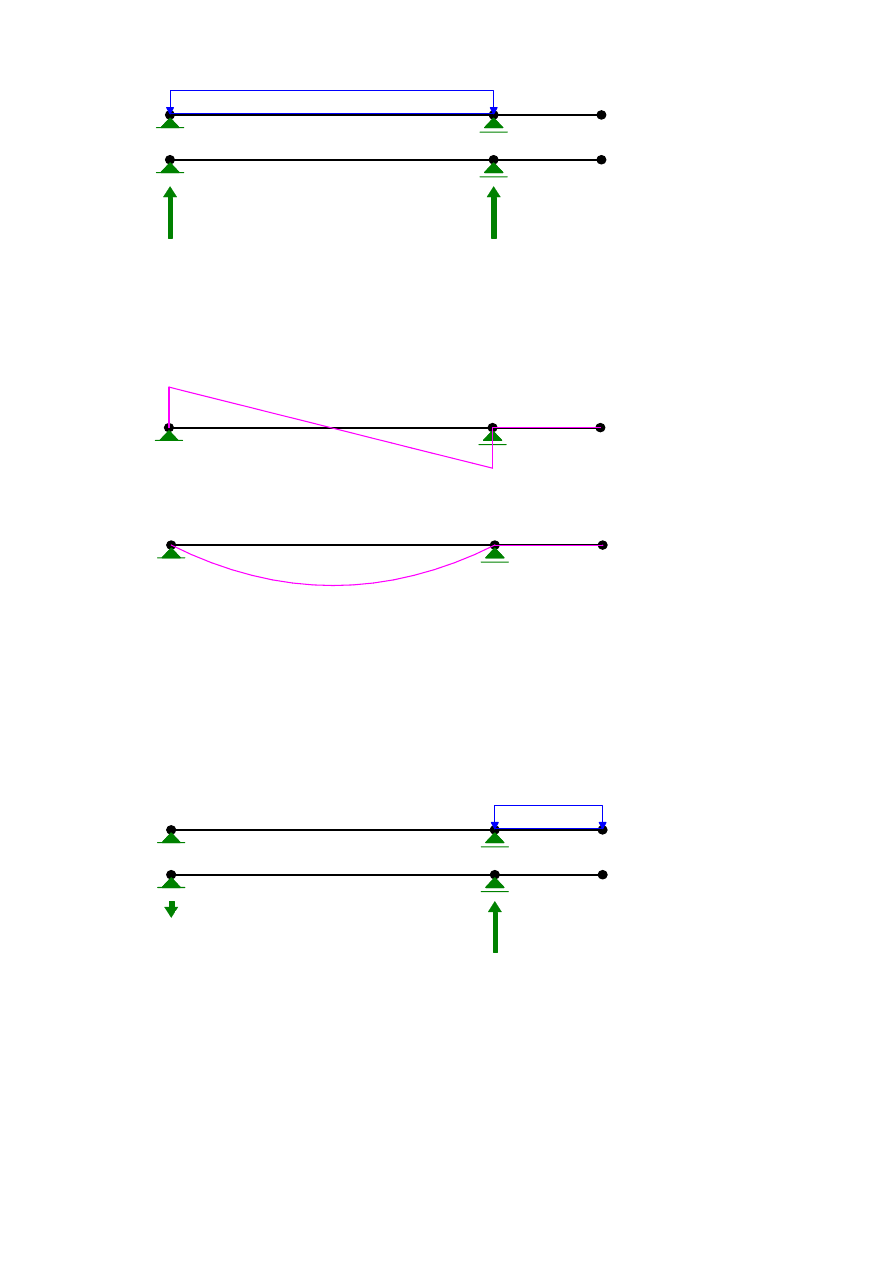
4.2 Obciążenie zmienne p na ropiętości L

1

~ Wyznaczenie reakcji od obciążenia zmiennego p

R

A

= R

B

= 0,5 p L

1

=

4

kN

~ Wykres sił tnących

T [kN]

~ Wykres momentów zginających

M [kNm]

~ Maksymalne momenty od obciążenia zmiennego p

* przęsłowy

M

max

= p L

1

2

/ 8 =

81

kNm

* podporowy

M

min

=

0

kNm

4.3 Obciążenie zmienne p na rozpietosci L

2

~ Wyznaczenie reakcji od obciążenia zmiennego p

Σ

M

B

= 0

0,5 p * L

2

2

- R

A

* L

1

= 0

R

A

= 0,5 p * L

2

2

/ L

1

R

A

=

4

kN

Σ

Y = 0

R

A

+ p * L

2

- R

B

= 0

R

B

=

28

kN

1

2

8,000

8,000

1

2

3

R

A

R

B

1

2

36,000

-36,000

36,000

-36,000

1

2

81,000

1

2

3

4,000

1

2

8,000

8,000

R

A

R

B

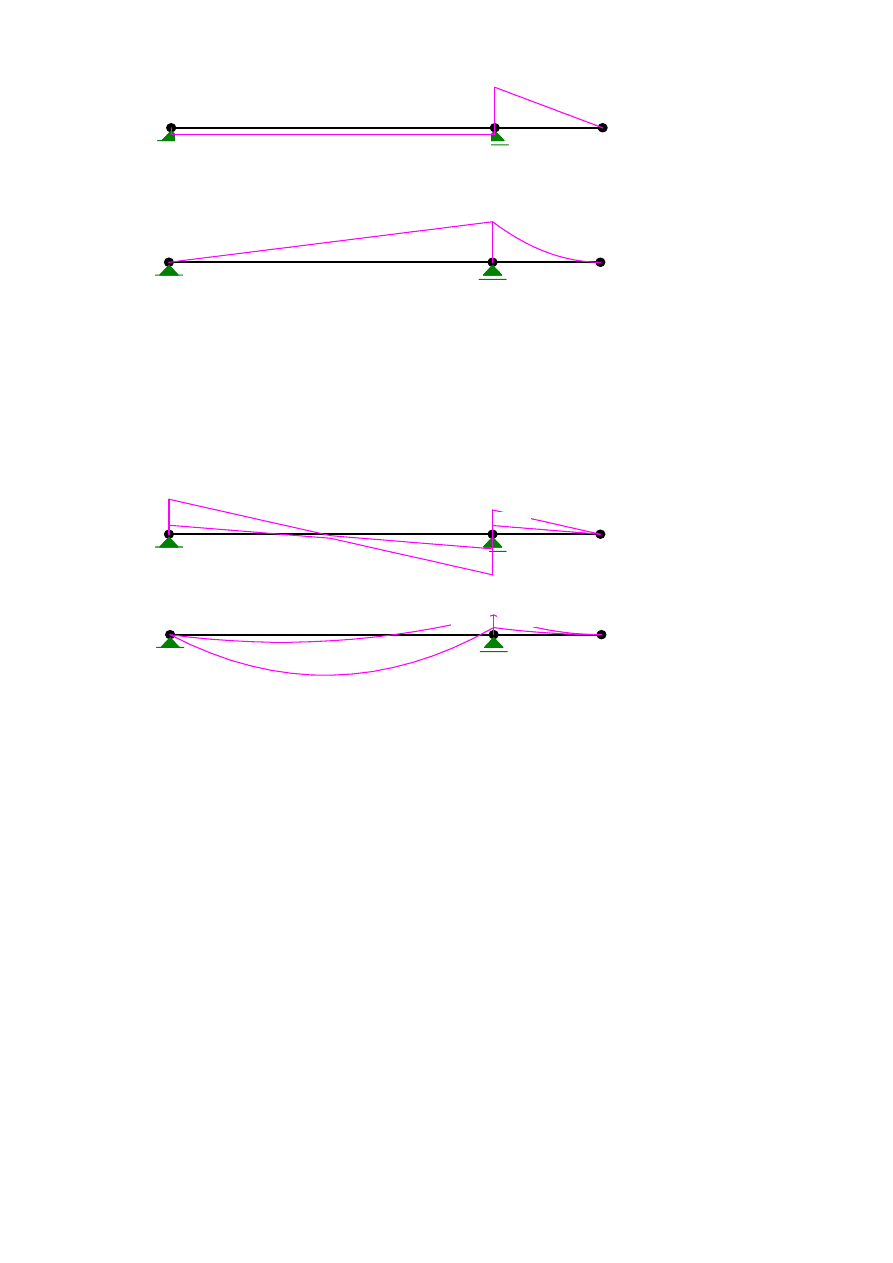
~ Wykres sił tnących

T [kN]

~ Wykres momentów zginających

M [kNm]

~ Maksymalne momenty od obciążenia zmiennego p

* przęsłowy

M

max

=

-

kNm

* podporowy M

min

= -R

A

* L

1

=

-36

kNm

4.4 Obwiednia sił tnących i momentów zginających

T [KN]

M [kNm]

~ Maksymalny moment przesłowy od obciążenia stałego i zmiennego

M

max

= M

max

(g, x= 4) + M

max

(p, x=4,5) =

117

kNm

Maksymalny moment przęsłowy od obciążeń stałego i zmiennego występuje w połowie rozpiętości L

1

i wynosi 116,44 kNm (wartość odczytana z programu). Do obliczeń można przyjąć warość 117 kN
ponieważ obliczeniowo znajdujemy się po strone bezpiecznej (moment obliczony jest większy
od rzeczywistego).

~ Maksymalny moment podporowy od obciążeia stałego i zmiennego

M

min

=

-56,25

kNm

1

2

-4,000

-4,000

-4,000

-4,000

24,000

24,000

1

2

-36,000

-36,000 -36,000

-36,000

1

2

54,000

14,000

-22,500

-62,500

37,500
13,500

1

2

-20,250

-56,250

-20,250

-56,250

5.0 Wymiarowanie przekroju z uwagi na zginanie

5.1 Określenie wysokości użytecznej przekroju

~ Otulenie prętów zbrojenia

c

min

=

2

cm

minimalna grubość otulenia dla klasy ekspozycji XC2

∆

c =

0,5

cm

odchyłka otuliny

c

nom

= c

min

+

∆

c =

2,5

cm

całkowita grubość otuliny

~ Wysokość użyteczna przekroju

d = h - c -

φ

strz

- 0,5

φ

gł

=

56,3

cm

pręty ułożone w jednym rzędzie

5.1 Maksymalny moment przęsłowy

~ Minimalne pole przekroju zbrojenia głównego

0,26 b

d

d f

ctm

/f

yk

=

1,288

cm

2

0,0013 b

d

d =

1,464

cm

2

A

s1,min

=

1,464

cm

2

~ Określenie rodzaju przekroju

M

f

= h

g

b

g

α

cc

f

cd

(d – 0,5h

g

) = 431,053 kNm

moment płytowy

α

cc

= 1

M

f

= 431,053

>

M

max

=

117

kNm

przekrój pozornie teowy

0,079

[-]

0,083

<

ξ

eff,lim

=

0,5

[-]

przekrój pojedynczo zbrojony

5,161

cm

2

> A

s1,min

=

1,464

cm

2

ilość potrzebnych prętów

φ

12:

n = A

s1

/ A

φ

12

=

4,564

szt

przyjęto

5

szt

A

s1,prov

= n A

φ

12

=

5,655

cm

2

pole zastosowanego zbrojenia

ρ

L

= A

s1,prov

/A

c

* 100%=

0,42

%

stopień zbrojenia

=

⋅

⋅

=

cd

g

sd

eff

f

d

b

M

2

µ

=

⋅

−

−

=

eff

eff

µ

ξ

2

1

1

=

⋅

⋅

⋅

=

yd

cd

g

eff

s

f

f

b

d

A

ξ

1











⋅

⋅

⋅

=

d

b

d

b

f

f

A

d

d

yk

ctm

s

0013

,

0

26

,

0

max

min

,

1

5.2 Maksymalny moment podporowy

~ Minimalne pole przekroju zbrojenia głównego

0,26 b

g

d f

ctm

/f

yk

=

3,175

cm

2

0,0013 b

g

d =

2,562

cm

2

A

s1,min

=

3,175

cm

2

~ Określenie rodzaju przekroju

M

f

= h

d

b

d

α

cc

f

cd

(d – 0,5h

g

) = 136,458 kNm

moment płytowy

α

cc

= 1

M

f

= 136,458

>

M

max

=

56,25

kNm

przekrój pozornie teowy

0,067

[-]

0,069

<

ξ

eff,lim

=

0,5

[-]

przekrój pojedynczo zbrojony

2,464

cm

2

< A

s1,min

=

3,175

cm

2

ilość potrzebnych prętów

φ

12:

n = A

s1,min

/ A

φ

12

=

2,807

szt

przyjęto

3

szt

A

s1,prov

= n A

φ

12

=

3,393

cm

2

pole zastosowanego zbrojenia

ρ

L

= A

s1,prov

/A

c

* 100%=

0,25

%

stopień zbrojenia

6.0 Wymiarowanie przekroju z uwagi na ścinanie

Przyjęto zbrojenie strzemionami dwucietymi

φ

6 ze stali klasy A-II

A

sw

= 2A

φ

6

=

0,565

cm

2

6.1 Podpora A z prawej strony

k = 1,6 - d =

1,037

>1

ρ

L

=

0,0042

< 0,01

przyjęto, że wszystkie pręty z przęsła są zakotwione

na długość lbd + d poza rozpatrywany przekrój

σ

cp

=

0

MPa

naprężenie ściskające wywołane działaniem siły podłużnej

=

⋅

⋅

=

cd

g

sd

eff

f

d

b

M

2

µ

=

⋅

−

−

=

eff

eff

µ

ξ

2

1

1

=

⋅

⋅

⋅

=

yd

cd

g

eff

s

f

f

b

d

A

ξ

1











⋅

⋅

⋅

=

d

b

d

b

f

f

A

g

g

yk

ctm

s

0013

,

0

26

,

0

max

min

,

1

d

b

f

k

V

s

cp

L

ctd

Rd

⋅

+

+

⋅

⋅

=

]

15

,

0

)

40

2

,

1

(

35

,

0

[

1

σ

ρ

V

Rd1

=

41,917

kN

V

Sd

d

=

46,975

kN

siła tnąca w odległości d od podpory

V

Sd

d

> V

Rd1

- odcinek II rodzaju

ν

= 0,6 (1 - f

ck

/250) =

0,552

[-]

z = 0,9 d =

0,5067

m

ramię sił wewnętrznych w przekroju

ctg

θ

=

1

[-]

V

Rd2

= 278,999 [kN]

V

Sd

d

< V

Rd2

- warunek SGN jest spełniony

~ wyznaczenie rozstawu strzemion

s

1

=

18,91

cm

przyjęto strzemiona w rozstawie s

1

=

18

cm

~ określenie długosci odcinka II rodzaju

0,967

m

odległośc liczona od osi podpory

~ stopień zbrojenia strzemionami

0,0010

[-]

0,0021

[-]

>

ρ

w,min

6.2 Podpora B z lewej strony

k = 1,6 - d =

1,037

>1

ρ

L

=

0,0025

< 0,01

przyjęto, że wszystkie pręty z podpory są zakotwione

na długość lbd + d poza rozpatrywany przekrój

σ

cp

=

0

MPa

naprężenie ściskające wywołane działaniem siły podłużnej

V

Rd1

=

39,863

kN

V

Sd

d

=

55,475

kN

siła tnąca w odległości d od podpory

V

Sd

d

> V

Rd1

- odcinek II rodzaju

θ

θ

ν

2

2

ctg

1

ctg

+

⋅

⋅

⋅

⋅

=

z

b

f

V

s

cd

Rd

θ

θ

ctg

ctg

1

1

1

1

1

1

3

⋅

⋅

⋅

=

⇒

⋅

⋅

⋅

=

=

z

V

f

A

s

z

s

f

A

V

V

d

sd

ywd

sw

ywd

sw

d

sd

Rd

=

+

−

=

p

g

V

V

c

Rd

Sd

1

=

⋅

=

s

sw

w

b

s

A

1

1

ρ

d

b

f

k

V

s

cp

L

ctd

Rd

⋅

+

+

⋅

⋅

=

]

15

,

0

)

40

2

,

1

(

35

,

0

[

1

σ

ρ

=

=

yk

ck

w

f

f

08

,

0

min

,

ρ

ν

= 0,6 (1 - f

ck

/250) =

0,552

[-]

z = 0,9 d =

0,5067

m

ramię sił wewnętrznych w przekroju

ctg

θ

=

1

[-]

V

Rd2

= 278,999 [kN]

V

Sd

d

< V

Rd2

- warunek SGN jest spełniony

~ wyznaczenie rozstawu strzemion

s

1

=

18,34

cm

przyjęto strzemiona w rozstawie s

1

=

18

cm

~ określenie długosci odcinka II rodzaju

1,81

m

odległośc liczona od osi podpory

~ stopień zbrojenia strzemionami

0,0010

[-]

0,0021

[-]

>

ρ

w,min

6.3 Podpora B z prawej strony

k = 1,6 - d =

1,037

>1

ρ

L

=

0,0025

< 0,01

przyjęto, że wszystkie pręty z podpory są zakotwione

na długość lbd + d poza rozpatrywany przekrój

σ

cp

=

0

MPa

naprężenie ściskające wywołane działaniem siły podłużnej

V

Rd1

=

39,863

kN

V

Sd

d

=

30,475

kN

siła tnąca w odległości d od podpory

V

Sd

d

< V

Rd1

- odcinek I rodzaju (strzemiona konstrukcyjne)

~ Rozstaw strzemion na odcinakch I rodzaju

s

max

= 0,75d =

42,225

cm

>

40

cm

θ

θ

ν

2

2

ctg

1

ctg

+

⋅

⋅

⋅

⋅

=

z

b

f

V

s

cd

Rd

θ

θ

ctg

ctg

1

1

1

1

1

1

3

⋅

⋅

⋅

=

⇒

⋅

⋅

⋅

=

=

z

V

f

A

s

z

s

f

A

V

V

d

sd

ywd

sw

ywd

sw

d

sd

Rd

=

+

−

=

p

g

V

V

c

Rd

Sd

1

=

⋅

=

s

sw

w

b

s

A

1

1

ρ

=

=

yk

ck

w

f

f

08

,

0

min

,

ρ

d

b

f

k

V

s

cp

L

ctd

Rd

⋅

+

+

⋅

⋅

=

]

15

,

0

)

40

2

,

1

(

35

,

0

[

1

σ

ρ

7.0 Nosność zbrojenia głównego przy ścinaniu

sprawdzenia poniższego warunku dokonuje się na odcinkach II rodzaju

gdy nie stosuje się prętów odgiętych wzór upraszcza się do postaci

7.1 Podpora A z prawej strony

M

Sd

d

=

28,372

kNm

moment odpowiadajacy max sile tnacej w odległości d od podpory

z = 0,9d =

0,5067

m

ramię sił wewnętrznych

V

Sd

d

=

46,975

kN

A

s1

=

5,655

cm

2

pole zbrojenia głównego

f

yd

=

420

MPa

granica plastyczności stali zbrojenia głównego

∆

F

td

=

23,488

kN

F

td

=

79,481

<

A

s1

f

yd

= 237,504 kN

nośność zbrojenia głównego jst wystarczająca

7.2 Podpora B z lewej strony

M

Sd

d

=

23,101

kNm

moment odpowiadajacy max sile tnacej w odległości d od podpory

z = 0,9d =

0,5067

m

ramię sił wewnętrznych

V

Sd

d

=

55,475

kN

A

s1

=

3,393

cm

2

pole zbrojenia głównego

f

yd

=

420

MPa

granica plastyczności stali zbrojenia głównego

∆

F

td

=

27,738

kN

F

td

=

73,329

<

A

s1

f

yd

= 142,503 kN

nośność zbrojenia głównego jst wystarczająca

yd

s

td

Sd

td

f

A

F

z

M

F

⋅

≤

+

=

1

∆













−

=

α

θ

∆

ctg

ctg

5

,

0

3

32

Rd

Rd

Sd

td

V

V

V

F

θ

∆

ctg

5

,

0

⋅

=

Sd

td

V

F