3. Belka stropowa
3.1 Zestawienie obciążeń na 1mb belki.
3.1.1 Obciążenia stałe.
•

Z płyty stropowej:

•

Ciężar własny belki np. IPE300:

Razem obciążenie stałe:

•

Do pierwszej iteracji obliczeń można wstępnie przyjąć belkę o

wysokości dobranej z warunku

20

/

20

/

b

L

h

b























6

;

5

15

,

1

,

1

L

L

g

g

s

k

k

m

kN

m

/

42

,

0



m

g

g

k

k





1

3.1.2 Obciążenia zmienne.
•

Obciążenie użytkowe ze stropu:

3.2 Kombinatoryka (wg PN-EN 1990)
3.2.1 Kombinacje SGN
Jako miarodajną należy wybrać kombinację mniej korzystną z

wyrażeń (6.10a) i (6.10b).



















6

;

5

25

,

1

L

L

p

q

k













1

1

,

,

0

,

1

,

1

,

0

1

,

,

,

"

"

"

"

j

i

i

K

i

i

Q

K

Q

j

k

j

G

Q

Q

G























1

1

,

,

0

,

1

,

1

,

,

,

"

"

"

"

j

i

i

K

i

i

Q

K

Q

j

k

j

G

j

Q

Q

G











Kombinacje SGN

Jako miarodajną wybrać wartość większą
3.2.2 Kombinacje SGU

q

g

p

q

g

p

k

k





















5

,

1

35

,

1

85

,

0

7

,

0

5

,

1

35

,

1

2

1





2

1

;

max

p

p

p

d



Kombinacja charakterystyczna dla SGU (dla danych z projektu):

3.3 Obliczenia statyczne.
3.3.1 Schemat statyczny.
Schematem statycznym jest belka swobodnie podparta z obciążeniem

ciągłym.

Długość obliczeniowa belki:

gdy belka jest dwustronnie oparta na ścianie

gdy belka jest jednostronnie oparta na ścianie

gdzie: L

s

– rozpiętość mierzona w świetle muru

Uwaga: W projekcie należy przyjąć:

q

g

p

k

k





s

o

L

L





05

,

1

s

o

L

L





025

,

1

b

L

o



3.3.2 Wyznaczenie sił przekrojowych.

Wyznaczenie maksymalnych sił przekrojowych (M, V) dla kombinacji

SGN:

2

8

2

b

p

V

b

p

M

d

Ed

d

Ed









3.3.2 Wyznaczenie ugięcia belki.
Wyznaczenie maksymalnego ugięcia dla kombinacji charakterystycznej

(SGU):

Wymiarowanie przekroju (wg PN-EN 1993-1-1):
3.4 Sprawdzenie SGU.
Dla belek drugorzędnych (tablica w punkcie NA 22 wg załącznika

krajowego do normy PN-EN 1993-1-1):

y

k

I

E

b

p

w







4

max

384

5

250

250

max

b

l

w





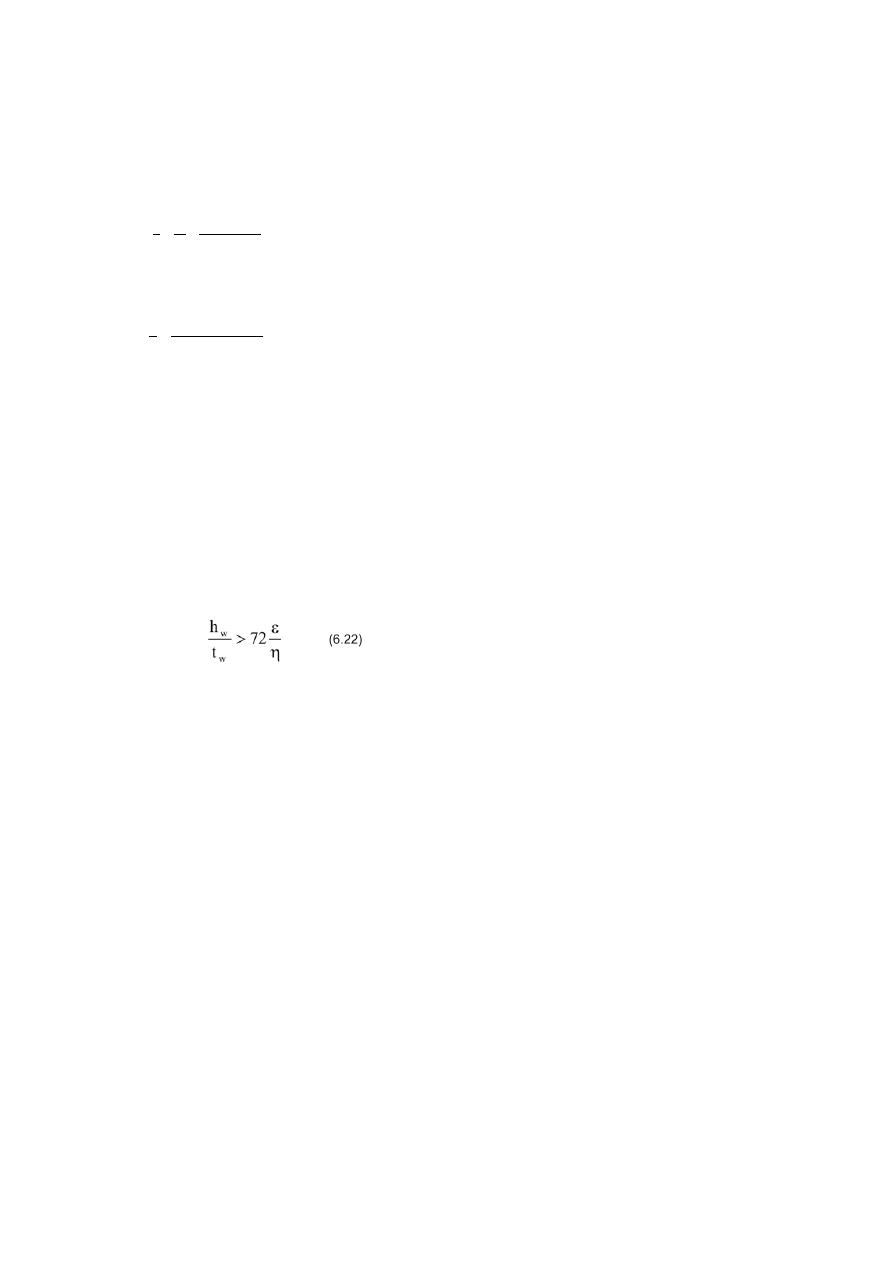
3.5 Sprawdzenie SGN.
3.5.1. Określenie klasy przekroju.
• Klasa przekroju ze względu na środnik (część zginana):

porównujemy z Tablicą 5.2 (arkusz 1 z 3)

• Klasa przekroju ze względu na pas (część ściskana):

porównujemy z Tablicą 5.2 (arkusz 2 z 3)

Przekrój jest klasyfikowany według najwyższej (najmniej korzystnej)

klasy jego części ściskanych.

w

f

w

t

r

t

h

t

d

t

c

)

(

2









f

w

t

r

t

b

t

c

)

2

(

5

.

0









3.5.2. Sprawdzenie stateczności środnika przy ścinaniu.
W przypadku nieużebrowanych środników należy uwzględnić warunek

statyczności jeżeli:

h

w

- wysokość środnika w świetle półek;

dla stali

dla stali

Uwaga:
Jeżeli warunek nie jest spełniony to środnik nie jest narażony na utratę

stateczności, w przeciwnym wypadku należy sprawdzić warunek

nośności wg rozdziału 5 normy PN-EN 1993-1-5.

f

w

t

h

h







2

2

,

1





]

/

[

460

2

mm

N

f

y



0

,

1





]

/

[

460

2

mm

N

f

y



3.5.3. Sprawdzenie nośności na zginanie (norma pkt. 6.2.5)

W

pl

– wskaźnik oporu plastycznego

W

el,min

– najmniejszy sprężysty wskaźnik wytrzymałości

W

eff,min

– najmniejszy wskaźnik wytrzym. przekroju współpracującego

W

pl

i W

el

można znaleźć w tablicach (www.constructalia.com)

3.5.4. Sprawdzenie nośności na ścinanie (norma pkt. 6.2.6)

V

c,Rd

– obliczeniowa nośność przekroju przy ścinaniu.

• Przy projektowaniu plastycznym:

A

v

– pole przekroju czynnego przy ścinaniu wg. 6.2.6(3a):

Dla przekrojów dwuteowych walcowanych, ścinanych prostopadle
do osi y-y:





w

w

f

w

f

v

t

h

t

r

t

t

b

A

A























2

2

3.5.5. Sprawdzenie nośności na zginanie ze ścinaniem (norma pkt.

6.2.8).

Jeżeli z punktu 3.5.2 wyjdzie, że środnik nie jest narażony na utratę

stateczności oraz spełnione jest:

to wpływ ścinania przy zginaniu można pominąć.

5

,

0

,



Rd

pl

Ed

V

V

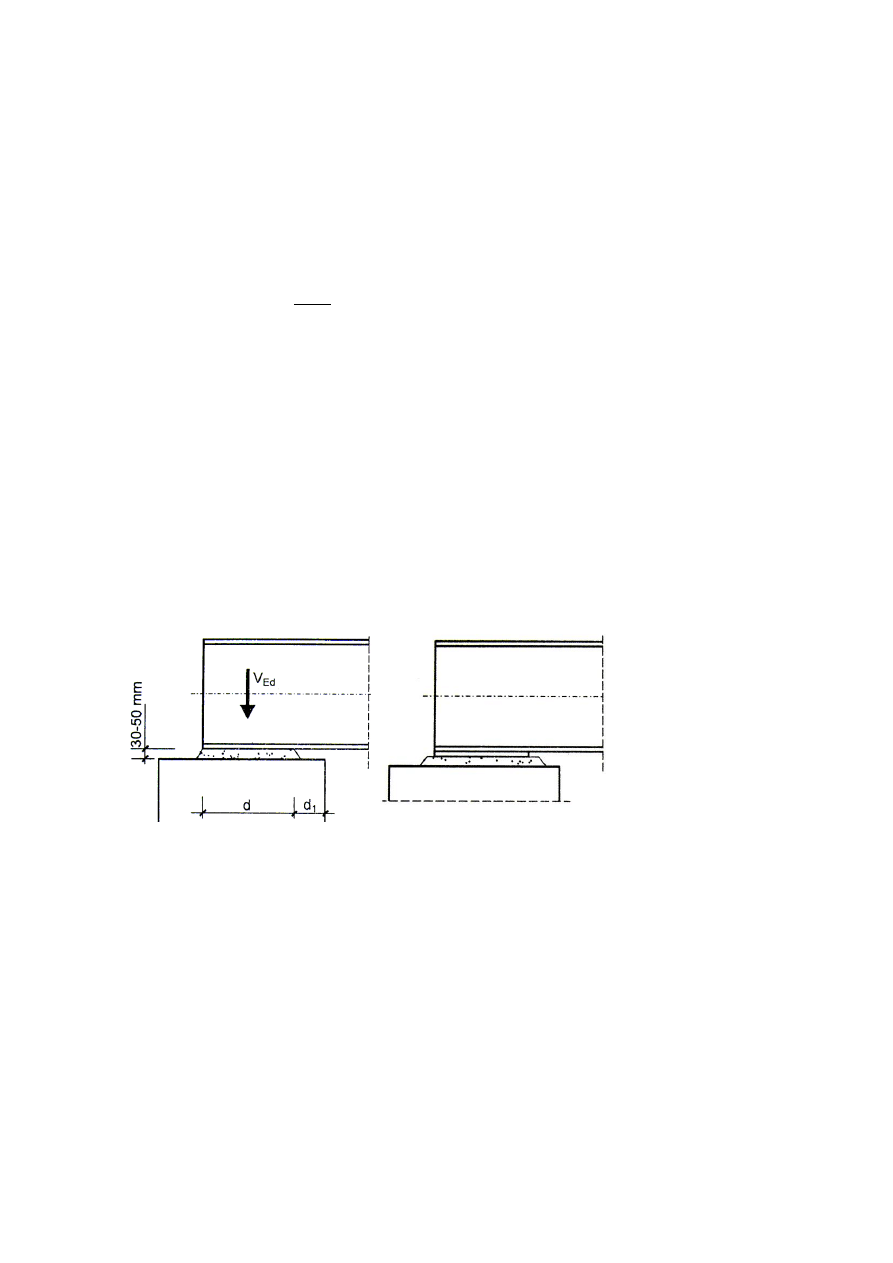
3.5.7 Sprawdzenie nośności oparcia belki na ścianie.

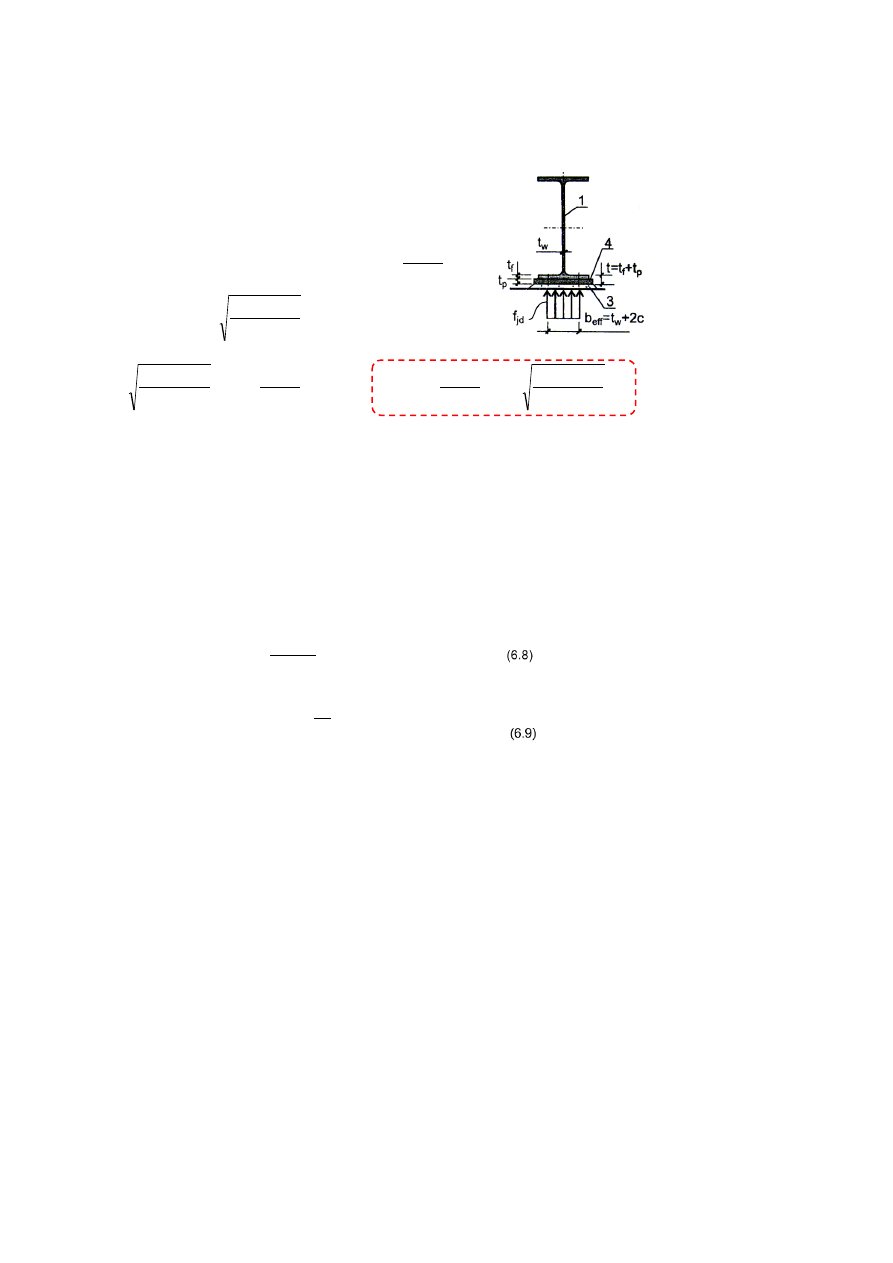
Szczegół oparcia belki na ścianie:

Bez podkładki:

Z podkładką:

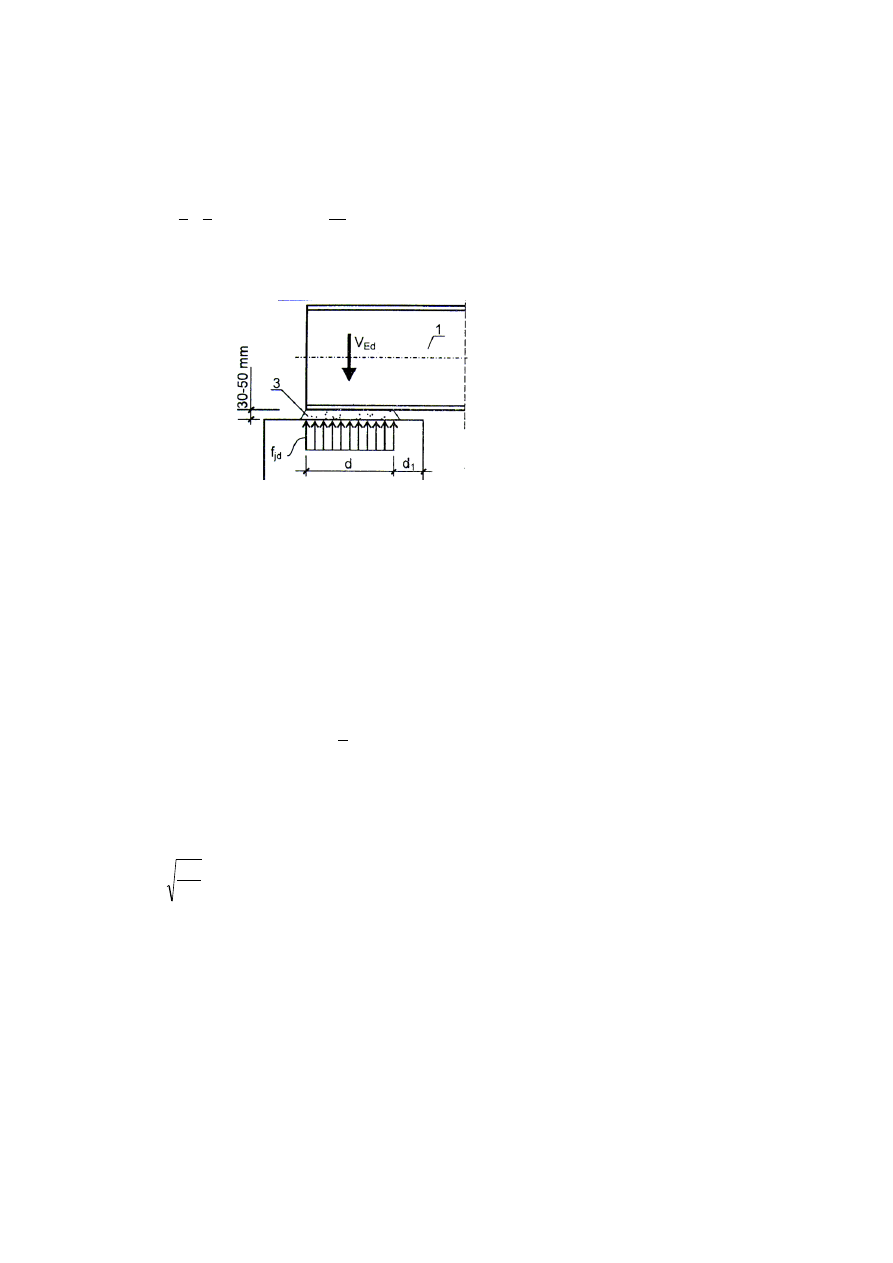
Algorytm postępowania

1) Wyznaczenie obliczeniowej wartości reakcji podporowej V

Ed

2) Przyjęcie długości oparcia belki d:

3) Przyjęcie odsunięcia belki od lica ściany d

1

w celu zapobiegnięciu

odłupywania się naroża ściany:

 

belki

wysokośy

:

gdzie

,

30

150

oraz

2

3











h

mm

h

d

h

h

d

mm

d

50

30

1





4) Wyznaczenie nośności ściany na obciążenie dociskiem miejscowym.
F

C,Rd

– obliczeniowa nośność przy docisku króćca teowego do betonu:

f

jd

– obliczeniowa wytrzymałość na docisk:

Przy założeniu

można wstępnie przyjąć



=1,5 wtedy:

Gdyby d

1

=0 to należałoby przyjąć



=1,0.

Uwaga:
Po obliczeniu nośności należy sprawdzić poprawność przyjęcia



:

A

c0

– powierzchnia docisku króćca teowego

A

c1

– powierzchnia rozdziału

eff

eff

jd

eff

jd

Rd

C

l

b

f

A

f

F











,

cd

j

jd

f

f











cd

cd

jd

f

f

f









3

2

5

.

1

mm

d

50

30

1





:

gdzie

,

0

1

c

c

A

A





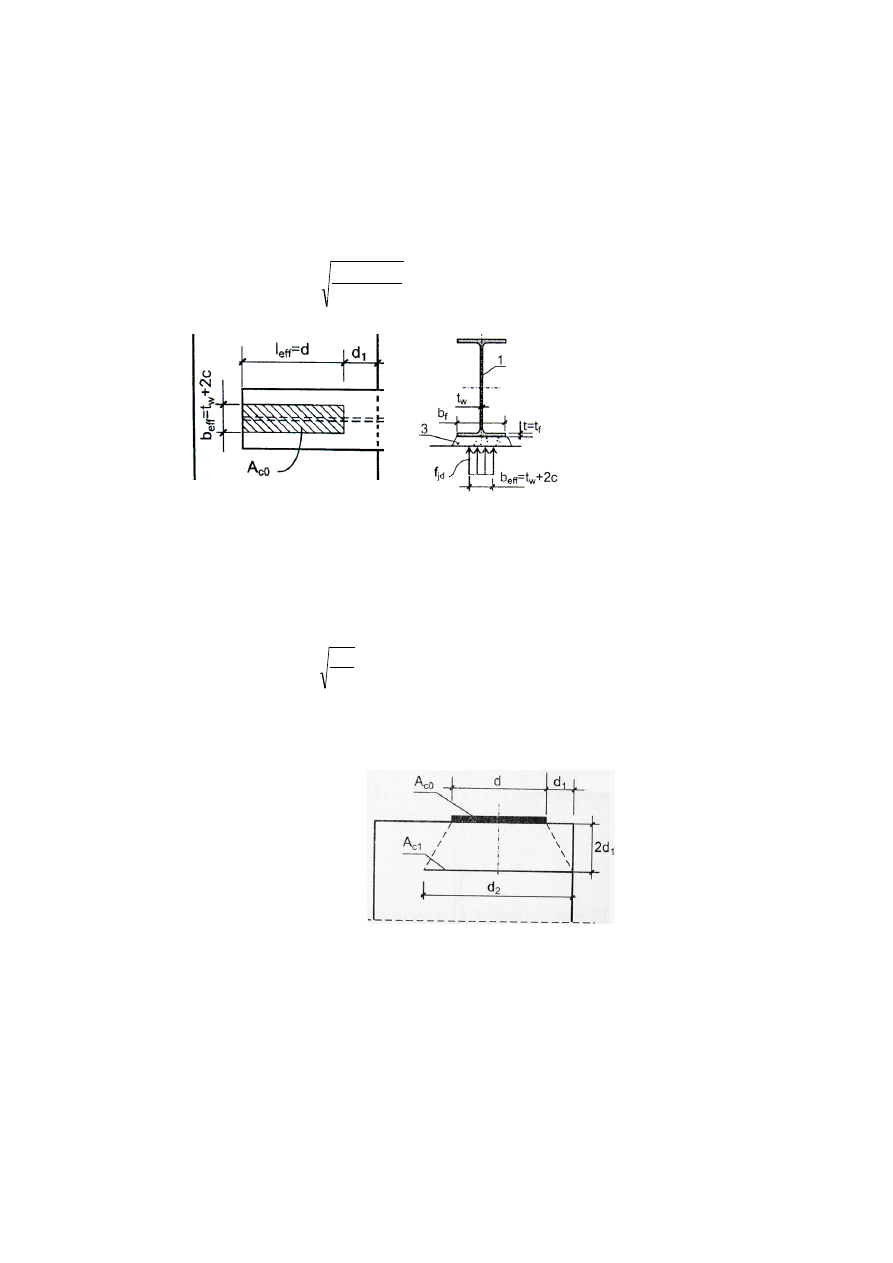
5) Wyznaczenie powierzchni docisku belki do ściany:

gdzie:

c – maksymalny wysięg strefy docisku:

c

t

b

w

eff







2

d

l

eff



0

3

M

jd

y

f

f

t

c









6) Sprawdzenie warunku nośności ściany na obciążenie dociskiem

miejscowym:

Jeżeli warunek spełniony to należy jeszcze sprawdzić poprawność

przyjętego założenia



≥1,5:

A

c0

– powierzchnia docisku króćca teowego; A

c0

= A

eff

= b

eff

l

eff

A

c1

– powierzchnia rozdziału (maksymalna powierzchnia

współpracująca przy przenoszeniu obciążenia);

Uwaga: Jeżeli



<1,5 to należy

Przyjąć wyliczoną



i ponowić

obliczenia nośności.

Rd

C

Ed

F

V

,



:

gdzie

,

0

1

c

c

A

A











1

1

1

2

2

d

b

d

l

A

eff

eff

c







Jeżeli

to można wyznaczyć grubość dodatkowej

podkładki z blachy korzystając ze znanych zależności:

Po przyjęciu grubości podkładki t

p

należy policzyć rzeczywisty wysięg

strefy docisku c dla t = t

f

+ t

p

oraz sprawdzić formalnie warunek

nośności

Rd

C

Ed

F

V

,



Rd

c

Ed

F

V

,



eff

eff

jd

Ed

l

b

f

V













































w

jd

Ed

w

jd

Ed

t

d

f

V

c

d

c

t

f

V

5

,

0

2

f

y

M

jd

w

jd

Ed

p

w

jd

Ed

M

jd

y

t

f

f

t

d

f

V

t

t

d

f

V

f

f

t



























































0

0

3

5

,

0

5

,

0

3





c

t

b

w

eff







2

d

l

eff



0

3

M

jd

y

f

f

t

c









p

f

t

t

t





Rd

C

Ed

F

V

,



3.5.8 Sprawdzenie nośności środnika pod działaniem obciążenia skupionego (wg PN-EN-1993-1-5,
punktu 6).

3) Obliczenie współczynników m

1

i m

2

(wg punktu 6.5 normy)

f

yf

– granica plastyczności pasa;

f

yw

– granica plastyczności środnika;

b

f

, t

f

– szerokość, grubość pasa;

h

w

, t

w

– wysokość, grubość środnika.

Uwaga:
Wstępnie można przyjąć, że

i obliczyć wartość m

2

.

w

yw

f

yf

t

f

b

f

m







1









































5

,

0

,

,

0

5

,

0

,

02

,

0

2

2

2

F

F

f

w

gdy

m

gdy

t

h

m





5

,

0





F



4) Obliczenie szerokości efektywnej l

y

(wg punktu 6.5 normy)

W przypadku obciążenia „typu c”:

w którym parametr niestateczności przy obciążeniu „typu c”:

2

2

1

1

2

m

t

l

m

t

l

l

f

e

f

e

y























6

6

2













 





w

s

F

h

c

s

k

c

s

h

f

t

E

k

l

s

w

yw

w

F

e















2

2





:

którym

w

,

,

min

2

1

y

y

y

l

l

l



:

gdzie

,

2

1

2

m

m

t

l

l

f

e

y







5) Obliczenie smukłości

Uwaga:
Jeżeli smukłość , to należy przyjąć m

2

=0 i powtórzyć obliczenia.

:

gdzie

,

cr

yw

w

y

F

F

f

t

l







w

w

F

cr

h

t

E

k

F

3

9

,

0



5

,

0





F



6) Obliczenie współczynnika redukcyjnego χ

F

7) Obliczenie efektywnego wymiaru środnika przy obciążeniu

skupionym L

eff

8) Obliczenie nośność środnika ze względu na niestateczność pod siłą

skupioną.

9) Sprawdzenie warunku nośności.

F

Ed

– obliczeniowa siła skupiona; F

Ed

= V

Ed

0

,

1

5

,

0







F

F





y

F

eff

l

L







0

,

1

:

gdzie

,

1

1









M

M

w

eff

yw

Rd

t

L

f

F





:

gdzie

,

0

,

1

2





Rd

Ed

F

F

