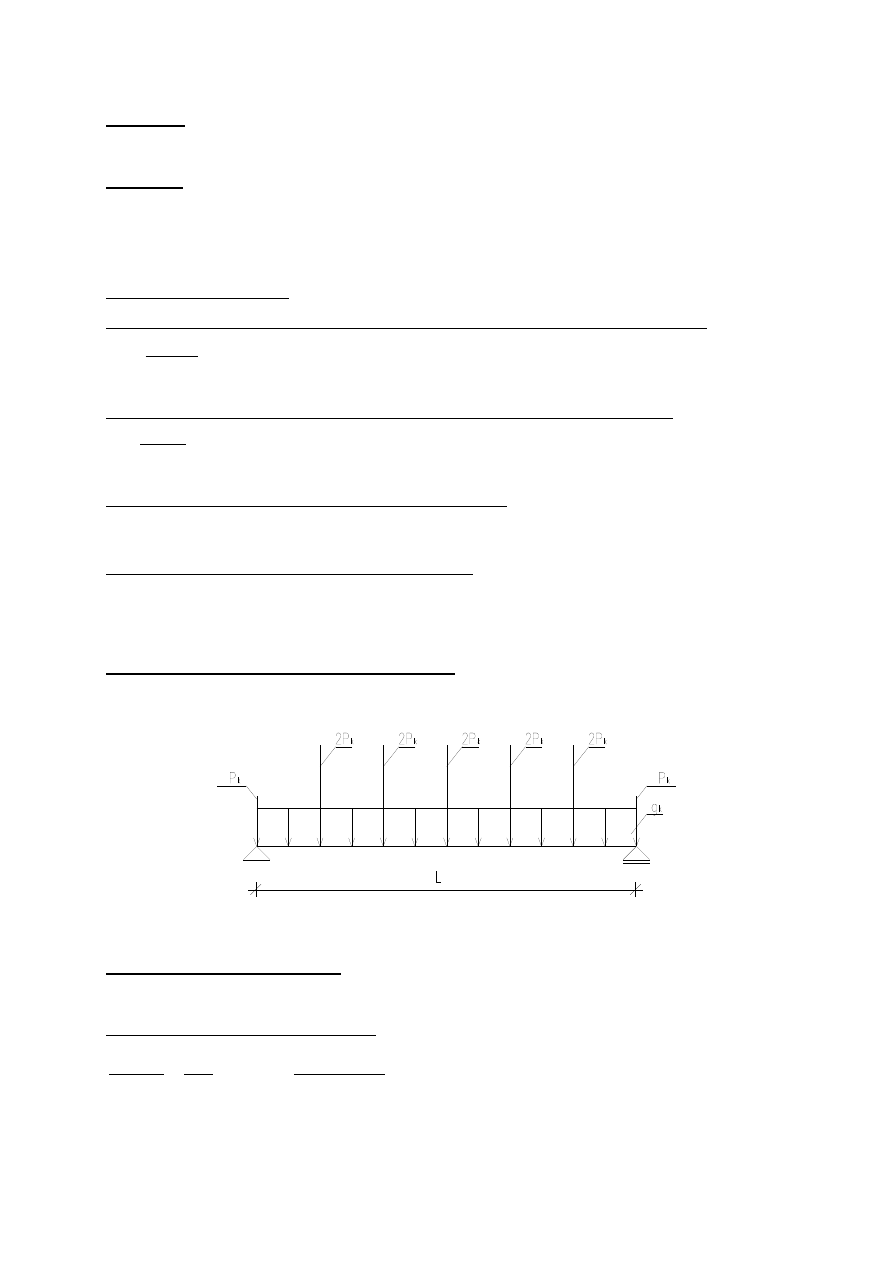
1

3. Podciąg

UWAGA:

Obciążenie belek stropowych zostało zwiększone współczynnikiem 1,15 ze względu na
większą reakcję przekazywaną na podporę przedskrajną. Reakcje przekazywane z belek
stropowych na podciąg należy obliczyć bez uwzględniania współczynnika 1,15.

3.1.Obciążenia podciągu

- charakterystyczne obciążenie przekazywane w postaci reakcji z belek stropowych

]

kN

[

2

b

k

k

L

p

P





- obliczeniowe obciążenie przekazywane w postaci reakcji z belek stropowych

]

kN

[

2

b

o

L

p

P





- charakterystyczna wartość ciężaru własnego podciągu

]

N/m

[

5

,

8

)

10

70

(









L

g

k

- L należy podstawić w [m]

- obliczeniowa wartość ciężaru własnego podciągu

sup

,

G

k

o

g

g







;

gdzie:

35

,

1

sup

,



G



3.1.Schemat statyczny podciągu z obciążeniami

3.2.Wstępne przyjęcie przekroju

-wskaźnik wytrzymałości plastycznej

y

M

Ed

y

pl

M

y

y

pl

Ed

f

M

W

f

W

M

0

max,

,

0

,

max,













2

-moment bezwładności

L

M

n

I

Ek

gr

y









max,

051

,

0

,

gdzie: M

max,Ek

[kN/m]; L [m];

n

gr

=350

-wysokość blachownicy

L

h

L

10

1

12

1





y

pl

y

y

pl

y

W

I

h

W

I

h

,

min

,

min

2

2









UWAGA:

Całkowitą wysokość belki zaleca się zaokrąglać do wielokrotności 50mm lub 100mm, co
umożliwia identyfikację elementów podczas scalania konstrukcji a także ich inwentaryzację w
okresie eksploatacji.

-wysokość środnika ze względu na kryterium minimalnego ciężaru

w

y

el

w

t

W

h

,





; gdzie α=1,1 ; 1,2 dla belki o przekroju odpowiednio stałym i zmiennym

-pole próbne przekroju pasa blachownicy

6

,

w

y

pl

f

A

d

W

A





gdzie: A

w

– pole przekroju środnika (grubość środnika t

w

> 7mm)

d – odległość między środkami ciężkości pasów

-szerokość pasa blachownicy

4

5

w

f

w

h

b

h





UWAGA:

Należy tak dobrać wymiary półki, aby była klasy 1,2 lub 3 oraz nie wystąpił efekt szerokiego
pasa

-grubość pasa blachownicy

f

f

f

b

A

t



3

3.3.Wymiary i charakterystyki geometryczne przekroju

- wysokość:

h [mm]

- wysokość środnika:

h

w

[mm]

- grubość środnika:

t

w

[mm]

- szerokość półki:

b

f

[mm]

- grubość półki:

t

f

[mm]

- moment bezwładności:

I

y

[mm

4

]



 



12

12

2

3

3

w

w

f

f

w

f

y

h

t

b

t

h

b

I















- sprężysty wskaźnik wytrzymałości: W

y

[mm

3

]

h

I

W

y

y





2

UWAGA:

Po przyjęciu przekroju można sprawdzić ugięcia wg wzoru:

350

48

5

,

5

max

2

max,

L

w

I

E

L

M

w

y

Ek













- ugięcie graniczne dla belek stropowych głównych wg.

załącznika krajowego do PN-EN-1993-1-1.

3.4.Określenie klasy przekroju

- przyjęcie spoin łączących środnik z pasem

min

max

7

,

0

2

,

0

t

a

t







oraz

mm

3



a

- Klasa przekroju ze względu na środnik

w

w

t

a

h

t

d

t

c

2

2









- Klasa przekroju ze względu na pas





f

w

f

t

a

t

b

t

c

2

5

.

0









UWAGA:

Warunki graniczne smukłości dla poszczególnych części elementów ściskanych podano w

p.2.3 oraz Tablicy 5.2 – PN-EN 1993-1-1

y

f

235





4

3.5.Sprawdzenie występowania efektu szerokiego pasa

Obliczenia wg PN-EN-1993-1-5 p.3.

Jeżeli spełniony jest warunek:

50

0

e

L

b



to efekty szerokiego pasa nie występuje

gdzie: b

0

– szerokość wystającej(wspornikowej) części pasa:





w

f

t

b

b







5

,

0

0

,

lub połowa szerokości części przęsłowej(dwustronnie podpartej):

w

h

b





5

,

0

0

L

e

– odległość między punktami zerowych momentów zginających:

L

L

e



3.7.Sprawdzenie nośności na zginanie

Obliczeniowa nośność przekroju przy jednokierunkowym zginaniu, względem głównej osi

bezwładności wynosi:

0

,

,

M

y

pl

Rd

pl

Rd

c

f

W

M

M









- przekroje klasy 1. i 2.

(6.13)

gdzie

pl

W

- wskaźnik oporu plastycznego

0

min

,

,

,

M

y

el

Rd

el

Rd

c

f

W

M

M









- przekroje klasy 3.

(6.14)

gdzie

min

,

el

W

- najmniejszy sprężysty wskaźnik wytrzymałości

0

min

,

,

M

y

eff

Rd

c

f

W

M







- przekroje klasy 4.

(6.15)

gdzie

min

,

eff

W

- najmniejszy wskaźnik wytrzymałości przekroju współpracującego

0

,

1

0



M



- współczynnik częściowy stosowany przy sprawdzaniu nośności przekroju

poprzecznego

Warunek nośności:

0

,

1

,



Rd

c

Ed

M

M

(6.12)

3.8.Zmiana przekroju poprzecznego podciągu

Zmiany przekroju dokonujemy przez zmianę szerokości pasów wg wzoru:

5





y

f

w

f

s

s

f

f

t

h

t

M

b







,

gdzie: M

m

– moment zginający w miejscu wykonania styku

- Klasa przekroju ze względu na środnik

w

w

t

a

h

t

d

t

c

2

2









- Klasa przekroju ze względu na pas





f

w

s

f

t

a

t

b

t

c

2

5

.

0

,









- moment bezwładności:

I

y,s

[mm

4

]



 



12

12

2

3

,

3

,

,

w

w

s

f

f

s

s

f

s

y

h

t

b

t

h

b

I















- sprężysty wskaźnik wytrzymałości: W

el,y,s

[mm

3

]

h

I

W

s

y

s

y

el

,

,

,

2





3.9.Sprawdzenie nośności przekroju przy ścinaniu

Zgodnie z PN-EN-1993-1-5 p.5.1 środniki nieużebrowane o smukłości









72

w

w

t

h

, oraz

użebrowane o smukłości







k

t

h

w

w







31

, gdzie

y

f

235





, należy usztywnić, żebrami

poprzecznymi na podporach oraz sprawdzić na niestateczność przy ścinaniu. Jeśli to

wymagane, to żebra poprzeczne należy stosować również pod obciążeniami skupionymi i w

miejscach pośrednich.

UWAGA:

W projekcie przyjmujemy podatne żebra podporowe.

Należy założyć, że pomiędzy żebrami na których opierają się belki stropowe znajduje się

jeszcze jedno lub dwa żebra poprzeczne sztywne, rozmieszczone równomiernie na długości

6

- sprawdzenie smukłości środnika







k

t

h

w

w







31

- minimalny parametr niestateczności przy ścinaniu





sl

w

k

a

h

k











2

/

00

,

4

34

,

5

gdy

1

/



w

h

a

(A.5)PN-EN-1993-1-5





sl

w

k

a

h

k











2

/

34

,

5

00

,

4

gdy

1

/



w

h

a

(A.5)PN-EN-1993-1-5

0



sl

k



- jeśli nie występują żebra podłużne

a – rozstaw żeber poprzecznych wg Rysunku 5.3

UWAGA:

W przypadku podatnych żeber poprzecznych minimalną wartość



k uzyskuje się rozpatrując

niestateczność:
1.układu dwóch sąsiednich paneli z jednym żebrem podatnym (a=a

1

+a

2

)

2. układu trzech kolejnych paneli z dwoma żebrami podatnymi (a=a

1

+a

2

+a

3

)

Procedurę wyznaczania



k podano w Załączniku A.3 PN-EN-1993-1-5

Należy również sprawdzić parametr niestateczności dla przypadku gdy a=a

1

- wyznaczenie smukłości względnej płytowej







k

t

h

w

w











4

,

37

(5.5)PN-EN-1993-1-5

- określenie współczynnika niestateczności

w



- określenie nośności obliczeniowej środnika przy ścinaniu

1

,

3

M

w

w

yw

w

Rd

bw

t

h

f

V







gdzie: f

yw

- granica plastyczności środnika

0

,

1

1



M



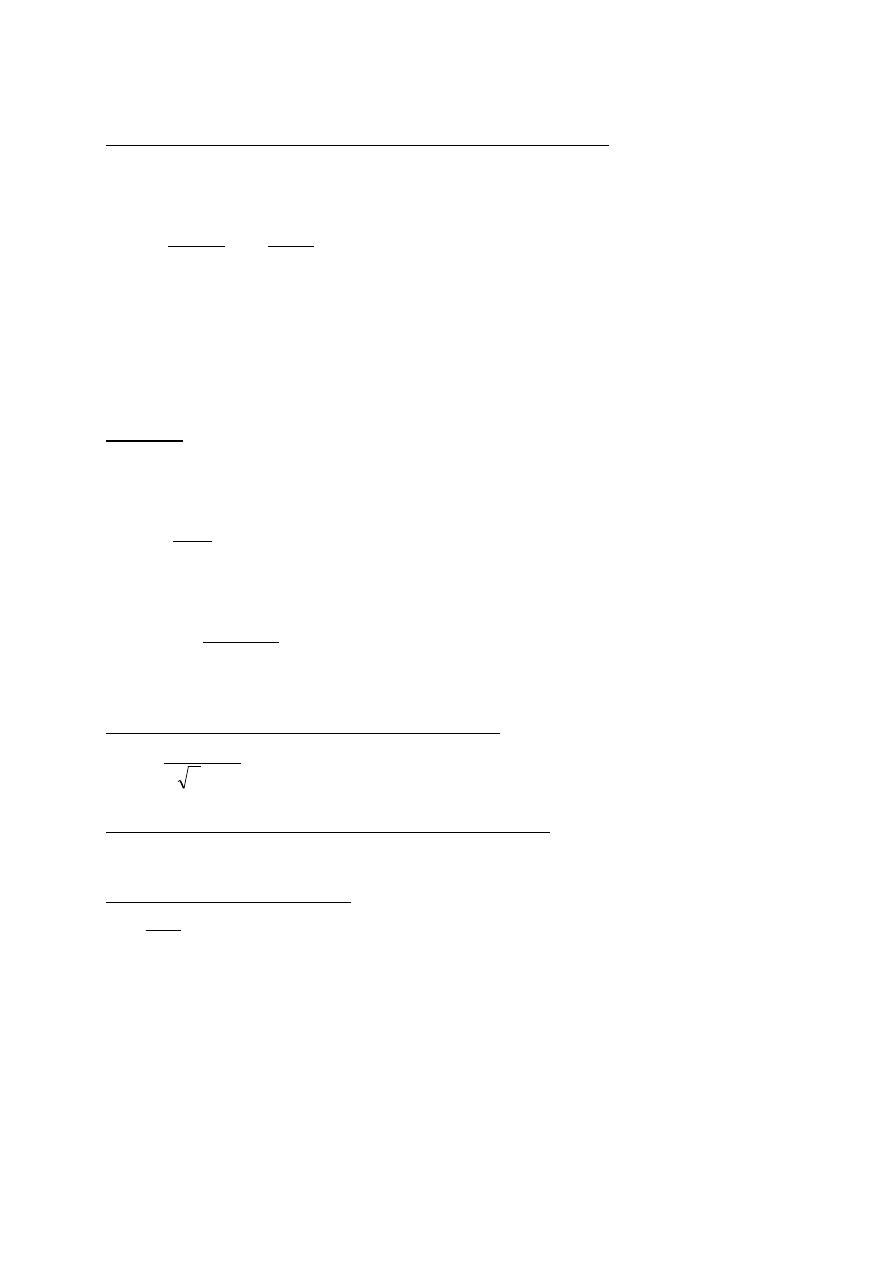
7

- Sprawdzenie udziału pasów w nośności obliczeniowej przy ścinaniu

Jeżeli pasy nie są w pełni wykorzystane do przeniesienia momentu zginającego (M

Ed

.<M

f,,Rd

)

to ich udział w nośności obliczeniowej przy ścinaniu można wyznaczać według wzoru:



































2

,

1

2

,

1

Rd

f

Ed

M

yf

f

f

Rd

bf

M

M

c

f

t

b

V



(5.8) PN-EN-1993-1-5

gdzie:
b

f

i t

f

-wymiary pasa o mniejszej nośności przy obciążeniu siłą podłużna

b

f

-szerokość efektywna pasa, ograniczona z każdej strony środnika do wartości 15ε t

f

f

yf

- granica plastyczności pasa

0

,

1

1



M



UWAGA:

Ponieważ rozpatrujemy przekrój nad podporą to moment M

Ed

=0 - nie musimy wyznaczać

obliczeniowej nośności przy zginaniu przekroju złożonego tylko z efektywnych części pasów
.

0

,

,

M

k

f

Rd

f

M

M





- obliczeniowa nośność przy zginaniu przekroju złożonego tylko z

efektywnych części pasów



















yw

w

w

yf

f

f

f

h

t

f

t

b

a

c

2

2

6

,

1

25

,

0

a – odległość między żebrami poprzecznymi

- Nośność obliczeniowa środnika przy uplastycznieniu

1

,

3

M

w

w

yw

Rd

w

t

h

f

V







(5.2)PN-EN-1993-1-5

- Nośność obliczeniowa przekroju przy ścinaniu blachownicy

Rd

w

Rd

bf

Rd

bw

Rd

b

V

V

V

V

,

,

,

,







(5.1)PN-EN-1993-1-5

- Warunek nośności przy ścinaniu

0

,

1

,

3





Rd

b

Ed

V

V



(5.10)PN-EN-1993-1-5

8

3.10.Stateczność pasa przy smukłym środniku

UWAGA:
Należy tak projektować blachownice, aby zapobiec wyboczeniu pasa ściskanego w
płaszczyźnie środnika.

Dla pasów prostych powinien być spełniony następujący warunek smukłości:

fc

w

yf

w

w

A

A

f

E

k

t

h



(8.1)PN-EN-1993-1-5

gdzie:

A

w

– pole przekroju środnika

A

fc

– efektywne pole przekroju pasa ściskanego

h

w

– wysokość środnika

t

w

– grubość środnika

Wartość parametru k przyjmuje się jak następuje:
-gdy przyjmuje się nośność sprężystą przy zginaniu:

k=0,55 (przekrój klasy 3. lub 4.)

3.10.Interakcja zginania, siły poprzecznej i siły podłużnej

Jeżeli

5

,

0

3





to warunek nośności przekroju przy zginaniu i ścinaniu środnika w dźwigarach

dwuteowych lub skrzynkowych ma postać:





0

,

1

1

2

1

2

3

,

,

1





























Rd

pl

Rd

f

M

M

lecz

Rd

pl

Rd

f

M

M

,

,

1





(7.1)PN-EN-1993-1-5

gdzie:

M

f,Rd

– obliczeniowa nośność przy zginaniu przekroju złożonego tylko z efektywnych części

pasów

M

pl,Rd

– obliczeniowa nośność plastyczna przy zginaniu przekroju złożonego z efektywnych

części pasów oraz w pełni efektywnego środnika niezależnie od jego klasy przekroju





0

0

,

,

M

yf

f

w

f

f

M

k

f

Rd

f

f

t

h

b

t

M

M





















yw

w

w

yf

f

w

f

f

Rd

pl

f

t

h

f

t

h

b

t

M





























2

,

2

gdzie:
f

y,f

- granica plastyczności pasa

f

y,w

- granica plastyczności środnika

Rd

pl

Ed

M

M

,

1





Rd

bw

Ed

V

V

,

3





9

gdzie:
V

bw,Rd

– obliczeniowa nośność środnika przy ścinaniu

UWAGA:

Nośność na ścinanie sprawdzamy dla przekroju podporowego. Jeżeli więc

5

,

0

3





dla

przekroju podporowego, to możemy przyjąć, że jest to też sprawdzenie dla środka rozpiętości
podciągu.

3.11.Nośność środnika pod obciążeniem skupionym –
3.12.Sprawdzenie podatnego żebra podporowego

Żebro podporowe powinno być zaprojektowanie wg. PN-EN-1993-1-5 p.9.1.

- wymiary żebra
szerokość:

?????



s

b

grubość:

?????



s

t

UWAGA:
Należy tak dobrać wymiary żebra aby były klasy 1,2 lub 3.

- szerokość współpracująca środnika

t

b

ws



15



Siłę podłużną w żebrze poprzecznym przyjmuje się równą sumie siły poprzecznej i
ewentualnych obciążeń zewnętrznych (p.9.1(3) PN-EN-1993-1-5)

-powierzchnia współpracująca:





w

s

w

s

s

st

t

t

t

t

b

A









30

2

-moment bezwładności:









12

30

5

,

0

5

,

0

12

2

2

2

3

w

s

w

w

s

s

s

s

s

st

t

t

t

t

b

b

t

b

t

I

























-promień bezwładności:

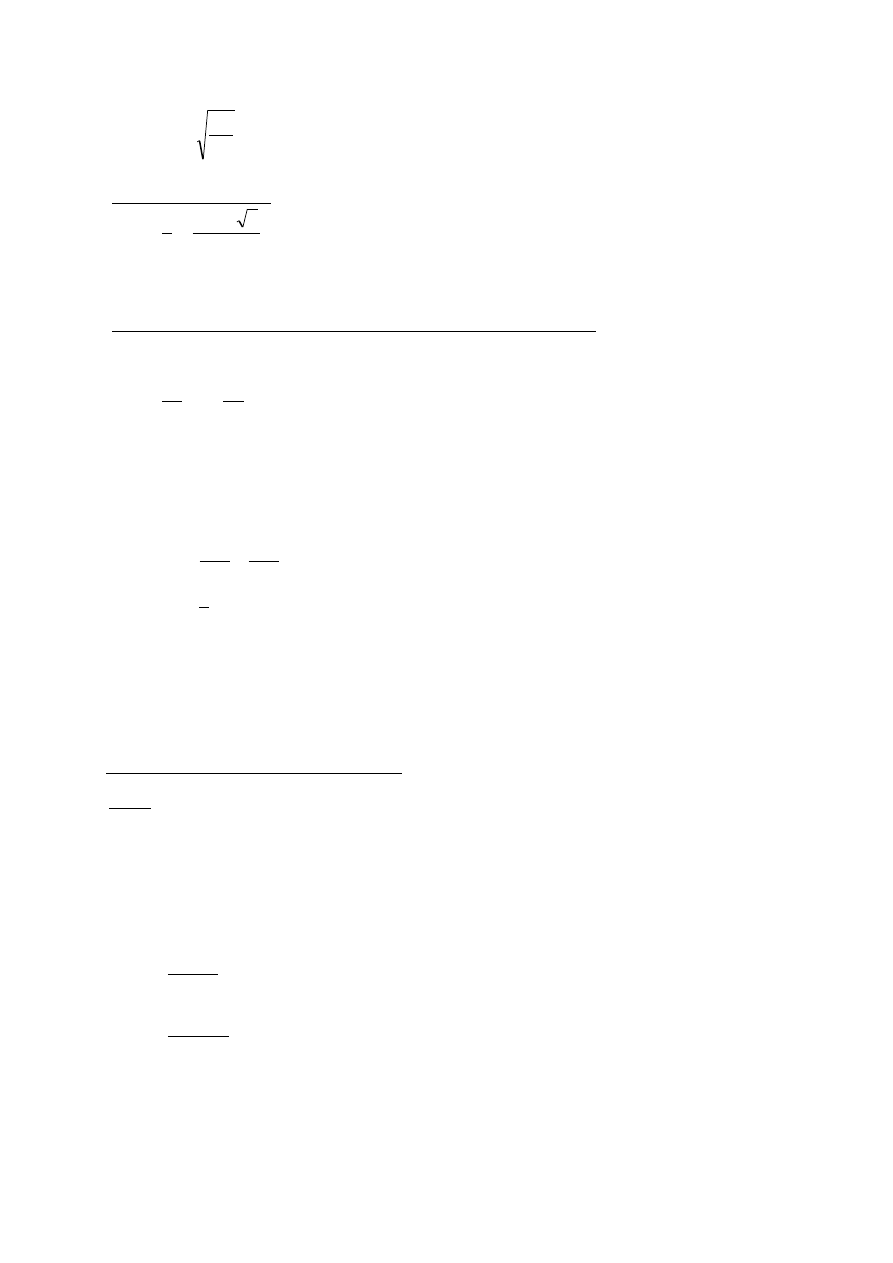
10

st

st

st

A

I

i



-klasa przekroju żebra:

s

s

t

a

b

t

c

2





-sprawdzenie stateczności żebra ze względu na wyboczenie skrętne:

Stateczność żebra na wyboczenie skrętne jest zapewniona, gdy spełniony jest warunek:

E

f

I

I

y

p

T

3

,

5



(9.3)PN-EN-1993-1-5

gdzie:
I

p

– biegunowy moment bezwładności przekroju żebra względem punktu styczności ze

ścianką
I

T

– moment bezwładności przekroju żebra przy skręcaniu swobodnym (ST.Venanta)

12

3

3

3

s

s

s

s

P

t

b

b

t

I





3

3

1

s

s

T

t

b

I



gdzie:
bs – długość żebra
ts - szerokość żebra



-nośność i stateczność żebra na ściskanie

0

,

1

N

N

Rd

,

b

Ed



(6.46), gdzie:

N

Ed

– obliczeniowa siła ściskająca – w naszym przypadku N

Ed

=V

Ed

N

b,Rd

– nośność na wyboczenie elementu ściskanego.

1

M

y

Rd

,

b

f

A

N







- w przypadku przekrojów klasy 1, 2 i 3 (6.47)

1

M

y

eff

Rd

,

b

f

A

N







- w przypadku przekrojów klasy 4 (6.48)

gdzie:



- współczynnik wyboczenia, odpowiadający miarodajnej postaci wyboczenia.



M1

= 1.0 – wsp. częściowy przy ocenie stateczności

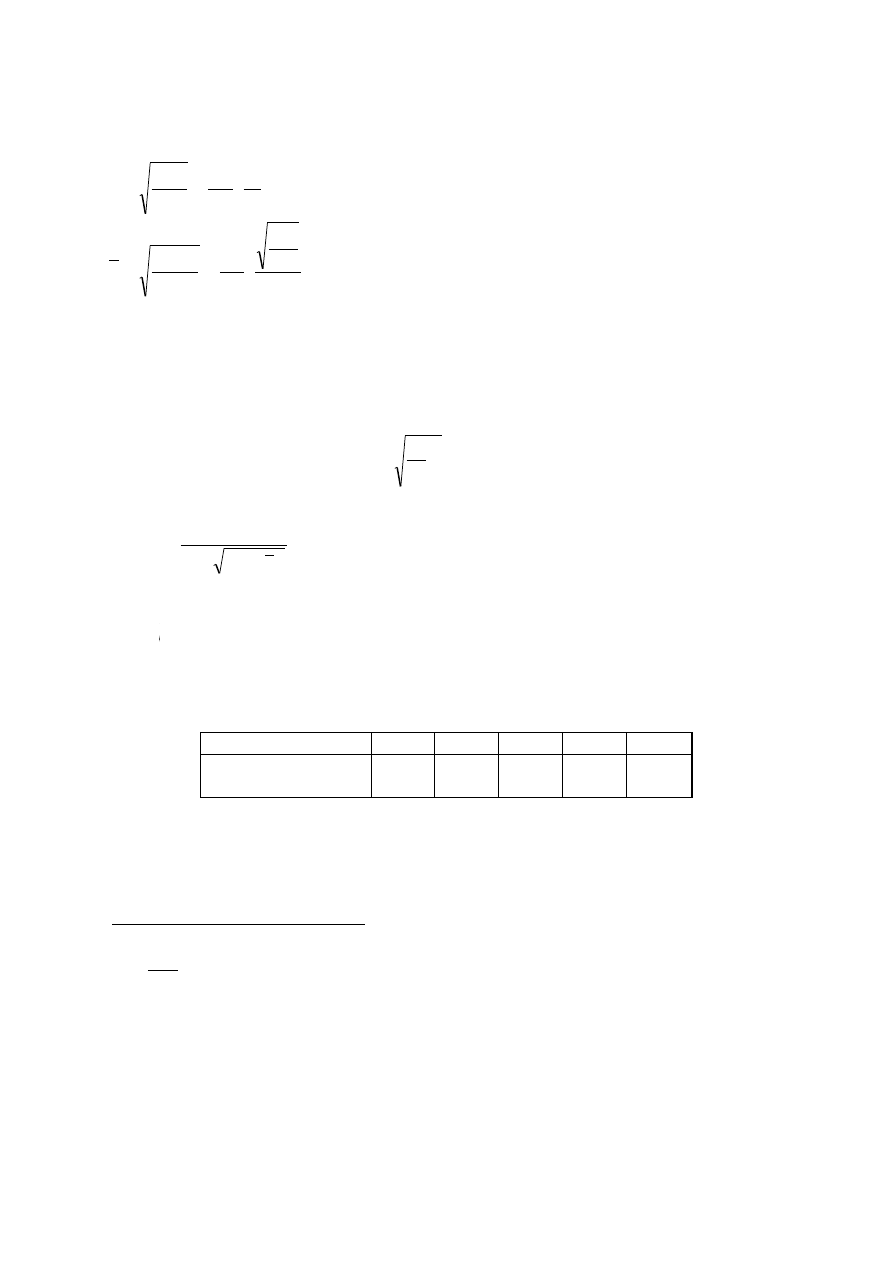
11

A=A

s

– pole przekroju współpracującego żebra

1

1













i

L

N

f

A

cr

cr

y

- dla przekrojów klasy 1,2 lub 3.

(6.50) PN-EN-1993-1-1)

1





A

A

i

L

N

f

A

eff

cr

cr

y

eff







- dla przekrojów klasy 4.

(6.51) PN-EN-1993-1-1)

N

cr

- siła krytyczna odpowiadająca miarodajnej postaci wyboczenia sprężystego,

wyznaczona na podstawie cech przekroju brutto.

cr

L

- długość wyboczeniowa;

w

cr

h

L

75

,

0



st

i

i



- promień bezwładności żebra

st

A

A



- pole przekroju poprzecznego żebra

1



-

smukłość porównawcza:







9

,

93

1





y

f

E



Obliczenie współczynnika wyboczeniowego

2

2

1















lecz

0

,

1









1,0 (6.49) PN-EN-1993-1-1)

gdzie:



2

2,015,0





























































2

2

,

0

1

5

,

0



- parametr imperfekcji (tabl.6.1)

Tablica 6.1: Parametry imperfekcji krzywych wyboczenia

Krzywa wyboczenia

a

0

a

b

c

d

Parametr imperfekcji



0,13

0,21

0,34

0,49

0,76

Współczynnik wyboczeniowy



- można obliczyć wg procedury jak w projekcie słupa

-sprawdzenie docisku żebra do pasa

y

d

Ed

d

f

A

N







gdzie:
A

d

– powierzchnia docisku żeber do pasa





s

s

s

d

t

c

b

A







2

gdzie:
c

s

– ścięcie żebra przy styku z pasem

12

bs – szerokość żebra



3.14.Sprawdzenie naprężeń w spoinach łączących półki ze środnikiem

- przyjęcie spoin łączących środnik z pasem

min

max

7

,

0

2

,

0

t

a

t







oraz

mm

3



a

UWAGA:
Spoiny były przyjęte na początku obliczeń podciągu. Należy teraz zweryfikować ich nośność.

- obliczeniowa nośność spoiny na ścinanie

2

3

/

M

w

u

vw

f

f









(4.4)PN-EN-1993-1-8

gdzie:

25

,

1

2



M



- współczynnik częściowy stosowany przy sprawdzaniu nośności spoin

w



- współczynnik korelacji zależny od gatunku stali

- naprężenia w spoinach

a

I

S

V

y

y

Ed

II









2



gdzie:



















2

,

w

f

s

f

y

h

t

b

S

- moment statyczny na styku środnika i pasa względem środka ciężkości

przekroju

s

y

y

I

I

,



- moment bezwładności zmniejszonego przekroju

a – grubość spoiny

- warunek nośności

vw

II

f





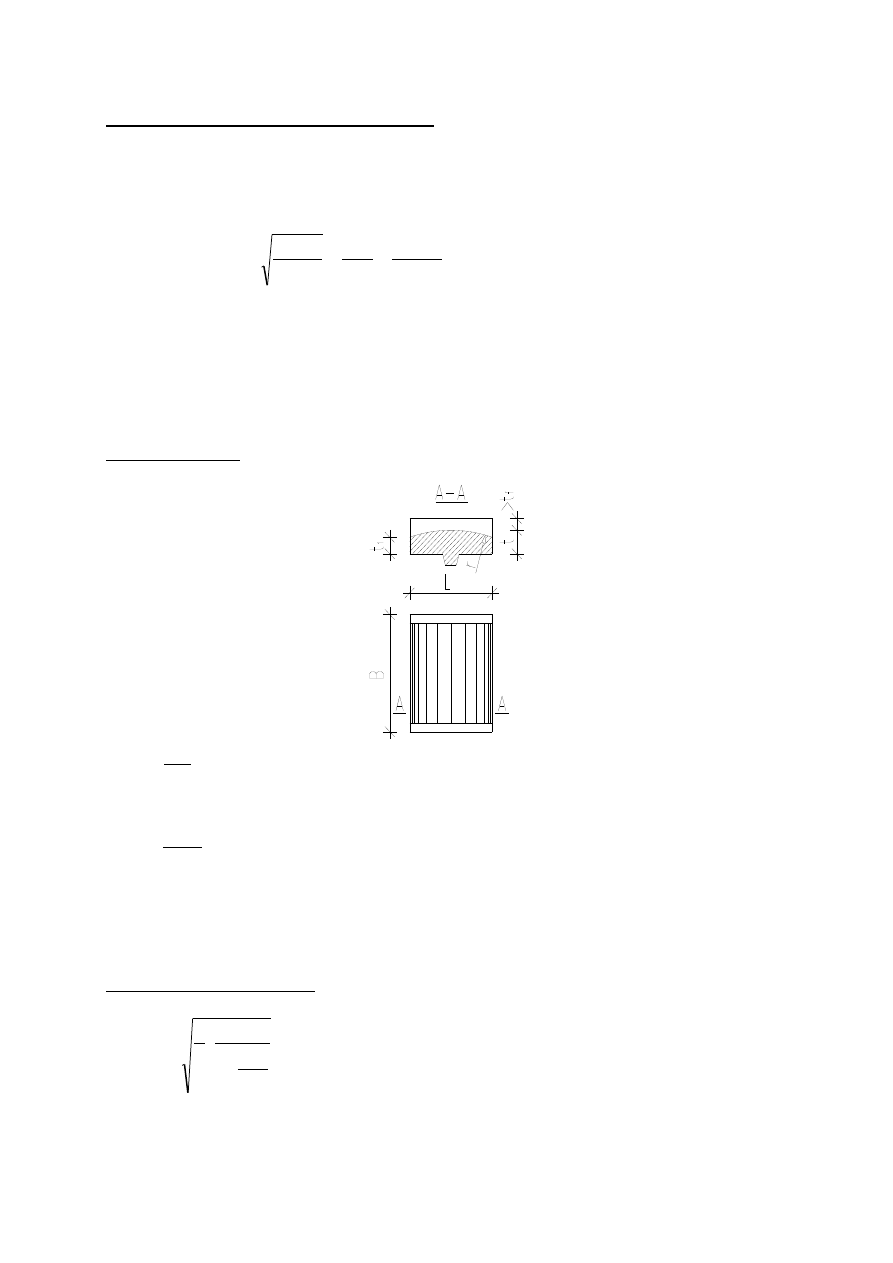
13

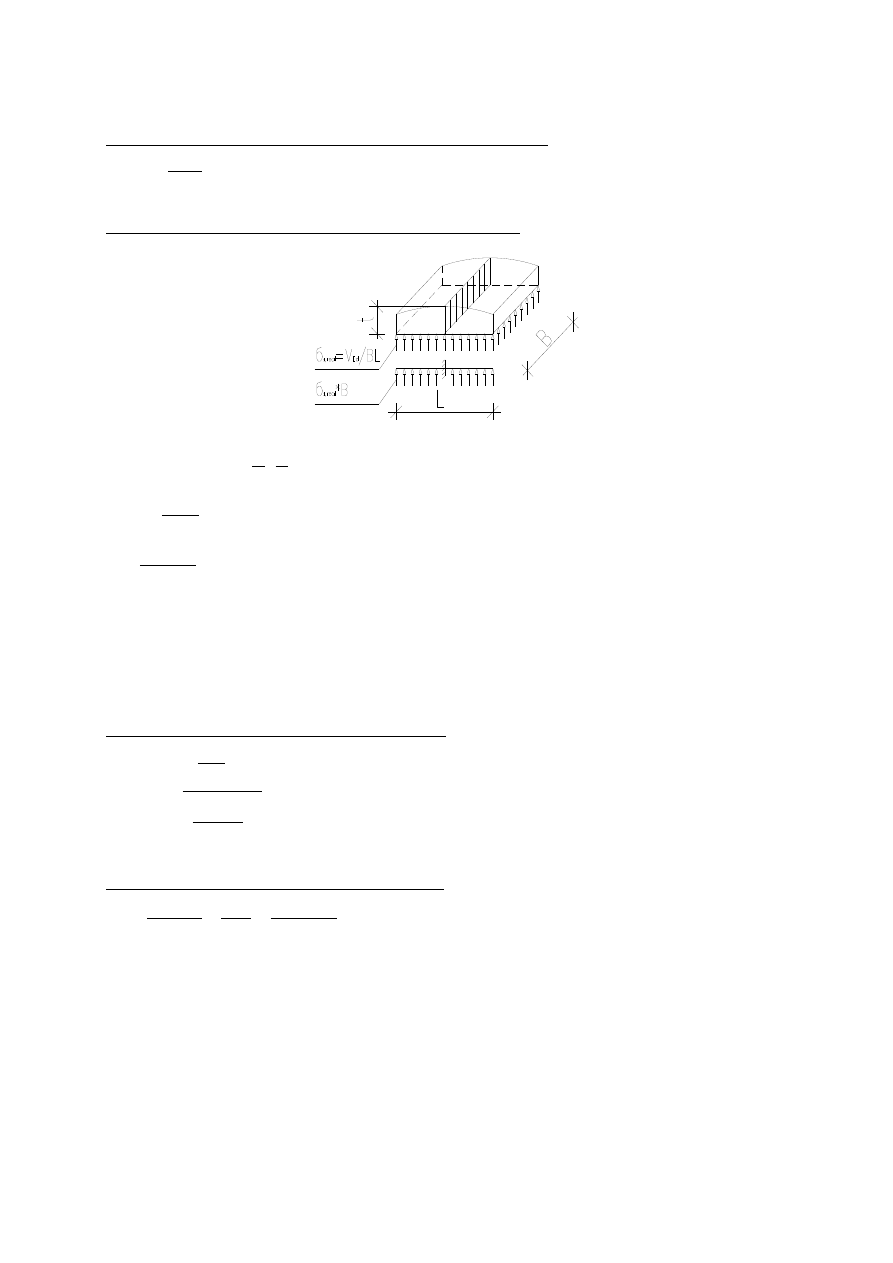
3.14. Zaprojektowanie łożyska podporowego

W przypadku projektowania łożyska stycznego minimalny promień krzywizny łożyska (płyty
dolnej) oblicza się na podstawie wzoru Hertza, z warunku docisku przy swobodnym dotyku
powierzchni płaskiej i cylindrycznej.

0

0

,

6

,

3

42

,

0

M

y

M

ylb

f

Ed

ylb

Hertz

b

f

f

r

b

E

V

























gdzie:
V

Ed

– obliczeniowa reakcja dźwigara

b

f

– szerokość łożyska

E – współczynnik sprężystości stali
f

ylb

– wytrzymałość obliczeniowa stali na docisk określana wg wzoru Hertza

y

ylb

f

f





6

,

3

- wymiary łożyska

cd

Ed

req

b

f

V

A



,

f

w

f

t

t

b

B

B













2

2

min

B

A

L

req

b

req

b

,

,



gdzie:
A

b,req

– minimalna powierzchnia docisku

B

min

– minimalna szerokość łożyska

L

b,req

– minimalna długość łożyska

- minimalna grubość łożyska

0

,

4

3

M

y

Ed

req

b

f

B

L

V

t

t













t

t





75

,

0

1

14

- sprawdzenie naprężeń przekazywanych na podporę (ścianę)

cd

Ed

real

b

f

L

B

V







,



- sprawdzenie naprężeń w płaszczyźnie środowej łożyska

4

2

,

max,

L

L

B

M

real

b

Ed











4

2

,

t

B

W

pl

b





y

pl

b

Ed

f

W

M





,

max,



gdzie:
M

max,Ed

– obliczeniowy moment zginający w środku łożyska

W

b,pl

– plastyczy wskaźnik wytrzymałości łożyska

σ – naprężenia w środku łożyska

- wyznaczenie minimalnego promienia łożyska

2

0

6

,

3

176

,

0





















M

y

f

Ed

f

E

b

V

r



- sprawdzenie docisku do powierzchni płaskiej

0

0

25

,

1

2

M

ysb

M

ysb

f

Ed

b

f

f

b

r

V

















