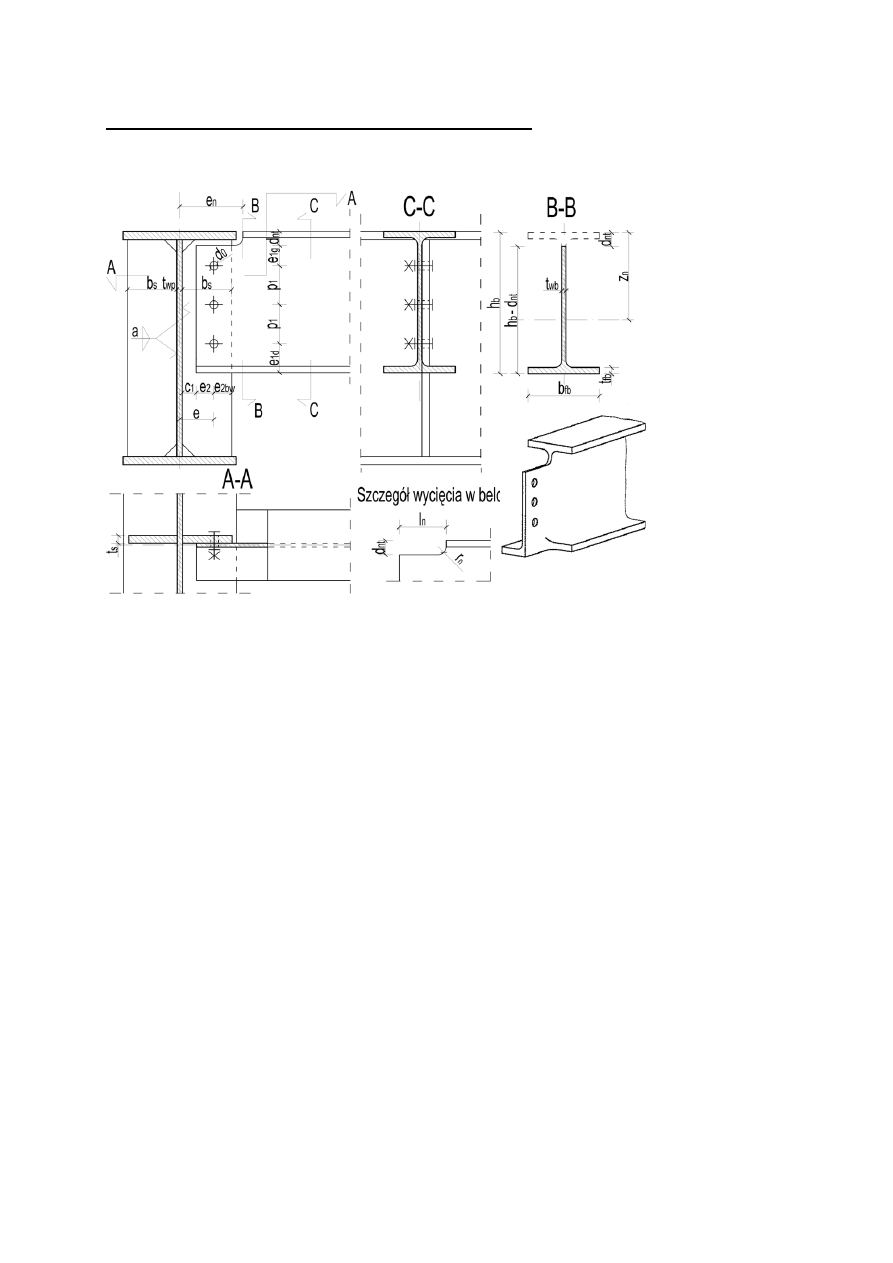
Połączenie belki z podciągiem – sem. 5 - przykład

Dane:
• Gatunek stali elementów:

f

y

(granica plastyczności), f

u

(wytrzymałość na rozciąganie)

• Obliczeniowa reakcja od belki stropowej: V

Ed

• Blacha węzłowa (żebro):

Blachę węzłową stanowi żebro o takich samych wymiarach jak

zaprojektowane w blachownicy żebro podporowe/pośrednie.
t

s

- grubość żebra

b

s

- szerokość żebra

a - spoina łącząca blachę węzłową (żebro) ze środnikiem podciągu

• Wymiary przekroju belki stropowej:

h

b

(wysokość przekroju), t

wb

(grubość środnika), b

fb

(szerokość

pasa), t

fb

(grubość pasa), r

b

(promień wyokrąglenia)

• Wymiary przekroju podciągu:

h

p

(wysokość przekroju), t

wp

(grubość środnika), b

fp

(szerokość

pasa), t

fp

(grubość pasa) – przyjąć wymiary blachownicy z części

środkowej blachownicy (o szerszych pasach)

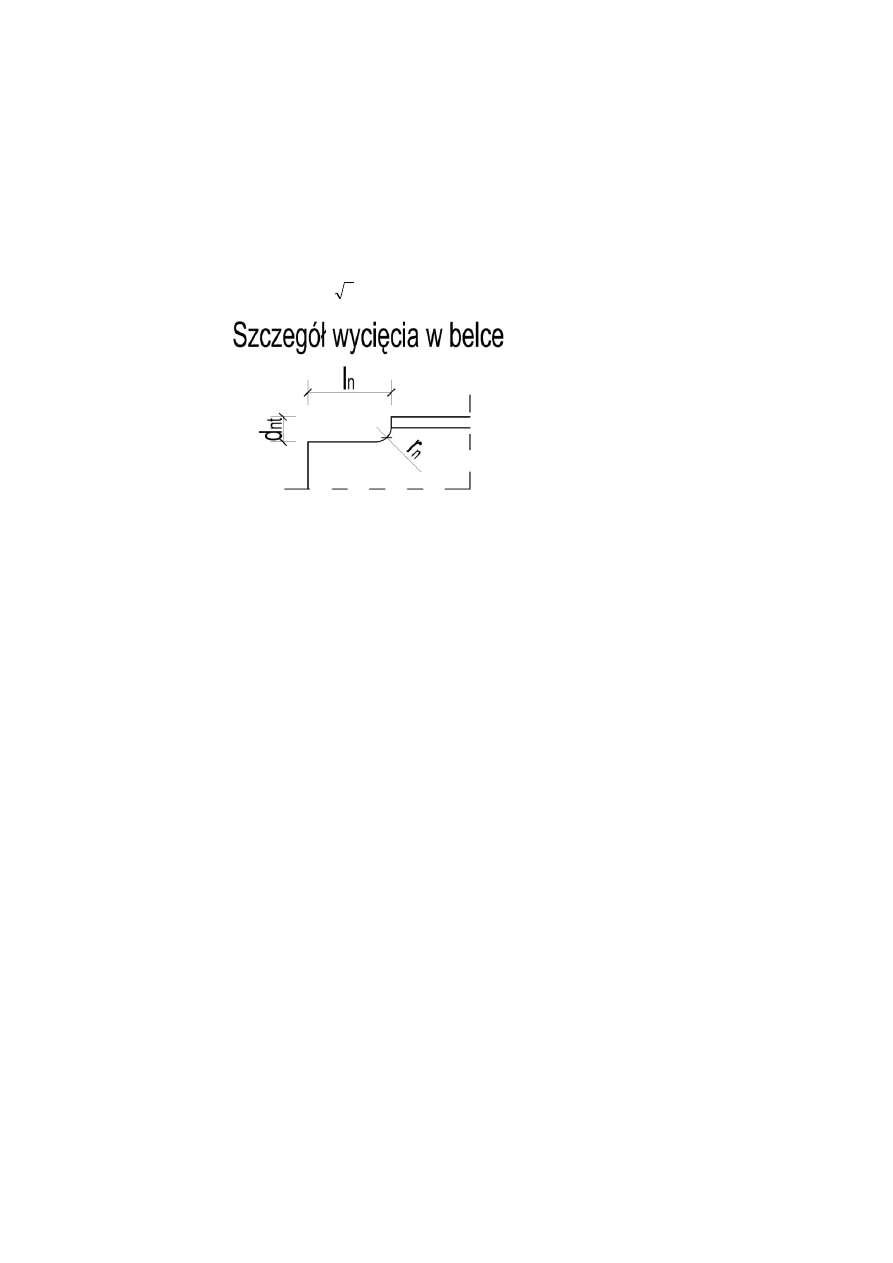
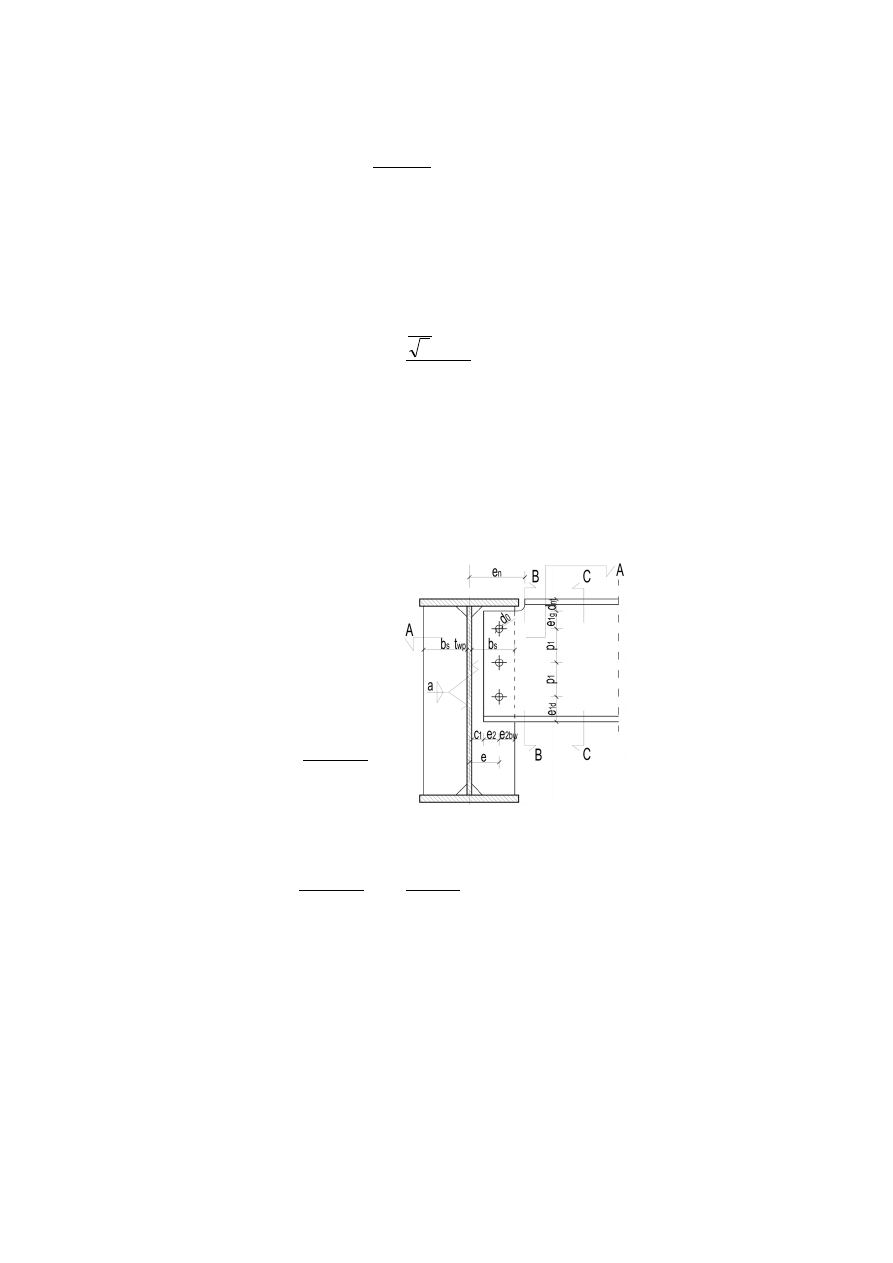
5.1 Wycięcie w belce.

• Szerokość wycięcia: d

nt

> t

fp

+ r

b

• Długość wycięcia: l

n

> 0,5(b

fp

- t

wp

)

• Promień wycięcia: r

n

≈ r

b

• Odległość między krawędzią belki, a środnikiem podciągu:

mm

a

c

10

2

1







• Średnica otworu na śrubę:

d

0

= d + 3mm; dla śrub o średnicy: d ≥ 24mm

d

0

= d + 2mm; dla śrub o średnicy: 14mm ≤ d < 24mm

d

0

= d + 1mm; dla śrub o średnicy: d < 14mm

W przypadku śrub M16: d

0

= d + 2mm = 16 + 2 =18mm

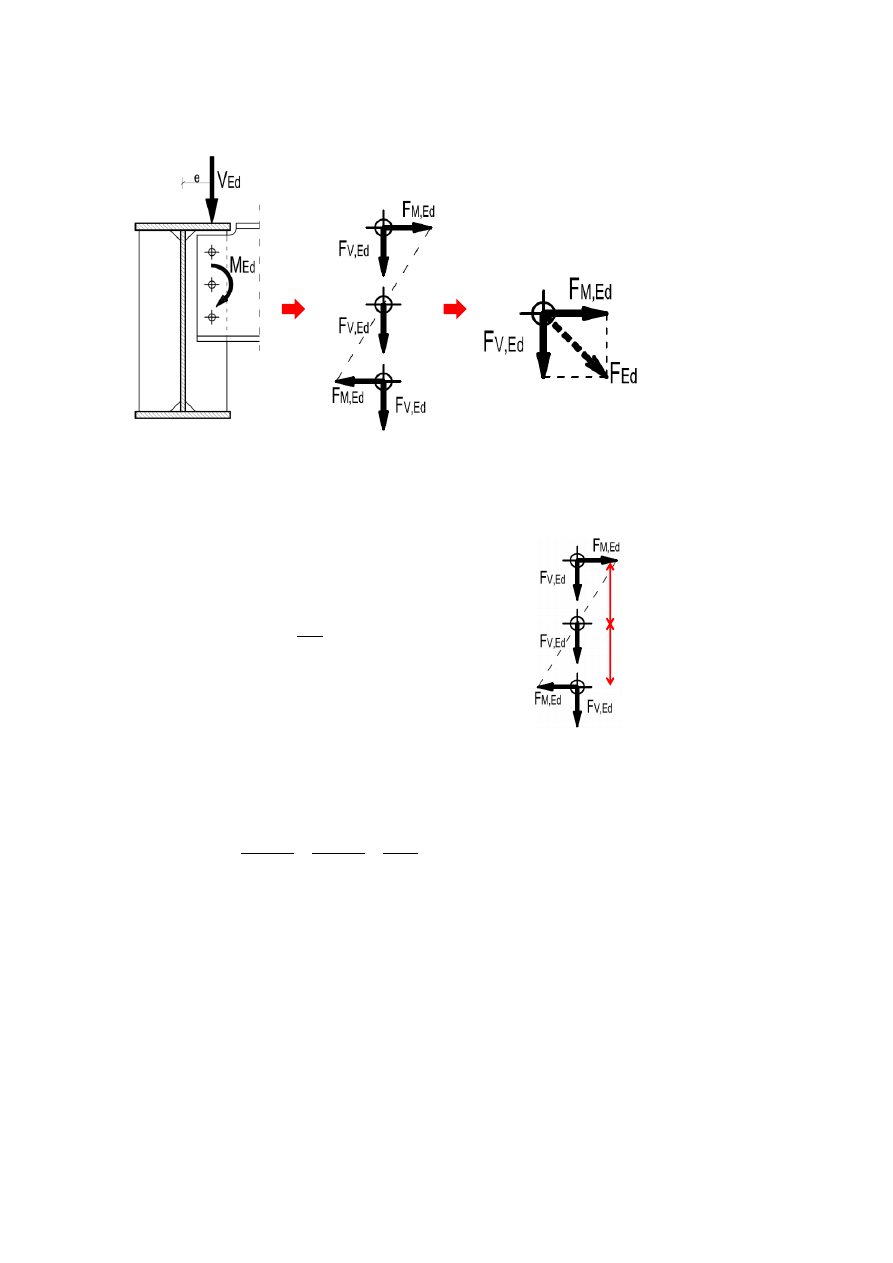
Składowe sił w śrubach

Siły w skrajnej śrubie

(najbardziej wytężonej)

• Składowe sił w śrubach:
o

Składowa od działania siły poprzecznej, jest rozłożona

równomiernie na wszystkie śruby:

gdzie: n jest liczbą śrub w połączeniu

(w tym przypadku n = 3)

n

V

F

Ed

Ed

V



,

1

2

1

2

1

1

2

1

,

2

)

(

r

M

r

r

r

M

r

r

M

F

Ed

Ed

i

Ed

Ed

M

















r

1

r

1

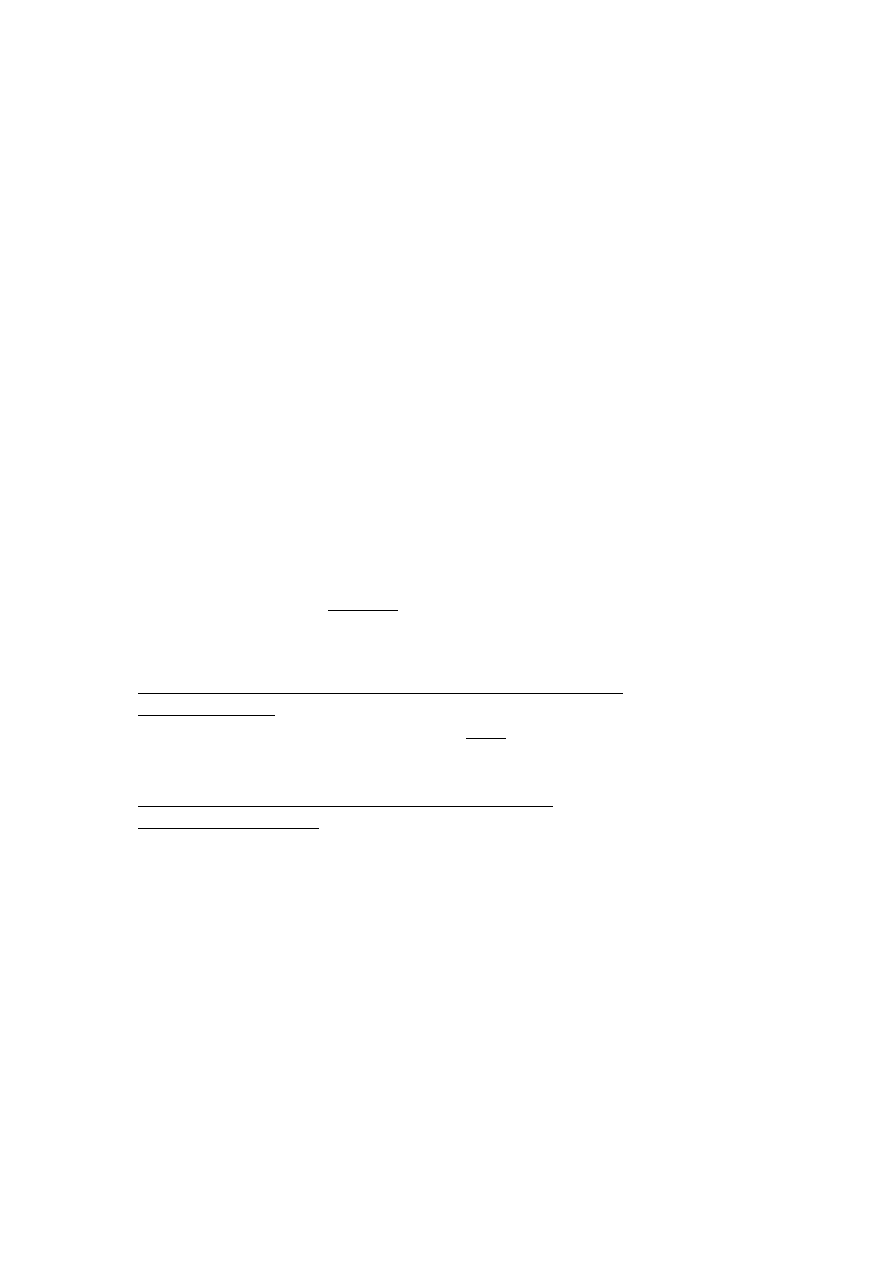
5.4 Sprawdzenie nośności śrub w połączeniu.

Dla połączenia śrubowego, zakładkowego kategorii A (typu

dociskowego) należy sprawdzić (Tablica 3.2, PN-EN 1993-1-8):

F

Ed

≤ F

v,Rd

F

Ed

≤ F

b,Rd

gdzie:

F

Ed

– obliczeniowe obciążenie w najbardziej wytężonej śrubie

(najbardziej oddalonej od środka ciężkości grupy śrub)
F

v,Rd

– obliczeniowa nośność na ścinanie pojedynczej śruby

F

b,Rd

– obliczeniowa nośność pojedynczej śruby na docisk do otworu

5.4.1 Obliczeniowa nośność na ścinanie pojedynczej śruby.

Wg Tablicy 3.4, PN-EN 1993-1-8):

gdzie:

– częściowy współczynnik bezpieczeństwa

W przypadku, gdy płaszczyzna ścinania nie przechodzi przez część
gwintowaną śruby:

A – pole przekroju trzpienia śruby;

W przypadku, gdy płaszczyzna ścinania przechodzi przez
gwintowaną część śruby:

– pole przekroju czynnego śruby

– dla śrub klas 4.6, 5.6, 8.8

– dla śrub klas 4.8, 5.8, 6.8, 10.9

2

,

M

ub

v

Rd

v

A

f

F











25

,

1

2



M



4

2

d

A







s

A

A



6

,

0



v



6

,

0



v



5

,

0



v



5.4.2. Obliczeniowa nośność na docisk pojedynczej śruby.

Wg Tablicy 3.4, PN-EN 1993-1-8):

gdzie:

– częściowy współczynnik bezpieczeństwa

k

1

– współczynnik uwzględniający rozstaw śrub w kierunku

prostopadłym do obciążenia (

*

)

– współczynnik uwzględniający model zniszczenia złącza (

*

)

f

ub

, f

u

– wytrzymałość na rozciąganie materiału śrub i materiału

łączonych elementów

d – średnica trzpienia śruby

d

0

– średnica otworu na śrubę

t – mniejsza z grubości t

wb

i t

s

(grubość żebra)

e

1

, e

2

, p

1

, p

2

– wymiary geometryczne złącza

2

1

,

M

u

b

Rd

b

t

d

f

k

F















25

,

1

2



M



b





W kierunku obciążenia przyjmuje się:

Dla śrub skrajnych:

Dla śrub pośrednich:



Prostopadle do kierunku obciążenia przyjmuje się:

Dla śrub skrajnych:

Dla śrub pośrednich:















0

,

1

;

;

3

min

0

1

u

ub

b

f

f

d

e



















0

,

1

;

;

4

1

3

min

0

1

u

ub

b

f

f

d

p

























5

,

2

7

,

1

4

,

1

7

,

1

8

,

2

min

0

2

0

2

1

d

p

d

e

k



















5

,

2

;

7

,

1

4

,

1

min

0

2

1

d

p

k

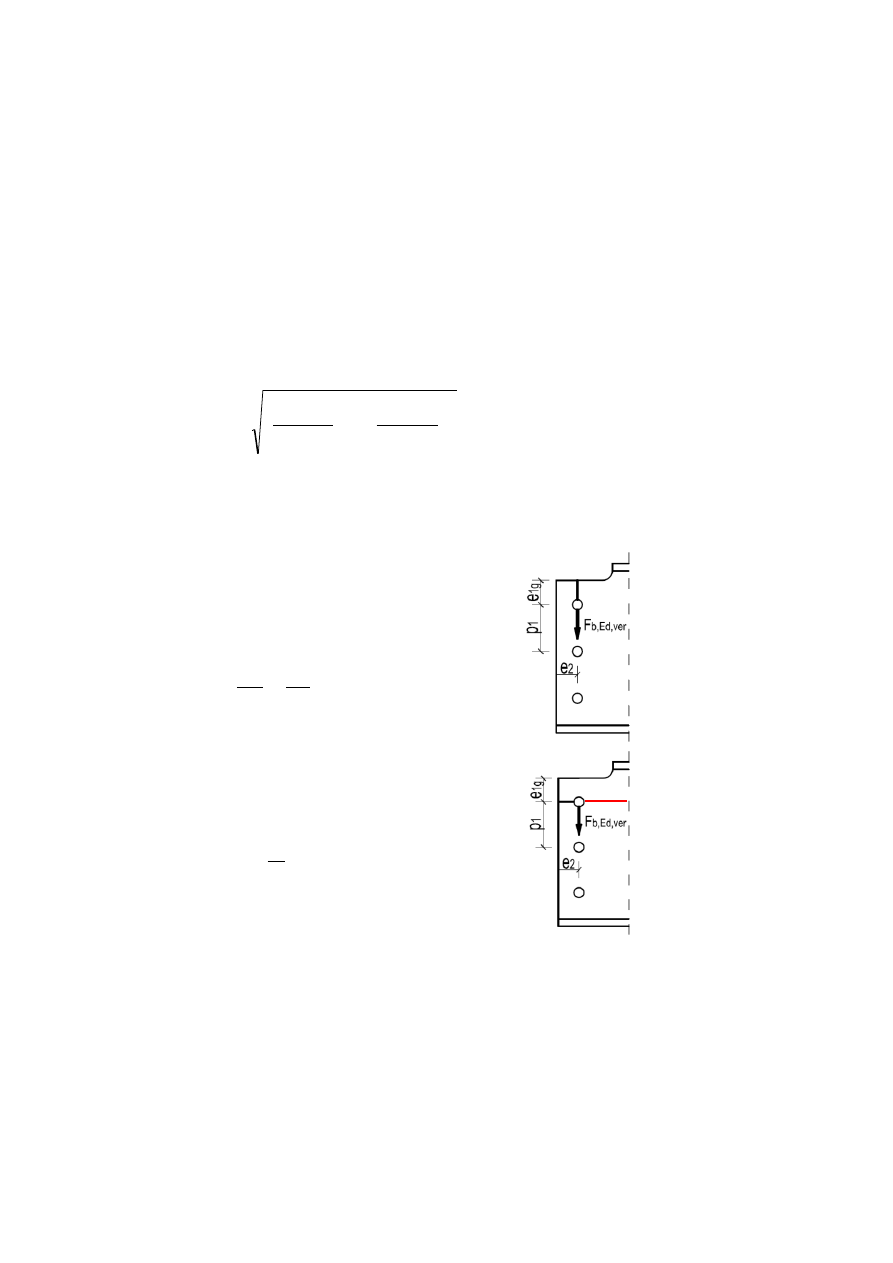
Warunek nośności interakcyjnej:

0

,

1

2

,

,

,

,

2

,

,

,

,

































hor

Rd

b

hor

Ed

b

ver

Rd

b

ver

Ed

b

F

F

F

F

 W kierunku obciążenia :

Dla śrub skrajnych:

 Prostopadle do kierunku obciążenia:

Dla śrub skrajnych:















0

,

1

;

;

3

min

0

1

u

ub

g

b

f

f

d

e





















5

,

2

7

,

1

8

,

2

min

0

2

1

d

e

k

5.4.2.1 Nośność na docisk w kierunku pionowym blachy F

b,Rd,ver

.

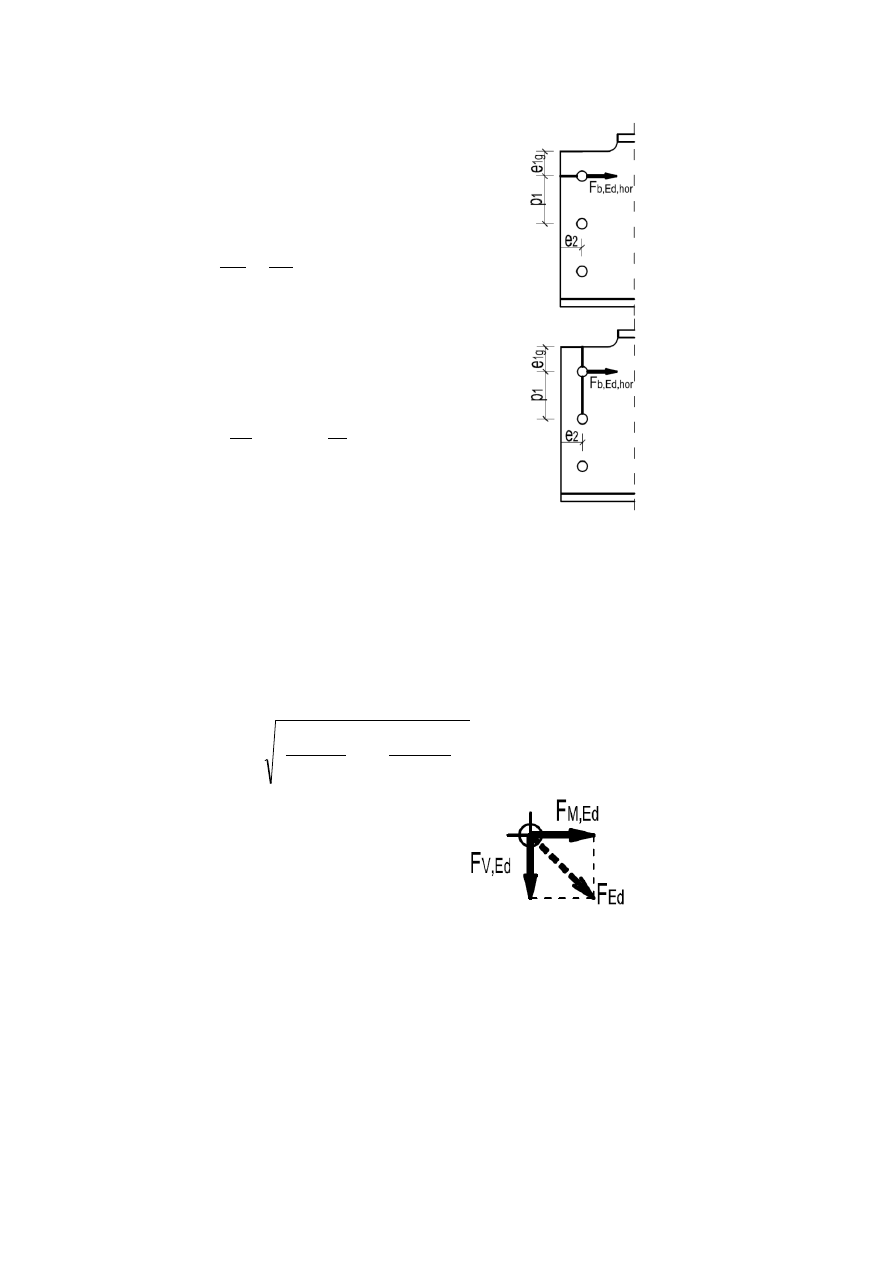
 W kierunku obciążenia:

Dla śrub skrajnych:

 Prostopadle do kierunku obciążenia:

Dla śrub skrajnych:















0

,

1

;

;

3

min

0

2

u

ub

b

f

f

d

e

























5

,

2

7

,

1

4

,

1

7

,

1

8

,

2

min

0

1

0

1

1

d

p

d

e

k

g

5.4.2.2 Nośność na docisk w kierunku poziomym blachy F

b,Rd,hor

.

5.4.3 Sprawdzenie nośności najbardziej wytężonej śruby.

• Jeżeli: F

v,Rd

< min(F

b,Rd,hor

; F

b,Rd,ver

) :

F

Ed

≤ F

v,Rd

• Jeżeli: F

v,Rd

> min(F

b,Rd,hor

; F

b,Rd,ver

) :

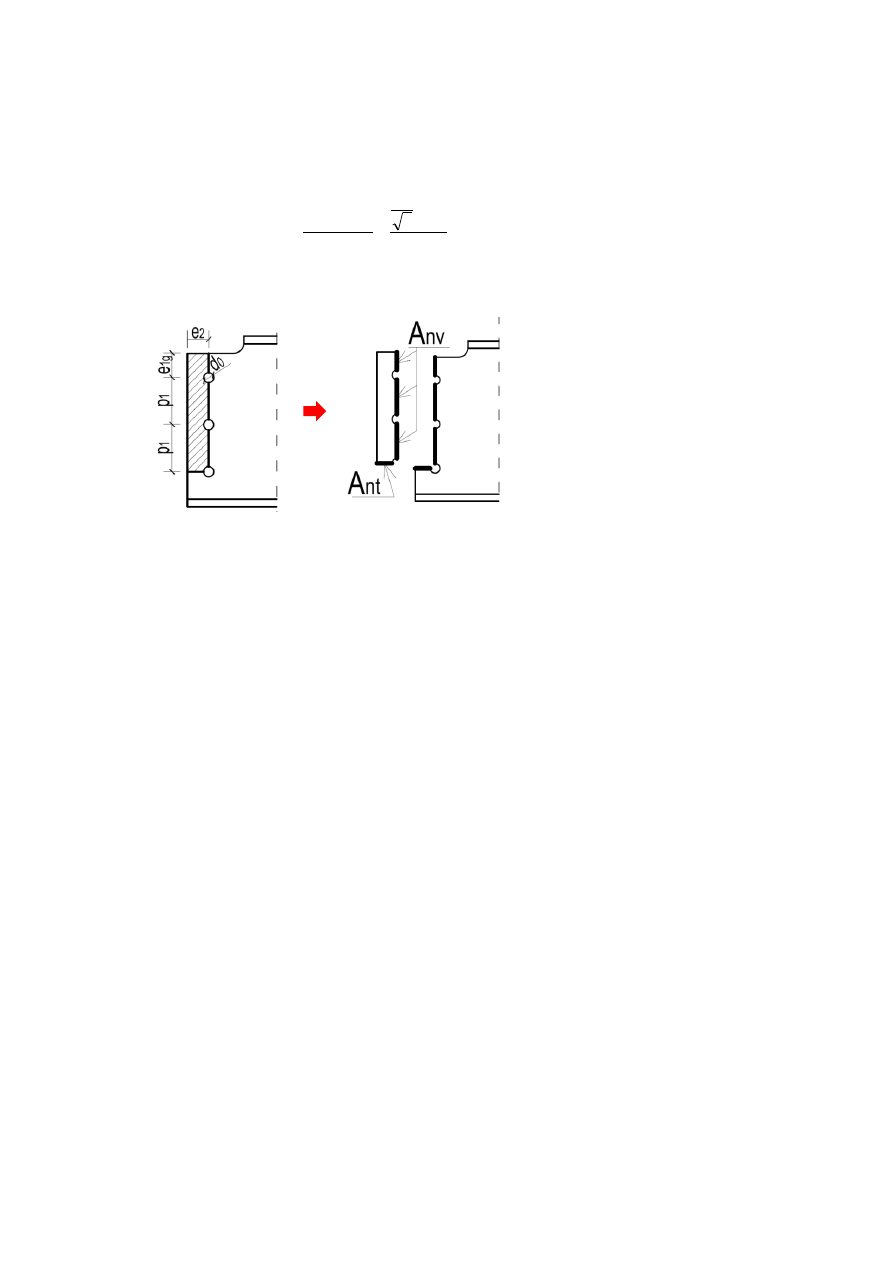
gdzie:

F

b,Ed,hor

= F

M,Ed

F

b,Ed,ver

= F

V,Ed

0

,

1

2

,

,

,

,

2

,

,

,

,

































hor

Rd

b

hor

Ed

b

ver

Rd

b

ver

Ed

b

F

F

F

F

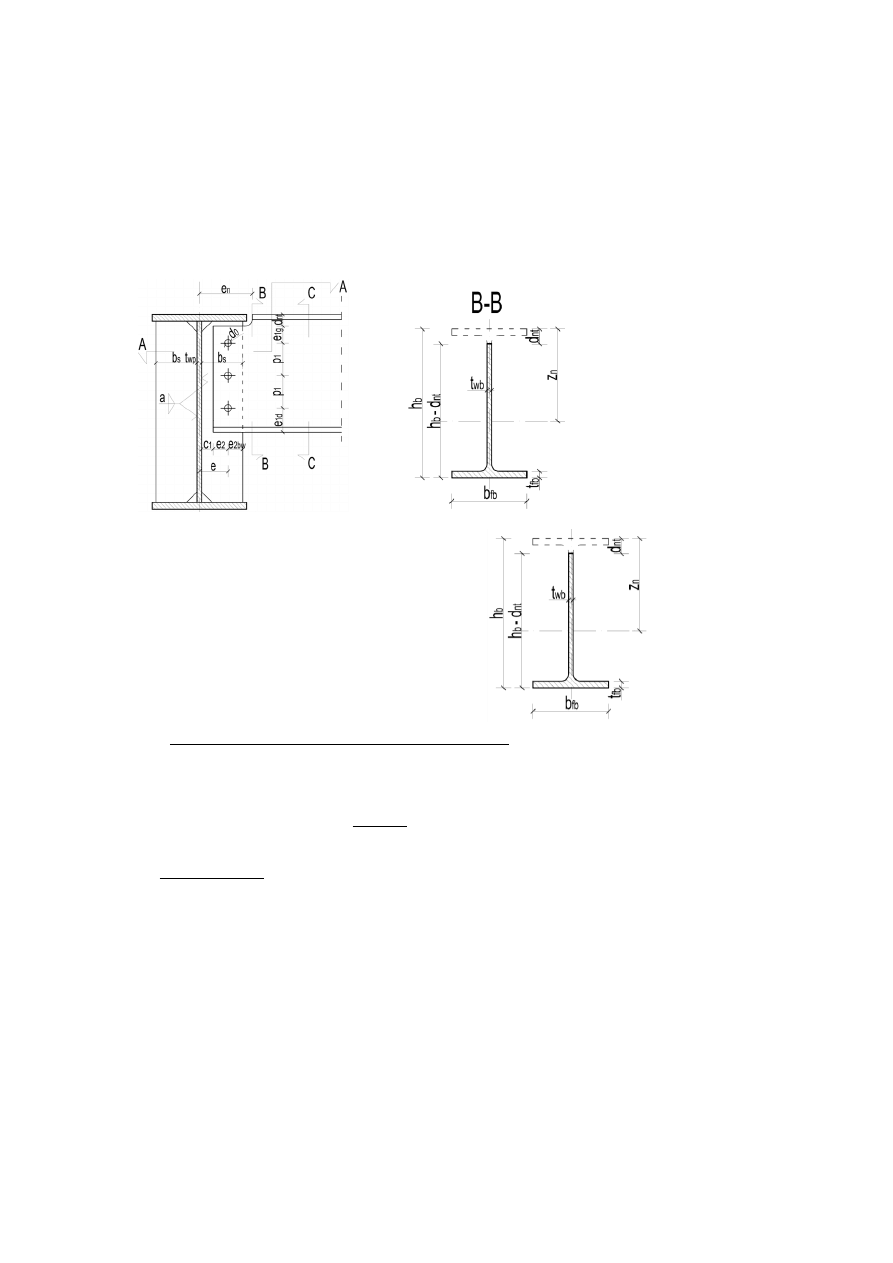
5.5 Sprawdzenie nośności na rozerwanie blokowe (pkt. 3.10.2).
• W przypadku grupy śrub obciążonej mimośrodowo, obliczeniowa
nośność na rozerwanie blokowe wynosi:

Przekrój netto rozciągany A

nt

= t

wb

(e

2

– 0,5d

0

), (

*

)

Przekrój netto ścinany A

nv

= t

wb

(e

1g

+ 2p

1

– 2,5d

0

), (

*

)

0

2

,

2

,

3

5

,

0

M

nv

y

M

nt

u

Rd

eff

A

f

A

f

V













(

*

) Wzory są ważne tylko dla 3 śrub w jednym szeregu (przy zmianie

liczby śrub i/lub liczby szeregów śrub, należy odpowiednio
wyznaczyć A

nt

i A

nv

, wg Rysunku 3.8 w PN-EN 1993-1-8)

Warunek nośności:

V

Ed

≤ V

eff,2,Rd

5.6 Sprawdzenie nośności przekroju belki stropowej osłabionego
wycięciem.
• Sprawdzenie nośności przekroju

5.6.1 Charakterystyki geometryczne.

- Pole przekroju belki stropowej z wycięciem:

A

n

= A

b

– b

fb

t

fb

– (d

nt

– t

fb

) t

wb

A

b

– całkowity przekrój belki stropowej (dane)

- Wyznaczenie położenia środka ciężkości

przekroju z wycięciem od górnej krawędzi pasa
górnego belki (z

n

):

- Moment bezwładności przekroju belki z wycięciem:

n

wb

fb

nt

fb

fb

fb

b

b

n

A

t

t

d

t

b

t

A

h

z























)

(

5

,

0

)

(

5

,

0

5

,

0

2

2

2

3

2

3

2

)

5

,

0

5

,

0

(

)

(

12

)

(

)

5

,

0

(

12

)

5

,

0

(

fb

nt

n

wb

fb

nt

fb

nt

wb

fb

n

fb

fb

fb

fb

b

n

b

yb

n

t

d

z

t

t

d

t

d

t

t

z

t

b

t

b

h

z

A

I

I

















































I

yb

– moment bezwładności całkowitego przekroju belki stropowej

- Wskaźnik wytrzymałości:

- Przekrój czynny przy ścinaniu:

A

v,n

= 0,9(A

n

– b

fb

t

fb

)

5.6.2 Sprawdzenie nośności przekroju na ścinanie.

nt

n

n

n

el

d

z

I

W





,

0

,

,

,

3

M

n

v

y

Rd

pl

n

Ed

A

f

V

V









5.6.3 Sprawdzenie nośności przekroju na zginanie.
• moment zginający M

n,Ed

= V

Ed

e

n

• mimośród

gdzie: l

n

– długość wycięcia belki

Warunek nośności:
• Jeżeli V

Ed

≤ 0,5V

n,pl,Rd

• Jeżeli V

Ed

> 0,5V

n,pl,Rd

Należy uwzględnić interakcję zginania ze ścinaniem:

n

wp

n

l

c

t

e









1

5

,

0

0

,

,

,

,

M

y

n

el

Rd

el

n

Ed

n

f

W

M

M















































2

,

,

0

,

,

,

,

1

2

1

Rd

pl

n

Ed

M

y

n

el

Rd

el

n

Ed

n

V

V

f

W

M

M

