STEROWANIE NIEZAWODNOŚCIĄ

PARKU ŚRODKÓW TRANSPORTOWYCH

JÓZEF OKULEWICZ, TADEUSZ SALAMONOWICZ

Politechnika Warszawska

[e-mail]

,

[e-mail]

Streszczenie: W pracy przedstawiono metodę utrzymywania
wymaganej niezawodności środków transportu poprzez stosowanie
nadmiaru obiektów oraz wykonywanie odnów profilaktycznych.
Jako kryterium przyjęto akceptowalny poziom ryzyka uszkodzenia
w czasie realizacji zadań transportowych. Przedstawiono
i zilustrowano przykładem algorytm wyboru elementów do
wymiany profilaktycznej.

Słowa kluczowe: niezawodność, nadmiarowość, odnowa
profilaktyczna

1. WSTĘP
Zadania logistyczne coraz częściej nabierają charakteru

jednorazowych przedsięwzięć będących wynikiem zbiegu rozmaitych
uwarunkowań (wymagań i ograniczeń), połączonych przez logistyka
w jeden łańcuch, tzn. w uporządkowaną sekwencję działań.
Uwzględnienie możliwości uszkodzenia któregoś z elementów
wykonawczych tej sekwencji, na skutek czego mogłaby nie być
zrealizowana założona funkcja, wymaga zaprojektowania systemu
logistycznego z uwzględnieniem zawodności poszczególnych powiązań,
gdyż inaczej zniweczyłoby to często sam pomysł takiego powiązania
działań. Dlatego naturalnym jest wymaganie wysokiej niezawodności
użytkowanych obiektów.

W systemach transportowych wymagania te dotyczą przede

wszystkim środków transportu. Wobec nieuchronności występowania
rozmaitych uszkodzeń, niezbędne jest utrzymywanie odpowiedniego
nadmiaru tych środków, dzięki czemu możliwe jest zastępowanie
uszkodzonych obiektów i kontynuowanie realizacji zadań przewozowych.
Liczba nadmiarowych środków zależy od przewidywanego a zarazem
akceptowalnego prawdopodobieństwa uszkodzenia w okresie realizacji
planowanego zadania. W celu minimalizowania liczebności nadmiaru
należy z jednej strony stosować obiekty o wysokiej niezawodności

a z drugiej w procesie eksploatacji utrzymywać ich niezawodność na
możliwie wysokim poziomie.

Załóżmy, że do realizacji zadań przewozowych niezbędnych jest

n obiektów. Jeżeli cały park liczy n obiektów to można przyjąć, że
struktura niezawodnościowa tego parku jest szeregowa. Nakłada to duże
wymagania na niezawodność każdego obiektu, co nie zawsze jest
możliwe do spełnienia. Wówczas aby utrzymać niezawodność parku na
wymaganym poziomie można wprowadzić do parku nadmiarowe obiekty.
Dodanie do parku k obiektów nadmiarowych powoduje, że strukturę
niezawodnościową parku można rozpatrywać jako strukturę progową,
w tym przypadku „n z n+k”.

2. RODZAJE NADMIARÓW
Nadmiarowe obiekty mogą pełnić rolę rezerwy zimnej

(nieobciążonej), czyli oczekują biernie na uszkodzenie któregoś
z obiektów, bądź rezerwy gorącej (obciążonej) zwiększając przejściowo
wydajność całego parku do czasu uszkodzenia się któregoś z obiektów.
Model niezawodnościowy parku zależy wiec od sposobu funkcjonowania
obiektów nadmiarowych.

W przypadku struktury „n z n+1” z rezerwą zimną funkcja

niezawodności parku R

n

(t) będzie sumą prawdopodobieństw wystąpienia

następujących sytuacji:

1) do chwili t nie uszkodzi się żaden obiekt spośród n obiektów

tworzących szeregową strukturę niezawodnościową,

2) w dowolnej chwili

τ

< t uszkodzi się jeden spośród n obiektów

i zostanie zastąpiony obiektem rezerwowym, który wraz
z pozostałymi obiektami nie uszkodzi się w przedziale (

τ

, t).

Prawdopodobieństwa wystąpienia powyższych sytuacji wynoszą

odpowiednio:

P

1

= R

n

(t)

(1)

gdzie: R(t) – funkcja niezawodności każdego obiektu,

( ) ( )

∫

=

t

0

n

n

2

d

t

τ,

R

τ

f

P

τ

(2)

gdzie: f

n

(

τ

) –

gęstość prawdopodobieństwa uszkodzenia jednego
spośród n jednakowych obiektów tworzących szeregową
strukturę niezawodnościową,

R

n

(

τ

, t) – prawdopodobieństwo nieuszkodzenia w przedziale (

τ

, t)

parku składającego się z (n-1) obiektów w wieku

τ

i jednego obiektu rezerwowego (nowego).

( )

( )

( )

(

)

τ

t

R

τ

R

t

R

t

τ,

R

1

n

n

−









=

−

(3)

( )

( )

[

]

( ) ( )

τ

f

τ

R

n

τ

R

1

dτ

d

τ

f

1

n

1

n

n

−

−

=

−

=

(4)

( ) ( ) (

)

∫

−

=

−

t

0

1

n

2

dτ

τ

t

R

τ

f

τ

nR

P

(5)

( )

( ) ( )

( ) (

)













−

+

=

+

=

∫

−

t

0

1

n

2

1

n

dτ

τ

t

R

τ

f

n

t

R

t

R

P

P

t

R

(6)

W przypadku struktury „n z n+2” opis analityczny komplikuje się

bardziej gdyż istnieje drugi obiekt rezerwowy. Oznacza to bowiem, że
w utworzonym w chwili

τ

parku składającym się z (n-1) obiektów

w wieku

τ

i jednego obiektu nowego może przed chwilą t uszkodzić się

jeden z obiektów i być zastąpiony przez drugi obiekt rezerwowy.

Gęstość prawdopodobieństwa uszkodzenia parku o strukturze

„n z n+1” z rezerwą zimną wyraża się zależnością:

( )

( )

[

]

(

)

( ) ( ) ( ) (

)

∫

−

−

=

−

=

−

+

t

0

2

n

n
n

1

n

dτ

τ

t

R

τ

f

t

f

t

R

1

n

n

t

R

1

dt

d

t

f

(7)

i nie są znane żadne wzory rekurencyjne.

W przypadku parku o strukturze „n z n+k” z rezerwą gorącą możemy

skorzystać z zależności

i

k

n

i

k

n

n

i

k)

(n,n

R)

(1

R

i

k

n

R

−

+

+

=

+

−







 +

=

∑

(8)

oraz wzoru rekurencyjnego

(

)

(

)

(

)

(

)

1

k

n

n,

1

k

n

1,

n

k

n

n,

R

R

1

R

R

R

−

+

−

+

−

+

⋅

−

+

⋅

=

(9)

Złożoność opisu analitycznego mimo uczynionych założeń

upraszczających (tzn. jednakowe obiekty, pominięcie struktury
niezawodnościowej samych obiektów) wskazuje na potrzebę
zastosowania do rozpatrywanych zagadnień symulacji komputerowej.

3. ODNOWY PROFILAKTYCZNE
Poza utrzymywaniem nadmiaru obiektów w parku istotne jest

utrzymywanie wysokiego poziomu niezawodności obiektów technicznych
w procesie ich eksploatacji. Służą temu odnowy profilaktyczne
polegające na uprzedzającej wymianie elementów składowych
zagrożonych uszkodzeniem.

Znana z literatury metoda określania zakresu i terminów odnów

profilaktycznych polega na uwzględnieniu kosztów wymian
uprzedzających i kosztów spowodowanych występującymi
uszkodzeniami [2]. W wyniku stosowania tej metody można uzyskać
minimalne jednostkowe koszty utrzymania obiektów w odpowiednim
stanie niezawodnościowym. Jednak dla skorzystania z tego efektu trzeba
wymieniać poszczególne elementy w różnych odstępach czasu, zwykle
nieskoordynowanych z wykonywaniem zadań, co może niweczyć
korzyści z przeprowadzonej optymalizacji. Dlatego należy rozważyć
możliwość wykonywania wymian profilaktycznych wybranych
elementów obiektów w założonych odstępach czasu, których zakres
określa się na podstawie oceny niezawodności elementów i założonego
poziomu niezawodności całego parku [3].

W przypadku obiektów złożonych uszkodzenie następuje wtedy, gdy

uszkodzi się element tworzący z pozostałymi szeregową strukturę
niezawodnościową. Naprawa zwykle polega na wymianie tego elementu
na nowy. Jednakże wymiana uszkodzonego elementu na nowy nie
spowoduje przywrócenia stanu niezawodnościowego takiego jak przed
uszkodzeniem. Wartość funkcji niezawodności uszkodzonego elementu
była przed uszkodzeniem mniejsza od jedności, a po wymianie jest równa
jedności. W wyniku tego stan obiektu po naprawie jest nieco lepszy niż
tuż przed uszkodzeniem. Nie ma zatem praktycznie możliwości
odtworzenia po naprawie stanu obiektu takiego jaki był tuż przed
uszkodzeniem. Proces naprawiania obiektu poprzez wymiany elementów
składowych jest procesem o skokowej zmianie funkcji niezawodności
w chwili naprawy elementu składowego.

Model analityczny opisujący proces zmian stanu technicznego

obiektu (uszkodzenia i wymiany elementów) jest analogiczny do
przedstawionego powyżej modelu niezawodnościowego parku
z nadmiarowymi obiektami z rezerwą zimną. Wobec złożoności modeli,
w których uwzględnia się dużą liczbę elementów składowych obiektów
potrzebne jest kryterium, które umożliwiłoby stosowanie przyjętej
strategii odnów profilaktycznych w praktyce.

Przy projektowaniu strategii odnów profilaktycznych uwzględnia się

zarówno obiekty jak i ich elementy składowe. Własności elementów są
bardziej przewidywalne niż złożonych z nich obiektów.

Dynamiczne wyznaczanie zakresu odnów profilaktycznych polega na

statystycznej ocenie aktualnego stanu elementów obiektu. W tym celu
potrzebne są dane o rozkładzie prawdopodobieństwa czasu do
uszkodzenia i o jego parametrach oraz o dotychczasowym czasie
eksploatacji (od nowości lub chwili wymiany). Na tej podstawie określa
się zbiór elementów, których wymiana spowoduje, że
prawdopodobieństwo uszkodzenia w okresie planowanego zadania nie
przekroczy założonej wartości.

Dla dowolnej chwili t musi być spełniony warunek:

d

(t)

q

p

≥

(10)

gdzie: d –

okres realizacji zadania,

q

p

(t) – kwantylowa funkcja pozostałego czasu poprawnej pracy,

rzędu p.

Funkcję q

p

(t) definiuje się następująco [1]:

( )

}

{

p

(x)

F

:

x

inf

p

F

(t)

q

t

1

t

p

≥

=

=

−

(11)

gdzie:

0

t

x,

,

R(t)

x)

R(t

(x)

R

(x)

F

1

t

t

≥

+

=

=

−

,

F

t

(x) – dystrybuanta pozostałego czasu poprawnej pracy,

R

t

(x) – warunkowa funkcja niezawodności.

Nie bierze się przy tym pod uwagę faktycznego stanu technicznego

obiektu, gdyż wymagałoby to wyłączenia obiektu z eksploatacji. Kontrola
statystyczna może być dokonana w dowolnej chwili gdyż bazuje na
danych zgromadzonych w sferze informacyjnej systemu zarządzania
eksploatacją środków transportu. Mając dane charakterystyki
niezawodnościowe elementów, czas dotychczasowej pracy
poszczególnych elementów, okres realizacji zadania transportowego
można określić elementy, które wymagają wymiany profilaktycznej aby
prawdopodobieństwo wykonania tego zadania nie było mniejsze od
zadanej wartości. Można też wyznaczyć prawdopodobieństwo
uszkodzenia w okresie realizacji zadania zarówno w przypadku
wykonania tych wymian jak i bez ich wykonania. Dodatkowo ocena może
dotyczyć całego parku obiektów wyznaczonego do realizacji zadania
transportowego.

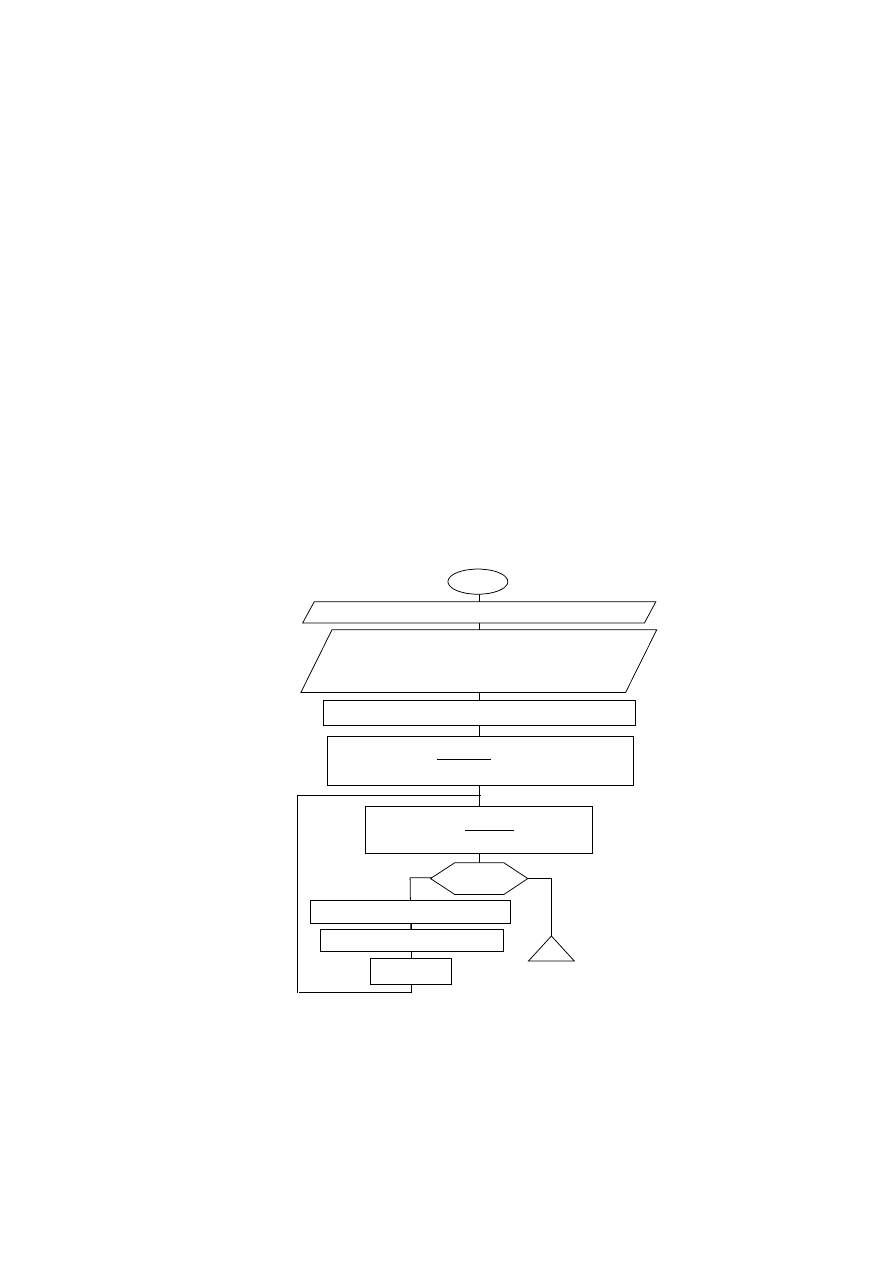
4. ALGORYTM WYBORU ELEMENTÓW DO WYMIANY
Odnowę profilaktyczną elementów wykonuje się jeśli obliczona dla

całego zbioru obiektów wartość funkcji (11)

zadanego rzędu jest mniejsza

od czasu trwania planowanego zadania dla tego zbioru obiektów. W celu
wytypowania zbioru elementów do wymiany oblicza się aktualną wartość
funkcji niezawodności wszystkich elementów z uwzględnieniem czasu
dotychczasowego działania każdego z nich. Następnie oblicza się kwantyl
zadanego rzędu dla rozkładu pozostałego czasu poprawnej pracy każdego
elementu. Elementy porządkuje się wg rosnącej wartości kwantyla.

Do wymiany typuje się kolejno elementy poczynając od elementu

o najmniejszej wartości kwantyla do czasu aż kwantyl całego parku
obiektów obliczony z uwzględnieniem wymiany na nowe wytypowanych
elementów będzie nie mniejszy od czasu planowanego zdania (algorytm
na rys.1). Wymiana wyznaczonych w ten sposób elementów zapewnia
zadane prawdopodobieństwo nieuszkodzenia obiektu podczas
wykonywania zadania transportowego.

p = rząd kwantyla rozkładu

prawdopodobieństwa czasu do uszkodzenia

obiektu w przedziale

od t do t + d

R

i

(t) = niezawodność i-tego elementu, i= 1, … N













−

≤

+

=

p)

(1

(t)

R

x)

(t

R

:

x

inf

(t)

q

i

i

pi

, i= 1, … N

q

p

(t) < d

d = odstęp czasu pomiędzy kontrolami stanu

start

tak

nie

q

pj

(t) = min {q

pi

(t) , i= 1, … N }

wymiana elementu j-tego

q

pj

=

∞













−

≤

+

=

p)

(1

R(t)

x)

R(t

:

x

inf

(t)

q

p

Rys.1. Algorytm wyboru elementów do wymiany profilaktycznej

Przykład. Do realizacji zadań są niezbędne 3 obiekty. Dopuszczalne

(akceptowalne) prawdopodobieństwo wystąpienia niezdatności parku
wynosi p = 0,1. Obiekt składa się z 3 elementów o jednakowym
rozkładzie prawdopodobieństwa czasu do uszkodzenia: rozkład Weibulla

α

= 2,5,

β

= 50.

Możliwe są następujące strategie użytkowania:

1. użytkuje się 3 obiekty (park bez nadmiaru),
2. użytkuje się 4 obiekty (jeden obiekt nadmiarowy, rezerwa

gorąca),

3. użytkuje się 5 obiektów (dwa obiekty nadmiarowe, rezerwa

gorąca).

W każdym przypadku wymaganą niezawodność utrzymuje się

poprzez wymiany profilaktyczne elementów W rozwiązaniu zastosowano
na poziomie obiektów model niezawodnościowy struktury „n z n+k”
z rezerwą zimną, a na poziomie parku – z rezerwą gorącą. Wyniki
symulacji dla czasu 500:

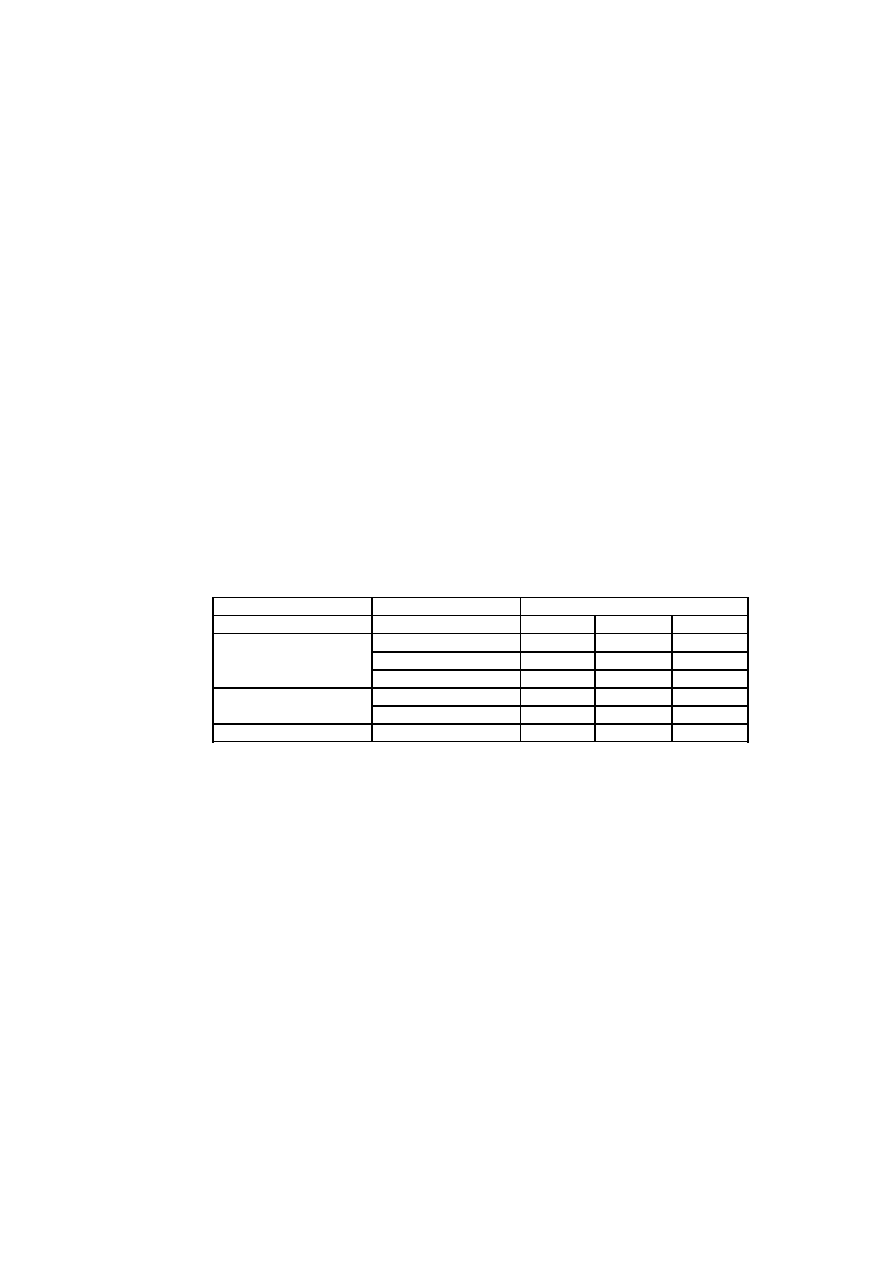
Tab. 1. Wyniki eksperymentu symulacyjnego

Wariant

Kontrole statystyczne

3 z 3

3 z 4

3 z 5

Średnia liczba
uszkodzeń

co 5

9,9

17,4

24,6

co 3

14,6

24,7

34,8

bez profilaktyki

101,2

116,2

130,9

Średnia liczba wymian
profilaktycznych

co 5

397,6

351,8

331,5

co 3

281,3

249,1

233,8

Kwantyl rzędu 0,1

8,4

15,2

19,5

Z przeprowadzonego eksperymentu symulacyjnego można

sformułować następujące wnioski:

1) poprzez zastosowanie kontroli statystycznej można uzyskać

znaczące obniżenie liczby przypadkowych uszkodzeń elementów
w porównaniu z użytkowaniem bez kontroli statystycznych,

2) im krótszy jest odstęp pomiędzy kontrolami tym większa jest

dopuszczalna liczba uszkodzeń na wymaganym poziomie
niezawodności,

3) dodanie nadmiarowego obiektu powoduje zwiększenie liczby

uszkodzeń elementów z czym wiąże się zmniejszenie liczby
wymian profilaktycznych.

5. ZAKOŃCZENIE
Na podstawie porównania strategii użytkowania można przyjąć, że

stosowanie nadmiarowych obiektów w parku umożliwia uzyskanie
wymaganego poziomu niezawodności przy użyciu mniejszej liczby
elementów wymienianych profilaktycznie.

Prezentowana metoda wyznaczania zakresu wymian profilaktycznych

na podstawie własności niezawodnościowych elementów składowych
eksploatowanych obiektów umożliwia dobranie parametrów wymian dla
zadanych parametrów niezawodności obiektów.

Analiza niezawodności w aspekcie wymian profilaktycznych może

być wykonywana w odniesieniu do elementów o krytycznym znaczeniu
dla realizowanego zadania. Można ją wykonać dla dowolnego zbioru
obiektów, jakie razem będą wykorzystywane do realizacji zadania.

RELIABILITY CONTROL

OF MEANS OF TRANSPORT

A method of means of transport maintenance with
a requisite reliability is presented. Results are achieved
by redundancy of objects in a fleet and by preventive
replacement of objects’ elements. The acceptable level
of failure risk during realisation of transport tasks was
taken in the developed algorithm as a criterion of
choosing the elements to replacement.

LITERATURA

[1] Joe H., Proschan F.: Percentile residual life functions. Operations

Research, vol. 32, 3; str. 668-679, 1983.

[2] Karpiński J., Firkowicz Sz.: Zasady profilaktyki obiektów

technicznych. PWN, Warszawa 1981.

[3] Okulewicz J., Salamonowicz T.: Porównanie wybranych strategii

odnów profilaktycznych. Materiały XXXIV Zimowej Szkoły
Niezawodności, str. 218-227, Szczyrk 2006.

[4] Salamonowicz T.: Model niepełnej odnowy przy naprawach

wymuszonych i profilaktycznych. Materiały XXXIII Zimowej Szkoły
Niezawodności, str. 464-469, Szczyrk 2005.