część 2
1
Człowiek- najlepsza inwestycja
Projekt współfinansowany przez Unię Europejską
w ram ach Europejskiego Funduszu Społecznego
Eksploatacja urządzeń
mechatronicznych
Część 2: Modele matematyczne
niezawodności wyrobów
Matematyczne ujecie
niezawodności
Charakterystyki funkcyjne
Charakterystyki liczbowe
Charakterystyki funkcyjne
Funkcja niezawodności wyrobu
Dystrybuanta rozkładu zmiennej losowej t
Gęstość prawdopodobieństwa zmiennej losowej t
Intensywność uszkodzeń wyrobu
Funkcja wiodąca
Charakterystyki funkcyjne
Charakterystyki liczbowe
Niezawodność a prawdopodobieństwo
Niezawodność obiektu = prawdopodobieństwo
spełnienia przez obiekt
stawianych mu
wymagań
Spełnienie wymagań = „sukces”
Niezawodność obiektu = prawdopodobieństwo
sukcesu
Niezawodność a prawdopodobieństwo
„sukces” = obiekt sprawny w przedziale (t
1
;t
2
)
Miarą przedziału (t
1
;t
2
) może być:
• Czas,
• Ilość wykonanej pracy,
• Liczba wykonywanych czynności,
• Długość przebytej drogi, itp.
Niezawodność obiektu = prawdopodobieństwo,
ż
e obiekt będzie sprawny
w przedziale (t
1
;t
2
)
Matematyczne ujecie
niezawodności
Niezawodność jest mierzalną własnością obiektu
Miarą niezawodności jest prawdopodobieństwo zajścia
zdarzenia (losowego) polegającego na tym, że obiekt
będzie funkcjonował poprawnie przez wymagany czas w
określonych warunkach
Prawdopodobieństwo to jest nazywane
funkcją
niezawodności wyrobu
część 2
2
T – zmienna losowa opisująca czas do
uszkodzenia się wyrobu,
tzw.
czas zdatności
lub
trwałość
R(t) – funkcyjna charakterystyka niezawodności
tzw.
niezawodność
Funkcja niezawodności R(t)
( )
{
}
t
T
P
t
R
≥
=
Funkcja niezawodności wyrobu
( )
{
}
t
T
P
t
R
≥
=
( )
t
R
0
,
1
0
t
czas
Funkcja zawodności F(t)
prawdopodobieństwo uszkodzenia
( )
{
}
( )
t
R
t
T
P
t
F
−
=
<
=
1
0
,
1
0
t
czas
( )
t
F
F(t)
R(t)
Gęstość prawdopodobieństwa
Często stosowana w matematycznym
opisie czasu funkcjonowania do
uszkodzenia się wyrobu
( )
( )
dt
t
dR
dt
t
dF
t
f
)
(
−
=
=
Intensywność uszkodzeń
Funkcja ryzyka
Korzystając z wzoru Taylora mamy przybliżenie:
( )
[
]
( )
t
R
t
f
t
R
dt
d
t
)
(
)
(
ln
=
−
=
λ
( )
t
t
t
R
t
R
t
f
∆
∆
+
−
≈
)
(
)
(
Stąd:
( )
t
t
R
t
t
R
t
R
t
∆
∆
+
−
≈
)
(
)
(
)
(
λ
Niezawodność a intensywność uszkodzeń
R(0) – początkowa niezawodność wyrobu
(w chwili rozpoczęcia użytkowania)
Funkcję niezawodności wyrobu możemy
uzależnić od funkcji intensywności uszkodzeń
( )
( )
( )
∫
−
=
t
dx
x
R
t
R
0
exp
0
λ
część 2
3
Przebieg funkcji intensywności
uszkodzeń
I.
Okres starzenia wstępnego lub docierania
II.
Okres tzw. normalnego użytkowania
III.
Okres tzw. katastroficznego zużycia
0
t
( )
t
λ
I
II
III
Przebieg funkcji intensywności
uszkodzeń cd.
I.
Okres starzenia wstępnego lub docierania
Ujawniają się wady produkcyjne nie wykryte przez
kontrolę odbiorczą
Okres dużej i malejącej intensywności uszkodzeń
II.
Okres tzw. normalnego użytkowania
Intensywność uszkodzeń w przybliżeniu stała co do
wartości
III.
Okres tzw. katastroficznego zużycia
Uszkadzają się pozostałe egzemplarze wyrobu
Wykładnicze prawo
niezawodności
Okres I jest zazwyczaj obejmowany gwarancją i w
rozważaniach dotyczących niezawodności bywa
pomijany
W takim przypadku czas do uszkodzenia się wyrobu ma
rozkład wykładniczy
Jest to tzw.
wykładnicze prawo niezawodności zwane
wzorem Wienera
( )
1
0
=
R
( )
(
)
t
t
R
λ
−
= exp
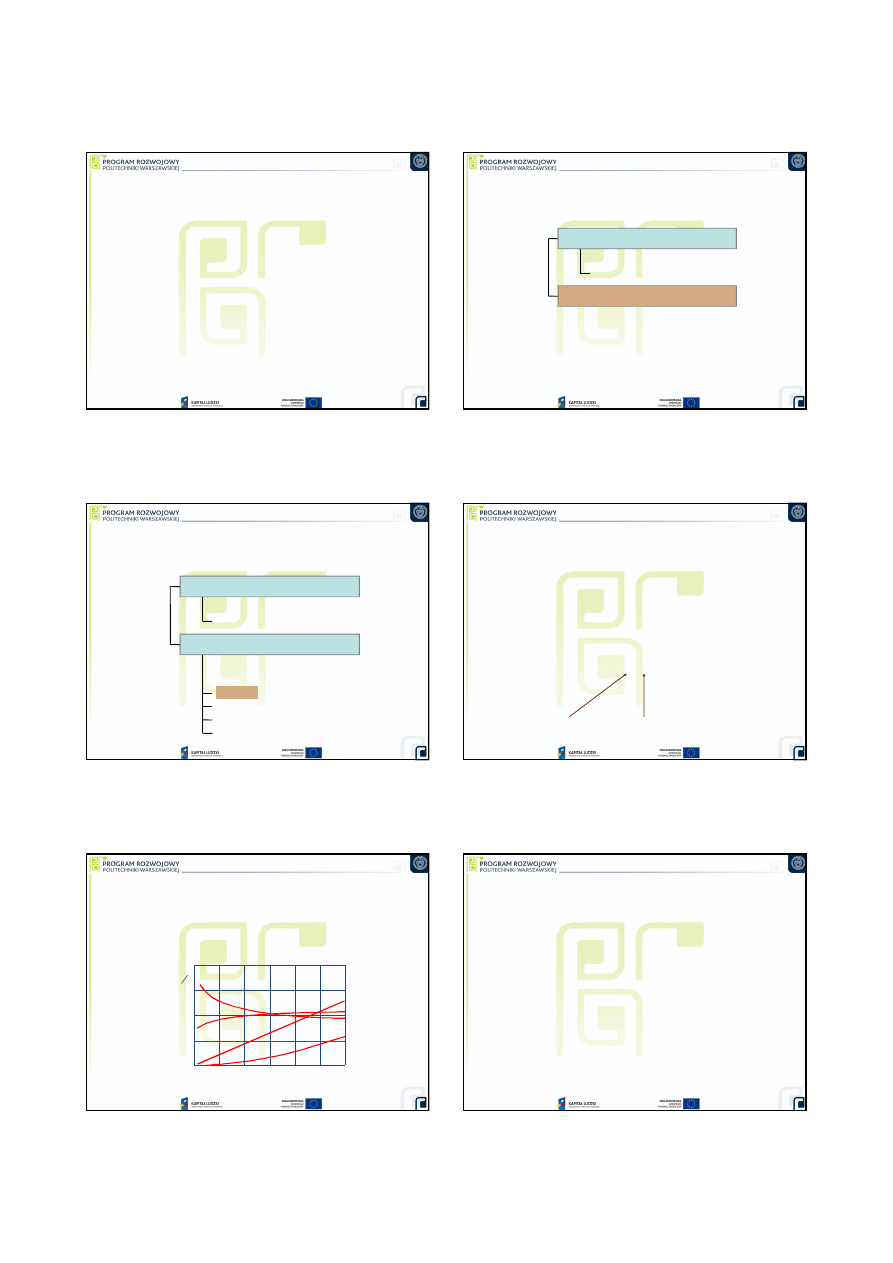
Intensywność uszkodzeń -
przykład
0
10
20
30
40
50
60
70
80
Funkcja wiodąca
Informuje o wyczerpaniu się „zapasu
niezawodności” obiektu
( )
[
]
( )
0
)
(
ln
0
≥
=
−
=
Λ
∫
t
du
u
t
R
t
t
λ
Funkcja wiodąca
( )
[
]
( )
du
u
t
R
t
t
∫
=
−
=
Λ
0
)
(
ln
λ
0
t
czas
( )
t
Λ
część 2
4
Charakterystyki liczbowe
Funkcja niezawodności wyrobu
Dystrybuanta rozkładu zmiennej losowej t
Gęstość prawdopodobieństwa zmiennej losowej t
Intensywność uszkodzeń wyrobu
Funkcja wiodąca
Charakterystyki funkcyjne
Charakterystyki liczbowe
Charakterystyki liczbowe
Funkcja niezawodności wyrobu
Dystrybuanta rozkładu zmiennej losowej t
Gęstość prawdopodobieństwa zmiennej losowej t
Intensywność uszkodzeń wyrobu
Funkcja wiodąca
Charakterystyki funkcyjne
Oczekiwany czas zdatności
Wariancja czasu zdatności
Ś
rednia intensywność uszkodzeń
Resurs gamma-procentowy
Charakterystyki liczbowe
Oczekiwany czas zdatności
Wartość oczekiwana czasu zdatności
lub
( )
dt
t
tf
ET
∫
∞
=
0
( )
∫
∞
=
0
dt
t
R
ET
Oczekiwany czas zdatności
( )
t
R
0
,
1
0
t
czas
ET
Wariancja czasu zdatności
• Wariancja czasu zdatności
• Odchylenie standardowe
Odchylenie standardowe charakteryzuje rozrzut
wartości czasu T do uszkodzenia wokół jej
wartości oczekiwanej ET
2
2
)
(ET
ET
VT
−
=
VT
T
=
σ
Opis rozkładu zmiennej losowej przy
pomocy kwantyli
p
- poziom ( liczba z przedziału [0, 1] )
t
p
- kwantyl na poziomie p
Kwantyl t
p
jest rozwiązaniem równania F(t)=p
Rozkład zmiennej losowej można w przybliżeniu opisać podając pewna
liczbę kwantyli.
część 2
5
Kwantyl rzędu p
• Kwantyl rzędu p czasu zdatności jest to
pierwiastek t
p
równania:
F(t
p
) =p
• p=0,5 mediana
• p=0,25 kwantyl dolny
• p=0,75 kwantyl górny
Ś
rednia intensywność
uszkodzeń
( )
( )
du
u
t
t
t
ś
r
∫
=
0
1
λ
λ
Resurs gamma-procentowy
Zasób poprawnego funkcjonowania wyrobu przez czas
w którym ulegnie uszkodzeniu γ% egzemplarzy
Rozpatruje się zasoby 95%, 90%, 75% i 50% tzn. czasy
w których uszkodzi się mniej niż odpowiednio 5%, 10%,
25% i 50% wyrobów
( )
%
100
γ
γ
=
t
R
γ
t
Człowiek- najlepsza inwestycja
Projekt współfinansowany przez Unię Europejską
w ram ach Europejskiego Funduszu Społecznego
Eksploatacja urządzeń
mechatronicznych
Rozkłady czasu zdatności
Rozkłady w niezawodności
Rozkłady o jednym parametrze
Rozkłady dwuparametrowe
Rozkłady w niezawodności
wykładniczy
Rozkłady o jednym parametrze
Rozkłady dwuparametrowe

część 2
6
Rozkład wykładniczy
Zależy tylko od jednego parametru, którym jest
stała intensywność uszkodzeń
Za jej pomocą można wyrazić postacie
charakterystyk funkcyjnych oraz liczbowych
( )
const
t
=
=
λ
λ
Rozkład wykładniczy
Charakterystyki funkcyjne:
( )
t
t
e
t
f
e
t
F
e
t
R
t
t
t
λ
λ
λ
λ
λ
=
Λ
=
−
=
=
−
−
−
)
(
)
(
1
)
(
Rozkład wykładniczy
Charakterystyki liczbowe:
λ
λ
λ
)
1
ln(
2
1
p
t
oraz
VT
ET
p
−
−
=
=
=
−
−
Charakterystyka rozkładu
wykładniczego
Stała intensywność uszkodzeń
Tzw. brak pamięci
Przewidywany czas zdatności obiektu użytkowego przez
dowolnie długi czas, jeśli tylko obiekt się w tym czasie nie
uszkodził, jest taki sam jak czas zdatności nowego obiektu
Uwzględnia przypadkowe uszkodzenia pojawiające się
ze stałym natężeniem
Nie uwzględnia zjawisk o charakterze zmęczenia
Powody szerokiego stosowania
1) Prostota obliczeń przy wystarczającej dokładności
2) Istnienie poważnej grupy obiektów, których czas
zdatności ma rozkład wykładniczy lub nieistotnie
różniący się od wykładniczego
3) Możliwość zastosowania informacji o rozkładzie czasu
zdatności elementu do określenia stanu systemu na
podstawie procesów losowych Markowa
Zadanie 1
•
Ustalono, że czas życia żarówek w rzutniku komputerowym ma
rozkład wykładniczy.
•
Zaobserwowano, że na 200 pracujących żarówek 30 uszkodziło się
w ciągu 800h.
•
Obliczyć oczekiwany czas zdatności.
•
Obliczyć jaka część żarówek zostanie uszkodzona w czasie 1000h.
•
Obliczyć jaka część żarówek zostanie uszkodzona w przedziale
czasowym od 1000h do 2000h
P1.3
część 2
7
Zadanie 2
•
Zaobserwowano, że średni czas użytkowania pomp głębinowych
pewnego typu wynosi 12 lat.
•
Czas zdatności tego typu pomp ma rozkład wykładniczy.
•
Ocenić niezawodność pomp w ciągu 5 lat użytkowania.
•
W jakim okresie czasu osiągniemy 90% zapas zdatności pomp?
P1.4
Rozkłady w niezawodności
wykładniczy
Rozkłady o jednym parametrze
Rozkłady dwuparametrowe
Rozkłady w niezawodności
wykładniczy
Rozkłady o jednym parametrze
Weibulla
gamma
Rayleigha
normalny
Rozkłady dwuparametrowe
Rozkład Weibulla
( )
1
−
=
α
αλ
λ
t
t
0
,
0
,
>
>
t
λ
α
Parametr kształtu
Parametr skali
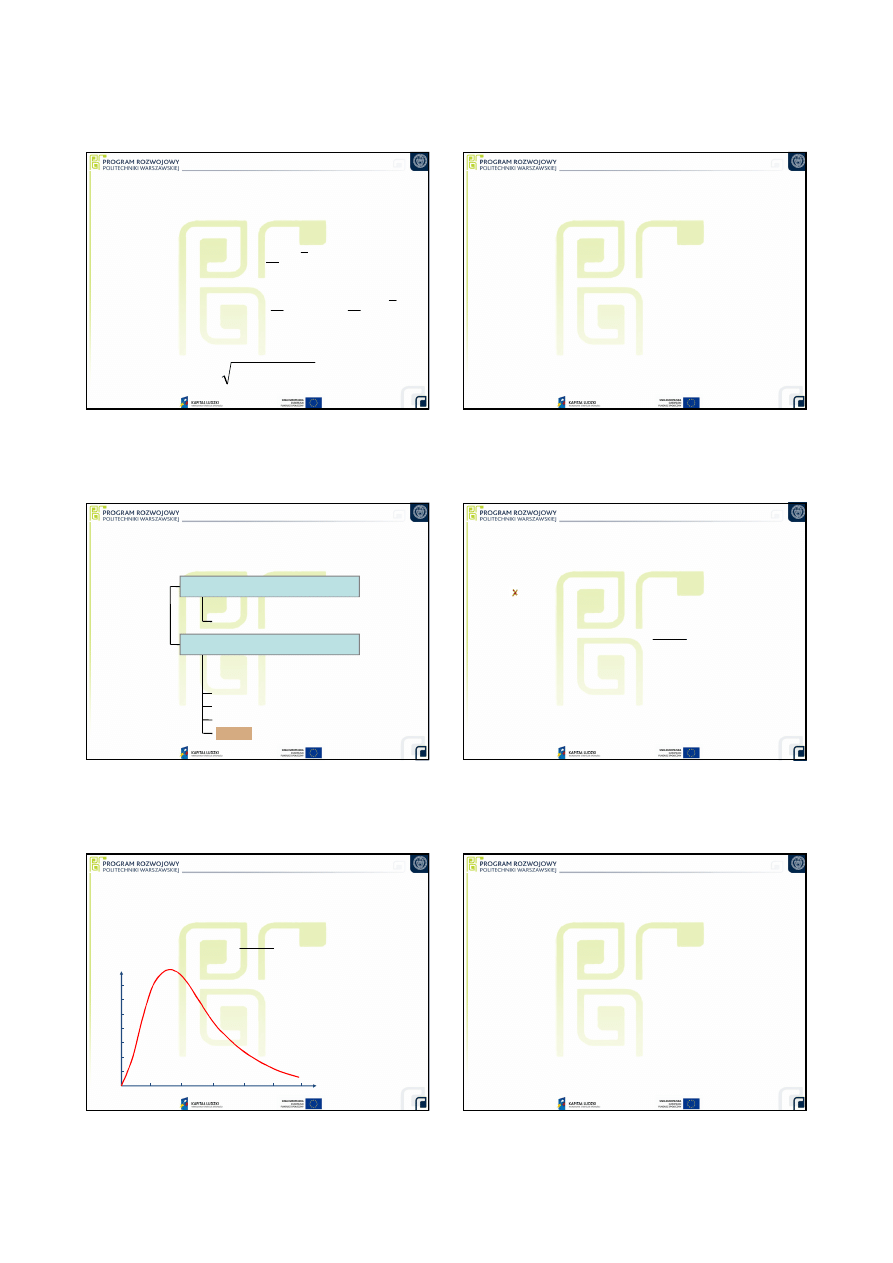
Rozkład Weibulla
( )
3
10
×
t
λ
[ ]
h
1
[ ]
h
t
3
2
1
0
200
400
600
800
1000
1
<
α
)
(
1
y
wykłykładn
=
α
2
>
α
)
(
2 Rayleigha
=
α
2
1
<
<
α
Rozkład Weibulla
Charakterystyki funkcyjne:
( )
α
λ
α
λ
λ
λ
αλ
α
α
α
t
t
e
t
t
f
e
t
F
e
t
R
t
t
t
=
Λ
=
−
=
=
−
−
−
−
)
(
)
(
1
)
(
1
część 2
8
Rozkład Weibulla
Charakterystyki liczbowe:
(
)
α
α
α
λ
λ
α
α
λ
α
p
t
oraz
VT
ET
p
−
−
=
+
Γ
−
+
Γ
=
+
Γ
=
−
−
−
1
ln
1
1
2
1
1
1
1
2
2
1
Zadanie 3
•
Czas pracy narzędzia jest zmienną losową o rozkładzie Rayleigha z
parametrem γ=2,5*10
-3
.Osiągnięcie przez narzędzie stanu
granicznego jest dopuszczalne lecz pociąga straty.
•
Należy ustalić czas pracy narzędzia aby ryzyko osiągnięcia stanu
granicznego było mniejsze niż 0,99.
P1.5
Rozkłady w niezawodności
wykładniczy
Rozkłady o jednym parametrze
Weibulla
gamma
Rayleigha
normalny
Rozkłady dwuparametrowe
Rozkład gamma
Rozkład gamma o
parametrach (
α
,
λ
) ma
gęstość:
gdzie:
oraz
( )
( )
(
)
t
t
t
f
λ
α
λ
α
α
−
Γ
=
−
exp
1
0
≥
t
0
,
>
λ
α
( )
∫
∞
−
−
=
Γ
0
1
du
u
e
u
α
α
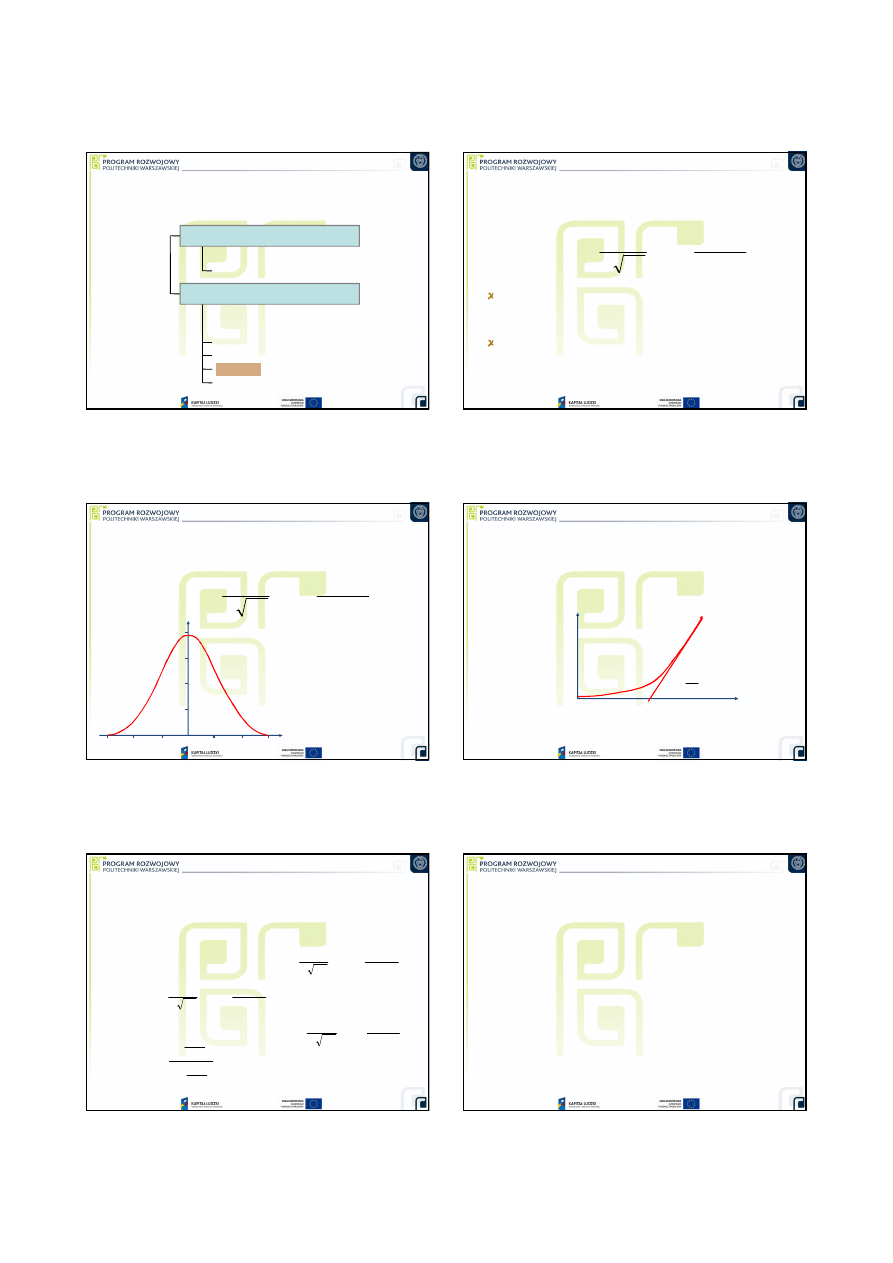
Rozkład gamma
( )
( )
(
)
t
t
t
f
λ
α
λ
α
α
−
Γ
=
−
exp
1
0
≥
t
0
,
>
λ
α
25
,
0
5
,
0
75
,
0
0
,
1
25
,
1
5
,
1
75
,
1
5
,
2
5
5
,
7
10
5
,
12
15
Rozkład gamma
Charakterystyki liczbowe:
2
1
−
−
=
=
αλ
αλ
VT
ET
część 2
9
Rozkłady w niezawodności
wykładniczy
Rozkłady o jednym parametrze
Weibulla
gamma
Rayleigha
normalny
Rozkłady dwuparametrowe
Rozkład normalny
Dotychczasowe rozkłady uwzględniały jedynie warunek
R(0)=1
Gdy prawdopodobieństwa P(T<0) nie można zaniedbać,
rozkład normalny daje możliwość stosowania rozkładu
uciętego, gdy µ<3σ
( )
(
)
−
−
=
2
2
2
exp
2
1
σ
µ
π
σ
t
t
f
Rozkład normalny
( )
(
)
−
−
=
2
2
2
exp
2
1
σ
µ
π
σ
t
t
f
1
,
0
2
,
0
3
,
0
4
,
0
1
2
3
1
−
2
−
3
−
Intensywność uszkodzeń
rozkładu normalnego
t
λ
ET
( )
t
λ
(
)
µ
σ
λ
−
=
t
2
1
Rozkład normalny
(
)
dx
x
t
F
t
∫
∞
−
−
−
=
2
2
2
exp
2
1
)
(
σ
µ
π
σ
Charakterystyki funkcyjne:
(
)
dx
x
t
R
t
∫
∞
−
−
=
2
2
2
exp
2
1
)
(
σ
µ
π
σ
( )
(
)
−
−
=
2
2
2
exp
2
1
σ
µ
π
σ
t
t
f
( )
−
−
=
σ
µ
σ
σ
µ
λ
t
R
t
f
t
Rozkład normalny
Charakterystyki liczbowe:
2
σ
µ
=
=
VT
ET
część 2
10
Zadanie 4
•
Czas zdatności diod laserowych jest zmienną losową o rozkładzie
normalnym. Badaniu poddano 10 losowo wybranych laserów.
Zaobserwowano następujące realizacje czasu życia t[h]:1020; 990;
1030; 970; 1010; 1000; 990; 1000; 1010; 980.
•
Należy oszacować intensywność uszkodzeń dla t=2000h
P4
Rozkłady w niezawodności
wykładniczy
Rozkłady o jednym parametrze
Weibulla
gamma
Rayleigha
normalny
Rozkłady dwuparametrowe
potęgowy
Rozkład potęgowy
Wszystkie dotychczas omówione rozkłady czasy zdatności dobrze
przedstawiają intensywność uszkodzeń w jednym bądź dwóch
okresach użytkowych
Rozkład potęgowy najlepiej przybliża cały rzeczywisty przebieg
intensywności uszkodzeń
=
1
0
)
(
α
b
t
t
F
Dla t 0
Dla 0< t b; α
α
α
α>0, b>0
Dla t>b
≤
≤
Rozkład potęgowy
Charakterystyki funkcyjne:
( )
(
)
α
α
α
α
α
α
α
λ
α
t
b
t
t
t
b
t
f
b
t
t
R
−
=
=
−
=
−
−
1
1
)
(
)
(
/
1
Rozkład potęgowy
Charakterystyki liczbowe:
(
) (
)
2
1
1
2
2
+
+
=
+
=
α
α
α
α
α
b
VT
b
ET
Zadanie 5
•
Czas zdatności pewnego urządzenia jest zmienną losową o
rozkładzie potęgowym z parametrami: α=0,2 i b=100h.
•
Należy znaleźć charakterystyki funkcyjne i liczbowe czasu
zdatności dla t z przedziału [0,100)
P1.70

część 2
11
Zadanie 6
•
Czas zdatności pewnego urządzenia jest zmienną losową o
rozkładzie potęgowym z parametrami: α=0,7 i b=5000h.
•
Należy wyznaczyć intensywność uszkodzeń i podać jej
wartości dla t = 100, 200, 500, 1000, 2000, 3000, 4000, 4500 h.
•
Naszkicować wykres intensywności uszkodzeń
P1.71
Wyszukiwarka
Podobne podstrony:
modele matematyczne opory sedymentacja
Modele matematyczne ukladow reg Nieznany
Pytania na kolokwium cz 2 trudności w matematyce
pr kl IV ul zwykle, MATEMATYKA klasa 4
NOTATKA - Rozwijanie uzdolnień matematycznych w klasach początkowych cz I , edukacja matematyczna z
Modele matematyczne układów elementarnych mod mat
funkcje cz.3, Liceum, Matematyka
karta modele mat.stacj, gik, gik, I sem, modele matematyczne w badaniu przemieszczen
Podstawowe modele matematyczne stosowane w projektowaniu
05 Modele matematyczne charakterys
Statystyka w zadaniach cz.2 Statystyka matematyczna
sprawdzian 3 (gr. I cz.2), kl.1, matematyka
I. Modele matematyczne w ekonomii, ● STUDIA EKONOMICZNO-MENEDŻERSKIE (SGH i UW), ekonomia matematycz
funkcje cz, Liceum, Matematyka
sprawdzian 3 (gr. II cz.1), kl.1, matematyka
funkcje cz.1, Liceum, Matematyka
sprawdzian 3 (gr. I cz.1), kl.1, matematyka
więcej podobnych podstron