1

5. Modele matematyczne charakterystyk przepływowych oporów

pneumatycznych

Jak wiadomo, w zależności od warunków, przepływ płynu w przewodzie może mieć
charakter laminarny (uwarstwiony) lub turbulentny (burzliwy).
W przypadku przepływu laminarnego zależność strumienia objętości od parametrów
przepływu określa wzór Hagena – Poiseuille’a (dla kapilary o przekroju kołowym)

4

128

d

l

p

Q

















gdzie: l – długość kapilary,

d

– średnica kapilary,



- lepkość dynamiczna płynącego

czynnika, p



– różnica ciśnień wywołująca przepływ.

(Dla powietrza pod ciśnieniem atmosferycznym i temperaturze pokojowej

s

m

kg









6

10

19



,

dla cieczy układów hydraulicznych

s

m

kg









3

10

24



)

Znane są wzory dla oporów o innych przekrojach.
W przypadku przepływu laminarnego strumienia objętości powietrza przepływającego przez
opór jest wprost proporcjonalny do różnicy ciśnień wywołującej przepływ. W urządzeniach
pneumatycznych warunki przepływy laminarne mogą wystąpić przy bardzo małych spadkach
ciśnienia rzędu 0,01 bar.

W pneumatyce wysokociśnieniowej praktycznie występują tylko przepływy turbulentne.
W zależności od wartości stosunku ciśnień



1

2

p

p





,

gdzie:

2

p - ciśnienie absolutne za oporem,

1

p - ciśnienie absolutne przed oporem (stosunek

ciśnień



definiuje się dla założonego kierunku przepływu, a więc dla

2

1

p

p



),

rozróżnia się:

- przepływy dokrytyczne, jeżeli

1









kryt

(ruch odbywa się z prędkością mniejszą

od lokalnej prędkości dźwięku),

- przepływy krytyczne, jeżeli

kryt









0

(ruch odbywa się z lokalną prędkością

dźwięku),

- przepływy nadkrytyczne, jeżeli

kryt









0

(ruch odbywa się z prędkością większą

od lokalnej prędkości dźwięku); przepływ nadkrytyczny może wystąpić tylko w
przypadku odpowiednio ukształtowanej dyszy wylotowej – w postaci tzw. dyszy
Lavala.

2

G

0

1





kryt.

P ’’’=const.

1

P ’’=const.

1

P ’=const.

1

Rys. 0. Charakterystyki przepływowe oporu pneumatycznego: G – strumień masy powietrza

płynącego przez opór pneumatyczny,

1

2

p

p





,

2

p - ciśnienie absolutne za oporem,

1

p - ciśnienie absolutne przed oporem (

2

1

p

p



)

Znajomość charakterystyk przepływowych oporów, a właściwie modeli matematycznych tych
charakterystyk, jest podstawą obliczeń związanych z analizą lub projektowaniem układów
pneumatycznych.
Charakterystyką przepływową oporu pneumatycznego nazywa się zależność natężenia
przepływu powietrza płynącego przez opór od czynników wywołujących ten przepływ. W
przypadku oporów pneumatycznych liczba czynników, które mają zauważalny wpływ na
natężenie przepływu jest znaczna (ciśnienia, temperatury czynnika przed i za oporem,
wymiary geometryczne oporu, jego kształt, przebieg procesów cieplnych i inne). Przy tym
wpływ tych czynników na natężenie przepływu może się zmieniać w zależności od charakteru
zjawiska przepływu (przepływ laminarny, turbulentny, dokrytyczny, krytyczny, nadkry-
tyczny). Złożoność zjawisk związanych z przepływami w oporach pneumatycznych powoduje
trudności w sformułowaniu modelu matematycznego dogodnego do praktycznych zastosowań
i jednocześnie wystarczająco dokładnie wyrażającego rzeczywiste właściwości danego oporu.
Poniżej przedstawiono najczęściej wykorzystywane w obliczeniach inżynierskich modele
charakterystyk przepływowych oporów, w których występuje przepływ turbulentny i
uwidoczniono zachodzące pomiędzy nimi relacje. Ograniczono się do modeli, w których
zakłada się stałość parametrów reprezentujących właściwości przepływowe zaworu.

Większość wykorzystywanych do obliczeniach inżynierskich matematycznych modeli
charakterystyk przepływowych oporów pneumatycznych to wzory półempiryczne
wyprowadzone z równania ruchu płynu nielepkiego (Eulera). Całkowanie tego równania przy
założeniu nieściśliwości płynu prowadzi do uzyskania równania Bernoulliego, z którego
wyprowadza się wzór, zwany także wzorem Bernoulliego

)

(

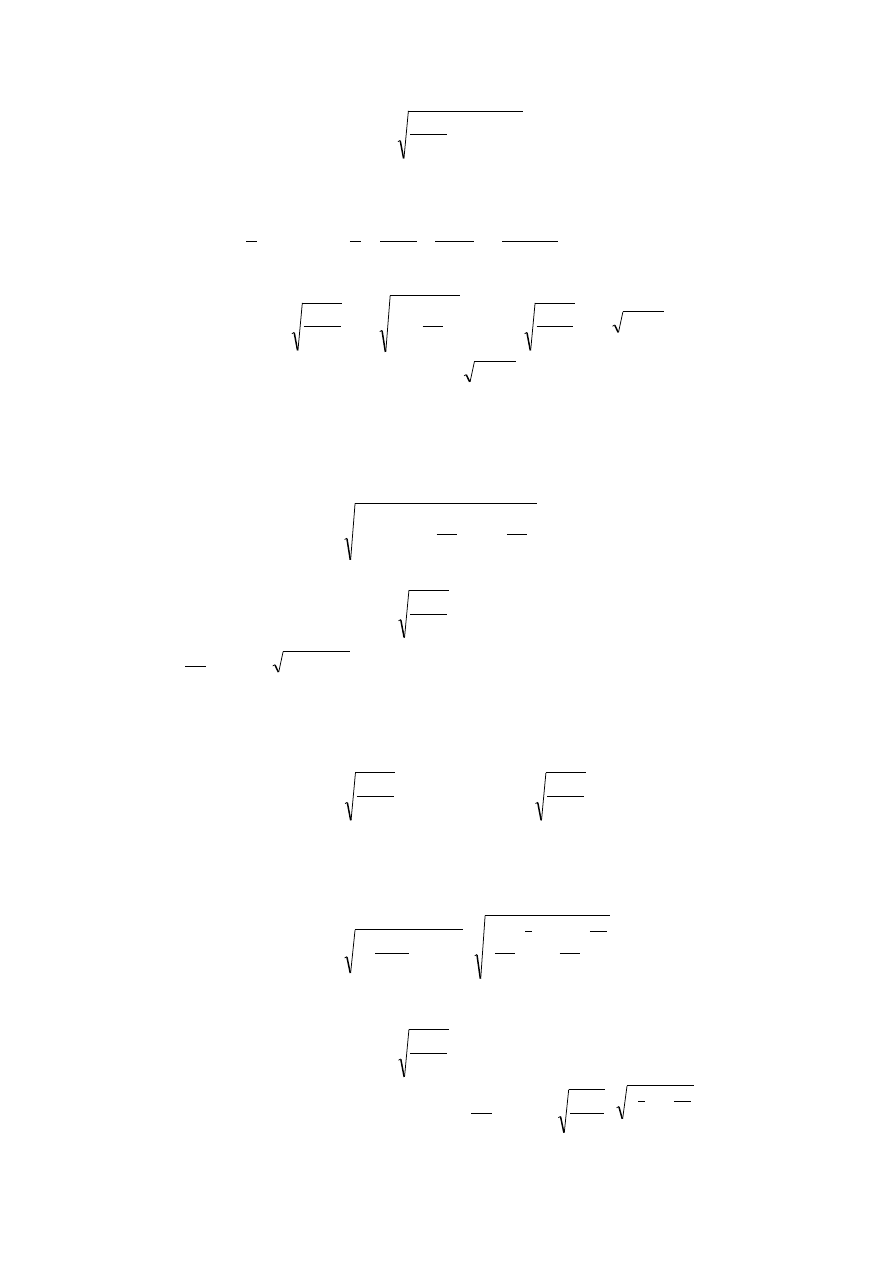
2

2

1

p

p

f

G













,

(1)

wyrażający zależność strumienia masy

G

płynu przepływającego przez opór od warunków

przepływu: ciśnienia przed oporem

1

p , ciśnienia za oporem

2

p (w dalszym ciągu przyjęto, że

oznaczenia

1

p i

2

p reprezentują ciśnienia absolutne statyczne), gęstości płynu



oraz od

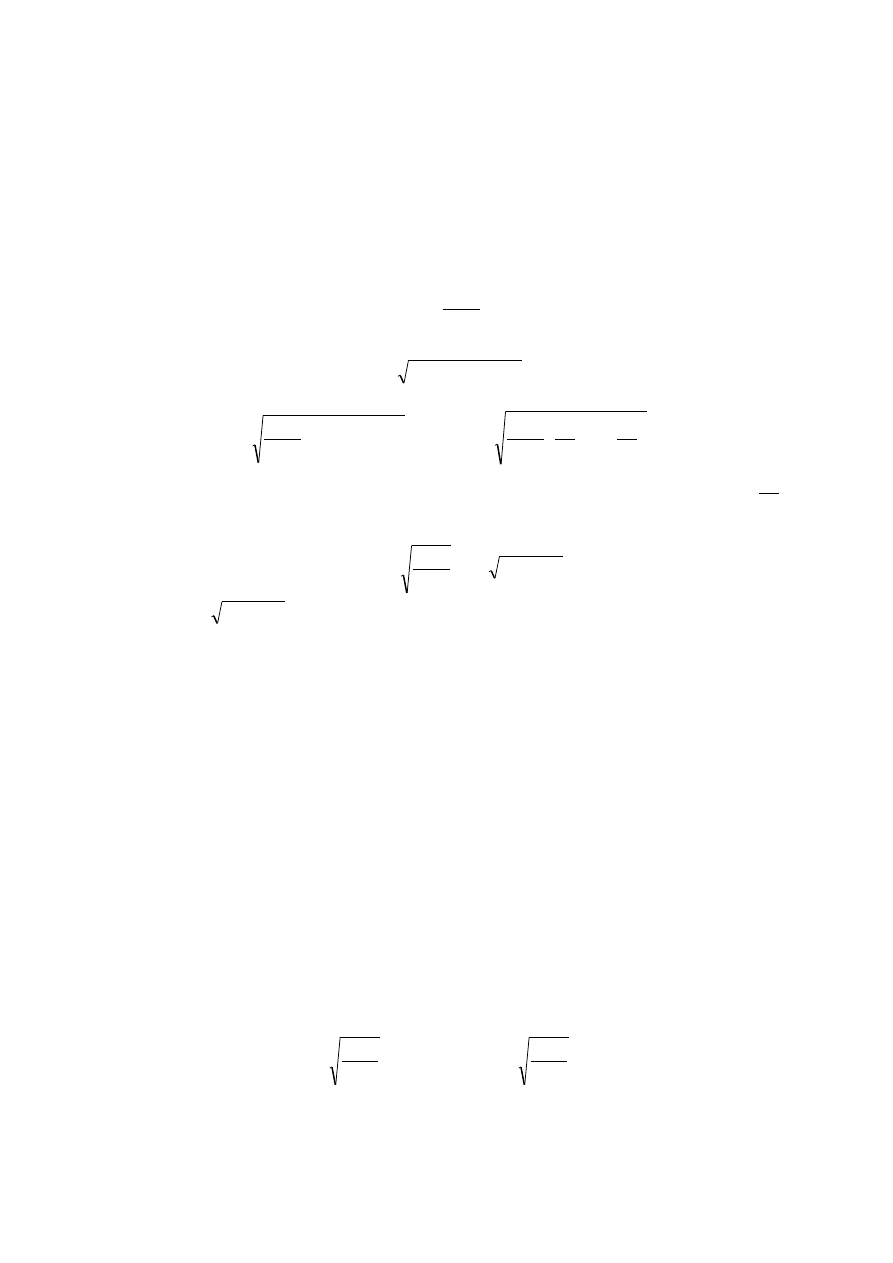
3

parametru reprezentującego właściwości przepływowe oporu - jego powierzchni przepły-
wowej f .
Założenie braku lepkości powoduje zbyt dużą niezgodność modelu i przepływu rzeczywi-
stego, wobec czego wprowadza się dodatkowy parametr korygujący tę niezgodność - współ-
czynnik



, wyznaczany doświadczalnie. Iloczyn

f





, zwany także efektywną powierzchnią

przepływową oporu, można traktować jako jeden parametr określający właściwości
przepływowe oporu. Zakłada się także, że temperatura gazu przy przepływie nie zmienia się i
jest równa temperaturze gazu przed oporem

1

T , a gęstość gazu odpowiada warunkom za

oporem, czyli że

1

2

2

T

R

p











.

Zatem praktyczną postacią wzoru Bernoulliego [2] jest

)

(

2

2

1

2

p

p

f

G

















(2)

lub











































1

2

1

2

1

1

2

1

2

1

1

2

)

(

2

p

p

p

p

T

R

p

f

p

p

p

T

R

f

G





(2’)

W celu analizy właściwości tego modelu wprowadźmy do modelu (2’) zmienną

1

2

p

p





.

Wzór (2’) można więc zapisać w postaci



























1

2

1

1

p

T

R

f

G

,

(2’’)

gdzie funkcja



  















1

nazywana jest funkcją przepływu. Należy zauważyć, że we

wzorach (1) i (2)

1

p oznacza ciśnienie wyższe (przed oporem) niż

2

p (za oporem). Zatem

zmienna



może przyjmować wartości tylko od 0 do 1. Łatwo zauważyć, że

0

)

1

(

)

0

(









oraz, że funkcja

)

(





ma maksimum dla

5

,

0





k





(

k



nazywane jest krytycznym

stosunkiem ciśnień);

5

,

0

)

(



k





.

Zmniejszanie wartość ciśnienia

2

p przy stałej wartości ciśnienia

1

p (zwiększanie spadku

ciśnienia na oporze) winno być związane ze wzrostem wartości strumienia masy. W
przypadku wzorów (2), (2’) i (2’’) zmniejszanie wartości ciśnienia

2

p powoduje wzrost

wartości

G

tylko w zakresie zmian zmiennej



od wartości 1 do

k



. Dalsze zmniejszanie

2

p , co prowadziłoby do zmniejszenia wartości zmiennej



poniżej wartości

k



, powoduje

malenie wartości

G

, co jest niezgodne z rzeczywistością.

Mówi się, że przepływy odpowiadające zakresowi

1









k

to przepływy dokrytyczne; w

zakresie tym natężenie przepływu zależy zarówno od różnicy ciśnień przed i za oporem. W
zakresie

k









0

przepływ jest krytyczny, niezależny od ciśnienia

2

p . W tym zakresie dla

.

1

const

p



, przy zmniejszaniu ciśnienia

2

p wartość

G

pozostaje taka jak dla

1

2

5

,

0

p

p





.

Zatem wzory (2), (2’) i (2’’) stosuje się tylko w przypadku kiedy

1









k

(przepływy

dokrytyczne), natomiast dla

k









0

(przepływy krytyczne) należy wykorzystywać wzór

5

,

0

2

)

(

2

1

1

1

1

























p

T

R

f

p

T

R

f

G

k









(2”’)

Modyfikacją modelu (2) jest tzw. uśredniony wzór Bernoulliego [2]

4





2

2

2

1

1

1

p

p

T

R

f

G















,

(3)

uzyskany z równania (1) przy założeniu, że gęstość



jest wartością średnią gęstości przed

oporem

1



i za oporem

2



(i przy utrzymaniu założenia, że

1

2

T

T



)









2

1

1

2

2

1

1

2

1

2

1

2

1

2

1

p

p

T

R

T

R

p

T

R

p













































Przekształcając wzór (3), otrzymuje się:

2

1

1

2

1

2

1

1

1

2

1

2















































p

T

R

f

p

p

p

T

R

f

G

W tym przypadku funkcja przepływu

2

1

)

(











monotonicznie rośnie od wartości

0

)

1

(





do wartości

1

)

0

(





; można więc przyjąć, że

0



k



. Wzór (3) można więc

stosować w całym zakresie zmienności stosunku



.

Całkowanie równania Eulera z uwzględnieniem ściśliwości płynu wg przemiany izotermi-
cznej prowadzi do modelu przepływu







































2

1

2

1

2

1

1

ln

2

p

p

p

p

p

f

G





(4)

lub w innej postaci

)

(

2

1

1



















p

T

R

f

G

gdzie:

1

2

p

p





,

1

2

ln

)

(















.

Funkcja

)

(





ma maksimum dla

60653

,

0





k





, przy czym

4289

,

0

)

(



k





.

Dla

1









k

(przepływ dokrytyczny) wykorzystuje się model (4), a dla

k









0

(przepływ krytyczny) model

4289

,

0

2

)

(

2

1

1

1

1

























p

T

R

f

p

T

R

f

G

k









(4’)

Całkowanie równania Eulera z uwzględnieniem ściśliwości płynu wg przemiany politro-
powej prowadzi do modelu przepływu zwanego, w przypadku gdy

4

,

1



n

(przemiana

adiabatyczna) wzorem de Saint-Venanta-Wentzela

n

n

n

p

p

p

p

p

n

n

f

G













































1

1

2

2

1

2

1

1

1

2





(5)

lub w innej postaci

 



















1

1

2

p

T

R

f

G

gdzie: n - wykładnik przemiany politropowej,

1

2

p

p





,

 

n

n

n

n

n











1

2

1









.

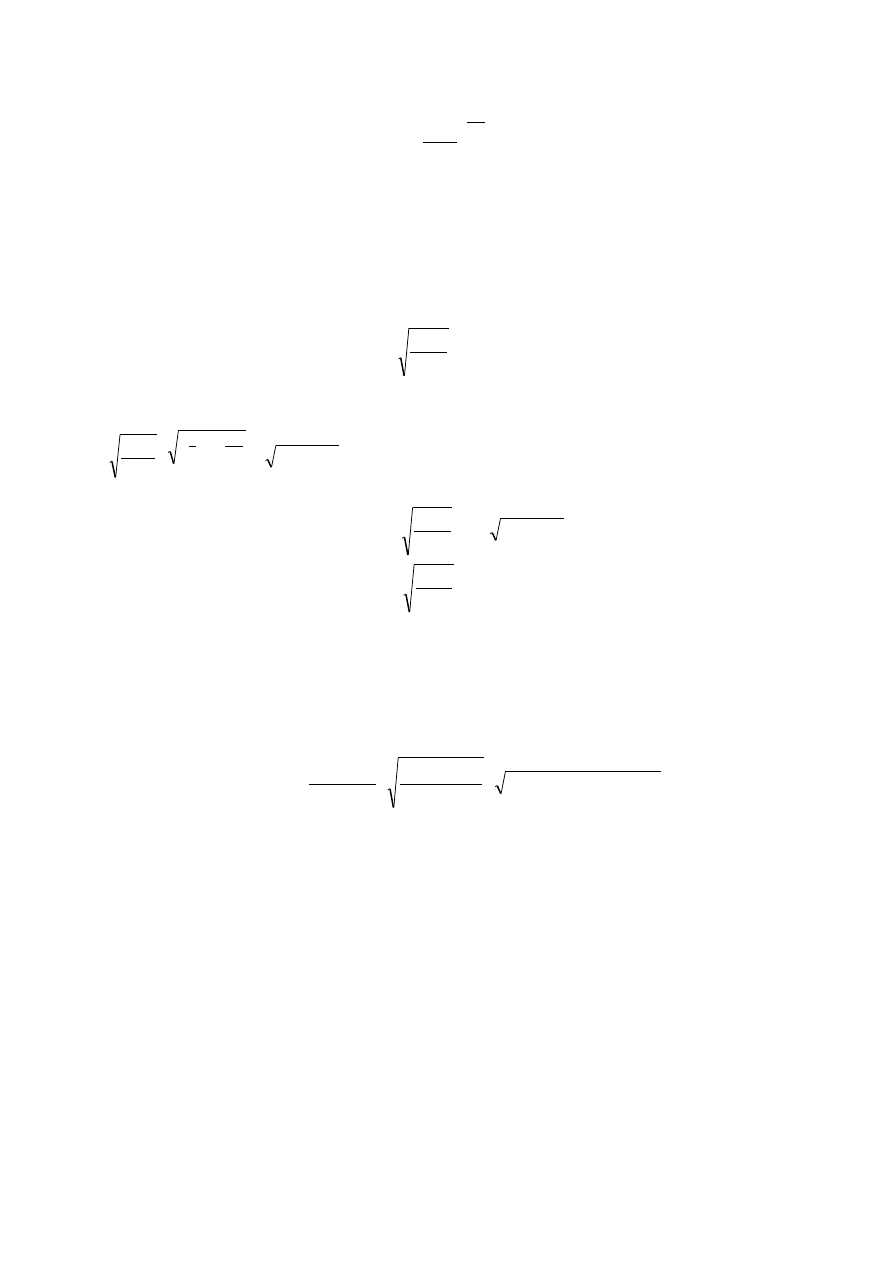
5

Funkcja

 





ma maksimum dla

1

1

2





















n

n

k

n





.

Dla:

-

4

,

1



n

528

,

0



k



 

484

,

0



k





-

3

,

1



n

546

,

0



k



 

472

,

0



k





-

2

,

1



n

565

,

0



k



 

459

,

0



k





-

1

,

1



n

585

,

0



k



 

444

,

0



k





Dla

1









k

(przepływ dokrytyczny) wykorzystuje się model (5), a dla

k









0

(przepływ krytyczny) model

 

k

p

T

R

f

G



















1

1

2

(5’)

Ze względu na złożoną postać funkcji

 





, dla

4

,

1



n

(przemiana adiabatyczna)

wykorzystuje

się

też

jej

aproksymację

zaproponowaną

przez

Prandtla



























1

1

1

2

n

n

n

n

n

, łącznie z założeniem, że

5

,

0



k



.

Założenia te prowadzą do tzw. uproszczonego wzoru de Saint-Venanta-Wentzela:

- dla

1









k



























1

2

1

1

p

T

R

f

G

(6)

- dla

k









0

5

,

0

2

1

1













p

T

R

f

G



(6’)

W modelach przepływów (2)



(6) jedynym parametrem charakteryzującym zdolności

przepływowe oporu jest jego efektywna powierzchnia przepływowa

f





.

Wykorzystując wzór Bernoulliego (2) wprowadzono inny parametr charakteryzujący
zdolności przepływowe oporu – tzw. współczynnik przepływu

]

/

[

3

h

m

k



[3,7]. Wartość

strumienia masy określa się ze wzoru





]

[

]

[

]

[

]

/

[

7

,

184

]

/

[

]

/

[

2

1

2

1

3

3

Pa

p

p

Pa

p

K

T

m

kg

h

m

k

h

kg

G

N















(7)

gdzie:

N



- gęstość gazu w warunkach znormalizowanej atmosfery odniesienia

(

K

T

N

15

,

293



,

kPa

p

N

100



) .

Współczynnik



k jest to wyrażona w m

3

/h wartość strumienia objętości wody o temperaturze

od 5

0

C do 30

0

C, która przepływa przez dany opór (zawór) pod wpływem różnicy ciśnień

100000 Pa. Należy zwrócić uwagę, że wzór (7) jest wzorem liczbowym, tzn. że wartość
współczynnika liczbowego jest dostosowana do jednostek występujących we wzorze wielkości.
Współczynnik



k może być podawany w innych jednostkach strumienia objętości, np. w

dm

3

/min; wymaga to zmiany wartości współczynnika we wzorze (7).

Nie wnikając w interpretację fizyczną współczynnika



k

, na podstawie porównania wzorów

(7) i (2) można stwierdzić że wartość



k jest proporcjonalna do

f





, a modele (7) i (2) są

równoważne. Mając na uwadze wystąpienie w odniesieniu do wzoru (2) krytycznego

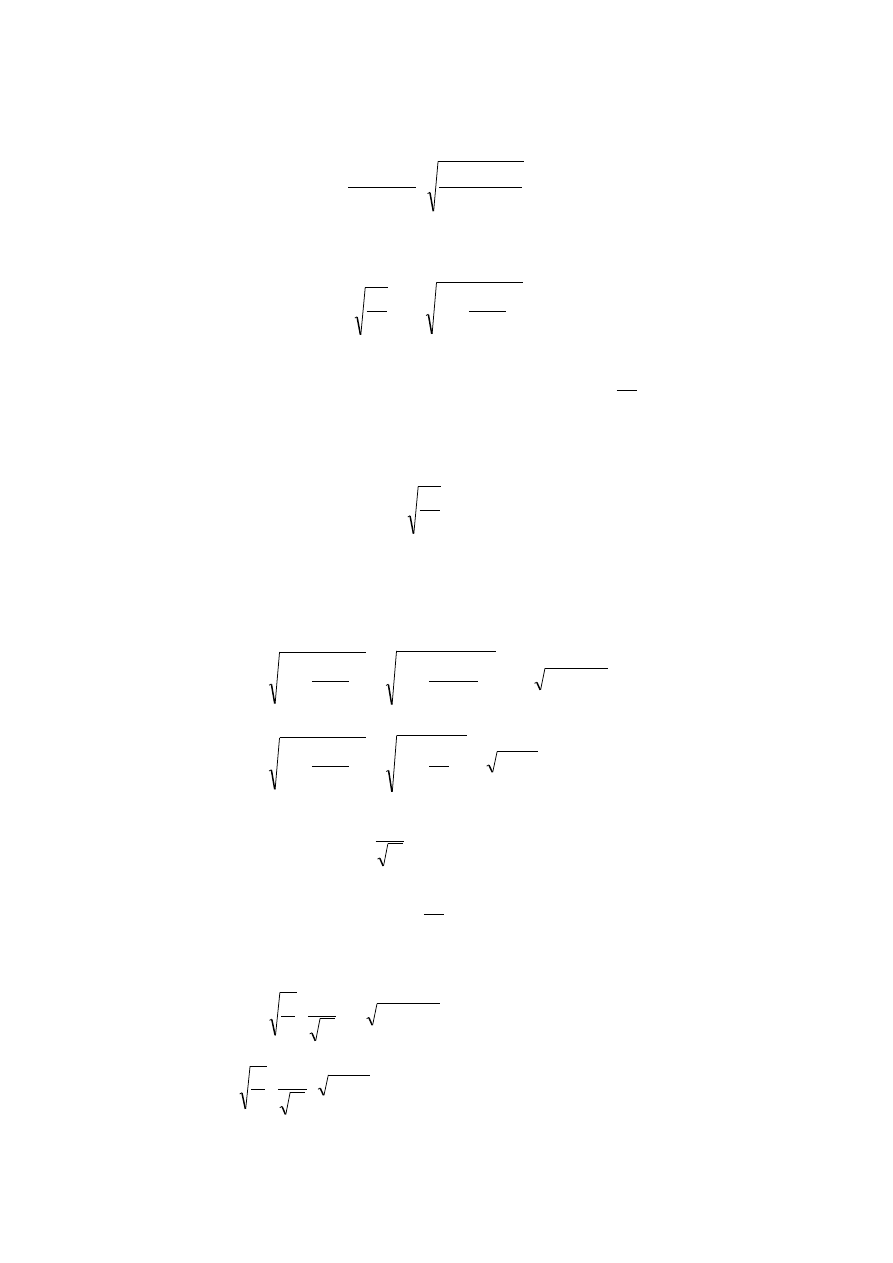
6

stosunku ciśnień

5

,

0



k



, model (7) wykorzystuje się tylko dla

1

5

,

0







, natomiast dla

5

,

0

0







obowiązuje zależność

]

[

]

[

]

/

[

4

,

369

]

/

[

]

/

[

1

1

3

3

Pa

p

K

T

m

kg

h

m

k

h

kg

G

N











(7’)

Inny model przepływu proponuje norma PN-92/M-73763 [5] (odpowiednik normy ISO 6358).
Wg PN-92/M-73763 strumień masy dla przepływów dokrytycznych oblicza się ze wzoru

2

1

1

1

1





























b

b

p

T

T

C

G

N

N





(8)

gdzie:

T

N

- temperatura znormalizowanej atmosfery odniesienia (

K

T

N

15

,

293



),

N



- gęstość

gazu w warunkach znormalizowanej atmosfery odniesienia,

1

2

p

p





,

b

- rzeczywisty

krytyczny stosunek ciśnień (największa wartość stosunku



, przy której w danym oporze

występuje jeszcze przepływ krytyczny). Wzór (8) należy stosować dla

1







b

.

Dla

b







0

(przepływ krytyczny) należy stosować wzór:

1

1

p

T

T

C

G

N

N











(8’)

Parametrami określającymi zdolności przepływowe oporu są w tym przypadku tzw.
przewodność dźwiękowa

C

oraz rzeczywisty krytyczny stosunek ciśnień

b

.

Łatwo zauważyć, że dla

5

,

0



b

model ten jest równoważny modelowi (6), ponieważ wtedy































 























1

2

5

,

0

5

,

0

1

1

1

2

2

b

b

Natomiast dla

0



b

model (8) jest równoważny modelowi (3), ponieważ wtedy

2

2

1

2

2

1

1

1

1











































p

p

b

b

.

Łatwo zauważyć, że wszystkie wymienione modele można sprowadzić do jednej struktury

 



B

T

p

A

G







1

1

gdzie współczynnik A reprezentuje parametr oporu wyrażający jego właściwości przepły-

wowe,

 



B

- funkcja stosunku ciśnień

1

2

p

p





.

Aby można było porównać właściwości przytoczonych modeli zapisano je w postaci, w której
maksymalna wartość funkcji

 

1





B

.

(2)

















 



 



2

2

1

2

2

5

,

0

1

1

B

A

T

p

R

f

G

























(3)













3

3

2

1

1

1

2

B

A

T

p

R

f

G

















0



k



7

(4)





























4

4

1

2

1

2

1

1

1

2

ln

ln

ln

2

B

k

k

A

k

k

T

p

R

f

G







































60653

,

0



k



(5)

































5

5

1

2

1

2

1

1

1

2

1

2

B

n

n

k

n

k

n

n

n

A

n

n

k

n

k

T

p

n

n

R

f

G











































1

1

2



















n

n

k

n



(6)

















 



 



2

6

6

1

2

2

5

,

0

1

1

B

B

A

T

p

R

f

G



























5

,

0



k



(7)





































2

7

7

1

2

]

[

]

[

]

/

[

7

,

184

]

/

[

5

,

0

]

/

[

1

1

3

3

B

B

A

N

K

T

MPa

p

m

kg

h

m

k

h

kg

G

























5

,

0



k



(8)



 



 









8

8

2

1

1

1

1

B

A

N

N

b

b

T

p

T

C

G

































b

k





(8)

















2

8

8

1

1

1

B

B

A

N

N

T

p

T

C

G























dla

5

,

0



b

(8)













3

8

8

2

1

1

1

B

B

A

N

N

T

p

T

C

G



















dla

0



b

Stosunek ciśnień [p2/p1]

0

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

1

0

0.2

0.4

0.6

0.8

1

B

B

B

B dla n = 1,4

2

3

4

5

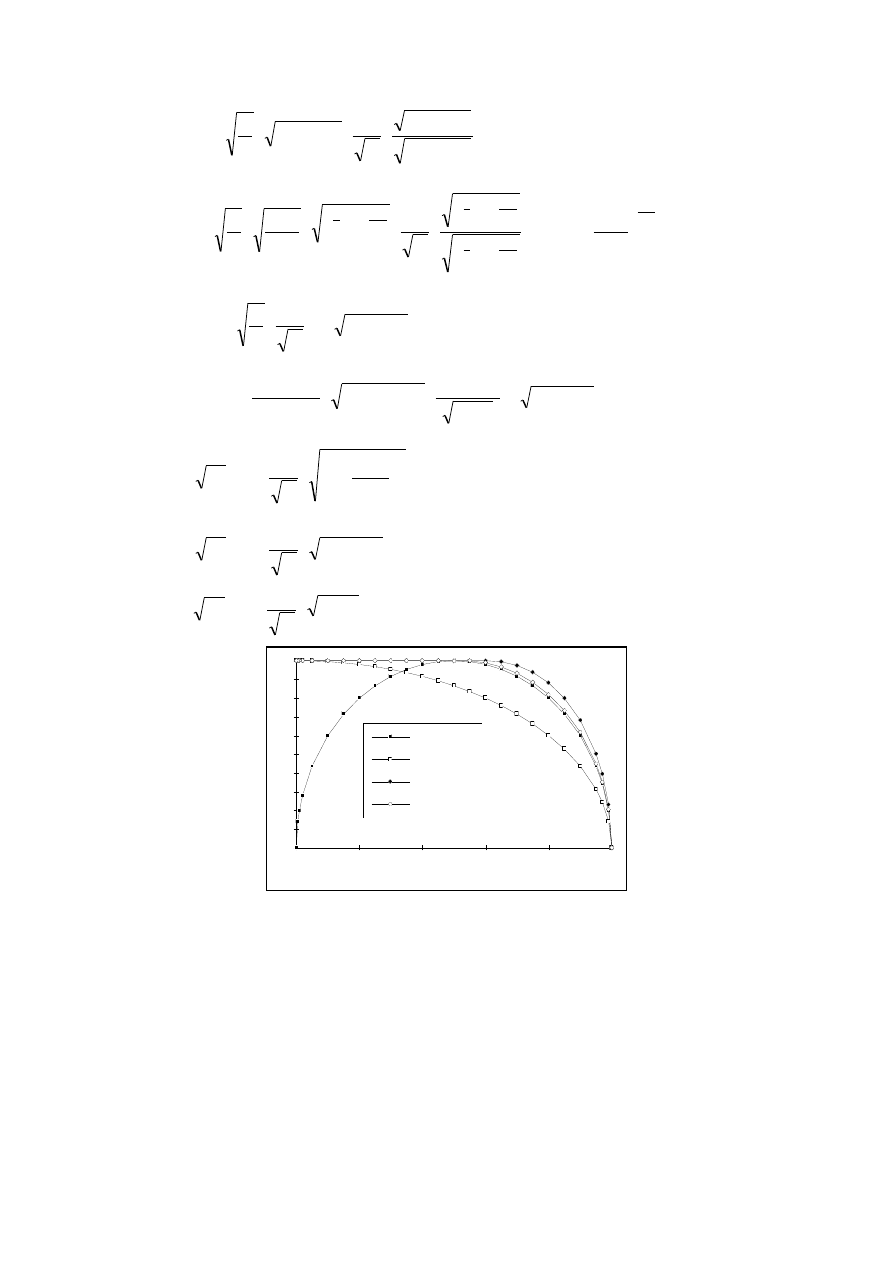
Rys.1. Porównanie różnych funkcji

 



B

8

Stosunek ciśnień [p2/p1]

0

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

1

0.5

0.6

0.7

0.8

0.9

1

n = 1,4

n = 1,3

n = 1,2

n = 1,1

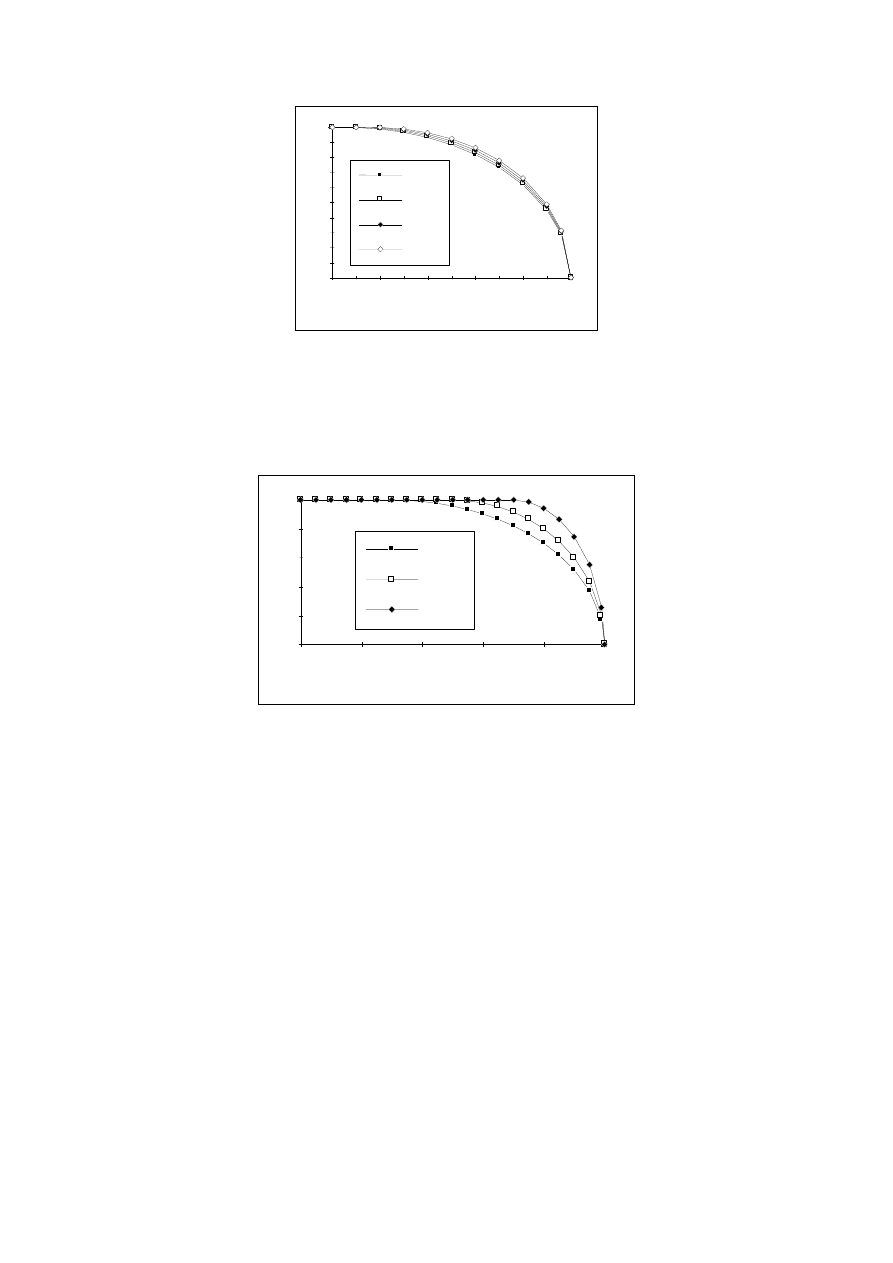
Rys.2. Porównanie przebiegów funkcji

 



5

B

dla różnych wartości wykładnika politropy

Porównanie różnych funkcji

 



B

pokazano na rys.1. Na rys. 2 pokazano przebiegi funkcji

 



5

B

dla różnych wartości wykładnika politropy, na rys. 3 - przebiegi funkcji

 



8

B

dla

różnych wartości współczynnika b .

Stosunek ciśnień [p2/p1]

0

0.2

0.4

0.6

0.8

1

0

0.2

0.4

0.6

0.8

1

b = 0,3

b = 0,5

b = 0,7

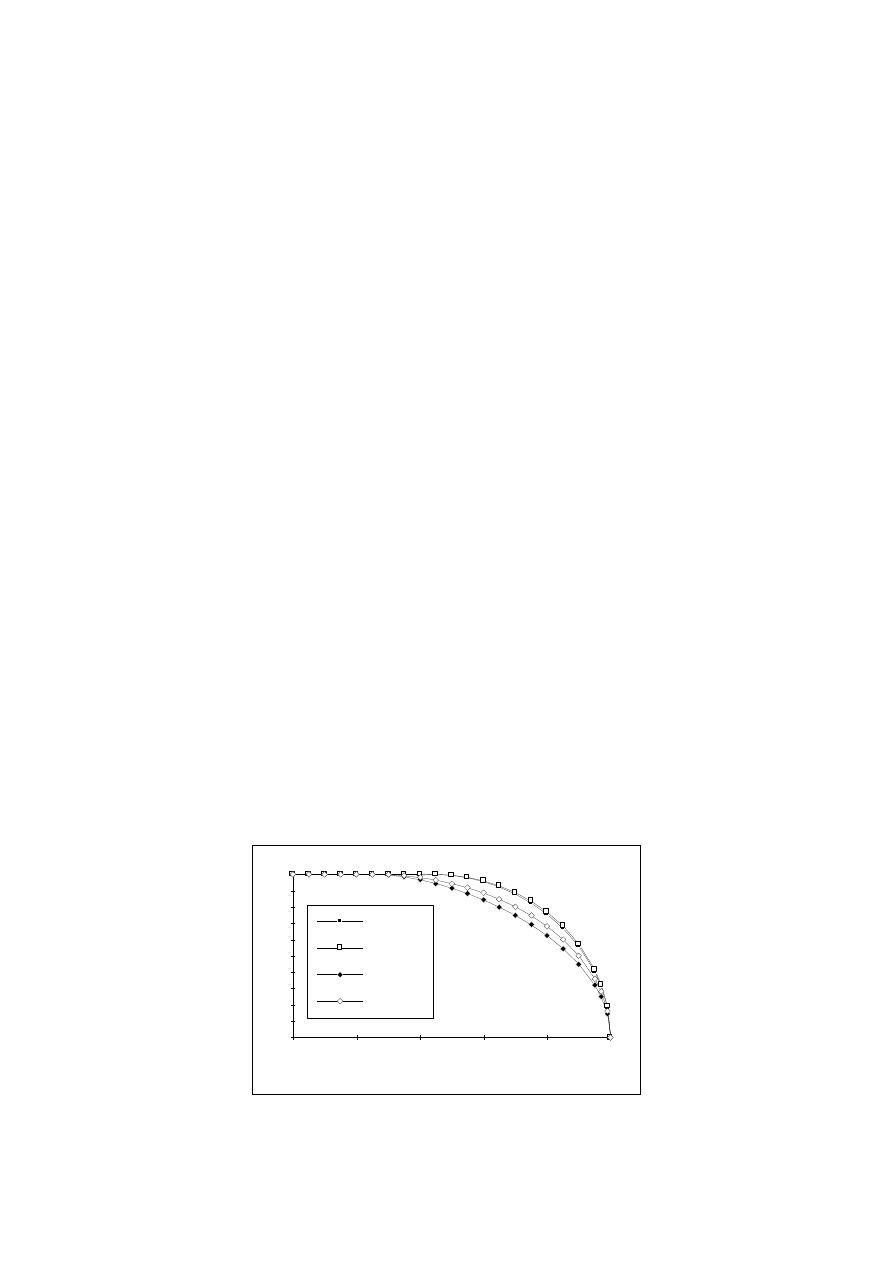
Rys.3. Porównanie przebiegów funkcji

 



8

B

dla różnych wartości współczynnika

b

Wartości współczynnika

A

dla wybranego modelu wyznacza się na podstawie zmierzonej

wartości strumienia masy

G

i warunków przepływu

1

p ,

1

T i



.

Porównując wzory o ujednoliconej strukturze można poczynić szereg spostrzeżeń.
1.

Modele (4)



(8) zakładają istnienie przepływów krytycznych - niezależnych od wartości

ciśnienia za oporem w określonych zakresach wartości stosunku ciśnień



.

Jeżeli współczynniki

A

tych modeli będą wyznaczone na podstawie pomiaru wartości

strumienia masy dla



, przy którym

1

8

7

6

5

4











B

B

B

B

B

, (przepływ krytyczny),

to wartości współczynników

4

A ,

5

A ,

6

A ,

7

A i

8

A będą jednakowe. Wtedy modele (4)



(8) w zakresie przepływów krytycznych będą identyczne (w tym zakresie wartości
stosunku



, w którym

1

8

7

6

5

4











B

B

B

B

B

).

Jeżeli natomiast strumień masy

G

zostanie zmierzony w warunkach przepływu dokry-

tycznego, to wyznaczone na tej podstawie wartości współczynników A będą różne,
zależne od rodzaju funkcji

)

(



B

występującej w danym modelu.

9

Zatem, aby współczynnik A charakteryzował opór niezależnie od przyjętego modelu
przepływu, należy go wyznaczać na podstawie wartości strumienia masy zmierzonej
w warunkach przepływu krytycznego (gdy

1

)

(





B

).

2.

Modele (6), (7) oraz model (8) dla

5

,

0



b

są identyczne, pomimo że właściwości

przepływowe oporu reprezentowane są przez różne parametry:

f





,



k ,

C

.

3.

Wartości efektywnej powierzchni przepływowej

f





wyznaczane na podstawie róż-

nych modeli są różne. Zatem współczynnik

f





nie jest współczynnikiem jedno-

znacznie charakteryzującym właściwości przepływowe oporu; należy go stosować tylko
dla modelu, na podstawie którego został wyznaczony.

4.

Wzór Bernoulliego - model (2) i uproszczony wzór de Saint-Venanta-Wentzela - model
(6) są modelami identycznymi.

5.

Model (3) i model (8) dla

0



b

są identyczne.

6.

W modelach (2), (3), (4), (6), (7) właściwości przepływowe oporu reprezentowane są
przez jeden tylko parametr:

f





albo



k ; w modelach (5) i (8) przez dwa parametry,

odpowiednio

f





i

n oraz

C

i

b

.

W przypadku modelu (5) zmiany parametru

n (od 1 do 1,4 - wykładnik politropy)

w niewielkim stopniu wpływają na wartości natężenia przepływu - w granicach 10 %
wartości tego natężenia (rys.2).
Większe zmiany parametru n nie mają fizycznego sensu, aczkolwiek rzeczywiste
zależności wartości przepływu od



często odpowiadają przebiegom funkcji

)

(

5



B

dla

wartości parametr n nie mających interpretacji fizycznej.
W przypadku modelu (8) funkcja

 



8

B

nie ma interpretacji fizycznej (tylko

geometryczną - ćwiartka elipsy), a parametr

b

oznacza doświadczalnie określoną

wartość

k



.

Można by, analogicznie jak w przypadku funkcji

 



8

B

, odstąpić od fizycznej interpre-

tacji funkcji

)

(

5



B

i wykorzystywać w szerszym niż dotychczas zakresie zmian

parametru

n , co umożliwiłoby lepsze dostosowanie modelu (5) do rzeczywistych

właściwości oporu. Przykładowo na rys. 4 pokazano przebiegi funkcji

)

(

5



B

dla

2



n

i

5



n

oraz odpowiadające im przebiegi funkcji

 



8

B

.

Stosunek ciśnień [p2/p1]

0

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

1

0

0.2

0.4

0.6

0.8

1

n = 2

b = 0,444

n = 5

b = 0,2533

Rys.4. Porównanie przebiegów funkcji

B

5

i odpowiadających im przebiegów funkcji

B

8

10

Powyższe wnioski sformułowano jedynie na podstawie matematycznej postaci poszcze-
gólnych modeli, bez oceny zgodności tych modeli z rzeczywistymi zależnościami przepływu
od warunków przepływu. Wykazanie wzajemnych relacji pomiędzy poszczególnymi
modelami pozwala na ocenę przydatności poszczególnych modeli i umożliwia racjonalny
wybór modelu najkorzystniej wyrażającego właściwości danego oporu rzeczywistego.

Literatura

1. Bukowski J., Kijkowski P.: Kurs mechaniki płynów. PWN, Warszawa 1980
2. Holejko D., Lammel L., Niewczas W., Żelazny M.: Pneumatyczne urządzenia automatyki.

Wydawnictwa Politechniki Warszawskiej, Warszawa 1986

3. Iwaszko J.: Funkcja przejścia pomiędzy parametrami C i b opisanymi w ISO 6358 a

współczynnikiem wymiarowym K

v

dla elementów pneumatycznych. Hydraulika i

Pneumatyka 4/1999

4. Kościelny W., Woźniak C.: Modele charakterystyk przepływowych oporów

pneumatycznych. IX Krajowa Konferencja PNEUMA’95. Mat. konf. str. 73 - 82

5. PN-92/M-73763 (ISO 6358-1989) Napędy i sterowania pneumatyczne. Elementy

pneumatyczne. Wyznaczanie parametrów przepływowych

6. PN-92/M-73703 (ISO 8778) Napędy i sterowania pneumatyczne. Znormalizowana

atmosfera odniesienia

7. Stelmach J.: Projektowanie przemysłowych układów automatyki. WNT, Warszawa 1980