
Egzamin dla Aktuariuszy z 14 maja 2007 r.
Matematyka Finansowa
Zadanie 1
?
)
(
40
)
(
42
2
1
,
0
1
=
−
=
−
d
N
e
d
N
P
C
δ
R
S
C
P
Xe
P
P
P
−
+
−
=
1
,
0
40
42
03
,
1
−
+
−
=
e
P
C
84
,
6
40
03
,
1
42
1
,
0
≈
−
+
=
−
e
P
C
Zadanie 2
ú
ú
ú
û
ù
ê
ê
ê
ë
é
+
+
+
=
+
+
+
=
∞
∞
∞
4
4
8
4
4
7
6
)
(
2
2
...
3
1
2
1
1
1
...
3
1
2
1
v
f
v
v
i
a
v
va
a
ODP
)
(
...
3
1
2
1
)
(
3
2
v
g
v
v
v
v
v
f
=
+
+
+
=
⋅
64
1
1
ln
1
1
)
1
1
1
ln(
)
1
ln(
)
(
)
1
ln(
)
(
)
(
1
1
...
1
)
(
2
≈
+
+
=
+
+
−
−
=
−
−
=
→
→
−
−
=
′
=
→
−
=
+
+
+
=
′
ò
i
i
i
i
i
i
v
v
v
f
v
v
g
v
g
v
v
v
v
g
Zadanie 3
....
)
1
(
3
)
1
(
2
)
1
(
)
(
....
)
1
(
1
)
(
4
3
3
2
2
1
2
2
1
−
+
−
+
−
+
−
=
′
+
+
+
+
=
i
R
i
R
i
R
i
V
P
i
R
i
R
i
PV
i
i
i
PV
i
R
i
R
dur
i
PV
i
i
i
i
V
P
+
=
+
+
+
+
=
←
+
−
=
+
′
1
)
(
...
)
1
(
2
)
1
(
)
(
1
)
1
)(
(
2
2
1
Z tego wynika:
i
i
PV
i
V
P
i
i
PV
i
V
P
1
)
(
)
(
)
(
)
(
−
=
′
−
=
′
2
2
)
(
)
(
)
(
)
(
)
(
i
i
PV
i
i
V
P
i
i
PV
i
i
V
P
i
V
P
+
′
−
=
−
′
−
=
′′
200
1
,
0
2
2
1
)
(
)
(
2
2
2
=
=
=
+
′
−
=
i
i
i
i
PV
i
V
P
ODP

Zadanie 4
(i)
TAK:
∏
∏
=
=
−
+
+
+
+
+
+
=
+
+
=
+
+
=
n
i
n
i
n
i
i
n
n
n
X
X
X
s
X
X
n
a
X
X
n
a
1
2
1
1
1
)
1
(
...
)
1
(
)
1
(
)
1
)...(
1
(
1
)
(
)
1
)....(
1
(
)
(
&
&
(
)
[
]
[
]
n
n
n
i
n
i
i
i
s
i
X
E
X
E
n
a
2
2
2
2
2
)
1
(
)
2
1
(
)
1
(
1
)
(
var
+
−
+
+
+
=
+
−
+
=
(ii)
TAK:
( )
)
1
(
...
)
1
(
)
1
(
1
i
i
i
s
E
n
n
n
+
+
+
+
+
+
=
−
&
&
(iii)
NIE:
Zał,
ż
e
)
1
;
0
(
~
J
X
i
ò
=
+
=
+
=
÷÷
ø
ö
çç
è
æ
+
1
0
1
0
2
ln
)
1
ln(
1
1
1
1
x
x
X
E
i
ale
n
n
−
+
≠
)
5
,
0
1
(
)
2
(ln
Zadanie 5
s
t
w
t
s
+
+
+
+
=
÷
ø
ö
ç
è
æ
+
+
ò
α
α
α
1
1
1
1
exp
ò
ò
>
+
+
+
+
+
+
+
+
+
+
+
=
′
+
+
+
+
+
+
+
+
+
=
t
t
t
t
t
t
x
t
ds
s
s
s
s
x
t
x
t
ds
s
t
s
s
s
x
t
x
0
0
0
1
1
1
1
1
)
(
)
1
(
1
1
1
)
(
)
(
1
1
1
1
1
)
(
)
(
α
α
α
α
α
α
α
α
0
)
1
(
1
)
(
1
)
(
1
1
1
)
(
)
(
2
>
+
+
+
′
+
+
+
+
=
′′
t
t
x
t
t
t
x
t
t
t
t
x
t
x
α
α
+
=
′
=
=
1
1
)
0
(
2
)
1
(
1
)
0
(
x
e
x
x
1
)
1
(
bo
1
1
2
1
1
2
2
)
1
(
1
1
1
)
1
(
2
<
ï
ï
î
ïï
í
ì
+
>
+
+
<
→
+
+
+
=
=
o
e
e
o
x
e
α
α
α
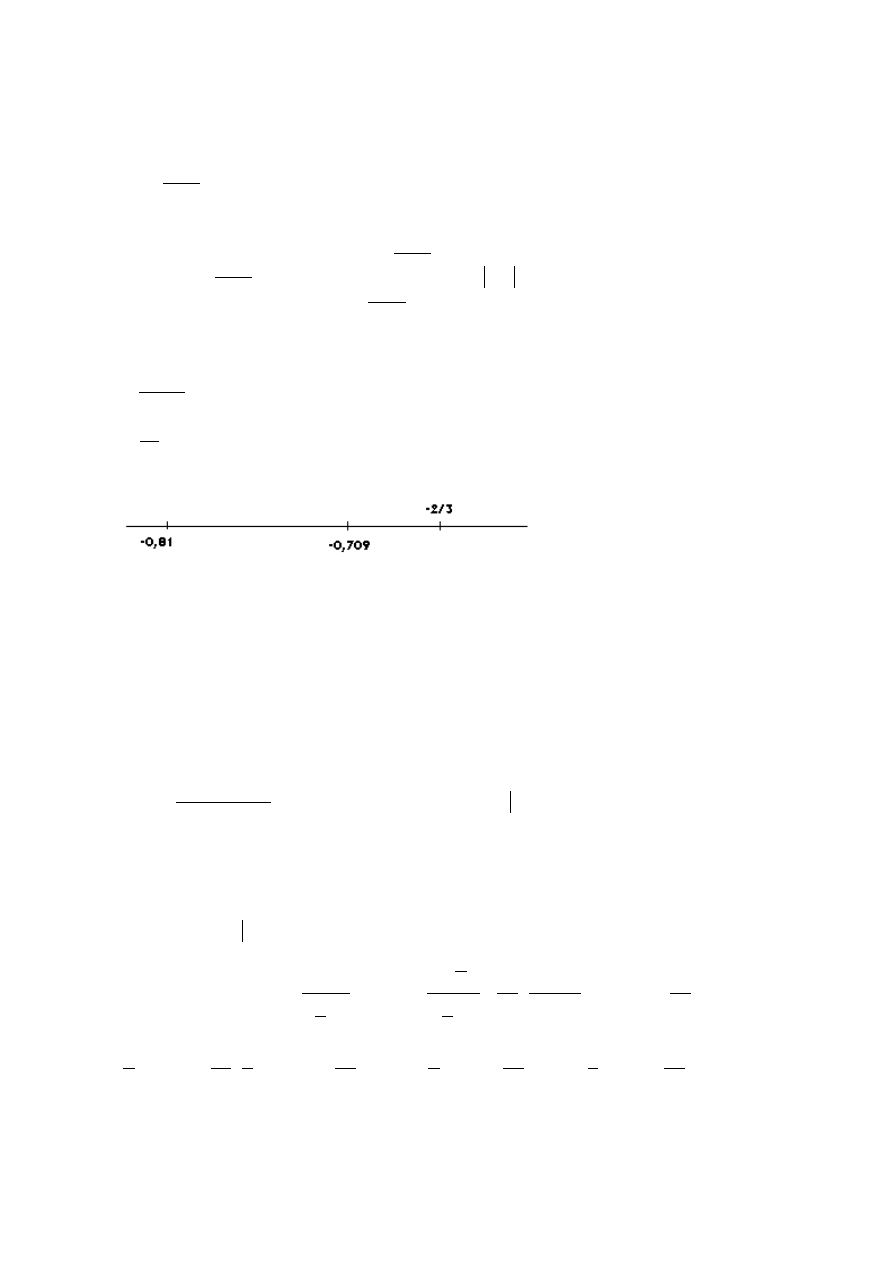
Z tego wynika:
81
,
0
1
2
1
709
,
0
1
2
2
1
−
≈
−
>
−
≈
−
−
<
e
e
α
α
Z tego wynika około -2/3
Zadanie 6
)
0
;
50
max(
)
0
;
50
max(
−
=
−
=
Y
B
X
A
)
5
,
1
;
3
/
2
(
~
X
X
J
Y
15
,
1
)
;
max(
B
A
E
CENA
=
ò
=
)
(
)
;
max(
)
;
max(
X
f
X
B
A
E
B
A
E
I.
X>50
{
}
[
]
50
20
23
60
5
3
90
20
27
20
5
2
50
2
75
8
9
5
6
)
50
(
5
2
50
2
5
,
1
50
2
)
5
,
1
(
5
6
6
5
3
2
)
50
(
6
5
50
)
(
)
50
(
)
50
(max
50
max
)
0
;
50
max(
))
0
;
50
max(
50
(
)
50
(
))
0
;
50
max(
;
50
max(
2
2
5
,
1
2
2
−
=
+
−
−
+
−
=
÷÷
ø
ö
çç
è
æ
+
−
−
+
−
=
=
÷÷
ø
ö
çç
è
æ
+
−
⋅
−
+
−
−
=
−
+
<
−
=
=
−
>
−
>
−
+
+
−
>
−
−
=
−
−
ò
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
y
X
Y
P
X
X
P
X
Y
E
Y
X
P
X
Y
X
E
x
x
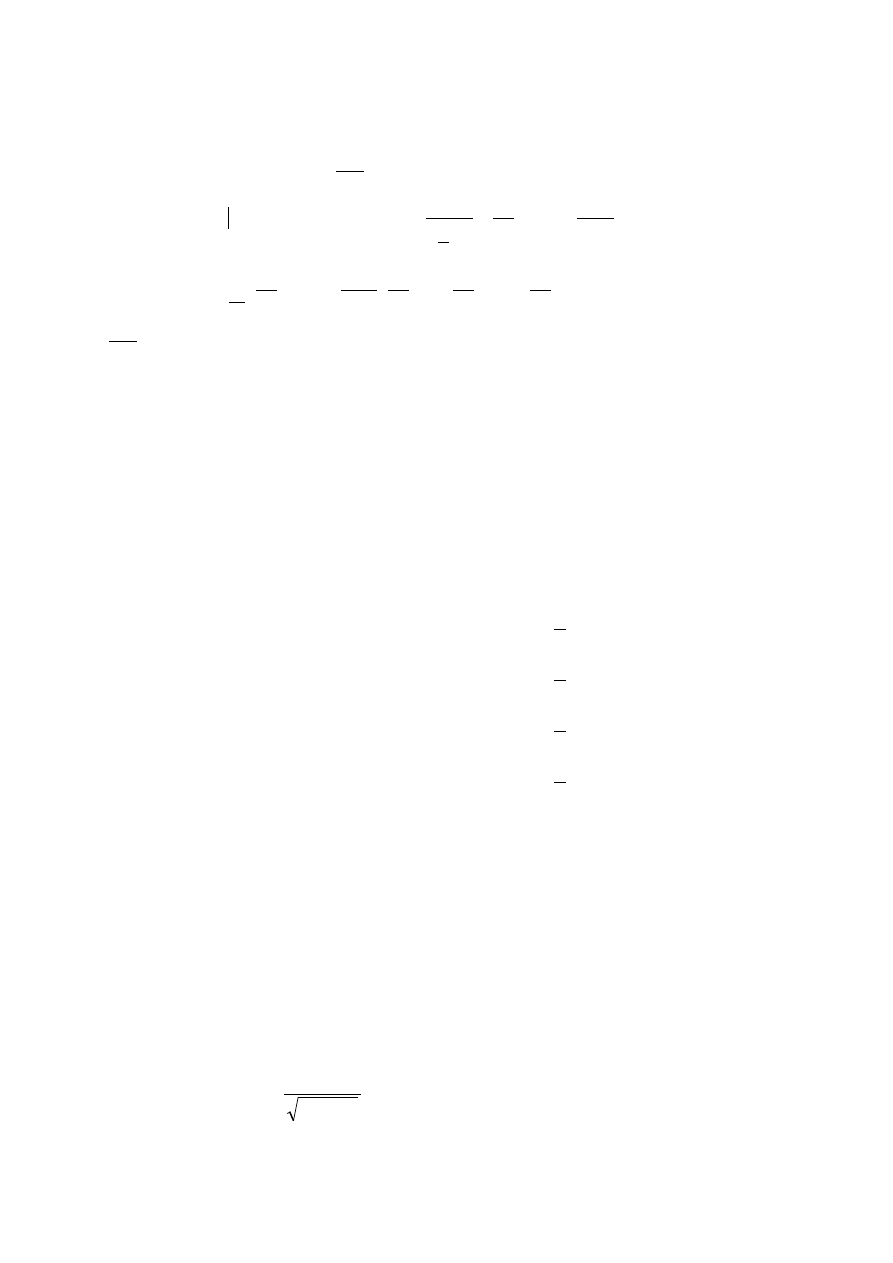
II.
x<50
[
]
[ ]
)
0
(
50
b
a;
~
Y
inaczej
3
100
))
0
;
50
max(
;
0
max(
=
<
>
−
b
x
Y
E
[
]
ò
+
−
=
−
=
>
>
−
x
x
x
x
y
P
Y
E
5
,
1
50
1500
90
20
27
6
5
50
)
0
(max
0
max
)
0
;
50
max(
[
]
ò
ò
≈
÷
ø
ö
ç
è
æ
−
+
÷
ø
ö
ç
è
æ
+
−
=
50
3
100
70
50
40
1
50
20
23
40
1
1500
90
20
27
)
;
max(
C
x
x
x
B
A
E
25
,
9
15
,
1
≈
C
Zadanie 7
1
:
10
6
=
a- podwojenie
b- tak samo
c- bankructwo
kwota
prawdopod
kwota na koniec
aaa
8
3
4
,
0
P(0)=0,488
aab
4
3
4
,
0
064
,
0
1
=
÷
ø
ö
ç
è
æ
n
P
aac
0
2
,
0
4
,
0
2
⋅
192
,
0
2
=
÷
ø
ö
ç
è
æ
n
P
aba
4
3
4
,
0
192
,
0
4
=
÷
ø
ö
ç
è
æ
n
P
i
X
~
abb
2
3
4
,
0
064
,
0
8
=
÷
ø
ö
ç
è
æ
n
P
abc
0
...
ac
0
...
baa
4
...
bab
2
...
bac
0
...
bba
2
...
bbb
1
...
bbc
0
...
bc
0
...
c
0
...
(
)
÷
÷
ø
ö
ç
ç
è
æ
−
>
=
>
≥
>
−
+
+
å
i
i
i
n
X
n
nEX
N
P
X
P
X
X
P
var
5
,
1
5
,
1
99
,
0
)
5
,
0
1
....
(
1
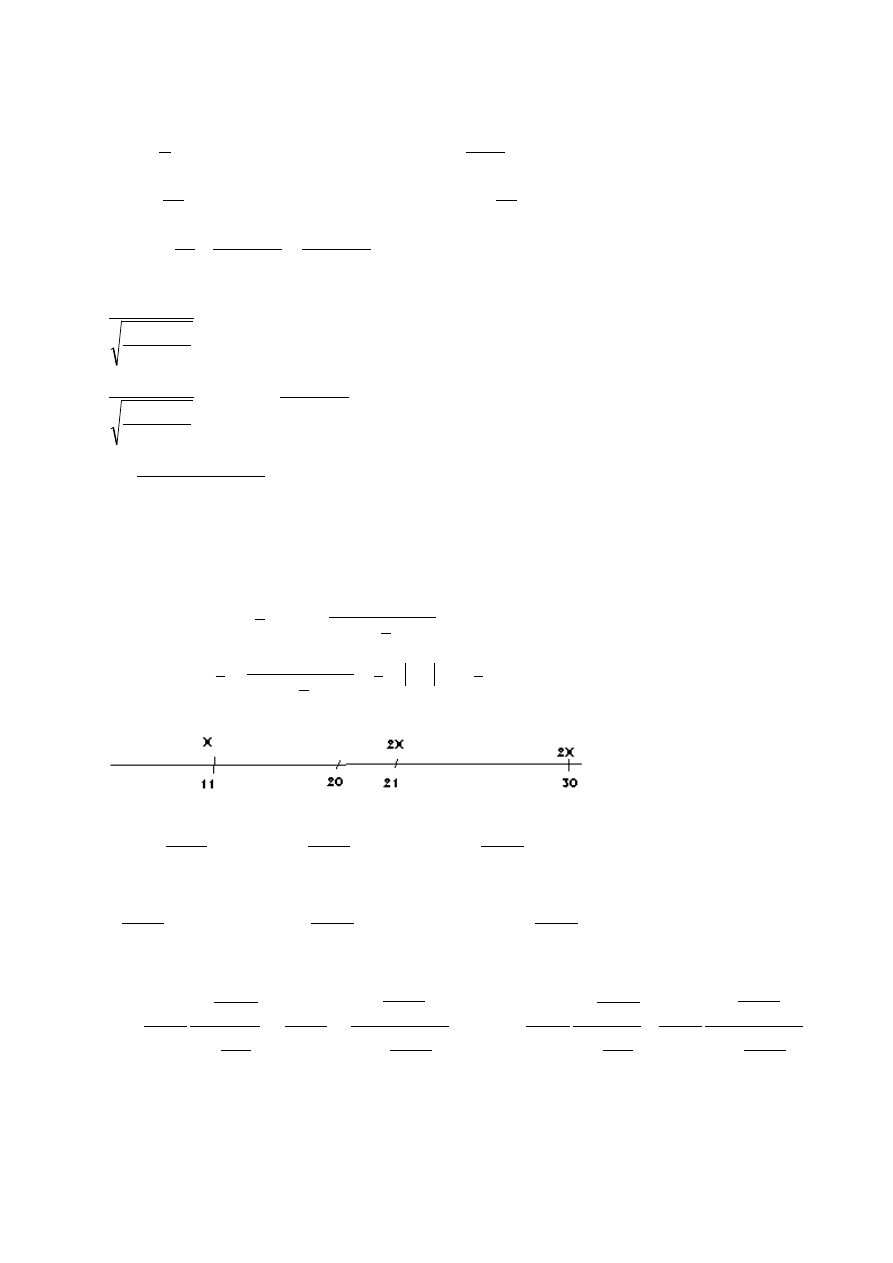
(
)
(
)
2
2
2
2
2
2
014016
,
5
985984
,
2
8
var
8
064
,
0
064
,
0
64
192
,
0
16
192
,
0
4
1
728
,
1
064
,
0
064
,
0
8
192
,
0
4
192
,
0
2
1
n
n
n
X
n
n
EX
n
n
EX
i
i
i
=
−
=
=
+
⋅
+
⋅
+
⋅
=
=
+
⋅
+
⋅
+
⋅
=
2
2
326
,
2
014016
,
5
228
,
0
326
,
2
014016
,
5
228
,
0
326
,
2
014016
,
5
728
,
1
5
,
1
>
→
>
−
≤
−
n
n
n
522
83
,
521
228
,
0
014016
,
5
326
,
2
2
2
=
→
≈
⋅
≥
n
n
Zadanie 8
K
=
⋅
10
08
,
1
400000
- kredyt po 10 latach
20
10
20
10
08
,
1
400000
08
,
1
400000
a
X
Xa
⋅
=
→
=
⋅
rata
X
Y
Ya
def
a
a
Xa
ZAD
=
→
=
=
⋅
⋅
=
=
10
10
20
10
10
08
,
1
400000
)
20
(
dodatkowa rata
(
)
(
)
(
)
+
−
+
+
−
+
−
=
30
30
12
12
11
11
996
,
0
1
05
,
1
...
996
,
0
1
05
,
1
996
,
0
1
05
,
1
X
X
X
ODP
)
996
,
0
1
(
996
,
0
05
,
1
...
)
996
,
0
1
(
996
,
0
05
,
1
)
996
,
0
1
(
996
,
0
05
,
1
10
20
30
2
20
22
20
21
−
+
+
−
+
−
+
X
X
X
]]
05
,
1
996
,
0
1
05
,
1
996
,
0
1
05
,
1
996
,
0
05
,
1
1
1
05
,
1
1
1
05
,
1
1
[
996
,
0
05
,
1
996
,
0
1
05
,
1
996
,
0
1
05
,
1
996
,
0
05
,
1
1
1
05
,
1
1
1
05
,
1
1
[
10
21
10
21
20
20
11
20
11
−
÷
ø
ö
ç
è
æ
−
−
−
−
+
−
÷
ø
ö
ç
è
æ
−
÷
ø
ö
ç
è
æ
−
−
−
=
X
Z tego wychodzi około 53706

Zadanie 9
7
7
15
7
15
7
)
1
(
05
,
1
06
,
1
)
1
(
06
,
1
1000
05
,
1
1000
x
x
+
=
+
⋅
ú
ú
ú
ú
û
ù
ê
ê
ê
ê
ë
é
−
+
=
4
4
3
4
4
2
1
A
x
E
ODP
1
05
,
1
)
1
(
06
,
1
;
06
,
0
min
15
7
7
bo korzy
ść
emitenta ma by
ć
05
,
0
06
,
0
<
⇔
<
x
A
[
]
ò
ò
≈
⋅
+
⋅
−
ú
û
ù
ê
ë
é
−
⋅
=
+
−
=
05
,
0
04
,
0
08
,
0
05
,
0
15
22
15
22
15
7
%
94
,
5
03
,
0
5
,
1
01
,
0
25
04
,
1
05
,
1
22
15
05
,
1
06
,
1
25
04
,
0
06
,
0
1
...
06
,
1
04
,
0
1
ODP
Zadanie 10
0385
,
0
1
12
,
1
35
,
0
78
,
0
4
,
0
03
,
1
25
,
0
082
,
0
1
02
,
1
35
,
0
2
,
1
4
,
0
98
,
0
25
,
0
1065
,
0
1
84
,
0
35
,
0
3
,
1
4
,
0
17
,
1
25
,
0
0675
,
0
1
13
,
1
35
,
0
03
,
1
4
,
0
04
,
1
25
,
0
4
3
2
1
−
=
−
⋅
+
⋅
+
⋅
=
=
−
⋅
+
⋅
+
⋅
=
=
−
⋅
+
⋅
+
⋅
=
=
−
⋅
+
⋅
+
⋅
=
r
r
r
r
0
0
850
4
94
,
0
052
,
0
850
3
95
,
0
0765
,
0
850
2
96
,
0
0375
,
0
850
1
=
⋅
=
⋅
⋅
=
⋅
⋅
=
⋅
⋅
=
A
A
A
A
48
,
33
4
4
3
2
1
≈
+
+
+
=
A
A
A
A
ODP
Wyszukiwarka
Podobne podstrony:
2007 05 14 praid 25651 Nieznany
2007 01 08 matematyka finansowaid 25640
2007 05 14 prawdopodobie stwo i statystykaid 25652
2003 05 17 matematyka finansowaid 21697
2010.05.31 matematyka finansowa
2007.01.08 matematyka finansowa
2007.10.08 matematyka finansowa
2007.05.14 prawdopodobie stwo i statystyka
2005 05 16 matematyka finansowaid 25340
mat fiz 2007 05 14
1 2010 05 31 matematyka finansowaid 8925
2005.05.16 matematyka finansowa
2007 12 03 matematyka finansowaid 25661
2007 10 08 matematyka finansowaid 25658
2007 05 14 Uzasadnienie TK do Ustawy lustracyjnej
więcej podobnych podstron