
Egzamin dla Aktuariuszy z 8 października 2007 r.
Matematyka Finansowa
Zadanie 1
i
MARGINES
DOPŁATA
PRZYCHÓD
DYSKONTO
0
180
180
DOPŁATA(i)
i
1
,
1
/
1
18
,
0
1050
⋅
MAR(i)-PRZ(i)
04
,
1
180
⋅
.....
2
18
,
0
05
,
1
1050
1
−
⋅
i
.....
M(i-1)1,04
.....
3
....
......
.....
.....
....
.....
......
......
......
6
0
.......
M(5)1,04
6
1
,
1
/
)
(i
DOP
SUMA
≈
53
Zadanie 2
( )
[
]
( )
( )
( )
n
n
k
k
n
n
n
n
n
k
k
n
n
n
Ia
v
k
Ia
v
n
v
v
v
Da
v
k
k
n
Da
nv
v
n
v
n
nv
å
å
=
=
=
+
+
+
+
=
−
−
=
+
+
−
+
−
+
=
1
2
2
3
2
2
2
1
3
2
...
3
2
)
1
(
...
3
)
2
(
2
)
1
(
β
α
( )
( )
i
a
n
Da
i
nv
a
Ia
n
n
n
n
n
−
=
−
=
&
&
( ) ( )
TAK
(ii)
OCZYWISTE
)
1
(
→
+
=
+
n
n
n
a
n
Ia
Da
( )
( )
[
]
[
]
( )
å
å
å
å
=
=
+
=
+
=
+
=
=
+
−
+
=
−
−
+
=
+
n
k
n
k
k
n
k
k
k
n
n
n
n
Ia
n
kv
n
v
k
nk
v
k
k
nk
k
v
k
k
n
k
Ia
Da
1
1
2
2
2
)
1
(
)
1
(
)
(
)
(
)
1
(
.
1
β
α
( )
( )
( )
( )
( ) ( )
wagi
inne
bo
NIE
)
(
)
1
(
)
(
i
Ia
Da
Ia
Da
a
n
Ia
Da
a
dur
n
n
n
n
n
n
n
n
n
n
n
n
→
+
+
=
+
+
=
β
α
β
α
Z 1 wynika:
( ) ( )
[
]
( )
n
n
n
n
n
n
a
n
Ia
n
Ia
Da
)
1
(
1
+
=
+
−
+
=
α
β
( )
TAK
iii
n
n
n
n
a
Ia
n
n
n
n
n
n
n
)
(
1
)
1
(
1
1
1
→
−
+
+
+
=
−
+
+
+
=
β
α
α
α
β
[
]
( )
( )
( )
å
=
+
+
−
−
−
−
=
−
−
=
n
k
n
n
n
n
n
k
n
Ia
v
v
n
a
Ia
Ia
n
v
k
k
n
LICZNIK
1
1
2
1
2
)
)
1
(
(
)
(
α

no
ś
o
ś
niesko
ń
ies
do
mianownik
a
0
do
licznik
bo
0
1
lim
lim
2
1
2
1
2
=
+
−
=
−
+
+
n
n
n
n
v
ni
i
v
n
i
a
n
v
n
( )
( )
( )
( )
( )
0
1
)
1
(
lim
1
1
lim
lim
0
1
1
1
lim
lim
1
1
1
1
1
1
lim
1
1
1
lim
lim
=
+
−
−
=
−
−
−
=
=
−
−
−
−
−
=
−
=
−
−
−
−
−
=
−
−
ú
û
ù
ê
ë
é
−
−
−
=
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
v
ni
i
v
i
v
n
v
Da
a
i
v
n
nv
v
v
Da
Ia
v
in
v
nv
v
v
i
v
n
nv
v
v
n
Da
n
Ia
St
ą
d wynika,
ż
e:
r
v
n
1
1
1
1
lim
+
=
−
=
α
Zadanie 3
Zakładamy,
ż
e S to suma płatno
ś
ci, z tego:
2
...
2
2
2
2
2
1
0
=
→
=
+
+
+
b
v
v
b
v
b
b
0
0
0
1
=
=
b
b
Z tego wynika,
ż
e S=2
Zadanie 4
( )
43
42
1
A
k
k
N
N
k
k
N
N
v
k
N
v
Nv
i
k
N
i
N
å
å
=
−
−
=
+
−
−
−
+
−
=
+
−
+
+
−
10
2
1
1
10
2
1
1
)
1
(
10
0
)
1
(
)
1
(
1
10
v
v
v
v
v
A
v
v
v
v
v
A
v
v
v
Av
v
v
v
A
−
−
−
−
=
−
+
+
+
=
−
+
+
+
=
+
+
+
=
1
9
)
1
(
1
9
...
)
1
(
9
...
2
9
...
2
11
2
9
2
11
10
3
2
11
4
3
10
3
2

0
9
9
10
20
10
)
1
(
9
)
1
(
)
2
1
(
10
1
9
)
1
(
1
10
11
10
10
1
1
1
10
9
1
2
1
11
2
9
2
1
1
=
+
−
−
+
−
+
−
=
=
−
−
−
+
+
−
−
=
÷÷
ø
ö
çç
è
æ
−
−
−
−
+
−
+
+
+
+
+
−
+
+
−
−
−
N
v
Nv
N
v
N
v
Nv
Nv
Nv
v
N
v
v
N
v
v
v
Nv
v
v
v
v
v
N
v
Nv
N
N
N
N
N
N
N
N
N
N
N
N
N
N
Nv
Nv
Nv
Nv
N
v
Nv
N
v
Nv
Nv
Nv
N
:
0
10
20
9
10
9
0
9
9
10
20
10
2
11
12
12
11
11
2
2
=
−
+
−
−
=
+
−
−
+
−
+
−
0
10
20
9
10
9
2
11
12
=
−
+
−
−
v
v
v
v
nie zale
ż
y od N , z tego wynika,
ż
e var=0
i sprawdzamy (B) i (E)
dla 30% wychodzi około -0,11
dla 45% wychodzi około - 0,55
Z tego wynika, ze (B) najbli
ż
ej
Zadanie 5
4
4
3
3
2
2
1
4
4
4
4
3
3
2
2
1
4
4
)
1
(
1
)
1
(
1
)
1
(
1
1
1
)
1
(
1
1
1000
)
1
(
1000
)
1
(
1000
)
1
(
1000
1
1000
)
1
(
1000
s
s
s
s
s
i
s
i
s
i
s
i
s
i
s
+
+
+
+
+
+
+
+
−
=
→
→
=
+
+
+
+
+
+
+
+
+
35
2
125
7
75
4
04
,
0
4
3
2
1
=
=
=
=
s
s
s
s
z tego wynika,
ż
e i około 5,7%
Zadanie 6
Wyliczenia pomocnicze:
1
2
)
1
(
2
2
−
=
−
−
n
n
n
...
95
,
0
3
95
,
0
2
95
,
0
95
,
0
3
2
2
2
1
2
+
+
+
=
⋅
=
å
∞
=
n
n
n
X
...
95
,
0
3
95
,
0
2
95
,
0
95
,
0
4
2
3
2
2
+
+
+
=
⋅
X
0,95
v
gdzie
2
...
95
,
0
95
,
0
2
...)
95
,
0
2
95
,
0
(
2
95
,
0
...
95
,
0
95
,
0
...)
95
,
0
3
95
,
0
2
(
2
95
,
0
...
95
,
0
)
1
3
2
(
95
,
0
)
1
2
2
(
95
,
0
...
95
,
0
)
2
3
(
95
,
0
)
1
2
(
95
,
0
05
,
0
2
2
3
2
3
2
3
2
3
2
2
2
2
2
=
−
=
=
−
−
⋅
−
+
⋅
+
+
=
−
−
−
+
⋅
+
⋅
+
=
=
+
−
⋅
+
−
⋅
+
=
+
−
+
−
+
=
⋅
∞
∞
a
Ia
X
v
v
a
v
v
Ia
−
=
−
=
∞
∞
1
)
1
(
2
14820
05
,
0
1
)
1
(
2
2
=
−
−
−
=
v
v
v
v
ODP
Zadanie 7
Zał: I(0)=1, L=1 KOSZT=K(1)-(1+r)
ï
ï
ï
ï
î
ïï
ï
ï
í
ì
=
=
=
⋅
=
⋅
=
⋅
=
=
⋅
=
=
=
=
=
0625
,
0
0,5
4096
,
0
8
,
0
25
,
0
5
,
0
4
6144
,
0
8
,
0
2
,
1
375
,
0
0,5
6
9216
,
0
8
,
0
2
,
1
25
,
0
0,5
4
3824
,
1
8
,
0
2
,
1
0625
,
0
0,5
0736
,
2
1,2
praw
...
4
4
4
3
4
2
2
4
3
4
4
cena
X
(
)
0625
,
0
25
,
0
375
,
0
216
,
1
25
,
0
3824
,
1
0625
,
0
0736
,
2
)
216
,
1
;
max(
+
+
⋅
+
⋅
+
⋅
=
X
E
KOSZT = Emax - 1,216
%
8
216
,
1
≈
=
KOSZT
ODP
Zadanie 8
0
)
1
(
10300
1
300
94
,
9717
04
,
1
05
,
1
10300
05
,
1
300
2
=
+
−
+
−
≈
⋅
+
=
r
r
C
C
%
5
,
4
04
,
1
0
20011
0
10300
300
1
0
10300
)
1
(
300
)
1
(
2
1
2
2
≈
→
≈
<
≈
∆
=
−
−
=
+
=
−
+
−
+
r
x
x
x
Cx
x
r
r
r
C
do oblicze
ń
bierzemy dokładne r
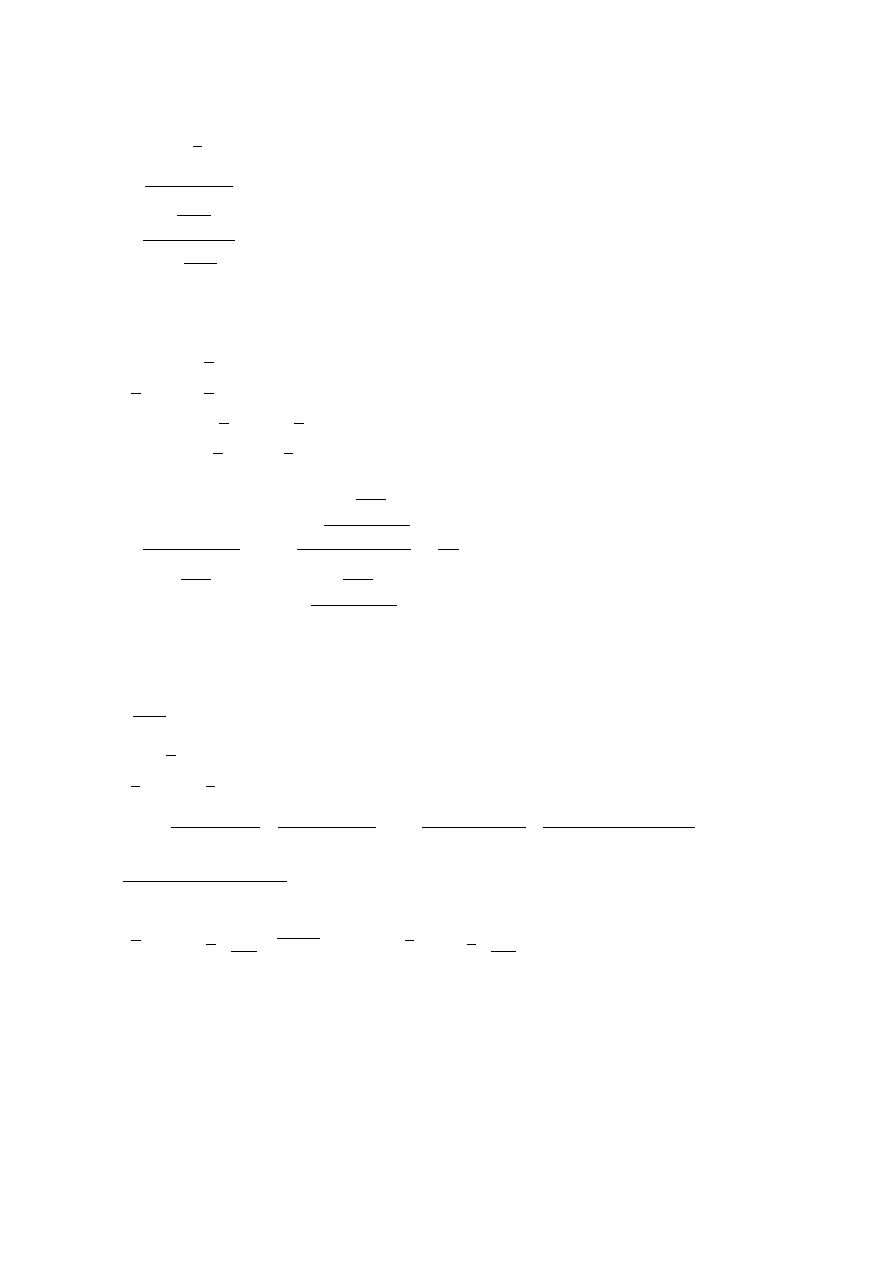
1284
1
1
1
1
1
1
10612
10612
312
04
,
1
300
10
10
≈
+
−
÷
ø
ö
ç
è
æ
+
−
=
=
=
⋅
r
r
X
a
X
&
&
Zadanie 9
04
,
0
;
20
05
,
0
;
32
05
,
0
;
40
500000
Ya
Xa
Xa
=
=
(
)
KAP
SKL
Xa
Xa
X
S
i
.
10
05
,
0
;
22
05
,
0
;
32
←
−
−
=
(
)
04
,
0
;
10
04
,
0
;
20
10
Ya
Ya
Y
S
r
−
−
=
%
140
04
,
0
04
,
1
1
1
05
,
0
05
,
1
1
1
05
,
1
1
1
05
,
0
500000
20
32
40
≈
→
÷
ø
ö
ç
è
æ
−
÷
ø
ö
ç
è
æ
−
⋅
=
÷
ø
ö
ç
è
æ
−
⋅
=
r
i
S
S
X
Y
X
Zadanie 10
B
A
Ba
Aa
Aa
X
v
v
i
=
→
=
=
−
=
06
,
0
;
15
06
,
0
;
15
06
,
0
;
30
1
30
15
15
16
15
30
30
2
2
04
,
1
)
995
,
0
1
(
995
,
0
...
04
,
1
)
995
,
0
1
(
995
,
0
04
,
1
)
995
,
0
1
(
...
04
,
1
)
995
,
0
1
(
04
,
1
)
995
,
0
1
(
18000
−
⋅
+
+
−
⋅
+
−
+
+
−
+
−
=
A
A
A
A
A
18000
995
,
0
04
,
1
1
04
,
1
995
,
0
;
15
04
,
0
;
15
15
15
04
,
1
995
,
0
;
30
04
,
0
;
30
=
ú
ú
û
ù
ê
ê
ë
é
−
+
−
=
=
v
v
a
a
A
Aa
Aa

198200
06
,
0
06
,
1
1
1
995
,
0
995
,
0
04
,
1
04
,
1
995
,
0
1
04
,
0
04
,
1
1
1
995
,
0
04
,
1
1
959
,
0
995
,
0
04
,
1
04
,
1
995
,
0
1
04
,
0
04
,
1
1
1
18000
30
1
15
15
15
15
30
30
≈
÷
ø
ö
ç
è
æ
−
=
→
→
ú
ú
ú
ú
ú
û
ù
ê
ê
ê
ê
ê
ë
é
÷
÷
÷
÷
÷
ø
ö
ç
ç
ç
ç
ç
è
æ
−
÷
ø
ö
ç
è
æ
−
−
÷
ø
ö
ç
è
æ
−
+
−
÷
ø
ö
ç
è
æ
−
−
÷
ø
ö
ç
è
æ
−
⋅
=
−
A
X
A
Wyszukiwarka
Podobne podstrony:
2007.10.08 matematyka finansowa
2007 01 08 matematyka finansowaid 25640
2007.01.08 matematyka finansowa
2004 10 11 matematyka finansowaid 25165
mat fiz 2007 10 08
1 2006 10 09 matematyka finansowaid 8919
1 2009 10 05 matematyka finansowaid 8924
2002 10 12 matematyka finansowaid 21647
2007.10.08 prawdopodobie stwo i statystyka
2008.10.06 matematyka finansowa
1 2009.10.05 matematyka finansowa
2004.10.11 matematyka finansowa
1 2006.10.09 matematyka finansowa
2010.10.04 matematyka finansowa
1 2000 04 08 matematyka finansowaid 8917
2003 10 11 matematyka finansowaid 21704
2007 05 14 matematyka finansowaid 25650
więcej podobnych podstron