Egzamin dla Aktuariuszy z 8 stycznia 2007 r.
Matematyka Finansowa
Zadanie 1
K
K = Ra
→ R =
240
a 240
1
2
12
3
24
ODP =
a∞ +
v a∞ +
v a∞ + .... =
a
a
a
240
240
240
a
æ
ö
∞
v
i
12
24
1
=
1 + 2 v + 3 v
+ ... =
≈ 86 9
,
çç 1
4
4
4
2
4
4
4
3 ÷
÷
a
è
I
ø 1− v 1
240
− v
1
(
12
− v )2
240
12
12
24
Iv
= v + 2 v + ...
1
1
12
12
24
I 1
( − v ) = 1 + v + v
+ ... =
→ I =
12
12
2
1 − v
1
( − v )
Zadanie 2
ODP P max
pK
1
( − p) K
K 1
( + i) =
max( X − 70 0
; ) +
max 7
( 0 − X 0
; )
3
12
p
1
( − p)
i =
max( X − 70 0
; ) +
max 7
( 0 − X 0
; ) −1
3
12
1 é 7 æ
0 1 − p
ö
9 æ
0
p
öù
Ei =
ê ç
ò
(70 − x) − ÷
1 +
ç ( x 70) 1
30
ò
−
− ÷ú
60 ë è 12
ø
70 è 3
øû
é
2
2
70
90
ù
1
1
p
p
2
æ −
ö
æ
ö
Ei =
ê ç
ò
(70 − x) − ÷
1
+ ç ( x 70) 1
30
ò
−
− ÷ ú
60 êë è 12
ø
70 è 3
ø úû
Z tego wynika:
Ei=0
Var(i)=..=
Parabola znaleźć współ. przy 2
p i p
= − b
ODP
− min
2 a
i wychodzi 33%
Zadanie 3
æ 1
1
ö
2
1
3
1 2
1
N ç
v +
v +
v + ...÷ > v +
v + v 3 + ...
è1⋅ 2
2 ⋅ 3
3 ⋅ 4
ø
2
3
1
4
4
4
2
4
4
4
3
X
æ 1 1 ö
ù
N êç − ÷ v + ç − ÷ 2
v + .. ú
. > X
ëè1 2 ø
è 2 3ø
û
é
1 2
1 3
1
1 2
ù
N v +
v + v + ... − v − v − ... > ê
ú X
ë
2
3
2
3
û
é
æ X
öù
X
N ê X − ç
− ÷
1 ú > X → N > ë
è v
øû
æ
X ö
ç1−
÷
è
9 ø
1
−
1
X = f i
( ) = 1
( + i) +
1
( + i)−2 + ...
2
−2
−3
2
v 2
3
1
1
1
f ′ i
( ) = − 1
( + i)
− 1
( + i)
− ... = − v − v − ... = −
= −
=
−
1 − v
1
( + i i
)
i + 1
i
i
f ( i) = ò
1 +
f ′( i) = ln
→ f ( i ) obliczamy i = 1
b
o v = 9
,
0
i
9
ODP : N > ,
3 0
9 c
zyli c
onajmniej 4
Zadanie 4
X ~ J (40 7
; 0)
Y ~ J ( X /
5
,
1
;
2
X )
E[max(max( X − 50 0
; ); max( Y − 50 0
; ))] = .. g
. dzi
e Z = max(max( X − 50 0
; ); MAX ( y − 50 0
; ))
Szukamy: E( E( Z X = x)) E( Z X = x) = E(max Y
( − 50 0
; ) max Y
( − 50 0
; ) > max( X − 50 0
; )) P(max > max) +
1
4
4
4
4
4
4
4
4
4
4
4
4
2
4
4
4
4
4
4
4
4
4
4
4
4
3
A
,
1 5 x
1
+ max( X − 50 0
; ) P(max( X − 50 0
; ) ≥ max Y
( − 50 0
; )) =
( y
1
4
4
4
4
4
4
2
4
4
4
4
4
4
3
ò
− 50) dy + max( X − 50 0
; ) B
x max(50; x)
B
1
4
4
4
2
4
4
4
3
A
max 2 5
(
;
0 x)
50 max 5
(
;
0 x)
A = 1
,
1 25 x − 75 −
+
2 x
x
max 5
(
;
0 x)
B = P( Y ≤ max 5
(
;
0 x)) =
− 5
,
0
x
2
2
2
2
max 5
(
;
0 x)
E
= ò5050 1 250 5 70 −
=
ln
+
50
40
x
x 30
3
4
60
max 5
(
;
0 x)
E
= .....
x
é250 5 702 − 502 ù
é5 5 2ù 20
20
RAZEM : 1
,
1 25 ⋅ 55 − 75 − 5
,
0 ê
ln
+
ú + 50 ln +
+
− 5
,
0 ⋅
ê
ú
ë 3
4
60
û
ë3 4 3û
3
3
ì400000 = Pa 30;0,08
ïïí ZAD 1( )5 = Pa
→ do1 5 p
laci P
; o
d 1
6 d
o 3
0 2
P
15;0,08
ïïî Pa = Ra
15;0,08
15;0,08
N =
0
,
0 05 v a
P &
&
+ 0
,
0 05 ⋅ 9
,
0 95 2
v
a
P &
&
+ ... + 0
,
0 05 ⋅ 9
,
0 9514 15
v
a
P &
&
+
30
29
16
+ 0
,
0 05 ⋅ 9
,
0 9515 16
v ⋅ 2 a
P &
&
+ 0
,
0 05 ⋅ 9
,
0 9516 17
v
⋅ 2 a
P &
&
+ .... + 0
,
0 05 ⋅ 9
,
0 9529 30
v
⋅ 2 P =
15
14
1
30
− v
1
29
− v
− v
− v
14
1
16
14
15
15 1
15
= 0
,
0 05 P
+ 0
,
0 05 ⋅ 9
,
0 95 Pv
+ ... + 0
,
0 05 ⋅ 9
,
0 95 Pv
+ 0
,
0 05 ⋅ 9
,
0 95 ⋅ 2 Pv
+
i
i
i
i
0
,
0 05 ⋅ 9
,
0 9514
14
Pv
é 0
,
0 05
30
Pv
0
,
0 05 ⋅ 9
,
0 95
30
Pv
0
,
0 05 ⋅ 9
,
0 9514 30
v P ù
+
− ê
+
+ ... +
ú +
i
ë
i
i
i
û
0
,
0 05 ⋅ 9
,
0 9515 ⋅ 2
15
Pv
0
,
0 05 ⋅ 9
,
0 9516 ⋅ 2
16
Pv
0
,
0 05 ⋅ 9
,
0 9529 ⋅ 2
29
+
+
+
Pv
... +
−
i
i
i
é 0
,
0 05 ⋅ 9
,
0 9515 ⋅ 2
30
Pv
0
,
0 05 ⋅ 9
,
0 9516 ⋅ 2
30
Pv
0
,
0 05 ⋅ 9
,
0 9529 ⋅ 2
30
Pv
ù
− ê
+
+ ... +
ú =
ë
i
i
i
û
0
,
0 05 P 1 − ( 9
,
0 95 v)15
0
,
0 05
30
Pv
1 − 9
,
0 9515
0
,
0 05 ⋅ 9
,
0 9515 ⋅ 2
15
Pv
1 − ( 9
,
0 95 v)15
=
−
+
−
i
1 − 9
,
0 95 v
i
1 − 9
,
0 95
i
1 − 9
,
0 95 v
0
,
0 05 ⋅ 9
,
0 9515 ⋅ 2
30
Pv
1 − 9
,
0 9515
−
i
1 − 9
,
0 95
gdzie:
400000
P =
→≈ 37090
a 30;0,08
Zadanie 6
1.
−0 1
, 2
NPV =
⋅
Xe
−100
X~ rozkład
2
(
æ... . . .... ö
p ( )
2 ; p ( )
2 = ( p ; p )
1
2
)
1
2 ç
ç
÷÷
è... . . .....ø
é
2
,
0 4
6
,
0 ù
é ,
0 22
7
,
0
ù
8
ê
ú = ê
ú
ë 1
,
0
9
,
0 û
ë 1
,
0 3
8
,
0 7û
Z tego wynika:
p ( )
2 = ,
0 22 p + 1
,
0 3 p
1
1
2 p = 1− p
p ( )
2 =
7
,
0 8 p + 8
,
0 7 p
2
1
2
1
2
p ( )
2 =
0
,
0 9 p + 1
,
0 3
1
1
p ( )
2 = − 0
,
0 9 p + 8
,
0 7
2
1
EX = p ( )
2 ⋅ 215 + p ( )
2 ⋅100
1
2
EX = 21 (
5
0
,
0 9 p + 1
,
0
)
3 + 10 (
0 − 0
,
0 9 p + 8
,
0 7) = 10 3
, 5 p + 114 9
, 5
1
1
1
Z 1 mamy:
100 0,2
e
= 10 3
, 5 p + 114 9
, 5 → p ≈
6
,
0 9 ;
5 p = 1 − p ≈ 3
,
0 05
1
1
2
1
Zadanie 7
1
,
1 2− t −1
s
=
2− t
ln 1
,
1
æ 1 ln 1
,
1
ö
ODP = ex çç
p ò
−
dt
t
÷÷
è 0
2
1
,
1
−1 ø
1
,
1 x −1 = t
2 − t = x
ò
t
t
.... = t = 2 − x = ò2 ln 1, 1
ln 1
( +
dx = x =
)
= 0,21 1
1
1
,
0 21
1
,
1
0,21
ln
ln
x
0 1
,
1
ò
=
0 1
,
ò
⋅
−
=
=
1
,
1
−1
ln 1
,
1
t( t + )
1
t
t + 1
t + 1
,
1 21⋅
dt = −
1
,
0
dx
dx =
1
dt
ln
(
1
,
1 t + )
1
...
ò
,
0 21⋅ 1
,
1
ODP = e
=
≈ 9
,
1 1
,
1 21⋅ 1
,
0
Zadanie 8
Y ~ J (40 8
; 0)
Z-60 - zysk po roku
Z ~ J ( ,
0 7 Y
5
,
1
;
Y )
EZ − 60
1
,
1 Y − 60
600
=
= Y −
- cena kontraktu w zaleŜności od Y po 0,5 roku 1
,
1
1
,
1
11
cena wykonania o
pcji
æ
4
6
4
7
8
ö
ç
÷
600
600
maxç Y −
− k 0
;
÷ Y −
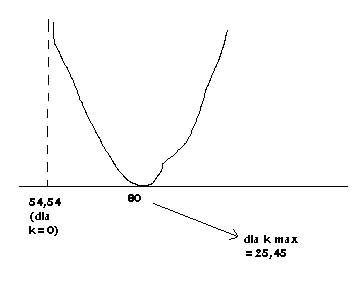
> K → K ≤ 2 , 5 45 (
dla Y
= 80 m
ax o
raz K
m
usi b
y
ć ≥ 0
11
11
çç
÷÷
è
ø
2
æ 600
ö
1 æ 600
ö
E max = 80 − 2ç
+ k ÷ +
ç
+ k ÷
è 11
ø 80 è 11
ø
600 + k = x (równanie kwadratowe) 11
stąd maksymalna cena dla k=0
600
6002 1
80 − 2 ⋅
+
11
112 80
ODP =
≈ 7 3
, 6
1
,
1
Zadanie 9
TO WYNIKA BEZPOŚREDNIO Z TEORII Zadanie 10
ZYSK = K = ò∞ 2 −0 1, t e
t dt = 2000
0
0
− ,2 x
X ~ ,
0 e
2
0
− ,5 y
Y ~
e
5
,
0
min(X,Y)=T
Z = −
e 0 T
1
,
K → trzeba obliczyć EZ
P(min( X , Y ) ≤ t) = 1− P(min ≥ t) = 1− P( X ≥ t) P( Y ≥ t) =
= 1
− 0,2 t − 0,5
− e
e
t = 1
− 0,7
− e
t → f (min) = 7
,
0
− 0,7
e
t t > 0
∞
∞
7
EZ ( bez k )
− 0 1
,
=
t
e
7
,
0
− 0,7 t
e
= 7
,
0
− 0,8 t
e
= ...
ò
ò
=
0
0
8
7
7
ODP =
K =
⋅ 2000 = 1750
8
8