Egzamin dla Aktuariuszy z 11 października 2003 r.
Matematyka Finansowa
Zadanie 1
(i)
NIE bo:
L=1 bo się skraca licznik i mianownik
1
)
(
1
−
=
−
=
i
i
P
(ii)
NIE bo:
n
m
n
n
n
n
v
a
P
v
a
s
)
(
&
&
&
&
&
&
=
=
)
(
)
(
)
(
)
(
)
(
)
1
(
)
1
(
m
n
n
m
n
m
n
n
n
m
n
n
m
a
a
m
i
i
i
P
v
i
a
v
i
a
m
i
i
i
v
a
m
i
i
i
L
&
&
&
&
&
&
=
úû
ù
êë
é
+
←
≠
+
=
+
úû
ù
êë
é
+
=
úû
ù
êë
é
+
=
(iii)
NIE bo:
1
)
1
ln(
−
−
=
≠
−
=
+
−
=
δ
δ
δ
e
P
L
i
L
bo:
...
4
3
2
)
1
ln(
...
!
2
!
1
1
4
3
2
2
+
−
+
−
=
+
+
+
+
=
x
x
x
x
x
x
x
e
x
Zadanie 2
(
)
max
)
2
4
3
(
)
1
4
3
(
2
4
2
3
3
2
2
3
2
1
3
2
→
−
−
+
+
−
+
+
−
+
α
α
α
v
v
v
v
v
v
v
przy warunku:
0
,
,
,
,
3
3
2
2
5
4
3
2
1
5
3
4
3
2
1
≥
=
+
=
+
+
+
α
α
α
α
α
α
α
α
α
α
α
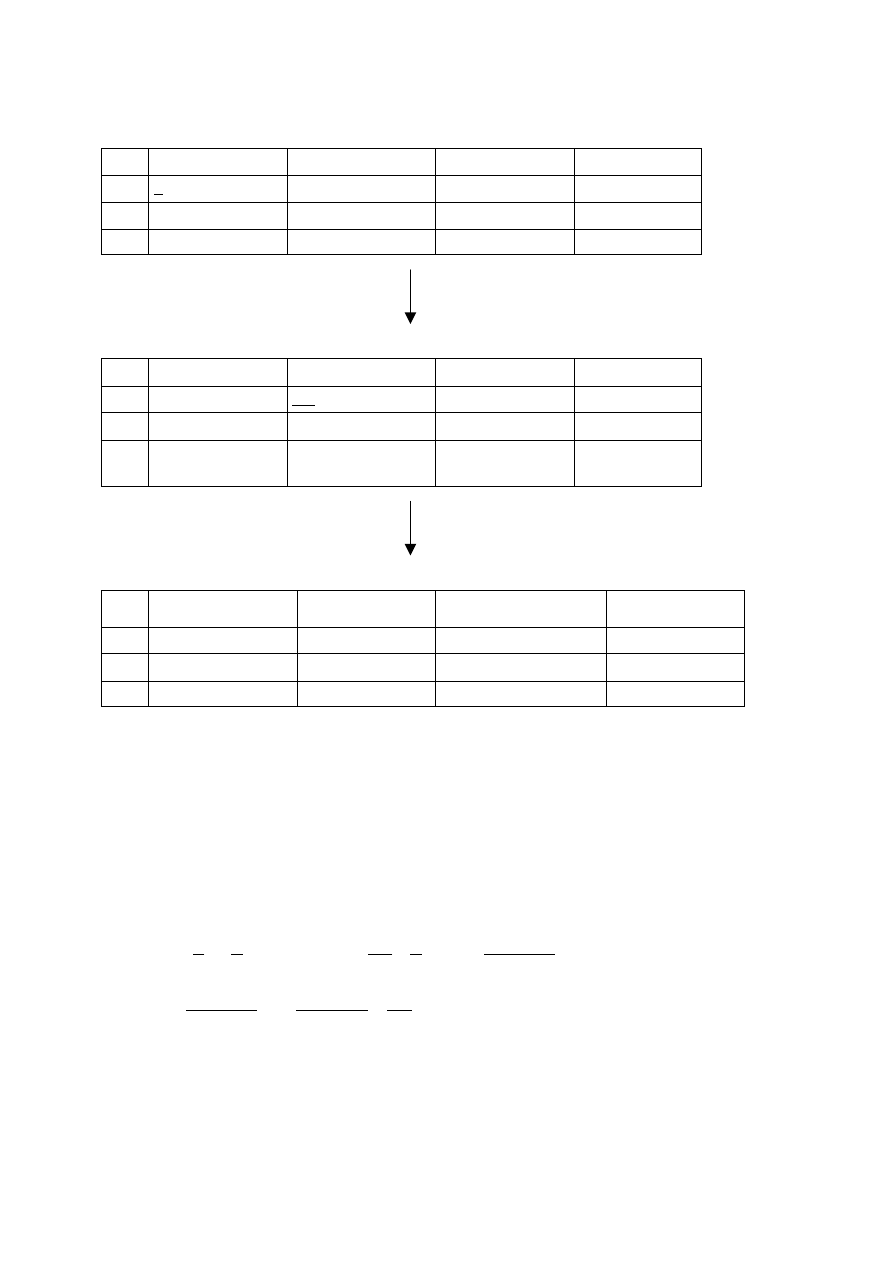
Rozwi
ą
zujemy to metod
ą
Sympleks:
1
α
2
α
3
α
4
α
2
1
2
3
5
α
0
0
1
3
2
4
2
3
2
−
+
v
v
1
4
3
3
2
−
+
v
v
v
v
v
−
−
+
2
4
3
3
2
0
4
α
2
α
3
α
1
α
0,5
0,5
1
1,5
5
α
0
0
1
3
0
1
2
3
2
<
+
−
−
v
v
0
2
2
3
2
>
+
v
v
0
2
<
−
v
v
3
6
3
3
2
+
−
−
v
v
4
α
1
α
3
α
2
α
1
2
2
3
5
α
0
0
1
3
0
1
4
3
3
2
<
+
−
−
v
v
0
4
4
3
2
>
−
−
v
v
0
4
3
3
2
<
−
−
−
v
v
v
...
3
6
3
3
2
+
−
−
v
v
........................
3
2
=
→
α
50
,
12
)
1
4
3
(
3
3
2
≈
−
+
=
v
v
ODP
Zadanie 3
Robimy zmian
ę
sumowania:
( )
(
)
åå
å
å
=
=
=
=
−
+
=
÷
ø
ö
ç
è
æ
+
=
÷
ø
ö
ç
è
æ
÷
ø
ö
ç
è
æ
÷÷
ø
ö
çç
è
æ
5
1
15
0
5
1
5
1
15
15
15
15
4
8
,
1
4
2
9
,
0
9
,
0
4
2
1
15
j
k
j
j
k
k
k
j
j
j
k
(
)
(
)
[ ]
å
å
=
=
≈
⋅
=
+
−
+
=
5
1
5
1
15
15
15
15
15
1894
....
4
1
4
4
,
1
4
8
,
1
j
j
j
j
ODP

Zadanie 4
Je
ś
li
[
]
[
]
7
,...,
0
)
1
(
10000
;
10000
∈
+
∈
k
k
k
X
i
To:
[
]
k
X
fix
X
fix
X
k
k
i
i
⋅
=
−
+
+
⋅
+
+
⋅
+
10000
)
(
gdzie
)
(
)(
1
(
10000
...
10000
2
10000
05
,
0
Z tego wynika:
úû
ù
êë
é
+
+
+
)
(
)
1
(
2
1
10000
05
,
0
i
X
X
X
X
fix
k
k
k
suma dla dwóch:
Y
X
i
i
i
Y
i
X
Y
Y
X
X
k
k
CONSTANT
Y
fix
X
fix
Y
fix
k
X
fix
k
k
k
k
k
,
ustalonych
przy
)
(
)
(
min
)
(
)
1
(
)
(
)
1
(
5000
5000
5000
5000
2
2
=
+
→
→
+
+
+
+
+
+
+
Z tego min gdy
→
+
+
−
<
+
=
2
2
2
2
)
1
(
)
1
(
a
a
a
a
k
k
Y
X
dzielimy kredyt na równe cz
ęś
ci
[
]
3
n
dla
min
nosci
nieskonczo
do
n
przy
rosnie
n
2000
8
n
17636
7
16090
6
14545
5
13000
4
12136
3
81
,
12181
1
,
1
7500
4
6
10000
2
05
,
0
2
2000
)
37500
(
2
45
,
14545
1
,
1
)
5000
8
28
10000
(
05
,
0
2000
1
=
→
⋅
≥
≈
=
≈
=
≈
=
≈
=
≈
=
≈
⋅
+
⋅
⋅
+
⋅
=
≈
⋅
+
⋅
+
=
dla
n
n
n
n
n
itd
n
n
Zadanie 5
2
1
15
0
1
,
0
2
2
20
0
07
,
0
2
1
R
R
ODP
dt
e
t
R
dt
e
t
R
t
t
−
=
=
=
ò
ò
−
−
ò
−
−
−
−
−
=
n
n
n
t
ne
e
n
dt
e
t
0
3
2
3
2
2
2
δ
δ
δ
δ
δ
δ
589
2
1
≈
−
R
R

Zadanie 6
Zało
ż
enie (face value) oznacza,
ż
e wykup w wysoko
ś
ci nominału
12=U(P1)d1+U(P2)d2+U(P3)d3
10
10
10
10
1
,
0
10
1
,
0
1
v
a
v
Ia
d
+
+
=
d2=20
11
1
3
=
+
=
=
∞
∞
i
i
a
Ia
d
)
3
(
)
2
(
50
,
15
11
)
3
(
)
2
(
)
3
(
20
)
3
(
)
2
(
)
2
(
.
1
P
U
P
U
P
U
P
U
P
U
P
U
P
U
P
U
=
→
=
+
+
+
2. U(P1)+U(P2)+U(P3)=1
Z 1 i 2 mamy:
2
)
1
(
1
)
3
(
)
2
(
P
U
P
U
P
U
−
=
=
%
40
1
5
,
5
10
5
,
3
)
1
(
2
))
1
(
1
(
11
2
)
1
(
1
20
1
)
1
(
12
≈
−
+
=
→
−
+
−
+
=
d
P
U
P
U
P
U
d
P
U
Zadanie 7
[
]
)
1
(
2000
)
2
1000
(
20000
2
1000
)
4
500
(
10000
1
5
5
5
10
10
v
v
a
P
K
v
a
P
K
+
−
+
+
=
−
+
+
=
- koszty calkowite
Jednostkowe takie same bo 10P - produkcja
Z tego wynika:
1770
2
1
≈
→
=
P
K
K
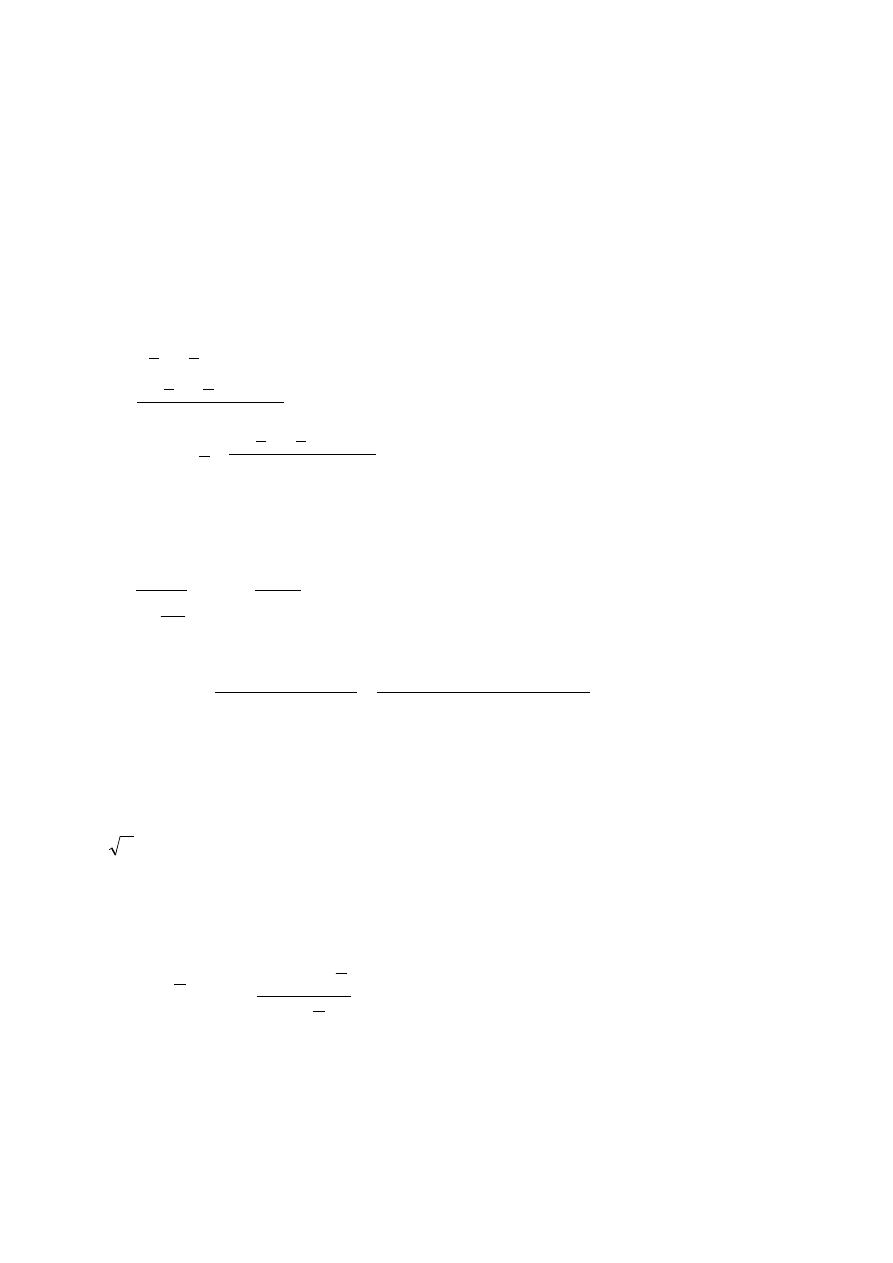
Zadanie 8
1
2
)
1
(
2
2
−
=
−
−
n
n
n
[
]
26
25
25
26
25
2
25
2
26
2
25
3
2
26
2
25
2
2
3
2
2
2
2
2
26
2
4
2
3
2
2
25
2
2
2
625
2
625
...
25
...
2
2
25
)
1
25
2
(
...
)
1
3
2
(
)
1
2
2
(
25
)
24
25
(
...
)
2
3
(
)
1
2
(
)
1
(
25
...
3
2
25
...
2
1
v
a
Ia
v
v
v
v
v
v
v
v
v
v
v
v
v
v
v
v
v
v
I
v
v
v
v
Iv
v
v
v
I
−
−
=
=
−
−
−
−
−
+
+
+
=
=
−
−
⋅
+
+
−
⋅
+
−
⋅
+
=
=
−
−
+
+
−
+
−
+
=
−
+
+
+
+
=
+
+
+
=
v
v
a
Ia
I
−
−
−
=
1
625
2
26
25
25
1615
1
625
2
26
26
25
25
25
≈
−
−
−
−
=
v
v
a
Ia
Ia
ODP
Zadanie 9
)
...
(
)
...
(
2
127
3
128
4
2
v
v
v
X
v
v
v
X
K
+
+
+
+
+
+
+
=
v
v
i
i
v
4
4
4
1
1
)
4
(
)
4
(
−
=
→
+
=
)
...
(
)
...
(
2
63
3
64
2
v
v
v
X
v
v
X
PD
+
+
+
+
+
+
=
2
129
130
2
2
65
66
2
1
8
,
0
8
,
0
6
,
1
6
,
1
1
2
2
8
,
0
v
v
v
v
v
v
v
v
v
v
K
PD
−
−
+
−
=
−
−
+
−
→
=
odpada
reszta
x
x
v
v
v
v
v
v
v
v
v
v
v
v
v
v
v
v
1
25
,
0
6
,
0
0
2
,
0
8
,
0
8
,
0
8
,
0
1
)
1
)(
2
1
(
8
,
0
)
1
)(
2
1
(
)
8
,
0
6
,
1
)(
1
(
)
2
)(
1
(
2
1
64
128
128
64
128
64
2
128
2
64
−
=
=
=
∆
=
+
−
−
=
−
−
+
=
−
+
+
−
=
+
−
x
v
=
64
%
80
,
8
25
,
0
25
,
0
4
4
25
,
0
64
1
64
1
)
4
(
64
1
1
≈
⋅
−
=
→
=
i
v

Zadanie 10
(
)
[
]
(
)
[
]
5
,
0
5
,
0
2
5
,
0
5
,
0
1
2
1
5
,
0
)
/(
/
ln
5
,
0
)
/(
/
ln
)
(
)
exp(
)
(
sT
sT
RT
X
P
d
sT
sT
RT
X
P
d
d
N
RT
X
d
N
P
P
S
S
S
C
−
+
=
+
+
=
−
−
=
S
P - cena akcji = 100
X=93,084
R=0,12
T=0,25
S=0,2
)
exp( RT
X
P
P
ODP
S
C
−
+
−
=
Wyliczamy i wychodzi około 0,79
Wyszukiwarka
Podobne podstrony:
2004 10 11 matematyka finansowaid 25165
2004.10.11 matematyka finansowa
2004 10 11 matematyka finansowaid 25165
Egzamin 2003.10.11, rozwiazania zadań aktuarialnych matematyka finansowa
mat fiz 2003 10 11 id 282349 Nieznany
1 2006 10 09 matematyka finansowaid 8919
2003.01.25 matematyka finansowa
2003.12.06 matematyka finansowa
1 2009 10 05 matematyka finansowaid 8924
2002 10 12 matematyka finansowaid 21647
2003 05 17 matematyka finansowaid 21697
2007.10.08 matematyka finansowa
2008.10.06 matematyka finansowa
1 2009.10.05 matematyka finansowa
2003.10.11 prawdopodobie stwo i statystyka
1 2006.10.09 matematyka finansowa
2010.10.04 matematyka finansowa
więcej podobnych podstron