Egzamin dla Aktuariuszy z 17 maja 2003 r.
Matematyka Finansowa
Zadanie 1
1
1
1
1
1
−
−
−
−
−
=
−
=
n
n
n
n
n
a
v
Ia
Ia
v
a
a
I.
98
,
9
8
,
0
04
,
0
8
,
0
04
,
0
⋅
=
+
=
+
n
n
n
n
nXv
Ia
Xv
a
Po roku :
v
v
v
v
Xv
a
v
Xv
v
v
a
Xv
a
n
n
n
n
n
n
04
,
0
8
,
0
04
,
0
04
,
0
04
,
0
04
,
0
1
1
−
=
−
+
=
+
÷
ø
ö
ç
è
æ
−
=
+
−
−
[
]
v
v
v
Xv
a
nXv
Ia
v
Xv
v
nXv
v
a
v
Ia
v
Xv
n
Ia
n
n
n
n
n
n
n
n
n
n
98
,
8
8
,
0
8
,
0
98
,
9
8
,
0
)
04
,
0
(
04
,
0
)
(
04
,
0
)
1
(
04
,
0
1
1
⋅
=
−
⋅
=
+
−
+
=
=
−
+
−
−
−
=
−
+
−
−
Analogicznie dla drugiej obligacji:
udzial
to
0,4
gdzie
4
,
0
04
,
0
8
,
0
04
,
0
8
,
0
98
,
8
8
,
0
⋅
−
=
−
⋅
=
v
v
C
v
d
A
A
6
,
0
06
,
0
9
,
0
06
,
0
9
,
0
85
,
7
9
,
0
⋅
−
=
−
⋅
=
v
v
C
v
d
B
B
052
,
0
06
,
0
6
,
0
04
,
0
4
,
0
2
=
⋅
−
⋅
=
=
C
c
C
d
35
,
8
≈
+
+
+
+
=
C
B
A
C
C
B
B
A
A
C
C
C
C
d
C
d
C
d
ODP
Zadanie 2
od - odchylenie stopy zwrotu akcji
[
]
[
]
5
,
0
5
,
0
2
5
,
0
5
,
0
1
2
1
5
,
0
)
/(
)
/
ln(
5
,
0
)
/(
)
/
ln(
)
exp(
)
(
)
exp(
)
(
n
od
n
od
Rn
E
S
d
n
od
n
od
Rn
E
S
d
Rn
E
S
C
P
d
N
Rn
E
d
SN
C
E
E
E
⋅
−
⋅
+
=
⋅
+
⋅
+
=
−
+
−
=
−
−
=
(i)
0
R
n
)
exp(
)
(
)
exp(
)
(
)
(
)
exp(
)
(
2
1
2
1
=
→
∀
−
+
−
−
−
=
−
−
Rn
S
S
d
N
Rn
S
d
SN
d
N
Rn
S
d
SN
(ii)
X
n
od
SN
n
od
SN
X
d
N
Rn
S
d
SN
n
n
dla
=
⋅
−
−
⋅
→
=
−
−
=
)
5
,
0
(
)
5
,
0
(
)
(
)
exp(
)
(
5
,
0
0
5
,
0
0
2
0
1
0

(
) (
)
[
]
X
odn
N
odn
N
S
n
od
SN
n
od
SN
ODP
2
5
,
0
5
,
0
2
)
)
4
(
2
1
5
,
0
(
2
)
)
4
(
2
1
5
,
0
(
2
5
,
0
0
5
,
0
0
5
,
0
5
,
0
=
−
−
=
=
⋅
−
−
⋅
=
Zadanie 3
)
20
(
14
,
0
25
,
0
14
,
1
)
10
(
14
,
0
;
10
10
dlug
Ls
L
dlug
=
⋅
−
⋅
=
(i)
10
1
,
0
;
10
10
1
,
1
5
,
0
1
,
1
)
20
(
⋅
+
=
+
⋅
L
Xa
NPV
L
dlug
L
od
å
=
⋅
−
⋅
⋅
=
úû
ù
êë
é
⋅
−
−
⋅
=
10
1
08
,
0
;
10
08
,
0
;
10
10
08
,
0
5
,
0
08
,
0
5
,
0
1
,
1
08
,
1
08
,
0
10
5
,
0
)
1
(
5
,
0
k
k
od
Ia
a
L
k
L
NPV
Wiemy,
ż
e:
obliczamy
1
,
1
5
,
0
450000
1
,
1
)
20
(
12
,
0
5
,
0
12
,
1
14
,
0
5
,
0
12
,
1
14
,
1
)
20
(
10
1
,
0
;
10
10
*
12
,
0
;
10
10
14
,
0
;
10
10
10
*
L
L
a
NPV
L
dlug
Ls
Ls
L
dlug
od
→
⋅
+
=
=
⋅
−
⋅
⋅
−
⋅
⋅
=
Z (i) wychodzi X około 213046
Zadanie 4
)
1
(
...
2
)
3
2
(
)
1
(
...
2
1
...
...
3
2
)
3
2
(
2
)
1
(
...
2
1
2
)
3
2
(
)
1
(
...
2
1
)
1
(
...
2
1
...
...
2
1
1
1
2
3
2
1
2
1
+
+
+
+
+
+
+
−
+
+
+
+
=
+
+
+
+
+
−
+
+
+
+
=
+
+
+
−
+
+
+
+
=
+
+
+
+
=
+
=
=
+
+
+
+
n
n
n
n
n
n
r
n
n
n
n
r
n
n
n
r
n
r
r
r
n
n
n
n
{
}
)
1
2
(
2
2
)
3
2
)(
1
(
2
1
1
n
1,...,
k
2
)
1
(
+
−
−
+
+
+
+
−
−
−
+
=
+
∈
+
=
→
n
k
k
n
n
n
k
n
n
r
k
k
r
k
k
Analizuj
ą
c dochodzimy do tego,
ż
e max dla k=n+1 bo:
1
n
k
dla
+
≤
k
r
jest funkcj
ą
rosn
ą
c
ą
wi
ę
c max dla k=n+1
k
r dla k>=n+2 jest parabol
ą
i wierzchołek jest w k wi
ę
kszym od n+1, dlatego max dla k=n+2
Porównuj
ą
c warto
ś
ci dla k=n+1 i k=n+2 otrzymujemy,
ż
e max dla k=n+1
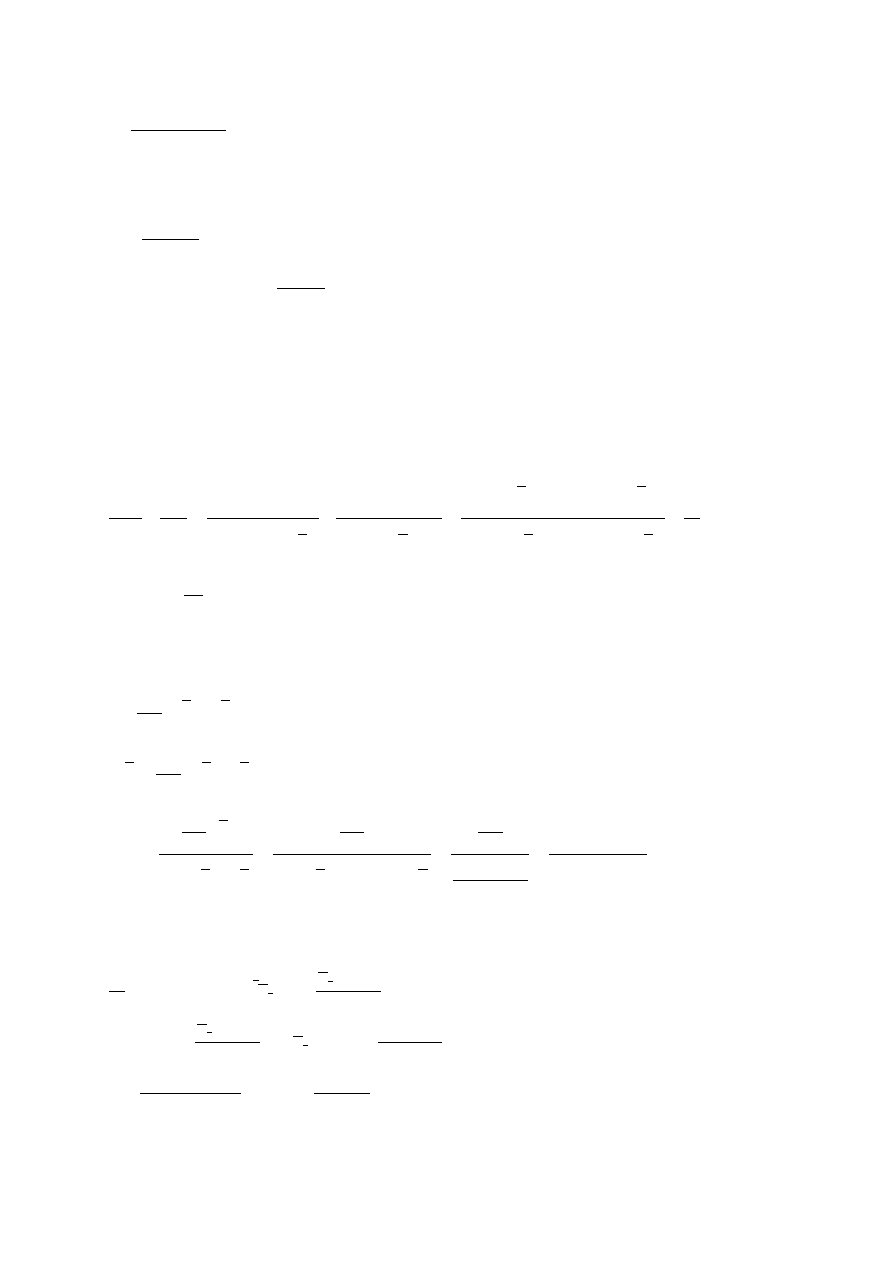
38
780
2
)
2
)(
1
(
=
→
=
+
+
→
n
n
n
Czyli:
{
}
{
}
77
,...,
40
)
39
(
2
40
79
)
39
(
780
39
,...,
1
2
)
1
(
∈
−
+
+
−
−
=
∈
+
=
k
dla
k
k
k
r
k
dla
k
k
r
k
k
51
,
99
36
171
406
741
465
210
55
2
1
70
60
50
40
30
20
10
70
60
50
40
30
20
10
≈
+
+
+
+
+
+
=
=
+
+
+
+
+
+
=
−
v
v
v
v
v
v
v
r
r
r
r
r
r
r
R
R
Zadanie 5
(i)
TAK bo:
( )
( )
( )
( )
( )
( )
å
∞
=
−
−
−
−
=
+
=
−
=
úû
ù
êë
é
+
+
−
−
+
úû
ù
êë
é
+
+
−
−
+
=
úû
ù
êë
é
−
+
−
úû
ù
êë
é
+
−
=
−
1
1
1
1
1
1
1
1
)
(
)
(
(Taylor)
)
1
ln(
)
1
(
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
m
m
m
m
m
m
m
m
m
m
m
i
m
i
m
i
i
m
i
i
i
m
i
m
i
d
δ
(ii)
TAK bo:
÷
÷
ø
ö
ç
ç
è
æ
+
+
=
÷
÷
ø
ö
ç
ç
è
æ
+
+
=
...
1
...
1
3
2
2
1
2
1
2
m
m
m
m
m
v
v
m
Iv
v
v
m
I
(
)
)
(
)
(
)
(
)
(
2
1
1
2
2
1
1
2
1
1
)
1
(
2
)
1
(
1
2
1
1
m
m
m
m
m
m
m
m
m
d
i
m
m
d
i
m
i
i
m
v
v
v
m
I
−
=
−
=
+
+
−
+
=
+
−
=
→
−
(iii)
TAK bo:
( )
(
)
1
1
1
1
1
0
1
1
)
1
(
)
1
(
+
+
+
+
+
−
−
−
=
−
+
−
−
=
−
−
=
−
=
−
−
−
=
−
−
=
−
=
+
∂
∂
ò
n
n
n
n
n
n
n
n
n
n
n
n
n
n
t
nv
v
v
nv
v
v
P
nv
v
v
nv
a
v
nv
a
v
L
nv
a
v
a
I
v
dt
i
i
δ
δ
δ
δ
δ
δ
Zadanie 6
α
α
α
8
)
...
(
...
...
2
)
(
12
5
8
6
5
2
5
1
=
+
+
=
+
=
v
v
X
v
v
X
v
X
)
(
)
(
6
5
4
3
4
3
2
2
1
v
v
v
X
v
v
X
v
X
ODP
+
+
+
+
+
=
Wiemy,
ż
e:
obliczamy
370
)
1
(
8
)
1
(
7
370
)
1
(
)
1
(
3
8
4
7
4
3
8
7
α
α
α
→
=
−
+
−
=
−
+
−
v
a
v
v
a
v
v
X
v
X
34
,
5733
07
,
1
3
07
,
1
2
07
,
1
3
2
2
3
3
3
3
4
2
2
2
4
2
5
≈
+
+
⋅
=
+
+
=
α
α
α
α
α
α
a
v
a
v
a
v
a
v
v
v
ODP
Zadanie 7
........
).........
12
,
1
1000
5
,
0
12
,
1
1000
(
5
,
0
12
,
1
1000
5
,
0
:
....
..........
12
,
1
)
12
,
1
1000
5
,
0
1000
(
12
,
1
1000
2
⋅
⋅
+
⋅
⋅
⋅
⋅
⋅
+
⋅
WYP
K
[
]
[
]
(
)
(
)
å
=
−
−
−
⋅
−
=
⋅
−
⋅
−
⋅
⋅
=
⋅
=
=
+
+
⋅
+
⋅
=
=
⋅
⋅
+
+
⋅
⋅
+
⋅
=
k
n
k
k
n
n
k
k
k
k
k
W
1
1
1
2
1
2
12
,
1
5
,
0
1
44
,
0
560
12
,
1
5
,
0
1
)
12
,
1
5
,
0
(
1
)
12
,
1
5
,
0
(
5
,
0
1000
5
,
0
5
,
0
12
,
1
1000
5
,
0
12
,
1
5
,
0
...
12
,
1
5
,
0
12
,
1
1000
5
,
0
12
,
1
1000
5
,
0
...
12
,
1
1000
5
,
0
12
,
1
1000
5
,
0
)
(
(
)
(
)
å
=
≈
ú
û
ù
ê
ë
é
⋅
−
⋅
−
⋅
−
=
=
20
6
15
6
19000
12
,
1
5
,
0
1
12
,
1
5
,
0
1
12
,
1
5
,
0
15
44
,
0
560
)
(
k
k
W
ODP
Zadanie 8
02
,
1
1
=
v
....
)
1
)(
(
)
(
)
1
(
3000
...
3000
)
(
)
3000
3000
(
...
6000
3000
100000
2
2
2
2
2
2
2
4
2
=
−
+
+
+
=
+
+
+
+
=
+
+
v
n
A
n
A
v
v
n
v
n
A
v
n
v
v
n
n
2
4
2
2
2
2
2
2
1
)
1
(
3000
)
1
(
1
3000
)
(
v
v
n
v
v
v
n
A
n
n
−
+
−
−
−
=
+
+
Porównujemy A(n) i 100000
Sprawdzamy,
ż
e dla n=7 A(n)<100000, dla n=8 A(n)>100000
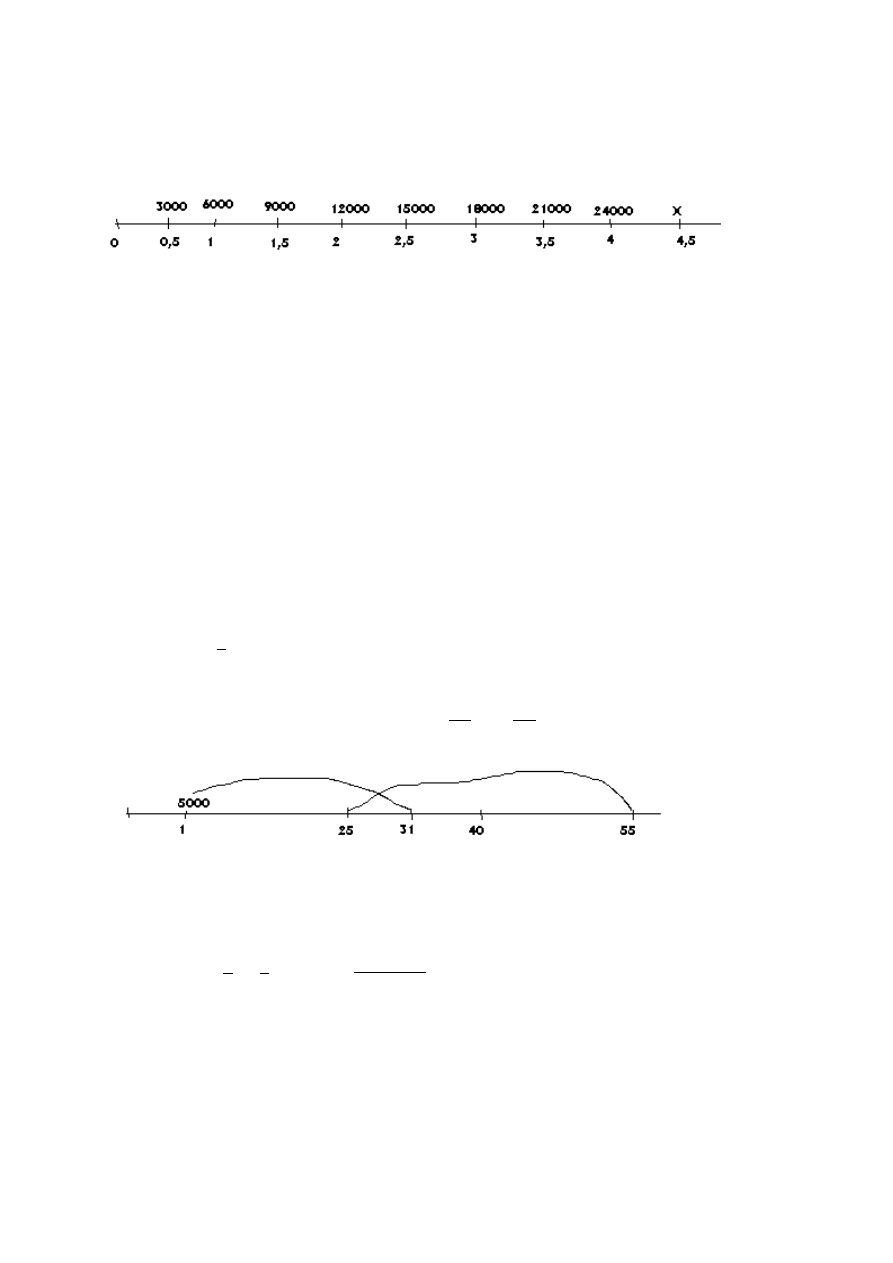
Z tego wynika:
obliczamy
8
3000
...
6000
3000
100000
18
16
4
2
X
Xv
v
v
v
→
+
⋅
+
+
+
=
0
)
5
,
4
(
)
4
(
24000
)
5
,
3
(
24000
21000
)
3
(
2
4
2
6
4
2
=
=
+
=
+
+
=
ZAD
Xv
ZAD
Xv
v
ZAD
Xv
v
v
ZAD
ZAD(3)-ZAD(3,5)=KAP(3,5)
ZAD(3,5)-ZAD(4)=KAP(4)
2
6
4
2
24000
21000
45000
)
4
(
24000
)
5
,
3
(
21000
Xv
Xv
v
v
KAP
KAP
ODP
+
−
−
−
=
−
+
−
=
Wychodzi około 4050.
Zadanie 9
(i)
30
5000
Xa
=
dla pojedynczej renty:
)
1
(
)
(
)
1
(
)
(
31
30
31
k
k
k
v
X
Xa
Xa
X
k
ZAD
k
ZAD
X
k
OD
−
−
−
−
=
+
−
=
+
−
−
=
(
)
[
]
(
)
ú
û
ù
ê
ë
é
−
−
=
−
−
=
=
−
=
+
+
+
=
å
=
−
14
30
30
14
30
31
30
15
31
12
,
1
12
,
1
12
,
0
12
,
1
1
16
16
)
1
(
)
15
(
...
)
29
(
)
30
(
X
s
s
v
X
v
X
OD
OD
OD
ODP
k
k
&
&
&
&
W stawiamy X wyliczony w równaniu (i) i wychodzi około 5603

Zadanie 10
ò
+
+
=
+
+
n
cn
bn
an
ct
bt
a
0
3
2
2
3
2
)
3
2
exp(
)
(
3
2
cn
bn
an
n
A
−
−
−
=
03
,
0
,
02
,
0
,
02
,
0
6
,
1
3
125
2
25
5
42
,
0
9
2
9
3
04
,
0
3
2
−
=
−
=
−
=
→
ï
ï
ï
î
ï
ï
ï
í
ì
=
−
−
−
=
−
−
−
=
−
−
−
c
b
a
c
b
a
c
b
a
c
b
a
58
3
343
2
49
7
exp
)
7
(
≈
÷
ø
ö
ç
è
æ
−
−
−
=
c
b
a
A
Wyszukiwarka
Podobne podstrony:
Egzamin 2003.05.17, rozwiazania zadań aktuarialnych matematyka finansowa
2003.05.17 prawdopodobie stwo i statystyka
2003.01.25 matematyka finansowa
2003.12.06 matematyka finansowa
2003 05 17 prawdopodobie stwo i statystykaid 21698
2008 03 17 matematyka finansowaid 26447
2010.05.31 matematyka finansowa
2005 05 16 matematyka finansowaid 25340
mat fiz 2003 05 17
1 2010 05 31 matematyka finansowaid 8925
2008.03.17 matematyka finansowa
1 2000 06 17 matematyka finansowaid 8918
2005.05.16 matematyka finansowa
2003 10 11 matematyka finansowaid 21704
2005 01 17 matematyka finansowaid 25337
2007 05 14 matematyka finansowaid 25650
2003 05 17 pra
więcej podobnych podstron