Egzamin dla Aktuariuszy z 16 maja 2005 r.
Matematyka Finansowa
Zadanie 1
k − kursUSD ~ λ( )
4
1
æ
P ö
ç1−
÷ - środki własne zaangaŜowane
è
100 ø
P ⋅ ,
0 05
zwrot: 1
( + R) −
k var( R) = 5
,
0
400
1
0
,
1 5 P
1 + R −
k 1
stopa zwrotu B:
400
−1
P
1 − 100
var wukl.
é
2
2
ù
}
1
P
0
,
1 5
5
,
0 ⋅ 4 =
ê 5
,
0 +
⋅ 16 ú → 1
,
1 025 2
p − 400 p + 15000 = 0 → p ≈ 42
2
æ
P ö ê
4002
ë
úû
ç1−
÷
è
100 ø
lub p>100 co niemoŜliwe
Zadanie 2
3
n − ( n − )
1 3 = 3 2
n − 3 n + 1
2
n − ( n − )
1 2 = 2 n −1
I = 13 + 23 v + 33 2
v + ...
Iv = 13 v + 23 2
v + ...
I 1
( − v) = 13 + 3
( ⋅ 22 − 3 ⋅ 2 + )
1 v + 3
( ⋅ 32 − 3 ⋅ 3 + )
1 2
v + ... =
= 1
(
3 2 + 22 v + 32 2
v + ...) − 2 − (
3 2 v + 3 2
v + ...)
2
+ v + v + ... =
= 1
(
3 2 + 22 v + 32 2
v + ...) − 1
(
3 + 2 v + 3 2
v + ...) + 1
2
+ v + v + ...
1
4
4
4
2
4
4
4
3
A
Av = 12 v + 22 2
v + ...
A 1
( − v) = 12 + (2 ⋅ 2 − )
1 v + (2 ⋅ 3 − )
1 2
v + ... = 2 1
( + 2 v + 3 2
v + ...) −1
2
− v − v − ...
1
4
4
4
2
4
4
4
3
B
2
Bv = v + 2 v + ...
1
2
B 1
( − v) = 1 + v + v + ... → B =
2
1
( − v)
2
1
1
(
3 + v)
3
1
−
−
+
1
( − v)2
1 − v
1 + v
1
( − v)3
1
( − v)2
1 −
A =
=
→ I =
v ≈ 79981
1 − v
1
( − v)3
1 − v
Bierze kredyt, wpłaca na depozyt: arbitraŜ gdy depozyt po roku większy od kredytu po roku ZałoŜenie: inwest.1 w PLN
Jest 6 moŜliwości (oczywiście bierzemy tylko pod uwagę w róŜnych walutach) 1
2
3
4
5
6
Kredyt:
PLN PLN EUR EUR USD USD
Dep:
EUR USD PLN USD PLN EUR
1. kredyt 1,1-PLN
dep: 0,2*1,03-EUR A)1,0918 E) 1,03
2. KREDYT: 1,1-PLN
DEP: 0,25*1,02-USD B(1,09395)
3. KREDYT: 0,2*1,06-EUR A) 1,1236 E) 1,06
DEP: 1,05-PLN
4. KREDYT: 0,2*1,06-EUR
DEP: 0,25*1,02-USD C)0,202725 D) 0,21428 EUR z tego wynika D) przy kursie 5. KREDYT: 0,25*1,04-USD
DEP: 1,05-PLN
6. KREDYT: 0,25*1,04-USD
DEP: 0,2*1,03-EUR
Zadanie 4
R ~ J (− ,
0
)
5
,
0
;
2
A
R ~ WYK (
)
1
,
0
0
P[47 1
(
5
,
+ R )
A
+ 4 ,
7
1
(
4 + R )
P R
R
0
≥ 100]
é
5 ù
= ê A + 0 ≥
ú
ë
47 5
, û
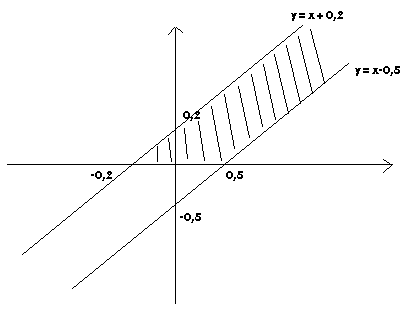
Znajdujemy rozkład R
: ( )
(
)
( )
A + R
g u
0
= ò∞ g u
1
− y g y dy
−∞
2
x ∈ (− ,
0 ;
2 ∞)
∞
1
g( x) =
χ
( x
ò
− y) ⋅1 e 1−0 y ( y) 0
χ
dy
( 0
− ,2;0,5]
(0;∞)
−∞
7
,
0
dl
a x ∈ (-0,2;0,5
) g
(x) = òx+0,2 1
−
10
10
10
y
e
dy =
[ −10( x+
1 −
0,2)
e
]
0
0,7
7
x
dl
a x ≥ 0,
5 g( x) = ò + 0,2 1
−
10
10
10
y
e
dy =
[ −10( x−0,5) −10( x+
e
−
0,2)
e
]
x − 0,5
7
,
0
7
5
é æ
5
10(
0,2)
öù
æ 5 ö
ODP = 1 − Fç
÷ =1− ò 10
x
10
5
47,5
[ −10( +
1 −
0,2)
e
]
−
+
dx = 1 − ê
ç
47,5
÷
+ 1
,
0 e
+ ,
0 2 − 1
,
0
ú ≈ 7 %
0
−
è 47 5
, ø
0,2 7
ê ç
÷
7
47 5
,
ú
ë è
øû
Zadanie 5
A - depozyt
B - WWW
C - ZZZ
A+B+C=1000000
Jak oba indeksy maleją lub tylko w to LOK=1000000
1000000
WYP : A ⋅ 1
,
1 2 ≥ 1000000 → A =
bo wyŜej zaleŜy bardziej od indeksów
1
,
1 2
1
B + C = 1000000 1
( −
)
1
,
1 2
1. oba indeksy rosną i w bardziej od z æ ind( )
w − 2000
ind ( z) − 24000 ö
1000000 k ⋅ maxç ;
0
−
÷ ≤
è
2000
24000
ø
B
æ ind( )
w − 2000 ö
C ⋅ 2400 æ ind ( z) − 2400 ö 200 ç
0
÷ +
ç
÷
250
è
2000
ø
2000 è
2400
ø
Z tego wynika: max gdy %w=%z
2. indeks w rośnie, z maleje
ind ( )
w − 2000
B
1000000 k
≤
( ind( )
w − 2000)
2000
250
B ⋅ 2000 ind ( )
w − 2000
C ⋅ 24000 ind ( )
w − 2000
1. 0 ≤
+
→ 8 B +12 C ≥ 0
250
2000
2000
2000
B
2.
≥ 500 k
250
1
B + C = 1000000 1
( −
)
1
,
1 2
znaleźć przecięcie:
8
C = −
B
12
1
B + C = 1000000 1
( −
)
1
,
1 2
I wstawić do nierówności 2, z tego wychodzi k=2,56
Zadanie 6
Tu jest chyba błąd:
Tylko (iii) prawdziwe bo:
NPV t
( ) = S t
( ) − ò∞
−δ ( s− t
k( s) e
) ds = S t
( ) −
t
δ ( s t)
δ ( s t
k( s) e
ds
k( s) e
) ds
t
ò∞
−
−
+
0
ò
−
−
0
NIE
N V
P ′( t) = S ′( t) − δ eδ t ò∞
−
k( s) e δ s ds + k( t) = 0
0
(iii)
TAK:
−
NPV t
( ) =
0 t
20 e
0
1
,
− ò∞ −0 s 1, −0,2( s− t 6 e
0
e
) ds = 0
t
Analogicznie (ii) NIE
Zadanie 7
I po rozpisaniu: 3,3,3,6,6,6,9,9,9,.....
v
− v
v
4
7
2
3
1
3
3
I = 3
( v + 6 v + 9 v + ... 1
( + v + v ) =
=
1
4
4
4
2
4
4
4
3
1
(
3
− v )2 1− v
1
(
3
− v ) 1
( − v)
A
3
4
7
10
Av = 3 v + 6 v + 9 v + ...
3 v
3
4
A 1
( − v ) = 3 v + 3 v + ... =
3
1 − v
é 1,
1
1
,
1 2
ù
é 1
1
1
2
ù
Π
II. 100ê
+
+ ...ú = 100
+
+
+ ... = 100
ê
ú
ë12 1
,
1
22 1
,
1 2
û
ë12
22
32
û
6
I + II ≈ 285
Zadanie 8
(i)
TAK:
max( ;
0 x − K ) − 2 max( ;
0 x − K ) + max( ;
0 x − K )
1
2
3
(ii)
NIE
max( ;
0 K − x) − 2 max( ;
0 K − x) + max( ;
0 K − x)
1
2
3
(iii)
NIE
max( ;
0 K − x) − 2 max( ;
0 x − K ) + max( ;
0 K − x)
1
2
3
(iv)
NIE
max( ;
0 x − K ) − 2 max( ;
0 K − x) + max( ;
0 x − K )
1
2
3
i sprawdzamy w przedziałach
t
a ( t) = exp( δ ( s) ds) ò
2
2
0
a ( n + )
1
ODP : 2
−1
a ( n)
2
1
1
a t
( )
exp( δ ( ) )
1
(
)
δ ( ) ln 1
(
)
1
=
ò t
−
s ds
1
= +
t
t
→
1
0
ò t
−
s =
+
t
t
0
d é 1
ù
1
1
δ ( t) =
− ln 1
( + t) =
ln 1
( + t) −
dąŜy do zera na mocy Hospitala
1
ê
ú
2
dt ë t
û t
t( t + )
1
Z tego wynika: α = 0
t
2 + 1
δ t()
2
= t 2 + t
ò tδ ( s) = ln( s 2 ) 2
+ s
0
a ( n
n 1
+
n
n
+ )
1
1
æ +
ö
æ n + 2 ö n + 2
2
= exp(
δ ( s)
ò
− δ ( s))
ò
= expç
δ ( s)÷
ò
= expçln
÷ =
a ( n
2
2
2
0
0
è n
)
ø
è
n ø
n
2
n + 2
n
2
ODP =
− =
n
n
n
Zadanie 10
Stopa jest mniejsza od 0,05 bo dla 0,05 byłoby 1000
50 1
(
100
− v )
f ( i) =
+1000 100
v
−1100
i
4900
ODP =
b
o iX = 100 ⋅ 50 + 1000 −1100
i
Numerycznie sprawdzając moŜna zawęzić do 110100