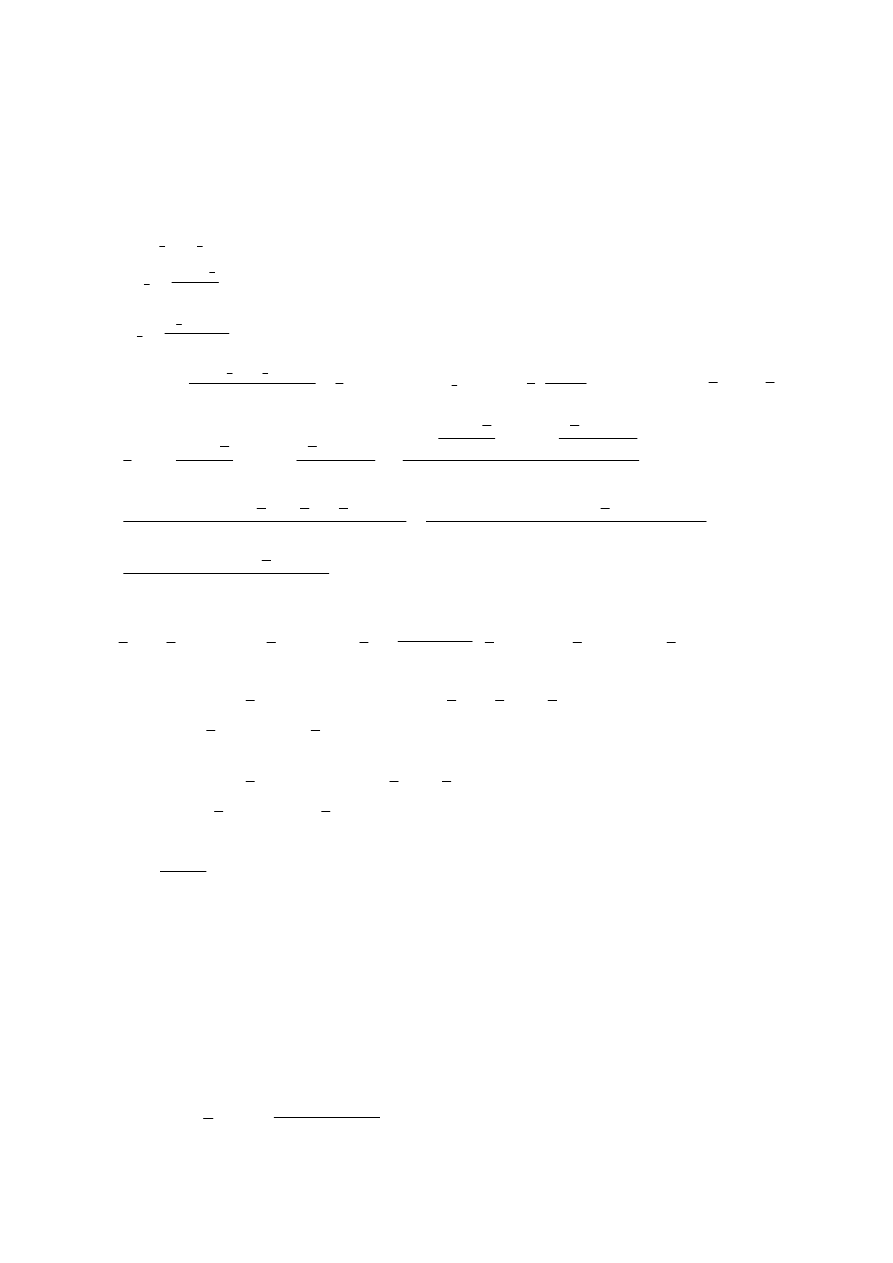
Egzamin dla Aktuariuszy z 5 października 2009 r.
Matematyka Finansowa
Zadanie 1
n
n
a
a
i
&
&
=
+
)
1
(
( )
( )
i
nv
a
Ia
i
a
n
Da
n
n
n
n
n
−
=
−
=
&
&
[
]
( ) ( )
∑
∑
=
=
=
+
+
−
⋅
+
=
+
+
−
=
+
−
−
=
−
10
1
10
1
10
10
)
2
(
10
2
10
1
1
)
2
(
1
n
n
n
n
n
n
n
Ia
Da
i
i
nv
a
i
n
i
i
nv
a
a
n
I
D
&
&
=
−
+
+
−
−
=
−
+
+
−
−
=
i
i
v
a
i
i
a
i
v
a
i
i
a
i
10
10
10
10
10
10
10
)
2
(
10
55
10
)
2
(
10
55
1
&
&
&
&
=
−
−
+
+
+
+
−
=
−
+
+
+
−
−
=
2
10
10
2
10
10
10
10
10
10
)
1
2
(
20
55
10
2
10
20
55
i
i
v
a
i
i
i
i
v
a
ia
a
i
i
→
−
+
+
−
=
2
10
10
10
)
2
3
(
20
45
i
v
a
i
i
(ii) TAK
sprawdzamy (i)
→
+
≠
+
=
+
+
+
=
+
=
+
→
=
10
10
10
10
10
10
10
)
1
2
(
)
2
(
1
)
1
(
2
1
)
2
3
(
)
2
3
(
a
v
a
v
a
i
i
v
a
i
a
i
a
v
a
&
&
&
&
&
&
&
&
&
&
(i) NIE
sprawdzamy (iii)
=
+
−
+
+
+
−
−
=
−
+
+
−
10
10
10
10
10
10
10
10
20
2
2
10
10
45
10
)
2
3
(
20
45
v
v
ia
a
a
i
v
a
i
i
→
−
+
+
−
+
−
=
10
10
2
20
10
45
10
10
10
10
v
a
v
a
i
&
&
(iii) NIE
sprawdzamy (iv)
=
−
−
+
−
+
+
=
−
+
+
−
2
18
2
12
2
3
45
10
)
2
3
(
20
45
10
10
10
10
10
10
v
v
ia
a
i
v
a
i
i
4
4 3
4
4 2
1
X
v
ia
v
a
i
2
2
2
12
3
18
45
10
10
10
10
−
+
+
−
+
−
=
→
=
−
+
−
=
−
+
−
=
0
2
2
2
2
2
2
1
2
10
10
10
10
v
v
v
i
v
i
X
(iv) TAK
czyli odpowiedź D jest prawidłowa
Zadanie 2
i=3,5%
zysk w k-tym roku:
(
)
1,2,...,25
k
dla
0
;
max
)
1
(
)
(
=
−
⋅
−
=
i
i
k
REZ
k
ZYSK
k
k
i - stopa zwrotu w k-tym roku
25
25
1
035
,
0
200000
200000
v
R
Ra
−
⋅
=
→
=
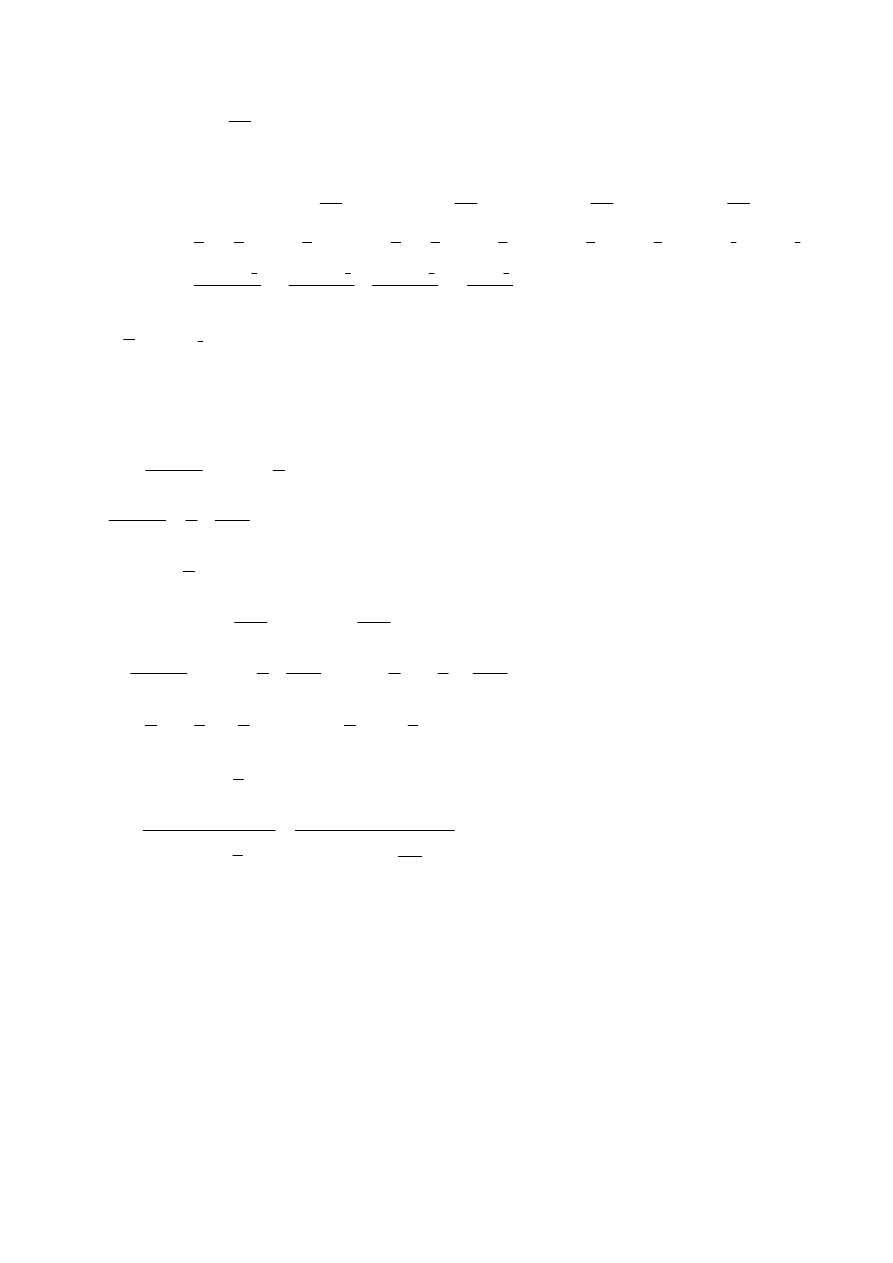
k
Ra
k
REZ
−
=
−
26
)
1
(
Całkowity zysk:
∑
∑
∑
∑
∑
=
=
=
=
=
−
−
−
−
=
⋅
+
⋅
+
⋅
+
⋅
=
=
25
1
5
1
10
6
15
11
25
21
26
26
26
26
01
,
0
005
,
0
015
,
0
025
,
0
)
(
k
k
k
k
k
k
k
k
k
Ra
Ra
Ra
Ra
k
ZYSK
ZYSK
(
)
(
)
(
)
(
)
[
]
=
+
+
+
+
+
+
+
+
+
+
+
+
+
=
1
5
11
15
16
19
20
21
24
25
...
01
,
0
...
005
,
0
...
015
,
0
...
025
,
0
a
a
a
a
a
a
a
a
a
a
R
=
−
+
−
+
−
+
−
=
i
a
i
a
v
i
a
v
i
a
v
R
5
5
10
5
15
5
20
5
2
5
5
3
5
5
005
,
0
(
)
[
]
2
3
5
55
7
1
10
15
20
5
+
+
+
−
=
v
v
v
a
R
36413
%
90
≈
⋅
=
ZYSK
ODP
Zadanie 3
∑
∑
∞
=
∞
=
=
+
1
1
1
2
)
1
(
1
k
k
k
k
v
k
v
k
k
N
1
1
1
)
1
(
1
+
−
=
+
k
k
k
k
∑
∞
=
=
1
1
)
(
k
k
v
k
v
f
∑
∫
∞
=
−
=
=
→
=
+
−
−
=
−
=
→
−
=
=
′
1
1
v)
-
-ln(1
f(v)
i
0
C
0
f(0)
ale
)
1
ln(
1
1
)
(
1
1
)
(
k
k
C
v
v
v
f
v
v
v
f
∑
∑
∑
∑
∞
=
∞
=
∞
=
∞
=
+
=
+
−
=
+
−
=
+
1
1
1
1
1
1
1
1
1
1
1
1
)
1
(
1
k
k
k
k
k
k
k
k
v
k
v
v
k
v
k
k
v
k
k
∑
∑
∑
∞
=
∞
=
∞
=
+
−
=
−
−
=
1
1
1
1
1
1
1
1
1
1
k
k
k
k
k
k
v
v
k
v
v
k
v
v
k
)
1
ln(
2
1
1
1
)
1
ln(
v
v
v
N
−
−
=
+
−
−
−
18
,
6
1
9
,
0
1
1
)
9
,
0
1
ln(
)
9
,
0
1
ln(
2
1
1
1
)
1
ln(
)
1
ln(
2
≈
−
−
−
−
=
−
−
−
−
=
v
v
v
N
czyli N musi być równe co najmniej 7
Zadanie 4
t
t
T
q
t
t
P
e
S
V
X
C
V
+
=
+
=
−
−
)
(
)
0
(
2
)
0
(
1
V1: kwota X w momencie T daje
)
(
t
T
r
Xe
−
Jeśli wartość akcji w T
X
X
S
T
−
>
T
S
daje
to
Czyli łącznie
)
(
t
T
r
T
Xe
X
S
−
+
−

X
S
gdy
T
<
to będziemy mieli
)
(
t
T
r
Xe
−
V2: zakładamy, że mamy opcję europejską o
t
P
W związku z reinwestycją otrzymanych dywident liczba akcji na T=1 zatem wartość
wyniesie
T
S
Gdy
T
S
to
X
S
T
>
Gdy
X
S
X
S
T
T
=
+
<
T
S
-
X
to
Gdy
)
(
2
)
(
1
)
(
T
V
S
Xe
X
S
T
V
X
S
T
t
T
r
T
T
=
≥
+
−
=
>
−
Gdy
)
(
2
)
(
1
)
(
T
V
X
Xe
T
V
X
S
t
T
r
T
=
≥
=
<
−
Z tego:
)
(
2
)
(
1
T
V
T
V
≥
(przy założeniu na opcję europejską)
Przy braku arbitrażu możemy przyjąć, że nierówność prawdziwa także w chwili obecnej
Jeżeli zamienimy w V2 opcję europejską na amerykańską wiedząc że:
t
t
t
T
q
t
t
t
T
q
t
t
eur
t
am
t
P
C
X
e
S
P
e
S
X
C
P
P
−
≤
−
→
+
≥
+
≤
−
−
−
−
)
(
)
(
daje
to
analogicznie analizując V3 i V4 dostajemy:
)
(
t
T
r
t
t
t
Xe
S
P
C
−
−
−
≤
−
czyli odpowiedź E jest prawidłowa
Zadanie 5
{
}
R
a
kazdego
dla
mierzalny
)
(
:
gdy
mierzalna
jest
:
∈
>
∈
→
a
x
f
X
x
R
X
f
{
}
A
a
x
f
X
x
OZN
=
>
∈
)
(
:
:
sprawdzamy (a)
( )
( )
=
=
=
=
=
5,6,7,8
i
84
w
1,2,3,4
i
72
1
1
i
i
w
w
w
W
[
)
{
}
1
1
8
7
6
5
1
F
pusty
A
84
a
,
,
,
w
A
72,84
a
F
A
72
a
∈
=
≥
∈
=
∈
∈
Ω
=
<
dla
F
w
w
w
dla
dla
z tego wynika, że (a) TAK
sprawdzamy (b)
[
)
{
}
1
8
7
6
4
1
,
,
,
w
A
72,84
a
F
A
72
a
F
w
w
w
dla
dla
∉
=
∈
∈
Ω
=
<
z tego wynika, że (b) NIE
sprawdzamy c
{
}
8
2
1
3
,...,
,
,
,
w
w
w
pusty
F
Ω
=
sprawdzamy
1
F
- mierzalność
=
8
7
6
5
4
3
2
1
,
w
3
,
,
,
w
6
,
w
9
w
w
w
w
w
W

[
)
{
}
1
6
2
1
1
,...,
,
w
A
3,6
a
F
A
3
a
F
w
w
dla
dla
∉
=
∈
∈
Ω
=
<
z tego wynika, że c NIE
sprawdzamy (d)
[
)
{
}
[
)
{
}
3
3
2
1
3
6
1
3
F
pusty
A
9
,
w
A
9
,
6
,...,
w
A
6
,
3
F
A
3
∈
=
≥
∈
=
∈
∈
=
∈
∈
Ω
=
<
a
F
w
a
F
w
a
a
z tego wynika, że (d) TAK
czyli odpowiedź C jest prawidłowa
Zadanie 6
Bull spread oznacza, że kupujemy 1 opcję kupna z ceną wykonania X1 i wystawiamy 1 opcję
kupna z ceną wykonania X2 oraz X2>X1
Profil wypłaty:
[
)
(
)
1
2
2
1
S
2
S
1
S
2
,
1
S
dla
0
1
S
5
5
5
5
5
5
X
X
X
S
X
X
dla
X
X
X
X
dla
−
=
−
−
−
≥
−
∈
<
Z powyższego i z obrazka widać, że:
Dla
1
5
X
S
=
zaczyna rosnąć więc X1=110 i stąd X2=140
RT
C
p
Xe
S
P
P
−
+
−
=
- PARYTET
( )
35
,
0
07
,
0
5
110
13
,
125
)
1
(
110
125
1
13
,
0
−
⋅
−
−
=
→
+
−
=
e
X
P
e
X
P
C
C
35
,
0
07
,
0
5
140
84
,
126
)
2
(
140
125
)
2
(
84
,
1
−
⋅
−
−
=
→
+
−
=
e
X
P
e
X
P
C
C
43
,
19
71
,
1
30
)
2
(
)
1
(
35
,
0
≈
−
=
−
=
−
e
X
P
X
P
ODP
C
C
Zadanie 7
K(i) – kredyt na koniec i-tego roku
WP(i) – wpłata na koniec i-tego roku
(
)
4
3
2
5
06
,
1
06
,
1
06
,
1
06
,
1
1
06
,
0
4
,
0
06
,
1
)
5
(
+
+
+
+
⋅
⋅
⋅
−
⋅
=
K
K
K
K(10)=K(5)
przez następne 5 lat rata S::
18000
90000
300000
3
,
0
5
=
→
=
⋅
=
S
S
po 5 latach
(
)
1
...
07
,
1
18000
07
,
1
)
10
(
)
15
(
4
5
+
+
−
⋅
=
K
K
08
,
0
;
10
)
15
(
Ra
K
=
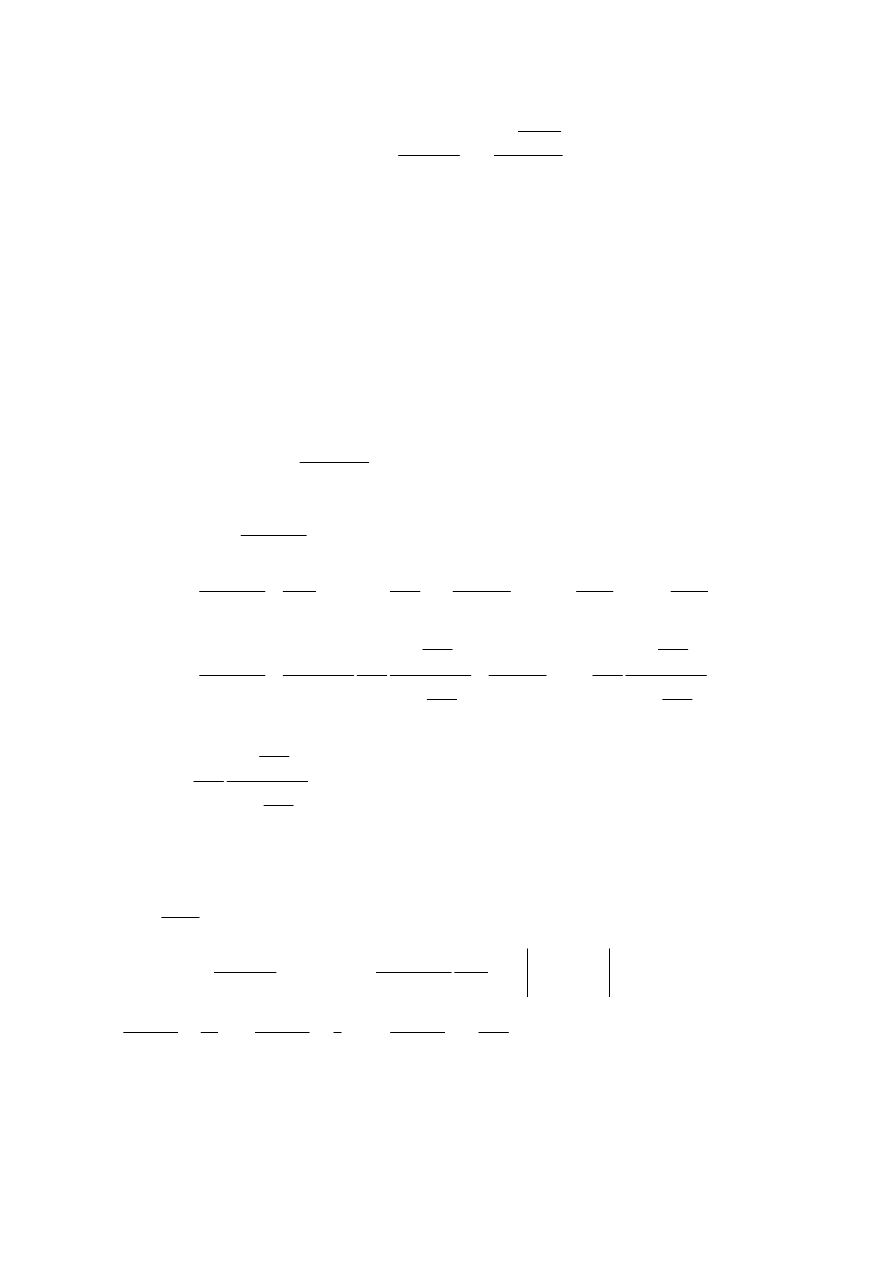
(
)
60005
59409
08
,
0
08
,
1
1
1
07
,
0
1
07
,
1
18000
07
,
1
06
,
0
4
,
0
06
,
1
300000
10
5
5
5
≈
≈
→
−
=
−
−
⋅
⋅
−
R
R
Zadanie 8
KW1 – kwota uzyskana przy stopie 6%
KW2 – kwota uzyskana przy stopie 8%
NAD – nadwyżka
(
)
40
08
,
0
1
08
,
1
08
,
1
2000
02
,
0
)
(
08
,
1
...
08
,
1
2000
)
(
2
02
,
0
2000
02
,
0
)
1
(
2
)
(
08
,
1
2000
08
,
1
)
1
(
2
)
(
2
06
,
1
2000
06
,
1
)
1
(
2
)
(
1
1
+
−
⋅
⋅
=
+
+
=
⋅
+
⋅
−
=
⋅
+
⋅
−
=
⋅
+
⋅
−
=
−
i
i
i
NAD
i
KW
i
KW
i
NAD
i
KW
i
KW
i
KW
i
KW
∑
=
−
=
+
−
⋅
=
5
1
15
15
04
,
1
)
(
06
,
0
1
06
,
1
06
,
1
2000
i
i
i
NAD
ODP
∑
∑
∑
=
=
=
+
⋅
−
+
−
⋅
=
5
1
5
1
15
15
15
15
04
,
1
04
,
1
1
40
04
,
1
1
04
,
1
08
,
0
08
,
1
40
04
,
1
08
,
1
04
,
1
08
,
0
40
06
,
0
1
06
,
1
06
,
1
2000
i
i
i
i
i
+
−
−
⋅
−
−
−
⋅
+
−
⋅
=
04
,
1
1
1
04
,
1
1
1
04
,
1
1
04
,
1
08
,
0
08
,
1
40
04
,
1
08
,
1
1
04
,
1
08
,
1
1
04
,
1
08
,
1
08
,
0
04
,
1
40
06
,
0
1
06
,
1
06
,
1
2000
5
15
5
15
15
)
(
04
,
1
1
1
04
,
1
1
1
04
,
1
1
04
,
1
40
5
15
D
≈
−
−
⋅
+
Zadanie 9
14
,
915
03
,
1
1000
)
0
(
3
=
=
P
(
)
∫
−
=
=
=
+
=
+
=
+
=
03
,
0
03
,
0
2
2
03
,
1
06
,
0
1
03
,
1
1
1000
03
,
1
1
1000
)
1
(
dt
dx
t
x
dx
x
X
E
P
∫
≈
−
=
−
=
=
06
,
1
1
06
,
1
1
2
4
,
943
06
,
1
1
1
6
100000
1
6
100000
1
6
100000
t
dt
t
Zadanie 10
Możliwe scenariusze:

1. A,A,A
2. A,A,B
3. A,B,A
4. A,B,B
p(i) – prawdopodobieństwo scenariusza I
18
,
0
9
,
0
2
,
0
)
4
(
02
,
0
1
,
0
2
,
0
)
3
(
16
,
0
2
,
0
8
,
0
)
2
(
64
,
0
8
,
0
)
1
(
2
=
⋅
=
=
=
⋅
=
=
=
⋅
=
=
=
=
=
BB
AB
BA
AB
AB
AA
AA
AA
p
p
p
p
p
p
p
p
p
p
p
p
(
)
(
)
+
+
+
+
+
+
+
+
=
)
2
(
100
4
4
4
)
1
(
100
4
4
4
2
2
2
3
3
2
p
v
v
v
v
v
v
p
v
v
v
v
ODP
B
A
B
A
A
A
A
A
A
A
(
)
(
)
=
+
+
+
+
+
+
+
+
)
4
(
100
4
4
4
)
3
(
100
4
4
4
2
2
2
2
p
v
v
v
v
v
v
v
p
v
v
v
v
v
v
v
B
A
B
A
B
A
A
B
A
B
A
B
A
A
(
)
(
)
+
⋅
+
⋅
+
⋅
+
⋅
+
⋅
+
⋅
+
⋅
+
⋅
=
16
,
0
9
,
0
95
,
0
100
9
,
0
95
,
0
4
95
,
0
4
95
,
0
4
64
,
0
95
,
0
100
95
,
0
4
95
,
0
4
95
,
0
4
2
2
2
3
3
2
(
)
+
⋅
+
⋅
+
⋅
⋅
+
⋅
+
02
,
0
9
,
0
95
,
0
100
9
,
0
95
,
0
4
9
,
0
95
,
0
4
95
,
0
4
2
2
(
)
05
,
94
18
,
0
9
,
0
95
,
0
100
9
,
0
95
,
0
4
9
,
0
95
,
0
4
95
,
0
4
2
2
≈
⋅
⋅
+
⋅
⋅
+
⋅
⋅
+
⋅
Wyszukiwarka
Podobne podstrony:
1 2009.10.05 matematyka finansowa
2004 10 11 matematyka finansowaid 25165
2009 10 05 praid 26669 Nieznany
1 2006 10 09 matematyka finansowaid 8919
2002 10 12 matematyka finansowaid 21647
2007.10.08 matematyka finansowa
1 2009.04.06 matematyka finansowa
2008.10.06 matematyka finansowa
2009.10.05 prawdopodobie stwo i statystyka
2006 06 05 matematyka finansowaid 25460
2009 11 30 matematyka finansowaid 26676
2009 10 05 prawdopodobie stwo i statystykaid 26670
2009 10 05 mat fizid 26671 Nieznany
2004.10.11 matematyka finansowa
1 2006.10.09 matematyka finansowa
2010.10.04 matematyka finansowa
2009.11.30 matematyka finansowa
2005 12 05 matematyka finansowaid 25347
więcej podobnych podstron