
Egzamin dla Aktuariuszy z 5 czerwca 2006 r.
Matematyka Finansowa
Zadanie 1
)
25
,
0
;
1
,
0
(
~
−
J
r
i
∏
=
+
=
+
10
1
)
1
(
1000
)
1
(
1000
i
i
r
r
∏
∏
∏
+
+
−
+
=
+
=
1
)
1
(
2
)
1
(
)
1
(
2
2
i
i
i
r
r
r
r
r
òòò òò
∏
−
−
−
ú
û
ù
ê
ë
é
+
=
+
=
25
,
0
1
,
0
10
25
,
0
1
,
0
2
10
2
1
10
1
35
,
0
2
)
1
(
...
35
,
0
1
)
1
(
...
r
dr
dr
dr
r
Er
i
10
10
10
25
,
0
1
,
0
2
25
,
0
1
,
0
3
10
25
,
0
1
,
0
10
2
2
35
,
0
35
,
0
2
)
1
(
2
3
)
1
(
1
35
,
0
1
)
1
(
...
2
..
35
,
0
1
)
1
(
...
+
ú
û
ù
ê
ë
é
+
−
ú
û
ù
ê
ë
é
+
=
=
+
+
−
+
=
−
−
−
òò ò
∏
òò ò
∏
r
r
r
dr
r
Er
i
i
i
Z tego wynika:
var
)
(
)
(
)
var(
2
2
=
−
=
x
Er
Er
r
δ
7
,
1
)
(
≈
X
EX
δ
Zadanie 2
Π
Π
>
÷
ø
ö
ç
è
æ
Π
−
Π
⋅
→
>
=
=
6
do
2
od
X
to
0
3
2
3
200
sin
%)
7
(
)
(
0
%)
7
sin(
100000
%)
7
(
nawias
i
f
i
f
f
dla i = 0,04
X=2
Π
04
,
0
=
→
i
÷
ø
ö
ç
è
æ
∪
÷
ø
ö
ç
è
æ
∈
=
=
→
Π
=
=
→
Π
=
=
→
Π
=
200
17
;
07
,
0
200
11
;
04
,
0
200
17
5
07
,
0
4
200
11
3
i
A
i
X
i
X
i
X
(
)
Π
=
Π
=
ú
ú
ú
ú
û
ù
ê
ê
ê
ê
ë
é
Π
Π
+
Π
−
Π
−
Π
=
=
ú
ú
ú
ú
û
ù
ê
ê
ê
ê
ë
é
Π
÷
ø
ö
ç
è
æ
Π
−
Π
−
=
÷
ø
ö
ç
è
æ
Π
−
Π
⋅
=
−
ò
100000
3
200
4
06
,
0
100000
3
200
)
4
cos(
)
5
cos(
)
3
cos(
)
2
cos(
06
,
0
100000
3
200
3
2
3
200
cos
06
,
0
100000
3
2
3
200
sin
06
,
0
100000
0
%);
7
(
)
(
max
A
A
i
di
i
f
i
f
E
28000
08
,
1
95
,
0
100000
≈
⋅
Π
=
ODP
Zadanie 3
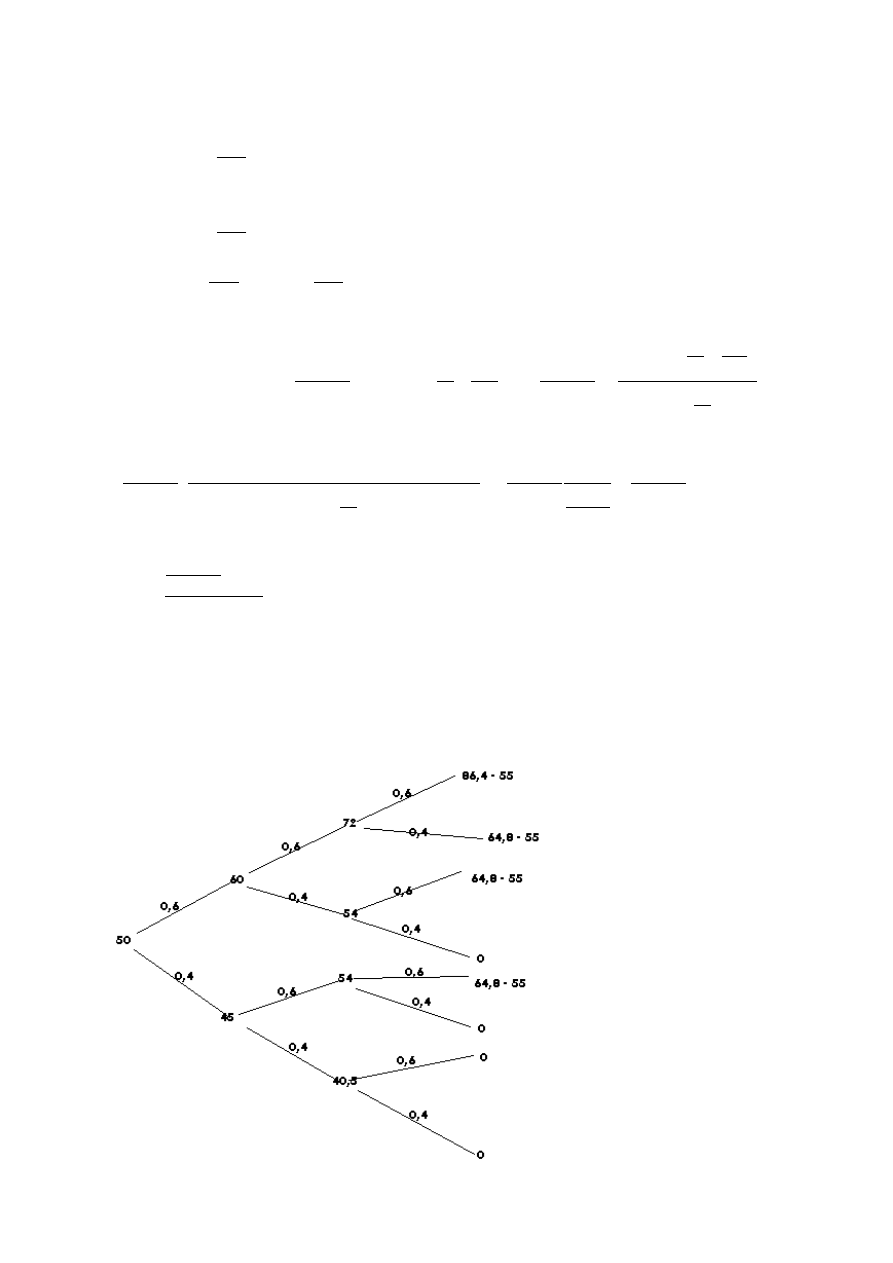
Ró
ż
ne strategie:
î
í
ì
=
î
í
ì
=
î
í
ì
=
wpp
0
40,5
przy
pacimy
gdy
1
wpp
0
54
przy
pacimy
gdy
1
wpp
0
0,6P
pacimy
72
przy
gdy
1
z
y
x
[
] [
]
3
2
2
3
2
2
2
1
,
1
)
55
8
,
64
(
4
,
0
6
,
0
4
,
0
6
,
0
)
55
8
,
64
(
6
,
0
)
55
4
,
86
(
)
4
,
0
6
,
0
4
,
0
2
6
,
0
(
1
,
1
6
,
0
4
,
0
(
−
⋅
+
⋅
⋅
−
+
⋅
−
=
=
⋅
+
⋅
⋅
⋅
+
⋅
+
y
x
z
y
x
P
Trzeba zmaksymalizowa
ć
praw
ą
stron
ę
i lew
ą
zminimalizowa
ć
- znale
źć
maks. P przy
ró
ż
nych strategiach
Z tego wynika,
ż
e z=0 x i y nie
Trzy warianty mo
ż
liwe tzn: x,y=1; x=0,y=1; x=1; y=0
Przy ostatniej strategii wychodzi : P max około 10,65
Zadanie 4
Korzystne dla emitenta gdy:
05
,
0
05
,
1
1000
)
1
(
1000
)
1
(
1000
05
,
1
1000
5
5
5
5
<
⋅
<
+
+
<
r
r
r
0,05
r
gdy
1000
)
1
(
1,06
1000
0,05
r
gdy
)
1
(
05
,
1
1000
)
1
(
06
,
1
1000
10
10
5
5
10
10
>
=
+
<
+
=
+
i
r
i
ï
î
ï
í
ì
>
=
<
−
+
=
0,05
r
0,06
i
0,05
r
1
1
05
,
1
06
,
1
r
i
(
)
%
62
,
5
5
,
0
06
,
0
03
,
0
6
100
)
1
(
3
2
05
,
1
06
,
1
6
100
)
05
,
0
(
06
,
0
)
05
,
0
(
05
,
0
05
,
0
02
,
0
2
3
≈
⋅
+
⋅
−
ú
û
ù
ê
ë
é
+
=
>
+
<
<
=
r
r
P
r
P
r
i
E
Ei
Zadanie 5
2 - 0,03
20 - 0,06
9
8
03
,
0
,
18
03
,
0
06
,
0
20
03
,
0
2
⋅
=
=
→
î
í
ì
=
+
=
+
b
a
b
a
b
a
20
19
19
19
20
19
2
19
100000
18
03
,
0
03
,
0
18
17
75
500
04
,
1
100000
9
8
03
,
0
20
18
03
,
0
...
9
8
03
,
0
3
18
03
,
0
9
8
03
,
0
2
18
03
,
0
75
500
v
Ia
a
B
a
BV
BV
BV
a
KOSZTY
+
úû
ù
êë
é
+
⋅
+
+
=
=
+
÷
ø
ö
ç
è
æ
⋅
+
⋅
+
+
+
÷
ø
ö
ç
è
æ
⋅
+
⋅
+
÷
ø
ö
ç
è
æ
⋅
+
⋅
+
+
=
KOSZTY
WPLYWY
a
B
=
=
20
&
&
3473
18
03
,
0
03
,
0
18
17
100000
75
500
19
19
20
20
19
≈
−
⋅
−
+
+
=
Ia
a
a
v
a
B
&
&
Zadanie 6
647575
1
)
1
(
20
20
...
2
20
1
20
20
20
2
≈
−
+
=
÷÷
ø
ö
çç
è
æ
+
+
÷÷
ø
ö
çç
è
æ
+
÷÷
ø
ö
çç
è
æ
=
v
v
v
v
I
bo:
n
n
a
n
n
a
n
a
n
a
÷÷
ø
ö
çç
è
æ
+
+
÷÷
ø
ö
çç
è
æ
+
÷÷
ø
ö
çç
è
æ
=
+
...
1
0
)
1
(
1
0
Zadanie 7
÷
ø
ö
ç
è
æ
=
÷
ø
ö
ç
è
æ
=
ò
ò
t
t
ds
s
t
a
ds
s
t
a
0
2
2
0
1
1
)
(
exp
)
(
)
(
exp
)
(
δ
δ
5
10
=
=
α
n
t
t
a
t
a
=
)
(
)
(
2
1
rozkład wykładniczy obci
ę
ty
ï
ï
î
ïï
í
ì
=
=
∈
=
⋅
−
−
10
5
1
5
1
)
10
(
)
10
;
0
(
5
1
)
(
e
T
P
T
e
T
f
T

T
a
T
a
T
a
a
ds
s
ds
s
ds
s
ds
s
ds
s
a
T
T
T
T
⋅
=
=
=
÷
ø
ö
ç
è
æ
−
÷
ø
ö
ç
è
æ
=
÷
ø
ö
ç
è
æ
÷
ø
ö
ç
è
æ
=
ò
ò
ò
ò
ò
)
10
(
)
(
)
(
)
10
(
)
(
)
(
exp
)
(
exp
)
(
exp
)
(
exp
)
10
(
2
2
1
2
10
0
0
2
2
0
1
10
2
0
1
δ
δ
δ
δ
δ
(
)
)
10
(
32
,
4
)
10
(
5
5
)
10
(
5
1
10
)
10
(
2
2
2
2
10
0
5
1
2
a
a
e
a
dx
e
x
e
Ea
x
≈
−
=
ú
û
ù
ê
ë
é
+
=
−
−
−
ò
Zadanie 8
UWAGA: przez nast
ę
pnych t lat oznacza,
ż
e pierwsza renta startuje w zerze ale jest
odroczona; duration dotyczy ci
ą
gu wi
ę
c tak jakby płatno
ś
ci za renty (odroczone)
( )
δ
δ
δ
t
t
t
tv
v
a
I
−
−
=
2
2
1
( )
( )
å
å
∞
=
∞
=
=
=
1
1
t
t
t
t
t
t
v
a
I
t
LICZ
v
a
I
CENA
}
}
å
−
−
=
A
t
to
t
t
v
t
tv
tv
LICZ
2
2
latwe
2
2
2
1
1
1
δ
δ
δ
A obliczamy wykorzystuj
ą
c uwag
ę
z tre
ś
ci zadania dla
i
v
+
=
1
1
2
Wtedy:
3
2
2
2
2
2
)
1
(
)
v
(1
A
i
1
v
v
v
v
i
−
+
=
−
=
å
−
−
=
t
t
t
tv
v
v
CENA
2
2
2
2
1
1
1
δ
δ
δ
21
)
1
(
1
1
1
1
1
)
1
(
)
1
(
1
)
1
(
1
)
1
(
1
2
2
2
2
2
2
2
3
2
2
2
2
2
2
2
2
2
≈
−
−
−
−
−
−
+
−
−
−
−
=
v
v
v
v
v
v
v
v
v
v
v
v
v
ODP
δ
δ
δ
δ
δ
δ
Zadanie 9
)
)
1
(
1
(
500
)
1
(
1000
1
1
1
500
10
10
10
−
+
+
=
+
+
÷
ø
ö
ç
è
æ
+
−
=
i
i
i
i
i
P
11
)
1
(
5000
−
+
−
=
i
di
dP
Zadanie 10
1
a
dla
jako ci
ą
g:
t
n
n
t
a
a
a
a
a
a
a
a
a
1
,
0
1
1
,
0
1
,
0
1
10
1
10
3
1
3
2
1
2
15
)
(
15
15
15
...
=
→
=
=
→
=
=
=
=
i mo
ż
na to sprawdzi
ć
:
)
(
a
dla
2
t
1
4
,
1
)
(
4
,
1
15
9
10
...
1
2
2
1
1
10
1
2
+
=
=
→
=
−
=
−
=
t
t
a
a
a
a
a
a
i sprawdzi
ć
15
ln
1
,
0
)
(
)
(
)
(
)
(
exp
)
(
1
1
1
0
1
1
=
′
=
→
÷
ø
ö
ç
è
æ
=
ò
t
a
t
a
t
ds
s
t
a
t
δ
δ
1
4
,
1
4
,
1
)
(
2
+
=
t
t
δ
55
,
1
)
5
(
)
5
(
2
1
≈
δ
δ
Wyszukiwarka
Podobne podstrony:
Egzamin 2006.06.05, rozwiazania zadań aktuarialnych matematyka finansowa
2011 06 20 matematyka finansowaid 27373
2001 06 02 matematyka finansowaid 21606
1 2006 10 09 matematyka finansowaid 8919
2008.06.02 matematyka finansowa
1 2009 10 05 matematyka finansowaid 8924
mat fiz 2006 06 05
2001.06.02 matematyka finansowa
2006.03.20 matematyka finansowa
2006 06 05 prawdopodobie stwo i statystykaid 25461
1 2009.10.05 matematyka finansowa
2002.06.15 matematyka finansowa
2011.06.20 matematyka finansowa
1 2000 06 17 matematyka finansowaid 8918
1 2006.10.09 matematyka finansowa
2006.06.05 prawdopodobie stwo i statystyka
2005 12 05 matematyka finansowaid 25347
2008 06 02 matematyka finansowaid 26453
więcej podobnych podstron