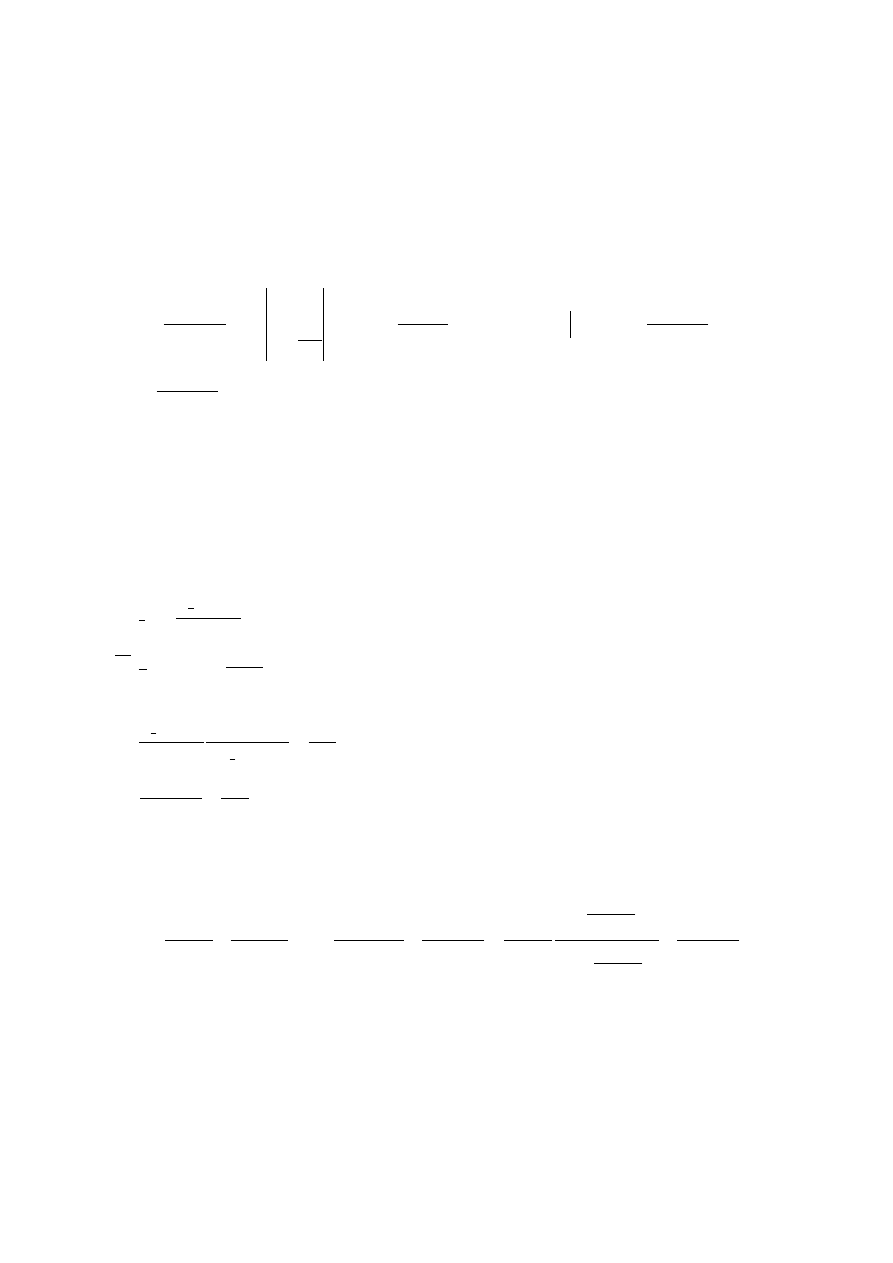
Egzamin dla Aktuariuszy z 2 czerwca 2001 r.
Matematyka Finansowa
Zadanie 1
(
)
[
]
ò
ò
−
−
=
−
−
−
=
−
−
=
=
=
=
−
−
=
=
+
t
t
n
t
n
n
n
y
y
y
n
y
n
n
e
e
e
x
e
x
e
e
dx
x
e
dy
e
e
e
L
e
i
i
0
)
exp(
1
t)
exp(
1
1
ln
ln
1
)
1
(
:
bo
TAK
)
(
δ
δ
δ
δ
δ
δ
δ
δ
δ
δ
δ
δ
δ
δ
δ
1
ln
−
−
=
n
t
n
e
e
e
P
δ
δ
δ
1
i)
(1
i
gdy
tylko
we
nieprawdzi
ogólnie
...
...
...
...
...
...
)
(
)
(
)
(
:
bo
NIE
)
(
2
1000
6
4
2
1000
2
999
5
3
999
998
2
4
3
2
3
2
2
−
+
=
+
+
+
+
=
+
+
+
+
−
−
−
−
−
=
=
−
−
−
+
+
+
+
+
+
+
+
+
+
+
−
+
+
−
=
v
v
v
v
v
v
v
v
v
v
v
v
v
v
v
v
v
v
v
v
v
v
v
v
v
v
L
ii
ò
∞
∞
=
=
−
=
0
2
)
(
)
(
ln
1
)
(
)
(
:
bo
TAK
)
(
v
tv
Ia
i
nv
a
Ia
iii
t
m
n
n
m
n
&
&
)
(
)
(
2
2
)
(
)
(
1
ln
1
)
(
ln
:
m
m
m
n
n
m
n
n
i
vi
P
i
nv
a
i
i
i
nv
a
L
v
wiemy
=
=
=
−
−
=
=
−
δ
δ
&
&
&
&
Zadanie 2
1115
0825
,
1
1050
0825
,
1
03
,
1
1
0825
,
1
03
,
1
1
0825
,
1
75
0825
,
1
1050
0825
,
1
03
,
1
75
...
0825
,
1
03
,
1
75
0825
,
1
75
20
20
20
20
19
2
≈
+
−
÷
ø
ö
ç
è
æ
−
=
+
⋅
+
+
⋅
+
=
ODP

Zadanie 3
%
5
05
,
0
)
1
(
400
86
,
379
144300
)
,
cov(
100
300
2
var
10000
var
90000
)
100
300
var(
400
)
400
(
160000
)
400
var(
=
≈
=
−
≈
=
⋅
⋅
+
+
=
+
=
=
X
OD
X
OD
Y
X
Y
X
Y
X
X
OD
X
Zadanie 4
...
9
7
5
...
9
3
7
2
5
3
2
3
2
+
+
+
+
⋅
+
⋅
+
=
v
v
v
v
v
v
M
L
3
2
2
3
2
4
3
2
)
1
(
5
1
)
1
(
4
4
...
)
1
3
4
(
)
1
2
4
(
5
)
1
(
...
9
3
7
2
5
v
v
v
L
v
v
v
v
a
Ia
v
v
v
v
L
v
v
v
Lv
−
−
=
→
−
+
−
=
+
=
+
+
⋅
+
+
⋅
+
=
−
+
⋅
+
⋅
+
=
∞
∞
2
2
3
2
3
2
)
1
(
3
5
3
2
...
2
2
5
)
1
(
...
7
5
v
v
v
M
v
a
v
v
v
v
M
v
v
Mv
−
−
=
→
+
=
+
+
+
=
−
+
+
=
∞
66
,
39
)
1
)(
3
5
(
5
≈
−
−
−
=
v
v
v
M
L
Zadanie 5
[
]
ú
ú
û
ù
ê
ê
ë
é
−
+
+
−
−
=
ú
û
ù
ê
ë
é
÷
ø
ö
ç
è
æ
+
−
+
+
+
+
−
−
=
−
+
+
−
=
úû
ù
êë
é
+
+
+
+
+
−
=
=
+
+
+
=
−
−
−
3
;
3
;
1
3
2
;
2
1
2
;
1
1
3
3
2
1
)
1
(
1
1
)
1
(
1
1
1
...
)
1
)(
1
1
(
)
1
(
)
1
(
1
)
1
(
1
1
...
)
1
(
1
)
1
(
1
...
)
1
(
j
s
j
n
n
s
z
iK
n
j
n
n
z
iK
III
j
s
j
n
n
z
iK
n
j
n
n
z
iK
II
ziKs
j
ziK
I
j
n
n
j
n
n
j
n
n
n
j
n
n
n
ef
i
K
K
III
II
I
)
1
(
+
=
+
+
+
Z tego wynika:
1
1
)
1
(
)
1
(
)
1
(
1
)
1
(
1
3
3
3
2
2
3
3
2
1
−
ï
ï
þ
ïï
ý
ü
ï
ï
î
ïï
í
ì
+
ú
ú
ú
ú
û
ù
ê
ê
ê
ê
ë
é
+
+
−
+
+
−
+
+
−
+
=
n
A
j
n
n
j
n
j
n
n
j
n
ef
j
s
j
n
s
n
j
j
s
j
n
n
z
i
zis
i
4
4
4
4
4
3
4
4
4
4
4
2
1
gdzie,
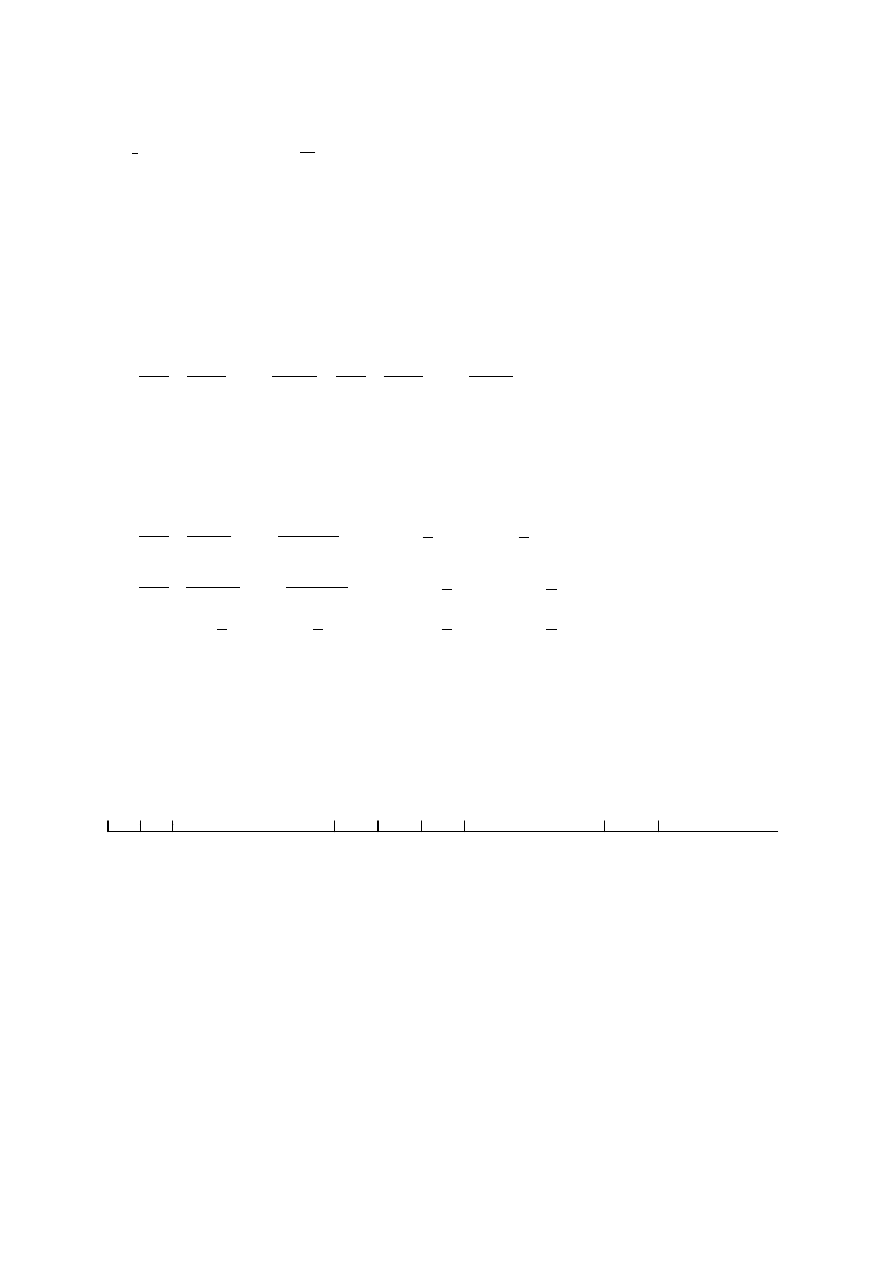
(
)
[
]
)
1
(
)
1
(
)
1
(
)
1
(
)
1
(
)
1
(
)
1
(
)
1
(
)
1
(
1
1
1
+
−
=
+
−
+
+
=
=
+
−
+
−
+
+
+
=
+
−
+
−
+
=
+
n
s
n
j
s
j
n
n
j
n
j
j
n
n
j
A
n
n
n
n
n
n
n
n
St
ą
d wynika
ż
e prawidłowa odpowied
ź
to A.
Zadanie 6
1.
2
1
)
1
(
2
)
1
(
Q
k
P
V
P
Q
k
R
k
k
−
−
=
+
−
=
2.
2
6
5
1
11
10
72
5
2
60
3
4
Q
V
V
Q
R
R
+
+
=
−
+
20
20
2
2
20
20
2
2
03
,
1
...
03
,
1
03
,
1
05
,
1
...
05
,
1
05
,
1
V
V
P
R
R
P
L
+
+
+
=
+
+
+
=
3.
ò
=
+
+
→
−
+
+
=
20
0
2
1
2
1
88
,
7196
20
20
)
06
,
1
ln
exp(
)
20
20
(
85000
Q
Q
P
dt
t
Q
Q
P
Z 1 i 2 wynika po przekształceniach,
ż
e
2
1
Q
Q
=
Z tego i 3 wynika,
ż
e 4.
88
,
7196
40
=
+
Q
P
03
,
0
;
20
03
,
0
;
20
05
,
0
;
20
05
,
0
;
20
03
,
0
;
20
03
,
0
;
20
20
2
05
,
0
;
20
05
,
0
;
20
20
2
)
(
2
)
2
(
)
(
)
(
:
)
(
2
)
2
(
03
,
1
38
...
03
,
1
2
03
,
1
)
(
)
(
05
,
1
19
...
05
,
1
05
,
1
Ia
Q
a
Q
P
Ia
Q
a
Q
P
czyli
Ia
Q
a
Q
P
Q
P
Q
P
P
L
Ia
Q
a
Q
P
Q
P
P
Q
P
L
−
+
=
+
−
−
+
=
−
+
+
−
+
=
+
−
=
+
+
+
+
+
=
To ostanie równanie razem z 4 tworzy układ równa
ń
z niewiadomymi Q i P.
Rozwi
ą
zuj
ą
c je otrzymujemy:
P
Wstawiamy do którego
ś
równania i otrzymujemy około 78000
Zadanie 7
R
R (n-1)k nk (n-1)k k
0 1 2 n-1 n n+1 n+2 2n-1 2n
2k
i
RK - suma kapitału
i
OD - suma odsetek
m
KAP - kapitał spłacony w m-tym roku dla kredytu w wysoko
ś
ci R i płatno
ś
ci K przez n lat
czyli:
)
1
(
−
−
⋅
=
m
n
m
v
K
KAP

Szukamy dla n+k:
n
n
n
n
n
n
n
n
n
KAP
RK
KAP
KAP
RK
KAP
KAP
RK
KAP
KAP
RK
KAP
KAP
RK
KAP
RK
=
+
=
+
+
=
+
+
=
+
=
=
−
−
+
+
2
1
1
2
2
2
1
1
1
2
3
1
2
.....
....
....
....
...
...
n
n
n
n
n
n
n
n
RK
K
OD
RK
K
OD
RK
K
n
OD
RK
nK
OD
RK
K
OD
KAP
K
OD
2
2
1
2
1
2
2
2
1
1
3
3
1
2
2
....
....
)
1
(
....
....
2
−
=
−
=
−
−
=
−
=
−
=
−
=
−
−
+
+
+
+
[
]
k
n
k
n
n
k
k
n
RK
K
k
n
OD
KAP
KAP
RK
+
+
+
−
−
−
=
+
+
=
)
1
(
....
Z tego mamy:
)
1
(
)
1
(
)
1
)(
1
(
1
1
+
−
+
−
+
+
−
−
−
−
+
−
=
k
n
k
n
k
n
k
n
v
v
v
v
v
k
n
RK
OD
Zadanie 8
Przy ustalonej liczbie kredytów podział optymalny oznacza,
ż
e dzielimy całkowity kredyt na
równe cz
ęś
ci - wtedy minimalny koszt.
Sprawdzamy dla n=1,2,....10
Koszt wynosi:
14 000 dla n=2
12200 dla n=3
13800 dla n=4
14000 dla n=5
14400 dla n=6
15300 dla n=7
15600 dla n=9
Odpowied
ź
: n=3

Zadanie 9
Na podstawie teorii:
(
)
(
)
(
)
%
8
%,
7
1
1
1
1
)
1
(
1
)
1
(
2
)
1
(
1
1
1
1
1
)
1
(
1
1
1
)
1
(
=
=
→
−
ú
ú
û
ù
ê
ê
ë
é
+
+
=
→
+
=
+
+
+
+
+
+
i
i
i
i
i
i
i
i
t
t
t
t
t
t
t
t
Zadanie 10
)
1
(
100000
)
(
)
1
(
100000
)
1
2
exp(
100000
)
(
)
1
(
100000
)
1
1
exp(
100000
)
(
0
2
2
0
t
t
t
C
t
ds
s
s
t
B
t
ds
s
t
A
t
t
−
=
+
=
+
=
+
=
+
=
ò
ò
Czyli maksimum osi
ą
gane dla t=0,5 bo to parabola z wierzchołkiem w t=0,5.
Wyszukiwarka
Podobne podstrony:
2001.06.02 matematyka finansowa
2008.06.02 matematyka finansowa
2008 06 02 matematyka finansowaid 26453
Egzamin 2001.06.02, rozwiazania zadań aktuarialnych matematyka finansowa
2011 06 20 matematyka finansowaid 27373
2001 03 24 matematyka finansowaid 21604
2001.03.24 matematyka finansowa
2001.06.02 prawdopodobie stwo i statystyka
2001 06 02 prawdopodobie stwo i statystykaid 21607
mat fiz 2001 06 02
2006 06 05 matematyka finansowaid 25460
2002.06.15 matematyka finansowa
2011.06.20 matematyka finansowa
1 2000 06 17 matematyka finansowaid 8918
2001 06 02 pra
2002 06 15 matematyka finansowaid 21641
2011 06 20 matematyka finansowaid 27373
więcej podobnych podstron