Egzamin dla Aktuariuszy z 2 czerwca 2008 r.
Matematyka Finansowa
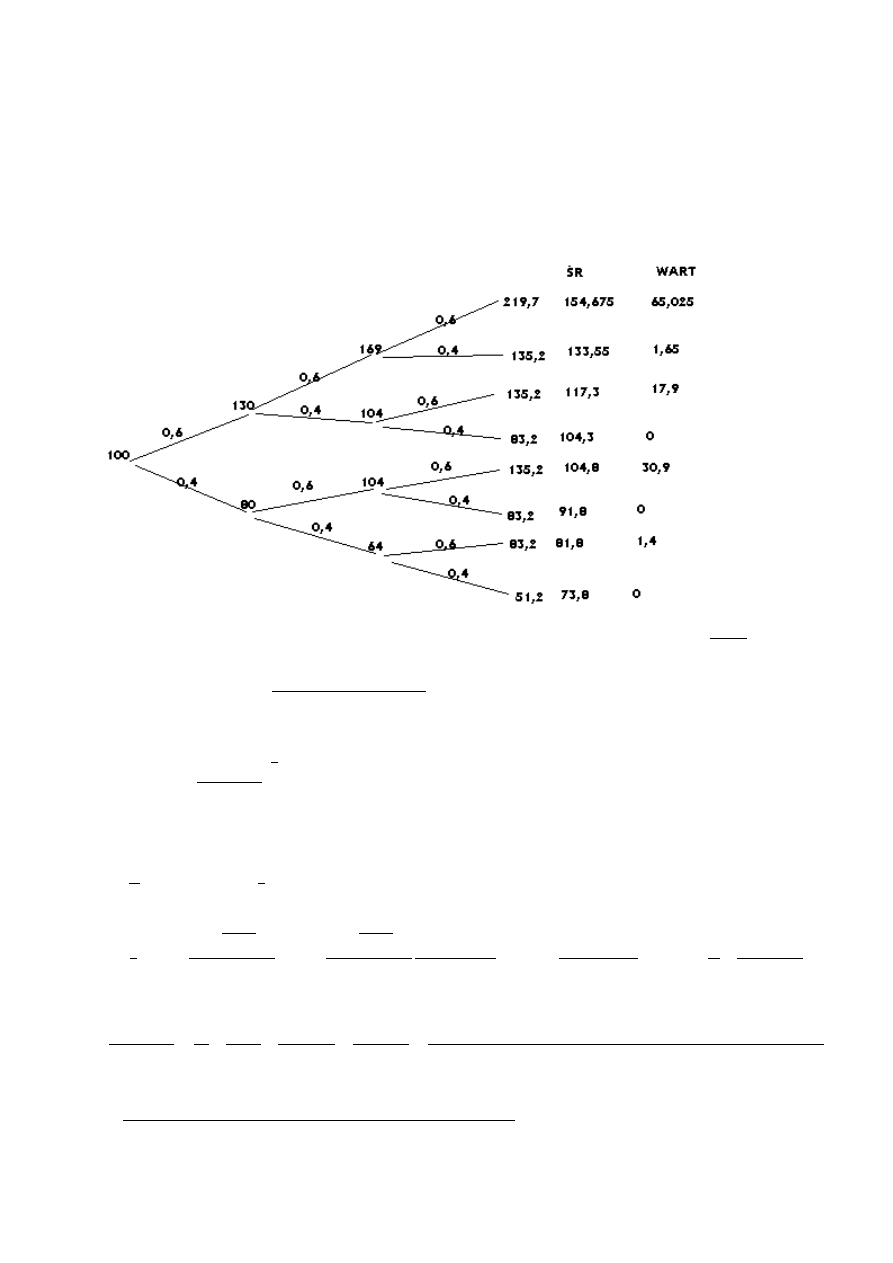
Zadanie 1
WART=max(X-ŚR;0)
(
)
3
2
2
2
2
3
15
,
1
1
4
,
1
4
,
0
6
,
0
9
,
30
4
,
0
6
,
0
9
,
17
4
,
0
6
,
0
65
,
1
4
,
0
6
,
0
025
,
65
6
,
0
⋅
⋅
+
⋅
+
⋅
+
⋅
+
⋅
=
CENA
5
,
17
0
;
4
150
160
120
100
150
max
=
÷
ø
ö
ç
è
æ
+
+
+
−
=
ZWROT
ZWROT
i
CENA
=
+
3
)
1
(
%
6
,
7
%
46
,
7
1
3
1
≈
≈
−
÷
ø
ö
ç
è
æ
=
=
CENA
ZWROT
i
ODP
Zadanie 2
)
07
,
0
;
03
,
0
(
10000
;
3
004
,
0
;
36
J
I
Ea
Xs
I
≅
=
ò
ò
ò
÷÷
ø
ö
çç
è
æ
+
−
=
+
−
+
=
−
÷
ø
ö
ç
è
æ
+
−
=
÷
÷
÷
÷
÷
ø
ö
ç
ç
ç
ç
ç
è
æ
÷
ø
ö
ç
è
æ
+
−
=
07
,
0
03
,
0
07
,
0
03
,
0
07
,
0
03
,
0
3
3
3
3
3
;
3
)
1
(
1
1
25
)
1
(
1
)
1
(
25
03
,
0
07
,
0
1
1
1
1
1
1
1
x
x
x
x
x
x
x
x
I
I
E
Ea
I
(
) (
) (
)
=
+
+
+
+
+
+
+
+
+
+
=
+
+
+
+
+
+
=
+
x
x
Dx
x
x
C
x
x
x
B
x
x
x
A
x
D
x
C
x
B
x
A
x
x
3
2
3
2
3
2
3
2
3
)
1
(
2
3
3
1
)
1
(
)
1
(
1
)
1
(
1
x
x
A
D
C
B
A
x
C
B
A
x
B
A
x
3
2
3
)
1
(
)
3
(
)
2
3
(
)
(
+
+
+
+
+
+
+
+
+
+
=

3
2
3
)
1
(
1
)
1
(
1
1
1
1
)
1
(
1
1
0
1
1
3
1
0
2
3
1
1
1
0
3
0
2
3
0
x
x
x
x
x
x
D
D
C
C
B
A
A
D
C
B
A
C
B
A
B
A
+
−
+
−
+
−
=
+
→
ï
ï
ï
ï
î
ïï
ï
ï
í
ì
−
=
=
+
−
−
−
=
=
+
−
−
=
=
→
ï
ï
î
ï
ï
í
ì
=
=
+
+
+
=
+
+
=
+
ò
ò
=
÷
ø
ö
ç
è
æ
+
+
=
=
+
=
÷÷
ø
ö
çç
è
æ
+
+
+
+
+
=
07
,
0
03
,
0
07
,
1
03
,
1
3
2
3
2
3
1
1
1
25
1
)
1
(
1
)
1
(
1
1
1
25
t
t
t
t
x
x
x
x
Ea
I
ú
û
ù
ê
ë
é
⋅
+
+
−
⋅
−
−
=
úû
ù
êë
é
−
−
=
2
2
07
,
1
03
,
1
2
03
,
1
2
1
03
,
1
1
03
,
1
ln
07
,
1
2
1
07
,
1
1
07
,
1
ln
25
2
1
1
ln
25
t
t
t
705
1
004
,
1
10000
004
,
0
36
3
≈
−
⋅
⋅
=
I
Ea
X
Zadanie 3
53
0
=
S
K=50; T=0,75; r=10%;
S
P
K
R
S
C
K
R
σ
P
C
−
−
=
−
+
=
=
;
%;
20
Chcemy by:
S
P
-K
S
-
C
K
czyli
+
+
=
+
−
=
P
C
R
R
100=P+2S-C
2
100
P
C
S
−
+
=
C,P wyznaczone dla
53
0
=
S
WIEMY:
rT
Ke
S
P
C
−
−
=
−
0
Z tego:
3
,
53
2
50
53
100
075
,
0
≈
−
+
=
−
e
S
czyli zmiana wzrost o 0,3
Zadanie 4
(i)TAK
(
) (
)
0
...
1
1
1
+
=
Φ
+
+
+
=
Φ
+
+
n
n
n
n
n
n
S
X
X
X
E
S
E
(ii)TAK
(
)
(
)
(
)
=
Φ
−
−
+
+
+
=
Φ
−
−
+
+
n
n
n
n
n
n
X
X
X
E
n
S
E
1
...
1
2
1
1
2
1
(
)
(
)
(
)
=
Φ
−
−
+
+
+
+
+
+
=
+
+
n
n
n
n
n
n
X
X
X
X
X
X
E
1
...
2
...
2
1
1
1
2
1
n
S
n
S
S
n
n
n
−
=
−
−
+
⋅
+
=
2
2
1
1
0
2
(iii)TAK
(
)
(
) (
)
n
n
n
X
E
X
E
E
Φ
=
Φ
Φ
+
1
1
1

Zadanie 5
+
⋅
⋅
⋅
⋅
+
⋅
⋅
⋅
+
⋅
⋅
+
⋅
+
=
04
,
1
07
,
1
06
,
1
08
,
1
1
,
1
07
,
1
06
,
1
08
,
1
1
,
1
06
,
1
08
,
1
1
,
1
08
,
1
1
,
1
1
,
1
300000
X
X
X
X
X
+
+
+
+
+
+
⋅
+
+
⋅
⋅
⋅
⋅
⋅
+
3
2
...
1
,
1
1
...
08
,
1
1
,
1
1
1
,
1
1
05
,
1
04
,
1
07
,
1
06
,
1
08
,
1
1
,
1
XA
XA
XAA
XA
XA
X
A
4
4
4
4
4
3
4
4
4
4
4
2
1
=
+
+
+
+
+
+
5
4
4
3
...
1
,
1
1
...
1
,
1
1
XA
XA
XA
XA
ú
ú
ú
û
ù
ê
ê
ê
ë
é
+
+
+
+
+
⋅
⋅
⋅
⋅
+
+
⋅
⋅
+
⋅
+
=
B
A
B
A
B
A
AB
A
X
B
4
3
2
04
,
1
07
,
1
06
,
1
08
,
1
1
,
1
1
...
06
,
1
08
,
1
1
,
1
1
08
,
1
1
,
1
1
1
,
1
1
4
4
4
4
4
4
4
4
4
4
4
4
3
4
4
4
4
4
4
4
4
4
4
4
4
2
1
[
]
A
A
XB
B
A
B
A
B
A
AB
B
X
−
−
=
+
+
+
+
=
1
1
5
4
3
2
(
)
24018
1
)
1
(
300000
5
≈
−
−
=
A
B
A
X
Zadanie 6
W (A) (B) i (E) rozpatrujemy 1 zł
W C i D rozpatrujemy 1USD
(A) kredyt w PLN, dep w EUR
27
,
3
04
,
1
7
,
0
2
,
2
1
⋅
⋅
=
DEP
KREDYT=1,09
(DEP – zwrot z depozytu 1 zł w zł; KREDYT>DEP czyli NIE)
analogicznie dalej sprawdzamy
(B) kredyt USD, dep PLN DEP=1,06 KREDYT=1/2,2*1,04*2,35 NIE
kredyt PLN, dep USD
DEP=1/2,2*1,02*2,35 KREDYT=1,09
(C) kredyt USD, dep EUR
DEP=0,7*1,04*1/0,72
KREDYT=1,04 NIE
kredyt EUR, dep USD
DEP=1,02
KREDYT=0,7*1,06*1/0,72 NIE
(D) kredyt EUR, dep USD
DEP=1,02
KREDYT=0,7*1,06*1,039 NIE
kredyt USD, dep EUR
DEP=0,7*1,04*1,39 KREDYT=1,04 NIE
(E) kredyt EUR, dep PLN
DEP=1,06
KREDYT=1/2,2*0,7*1,06*1/0,32=1,05 TAK
czyli odpowied
ź
(E) jest prawidłowa
Zadanie 7
Z – zgromadzone
ś
rodki
+
+
+
⋅
⋅
=
120
119
120
120
0025
,
1
003
,
1
)
30
3500
(
100
0025
,
1
003
,
1
3500
100
K
K
Z
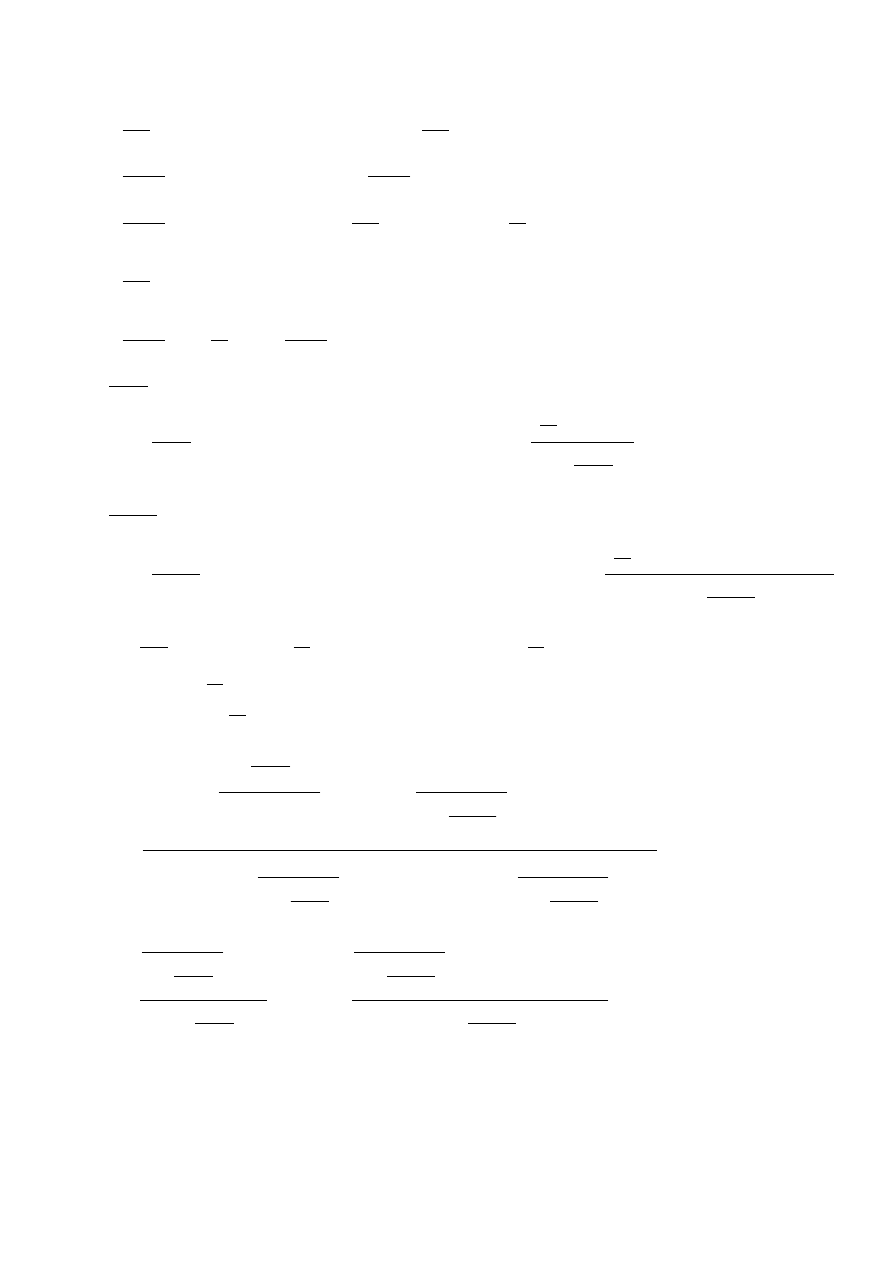
+
⋅
⋅
+
+
+
⋅
+
+
120
120
118
0025
,
1
003
,
1
)
30
119
3500
(
100
...
0025
,
1
003
,
1
)
30
2
3500
(
100
K
K
+
+
⋅
+
+
+
⋅
+
+
+
...
0025
,
1
)
30
121
3500
(
100
3
0025
,
1
)
30
120
3500
(
100
3
119
120
K
K
+
⋅
⋅
=
⋅
+
+
+
003
,
0
;
120
120
0025
,
1
3500
100
0025
,
1
)
30
239
3500
(
100
3
s
K
K
&
&
(
)
+
⋅
+
+
⋅
+
⋅
+
4
4
4
4
4
4
4
8
4
4
4
4
4
4
4
7
6
A
K
003
,
1
119
...
003
,
1
2
003
,
1
0025
,
1
30
100
118
119
120
(
)
4
4
4
4
4
4
4
4
4
8
4
4
4
4
4
4
4
4
4
7
6
&
&
B
K
s
K
0025
,
1
239
...
0025
,
1
121
0025
,
1
120
30
100
3
3500
100
3
119
120
0025
,
0
;
120
⋅
+
+
⋅
+
⋅
+
+
+
+
119
...
003
,
1
2
003
,
1
003
,
1
117
118
+
+
⋅
+
=
A
003
,
1
1
1
119
119
003
,
1
...
003
,
1
003
,
1
003
,
1
1
1
003
,
0
;
119
118
119
−
−
=
→
−
+
+
+
=
÷
ø
ö
ç
è
æ
−
s
A
A
&
&
239
...
0025
,
1
121
0025
,
1
120
0025
,
1
118
119
+
+
⋅
+
⋅
=
B
0025
,
1
1
1
239
0025
,
1
120
239
0025
,
1
...
0025
,
1
0025
,
1
120
0025
,
1
1
1
120
0025
,
0
;
119
119
120
−
−
⋅
+
=
→
−
+
+
+
⋅
=
÷
ø
ö
ç
è
æ
−
s
B
B
&
&
[
]
+
+
+
⋅
+
⋅
=
B
s
A
s
K
Z
30
3500
0025
,
1
30
0025
,
1
3500
100
0025
,
0
;
120
120
003
,
0
;
120
120
&
&
&
&
B
s
30
03
,
0
3500
03
,
0
0025
,
0
;
120
⋅
+
⋅
+
&
&
Z
a
RENTA
=
=
002
,
0
;
120
2000
gdzie
B
A
B
K
,
30
0025
,
1
1
1
1
0025
,
1
3500
0025
,
1
30
003
,
1
1
1
1
003
,
1
0025
,
1
3500
100
30
03
,
0
0025
,
1
1
1
1
0025
,
1
3500
03
,
0
02
,
0
002
,
1
1
1
2000
120
120
120
120
120
120
+
−
−
+
⋅
+
−
−
⋅
ú
ú
ú
ú
ú
û
ù
ê
ê
ê
ê
ê
ë
é
⋅
−
−
−
⋅
−
÷
ø
ö
ç
è
æ
−
=
003
,
1
1
1
119
003
,
1
1
1
1
003
,
1
119
−
−
−
−
=
A
0025
,
1
1
1
239
0025
,
1
120
0025
,
1
1
1
1
0025
,
1
120
119
−
−
⋅
+
−
−
=
B
i wychodzi około 7,86
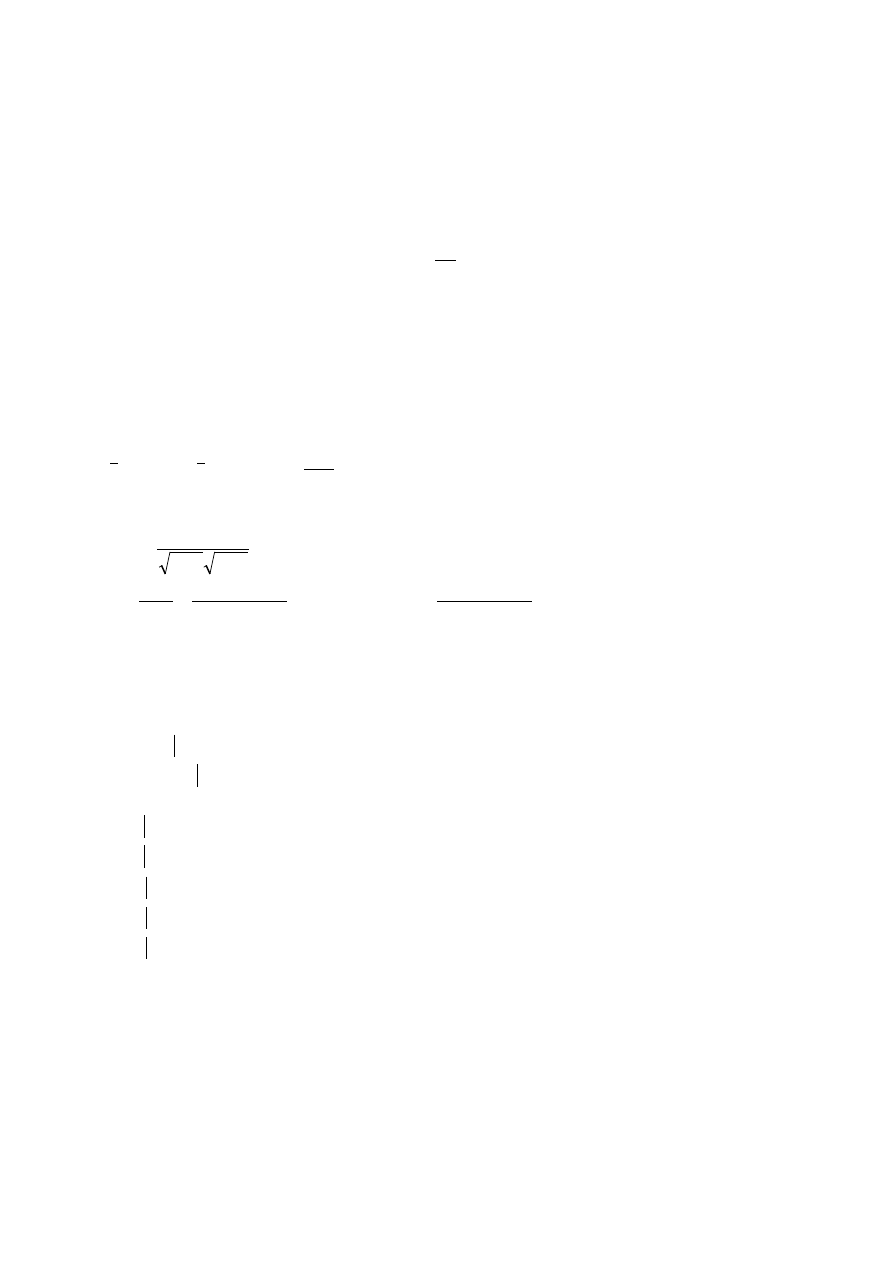
Zadanie 8
P(0,3) – to jest cena jednostkowa czyli jest to dyskonto
Aby policzy
ć
w milionach:
ò
=
−
=
−
=
−
−
−
120
100
2
,
0
12
,
0
08
,
0
)
400
4
(
40
1
)
0
;
400
4
max(
x
x
x
e
x
e
e
X
E
ODP
[
]
[
]
=
−
−
−
−
=
−
−
−
120
100
2
,
0
120
100
2
,
0
2
,
0
5
10
25
5
1
,
0
x
x
x
e
e
xe
(
) (
)
=
−
−
+
+
−
−
=
−
−
−
−
−
−
24
20
20
20
24
24
5
5
10
25
500
25
600
1
,
0
e
e
e
e
e
e
(
)
4
20
20
24
5
1
5
,
2
5
,
2
5
,
12
−
−
−
−
−
=
+
−
=
e
e
e
e
Zadanie 9
(
)
2
M
iM
i
f
M
i
f
i
σ
σ
β
r
r
β
r
r
=
−
=
−
)
1
,
0
22
,
0
(
1
,
0
−
+
=
β
r
X
(
)
5
,
0
6
,
0
14
,
0
cov
25
,
0
36
,
0
,
cov
14
,
0
⋅
⋅
=
→
=
M
X
r
r
%
4
,
11
36
,
0
5
,
0
6
,
0
14
,
0
12
,
0
1
,
0
36
,
0
5
,
0
6
,
0
14
,
0
36
,
0
cov
=
⋅
⋅
+
=
→
⋅
⋅
=
=
ODP
β
Zadanie 10
A= 0,25*110+0,75*80=87,5 NIE
B = 0,25*160+0,75*110=122,5 nie równa si
ę
130 czyli NIE
C
(
)
110
5
,
107
100
75
,
0
130
25
,
0
0
1
≠
=
⋅
+
⋅
=
F
S
E
NIE
D
(
)
110
107,5
bo
0
0
1
<
<
S
F
S
E
NIE
SPRAWDZAMY E
(
)
110
107,5
bo
0
0
1
≤
≤
S
F
S
E
(
)
1
1
1
1
S
S
F
S
E
≤
=
OK.
(
)
110
625
,
75
75
,
0
80
25
,
0
75
,
0
110
25
,
0
160
2
2
0
2
≤
=
⋅
+
⋅
⋅
+
⋅
=
F
S
E
OK.
(
)
130
5
,
122
110
75
,
0
160
25
,
0
130
1
2
≤
=
⋅
+
⋅
=
=
F
S
E
OK.
(
)
100
5
,
87
80
75
,
0
110
25
,
0
100
1
2
≤
=
⋅
+
⋅
=
=
F
S
E
OK.
czyli (E) odpowied
ź
prawidłowa
Wyszukiwarka
Podobne podstrony:
2008.06.02 matematyka finansowa
2001 06 02 matematyka finansowaid 21606
2001.06.02 matematyka finansowa
2001 06 02 matematyka finansowaid 21606
2011 06 20 matematyka finansowaid 27373
mat fiz 2008 06 02
2008.06.02 prawdopodobie stwo i statystyka
2008 03 17 matematyka finansowaid 26447
2008 06 02 prawdopodobie stwo i statystykaid 26454
2006 06 05 matematyka finansowaid 25460
2002.06.15 matematyka finansowa
2011.06.20 matematyka finansowa
2008.12.15 matematyka finansowa
2008.03.17 matematyka finansowa
1 2000 06 17 matematyka finansowaid 8918
2008 12 15 matematyka finansowaid 26464
2002 06 15 matematyka finansowaid 21641
2011 06 20 matematyka finansowaid 27373
więcej podobnych podstron