
Egzamin dla Aktuariuszy z 15 grudnia 2008 r.
Matematyka Finansowa
Zadanie 1
−
⋅
=
⋅
+
⋅
∆
−
⋅
=
⋅
+
⋅
∆
)
0
;
200
200
85
,
0
max(
06
,
1
85
,
0
200
)
0
;
200
200
1
,
1
max(
06
,
1
1
,
1
200
0
0
0
0
B
B
5
2
20
50
0
06
,
1
170
20
06
,
1
220
0
0
0
0
0
0
=
∆
→
=
∆
→
=
+
∆
=
+
∆
B
B
czyli:
15
,
64
06
,
1
68
88
20
06
,
1
20
06
,
1
5
2
220
0
0
0
−
≈
−
=
−
=
=
+
⋅
B
B
B
Zadanie 2
Dla długiej pozycji:
Opcja kupna -
(
)
0
;
max
X
S
T
−
Opcja sprzedaży -
(
)
0
;
max
T
S
X
−
Dla krótkiej pozycji:
Opcja kupna:
(
)
0
;
max
X
S
T
−
−
Opcja sprzedaży:
(
)
0
;
max
T
S
X
−
−
SPRAWDZAMY:
a)
( ) (
)
.....
4
2
06
,
0
3
2
1
+
+
+
−
=
T
T
e
p
p
c
S
F
NIE
b)
( ) (
)
....
4
2
06
,
0
3
2
1
+
−
+
−
=
T
T
e
c
c
p
S
F
NIE
c)
( ) (
)
(
)
(
)
(
)
0
;
max
4
0
;
max
2
0
;
max
4
2
3
2
1
06
,
0
3
2
1
X
S
X
S
S
X
e
c
c
p
S
F
T
T
T
T
T
−
−
−
+
−
−
+
−
=
1.
1
X
S
T
<
(
)
(
)
T
T
S
X
e
c
c
p
−
−
+
−
1
06
,
0
3
2
1
4
2
OK.
2.
2
1
X
S
X
T
<
≤
(
)
T
e
c
c
p
06
,
0
3
2
1
4
2
+
−
OK.
3.
3
2
X
S
X
T
<
≤
(
)
(
)
2
06
,
0
3
2
1
2
4
2
X
S
e
c
c
p
T
T
−
+
+
−
OK.

4.
3
X
S
T
≥
(
)
(
) (
)
(
)
T
T
T
T
T
e
c
c
p
X
X
S
X
S
X
S
e
c
c
p
06
,
0
3
2
1
3
2
3
2
06
,
0
3
2
1
4
2
4
2
2
4
2
4
2
+
−
+
+
−
−
=
−
−
−
+
+
−
OK.
czyli odpowiedź C jest prawidłowa
Zadanie 3
Ponieważ obie obligacje są takie same to w przypadku obligacji (B) mamy dodatkową
możliwość konwersji więc cena tej obligacji nie może być mniejsza od ceny obligacji A
Dlatego
)
0
(
)
0
(
B
A
P
P
≤
Zadanie 4
a – ilość obligacji P(0,1)
b – ilość obligacji P(0,2)
c – ilość obligacji P(0,3)
d – ilość obligacji P(0,4)
a,b,c,d – całkowite, mogą być ujemne
1. 0,9a+0,81b+0,729c+0,684d=0 - bo wydajemy 0
ż
eby nie było arbitrażu to w każdym wariancie zarobimy 0 tzn.
=
+
+
+
=
+
+
+
=
+
+
+
0
86
,
0
92
,
0
0
75
,
0
805
,
0
9
,
0
0
7
,
0
77
,
0
88
,
0
xd
c
b
a
d
c
b
a
d
c
b
a
1. mnożymy przez
0
76
,
0
81
,
0
9
,
0
9
10
=
+
+
+
→
d
c
b
a
2.
Układ równań rozpisujemy uwzględniając 2.
2
;
9
2
16
0
)
76
,
0
(
100
5
2
5
10
4
2
6
0
)
76
,
0
(
05
,
0
02
,
0
0
01
,
0
005
,
0
0
06
,
0
04
,
0
02
,
0
−
=
−
−
=
→
=
−
+
+
−
=
−
−
=
→
=
−
+
+
=
−
−
=
−
−
−
d
c
c
b
d
x
d
c
b
c
d
c
b
d
d
x
c
b
d
c
d
c
b
Z tego:
84
,
0
76
,
0
)
2
(
04
,
0
16
,
0
76
,
0
100
4
16
76
,
0
100
5
2
=
+
−
⋅
+
=
+
+
=
→
+
−
−
=
d
c
d
x
d
c
b
x
Zadanie 5
4
4
4
4
8
4
4
4
4
7
6
4
4
4
4
4
8
4
4
4
4
4
7
6
B
A
v
v
v
v
v
v
v
X
ODP
....
7
2
5
2
3
2
....
7
2
5
2
3
2
2
6
4
2
7
5
3
+
+
+
+
+
+
+
+
=
=
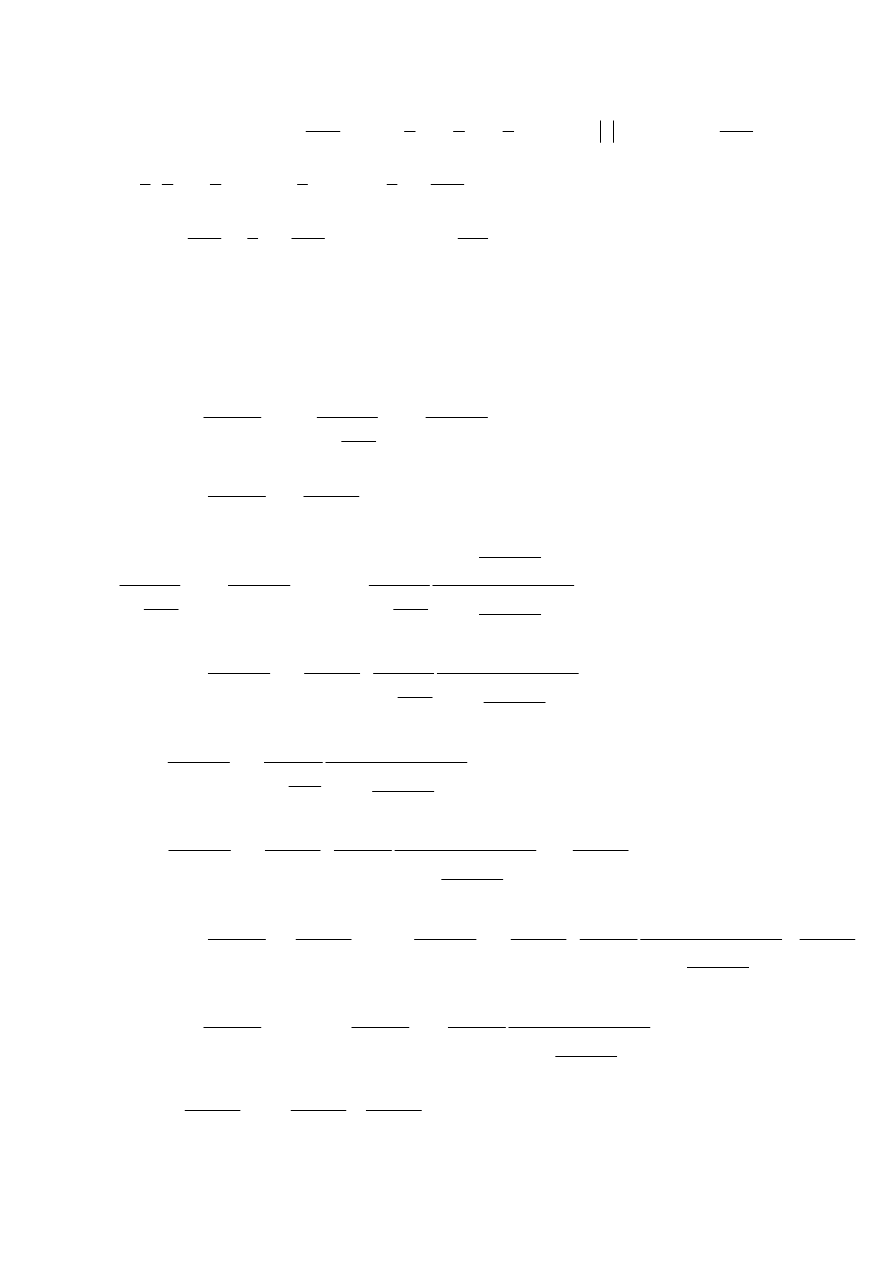
z Taylora wiadomo, że
−
+
=
→
<
+
+
+
+
=
−
+
v
v
A
x
dla
x
x
x
x
x
x
1
1
ln
1
.....
7
2
5
2
3
2
2
1
1
ln
7
5
3
(
)
−
−
+
=
−
=
+
+
=
v
v
v
v
v
A
v
v
v
v
B
2
1
1
ln
1
2
1
...
5
2
3
2
1
5
3
6
02
,
6
04
,
1
1
gdzie
2
1
1
ln
1
1
1
ln
≈
≈
→
=
−
−
+
+
−
+
=
ODP
v
v
v
v
v
v
v
ODP
Zadanie 6
∫
∫
∫
+
=
t
t
s
w
t
s
ds
dw
s
a
ds
t
A
0
0
exp
)
(
exp
)
(
δ
δ
∫
∫
∫
+
+
+
+
=
t
t
s
t
ds
dw
w
A
s
A
ds
s
A
t
A
0
0
)
(
1
1
exp
)
(
1
1
2
)
(
1
1
exp
)
(
)
(
)
(
1
1
)
(
1
1
exp
)
(
0
t
B
t
A
ds
s
A
t
A
t
′
+
+
⋅
+
=
′
∫
∫
∫
∫
∫
∫
=
+
+
+
=
+
+
t
t
s
t
t
s
t
B
ds
dw
w
A
dw
w
A
s
A
ds
dw
w
A
s
A
0
0
0
0
)
(
)
(
1
1
exp
)
(
1
1
exp
)
(
1
1
2
)
(
1
1
exp
)
(
1
1
2
∫
∫
∫
+
+
+
+
+
=
′
t
s
t
dw
w
A
s
A
t
A
dw
w
A
t
B
0
0
0
)
(
1
1
exp
1
)
(
1
1
2
)
(
1
1
)
(
1
1
exp
)
(
=
+
+
+
+
∫
∫
t
t
dw
w
A
t
A
dw
w
A
0
0
)
(
1
1
exp
1
)
(
1
1
2
)
(
1
1
exp
∫
∫
∫
+
+
+
+
+
+
=
t
s
t
t
A
t
A
ds
dw
w
A
s
A
s
A
t
A
dw
w
A
0
0
0
)
(
1
)
(
2
)
(
1
1
exp
1
)
(
1
)
(
2
)
(
1
1
)
(
1
1
exp
∫
∫
∫
∫
+
+
+
+
+
+
+
+
+
=
′
t
s
t
t
t
A
t
A
dw
w
A
s
A
s
A
t
A
dw
w
A
t
A
ds
s
A
t
A
0
0
0
0
)
(
1
)
(
2
)
(
1
1
exp
1
)
(
1
)
(
2
)
(
1
1
)
(
1
1
exp
)
(
1
1
)
(
1
1
exp
)
(
∫
∫
∫
∫
→
+
+
+
+
+
=
t
s
t
t
ds
dw
w
A
s
A
s
A
ds
s
A
ds
s
A
t
A
0
0
0
0
)
(
1
1
exp
1
)
(
1
)
(
2
)
(
1
1
exp
)
(
1
1
exp
)
(
)
(
1
)
(
3
)
(
1
)
(
2
)
(
)
(
1
1
)
(
t
A
t
A
t
A
t
A
t
A
t
A
t
A
+
=
+
+
+
=
′
→
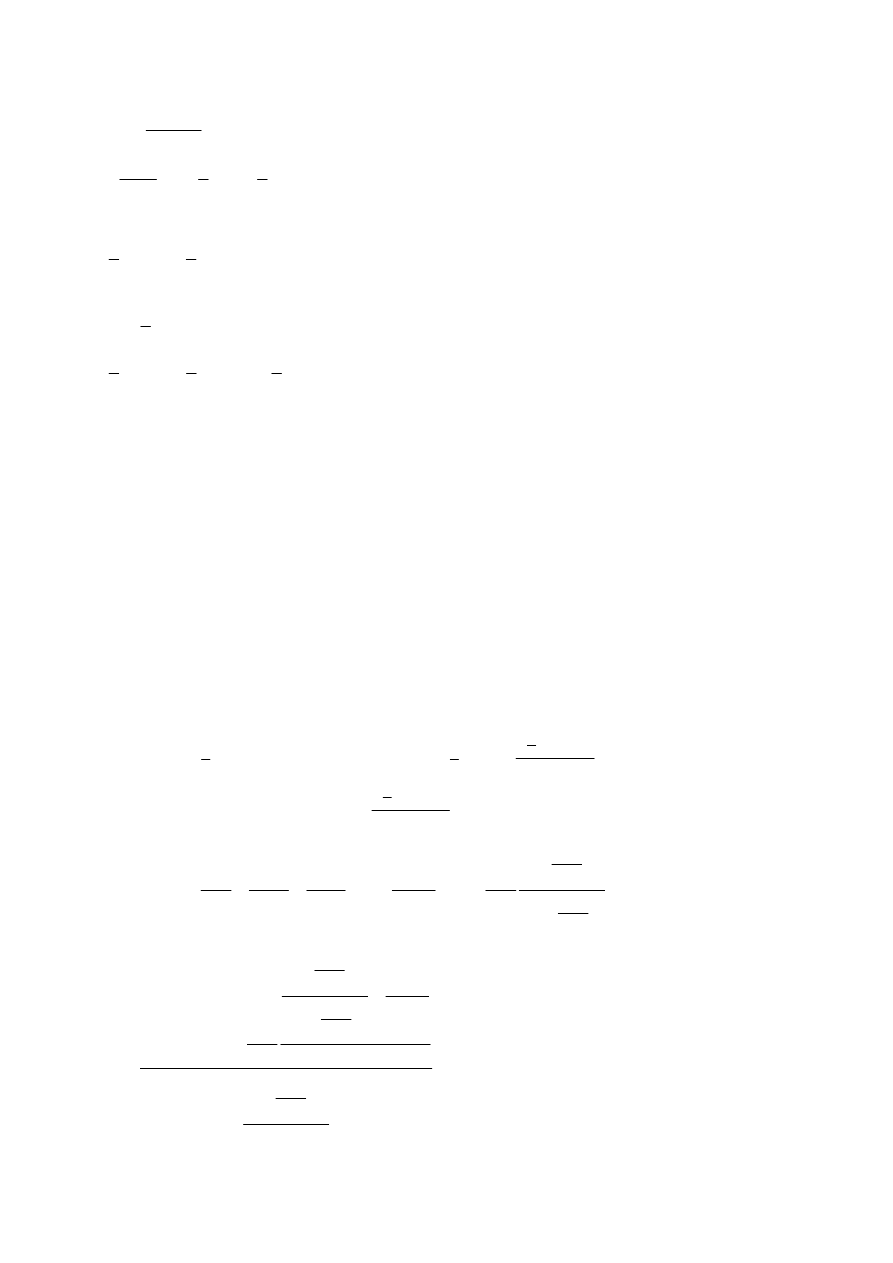
1
)
(
3
)
(
1
)
(
=
+
′
t
A
t
A
t
A
∫
+
=
+
A
A
dA
A
A
3
1
ln
3
1
3
1
∫
+
=
C
t
dt
1
C
t
t
A
t
A
+
=
+
)
(
3
1
)
(
ln
3
1
A(0)=1
3
1
=
C
3
1
)
(
3
1
)
(
ln
3
1
+
=
+
t
t
A
t
A
1
3
)
(
)
(
ln
+
=
+
t
t
A
t
A
i sprawdzamy
A(1)=2,8 L równa się około 3,82
A(1)=2,9 to L równa się około 3,96
A(1)=3 to L równa się około 4,09
Czyli odpowiedź B jest najbliżej
Zadanie 7
15
3
2
)
500
14
(
...
)
500
2
(
)
500
(
100000
v
P
v
P
v
P
Pv
⋅
−
+
+
⋅
−
+
−
+
=
15
3
2
15
...
3
2
100000
Qv
Qv
Qv
Qv
+
+
+
+
=
15
14
3
2
2
1
,
1
...
1
,
1
1
,
1
100000
v
R
v
R
v
R
Rv
⋅
+
+
⋅
+
⋅
+
=
(
)
i
v
a
v
Pa
v
v
v
v
Pa
14
14
15
14
2
15
14
500
14
...
2
500
100000
−
−
=
+
+
+
−
=
&
&
(
)
i
v
a
Q
v
v
v
Q
15
15
15
2
15
15
...
2
100000
−
=
+
+
+
=
&
&
07
,
1
1
,
1
1
07
,
1
1
,
1
1
07
,
1
1
07
,
1
1
,
1
...
07
,
1
1
,
1
07
,
1
1
,
1
07
,
1
1
100000
15
15
14
3
2
2
−
−
⋅
=
+
+
+
+
=
R
R
07
,
0
07
,
1
1
1
07
,
0
07
,
1
14
07
,
1
1
1
07
,
1
1
1
07
,
1
1
500
100000
15
14
14
−
−
−
−
⋅
+
=
P
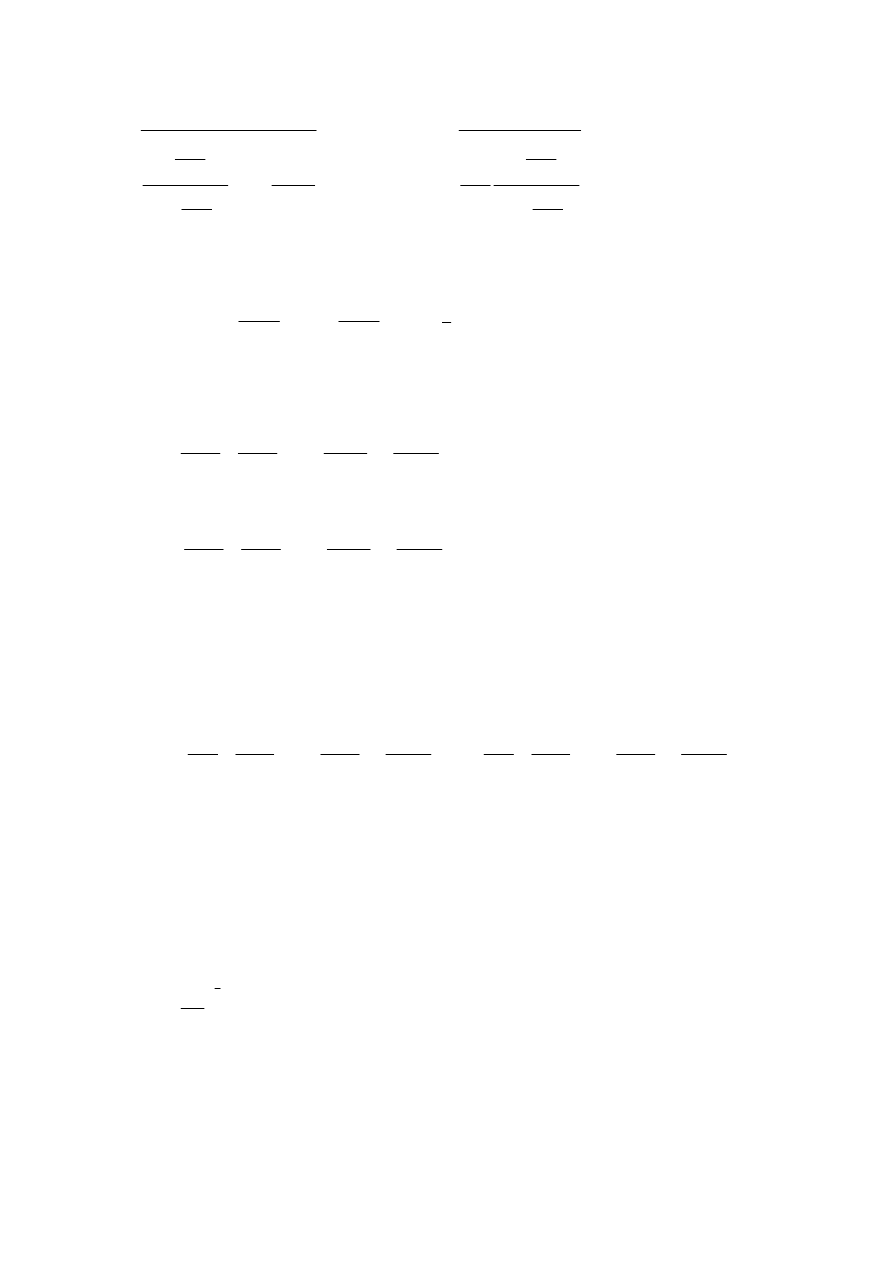
15
15
07
,
1
1
15
07
,
1
1
1
07
,
1
1
1
07
,
0
100000
⋅
−
−
−
⋅
=
Q
07
,
1
1
,
1
1
07
,
1
1
,
1
1
07
,
1
1
100000
15
−
−
=
R
Z tego:
235760
300000
15
2
15
1
14
2
14
1
500
15
15
≈
−
+
⋅
+
+
⋅
+
−
=
Rs
Q
P
ODP
Zadanie 8
Cena obligacji 10-letniej:
10
10
4
2
06
,
1
10800
06
,
1
1
...
06
,
1
1
06
,
1
1
800
1
+
+
+
+
=
P
cena obligacji 12-letniej:
12
12
4
2
06
,
1
10800
06
,
1
1
...
06
,
1
1
06
,
1
1
800
2
+
+
+
+
=
P
KREDYT=0,8(P1+P2)
Wartość kredytu po 3 latach:
3
08
,
1
)
2
1
(
8
,
0
)
3
(
⋅
+
=
P
P
KR
cena sprzedaży obligacji:
9
9
3
7
7
3
05
,
1
10800
05
,
1
1
...
05
,
1
1
05
,
1
1
800
05
,
1
10800
05
,
1
1
...
05
,
1
1
05
,
1
1
800
+
+
+
+
+
+
+
+
+
=
CO
wartość funduszu po 3 latach:
07
,
1
1600
⋅
=
F
RO – inwestycja
R1 – zwrot
RO=0,2(P1+P2)
R1=CO+F-KR(3)
100
1
0
1
3
1
⋅
−
=
R
R
ODP

3
9
2
10
7
2
8
08
,
1
)
2
1
(
8
,
0
07
,
1
1600
05
,
1
10800
05
,
1
1
1
05
,
1
1
1
05
,
1
800
05
,
1
10800
05
,
1
1
1
05
,
1
1
1
05
,
1
800
1
P
P
R
+
−
⋅
+
+
−
−
+
+
−
−
=
%
7
,
8
%
82
,
8
≈
≈
ODP
Zadanie 9
m – moment pierwszej raty
n – moment ostatniej raty
1.załóżmy, że
∞
=
n
, wtedy:
...
...
)
1
(
)
(
1
1
+
+
+
+
+
=
+
+
m
m
m
m
v
v
v
m
mv
a
d
v
v
v
mv
LICZ
v
v
mv
v
v
mv
v
LICZ
v
m
mv
v
LICZ
v
m
mv
LICZ
m
m
m
m
m
m
m
m
m
m
m
−
−
+
=
−
+
=
+
+
+
=
−
⋅
+
+
+
=
⋅
+
+
+
=
+
+
+
+
+
+
+
1
1
1
...
)
1
(
...
)
1
(
...
)
1
(
1
1
2
1
2
1
1
v
v
MIAN
m
−
=
1
v
v
m
a
d
−
+
=
1
)
(
wtedy:
∞
=
=
→
→
)
(
lim
)
(
lim
1
0
a
d
a
d
v
i
z tego wynika, że n – skończone
WTEDY:
n
m
m
m
n
m
m
m
v
v
v
v
n
m
v
m
mv
a
d
+
+
+
+
+
+
+
+
+
+
+
+
=
...
)
(
...
)
1
(
)
(
1
1
1
1
1
1
1
2
1
1
)
(
1
1
)
(
...
)
1
(
)
(
...
)
1
(
)
(
...
)
1
(
+
+
+
+
+
+
+
+
+
+
+
+
+
+
−
−
−
+
=
+
−
+
+
+
=
−
⋅
+
+
+
+
+
=
⋅
+
+
+
+
+
=
n
m
n
m
m
n
m
n
m
m
m
n
m
m
m
n
m
m
m
v
n
m
v
v
v
mv
v
n
m
v
v
mv
v
LICZ
v
n
m
v
m
mv
v
LICZ
v
n
m
v
m
mv
LICZ
v
v
n
m
v
v
v
v
mv
LICZ
n
m
n
m
m
−
+
−
−
−
+
−
=
+
+
+
1
)
(
)
1
(
1
1
1
2
1
v
v
v
MIAN
n
m
−
−
=
+
1
1
1
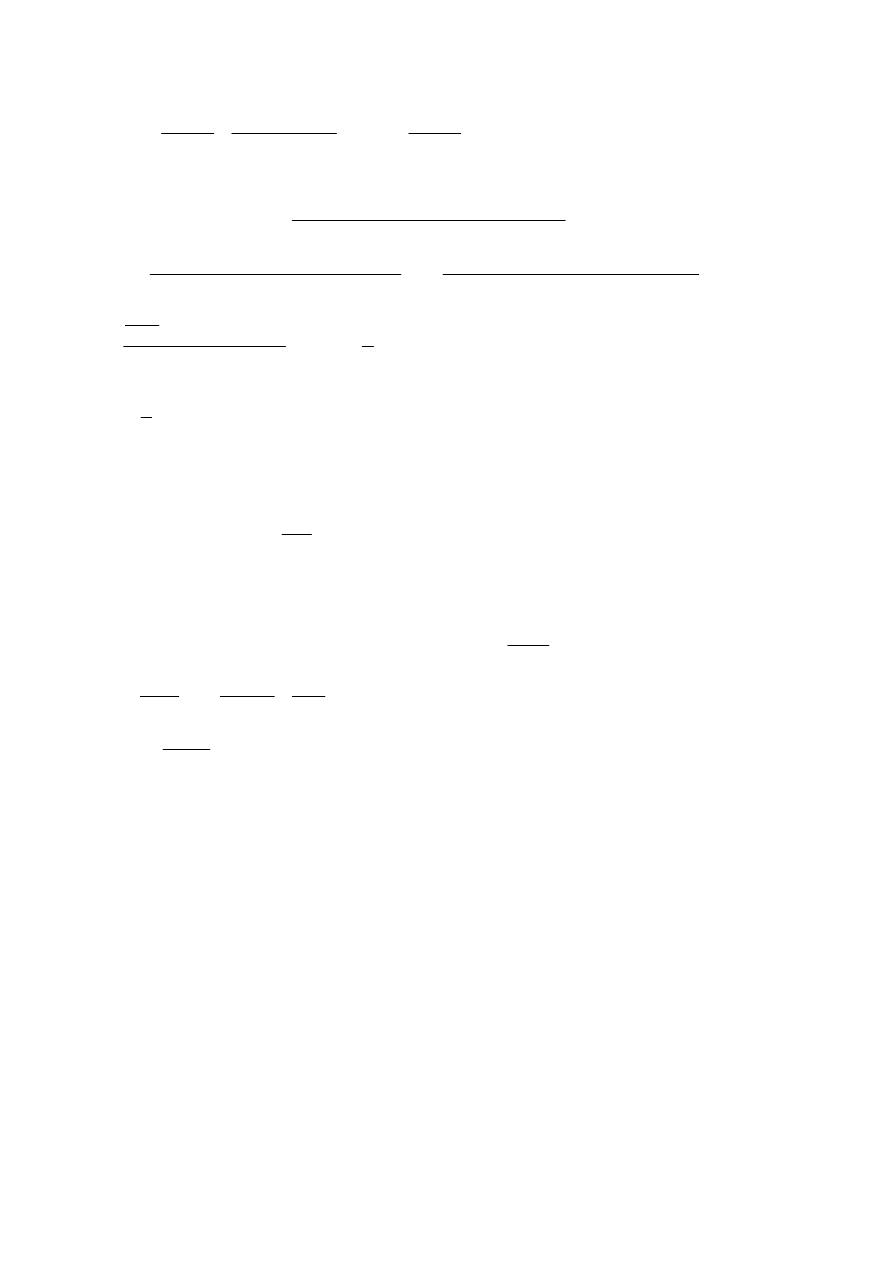
(
)
(
)
1
1
1
1
1
)
(
)
1
(
1
1
1
)
(
+
+
+
+
−
+
−
−
−
−
+
−
=
n
n
n
n
n
v
v
n
m
v
v
v
v
v
m
a
d
11
)
(
lim
)
(
lim
0
=
=
=
→
∞
→
m
a
d
a
d
v
i
(
)
(
)
=
−
−
−
+
−
−
+
−
=
=
+
+
→
→
→
)
1
(
1
)
1
)(
(
1
)
1
(
lim
)
(
lim
)
(
lim
1
1
1
1
0
v
v
v
v
n
m
v
v
v
m
a
d
a
d
n
n
n
v
v
i
(
)
=
+
−
+
+
−
+
+
+
=
−
+
−
+
+
+
+
=
−
→
+
+
−
→
n
n
n
v
H
n
n
n
v
v
n
v
n
n
m
nv
v
v
v
n
m
v
v
v
m
)
1
(
)
1
)(
(
...
2
1
lim
1
)
(
...
1
lim
1
1
1
1
1
1
5
,
20
2
)
1
(
)
1
)(
(
2
1
=
−
+
=
+
−
+
+
−
+
=
n
n
m
n
n
n
m
n
n
19
41
22
5
,
20
2
1
11
=
=
+
=
+
n
n
n
08
,
1
1
...
30
11
=
+
+
=
v
v
v
A
v
v
v
v
v
v
v
B
v
v
v
v
v
v
v
v
v
v
v
B
v
v
v
Bv
v
v
v
B
−
−
−
−
−
−
=
−
−
−
−
=
−
−
−
−
−
=
−
+
+
+
=
+
+
+
=
1
6
)
1
(
1
1
15
6
1
1
15
6
...
15
)
1
(
6
...
14
15
6
...
14
15
21
2
9
12
11
21
9
12
11
21
20
13
12
11
21
13
12
20
12
11
v
v
v
A
−
−
=
1
1
20
11
39
≈
+
B
A
Zadanie 10
SP(i) – spłacony kapitał w racie i-tej
KR(i) – kredyt dla i=0,1,...,10
ODP=KR(4)-KR(7)
3
2
6
2
10
...
9
8
)
7
(
10
...
6
5
)
4
(
v
v
v
KR
v
v
v
KR
+
+
+
=
+
+
+
=
=
+
+
+
−
−
−
=
−
−
−
+
+
+
=
6
5
4
3
2
3
2
6
2
10
9
8
3
3
3
10
9
8
10
...
6
5
v
v
v
v
v
v
v
v
v
v
v
v
ODP
(
) (
)
3
2
3
2
3
3
10
9
8
v
v
v
v
v
v
v
+
+
−
+
+
=

(
)
v
v
v
v
v
v
v
v
v
v
A
v
v
v
v
v
v
v
v
v
v
A
v
v
v
Av
v
v
v
A
−
−
+
+
=
−
−
+
+
=
−
−
−
+
=
−
+
+
=
−
+
+
=
+
+
=
1
10
8
1
10
)
1
(
8
10
1
1
8
10
8
)
1
(
10
9
8
10
9
8
4
3
2
4
2
4
2
2
4
3
2
4
3
2
3
2
(
)
(
)
=
+
−
−
+
−
+
+
=
i
i
v
v
i
i
v
v
v
v
v
ODP
)
1
(
1
3
)
1
(
10
8
3
4
3
2
3
(
) (
)
[
] [
]
=
+
−
−
+
+
=
−
−
−
+
+
=
3
6
5
4
3
3
3
2
3
3
3
10
8
1
1
3
10
8
1
v
v
v
v
v
i
v
v
v
v
v
i
(
)
[
]
(
)
[
]
=
⋅
−
+
−
+
+
=
−
+
−
+
+
=
i
v
v
v
v
v
v
v
v
v
i
1
3
11
11
3
3
10
8
1
3
3
2
3
3
2
3
(
)
(
)
[
]
(
)
(
)
(
)
[
]
=
⋅
−
+
+
−
+
+
+
=
⋅
−
+
+
−
+
+
+
=
i
v
v
v
v
v
v
v
i
v
v
v
v
v
v
v
1
3
1
)
1
(
11
1
1
3
1
)
1
(
11
2
2
3
2
3
2
3
(
)
(
)
[
]
(
)
(
)
[
]
=
⋅
−
−
+
+
+
=
⋅
−
−
+
+
+
=
i
i
v
v
v
v
i
v
v
v
v
v
1
3
10
11
)
1
(
1
3
)
1
(
11
1
3
2
3
2
3
[
]
i
i
a
v
1
3
)
1
11
(
3
3
⋅
−
+
=
Wyszukiwarka
Podobne podstrony:
2008.12.15 matematyka finansowa
2008 12 15
2003.12.06 matematyka finansowa
2008.06.02 matematyka finansowa
2008 12 15 prawdopodobie stwo i statystykaid 26466
2008 03 17 matematyka finansowaid 26447
2010.12.13 matematyka finansowa
1 2000.01.15 matematyka finansowa
2008.10.06 matematyka finansowa
2000.12.09 matematyka finansowa
2008.12.15 prawdopodobie stwo i statystyka
mat fiz 2008 12 15 id 282360 Nieznany
2010 03 15 matematyka finansowaid 26987
2002.06.15 matematyka finansowa
2008.03.17 matematyka finansowa
2008 12 15 praid 26465 Nieznany
2005 12 05 matematyka finansowaid 25347
2008 06 02 matematyka finansowaid 26453
więcej podobnych podstron