Egzamin dla Aktuariuszy z 20 czerwca 2011 r.
Matematyka Finansowa
Zadanie 1
2
1
, S
S
- cena spot baryłki ropy odpowiednio obecna i w grudniu 2011
2
1
, F
F
- cena futures baryłki oleju odpowiednio obecna i w grudniu 2011
h – liczba kontraktów futures (szukana odpowiedź)
minimalizujemy wariancję ekspozycji czyli:
(
)
(
)
(
)
42000
2000000
2000000
42000
2000000
1
2
1
2
1
1
2
2
⋅
⋅
−
−
⋅
−
+
=
⋅
⋅
−
−
=
h
F
F
S
S
S
h
F
F
S
Y
1
S
jest stałe i
F
F
F
S
S
S
∆
=
−
∆
=
−
1
2
1
2
,
Minimalizujemy więc wariancję
42000
2000000
⋅
⋅
∆
−
∆
⋅
=
h
F
S
X
S
∆
- zmiana ceny spot ropy a wiemy, że
( )
2
2
2
1
2
2
1
170
31
,
0
31
,
0
var
31
,
0
var
⋅
=
=
∆
→
=
∆
S
S
S
S
Analogicznie:
( )
2
2
2
1
5
,
167
23
,
0
var
23
,
0
var
⋅
=
∆
→
=
∆
F
F
F
(
)
89
,
0
,
,
1
1
=
∆
∆
=
∆
∆
S
F
S
S
F
F
ρ
ρ
(
) (
)
( )
( )
170
31
,
0
5
,
167
23
,
0
89
,
0
var
var
,
,
cov
⋅
⋅
⋅
⋅
=
∆
∆
⋅
∆
∆
=
∆
∆
S
F
S
F
S
F
ρ
( )
( )
(
)
→
∆
∆
⋅
⋅
⋅
−
⋅
∆
+
∆
=
S
F
h
F
h
S
X
,
cov
42000
4000000
42000
var
var
2000000
var
2
2
2
(
)
( )
(
)
( )
=
∆
∆
∆
=
⋅
∆
∆
∆
=
→
F
S
F
F
S
F
h
var
42000
,
cov
2000000
42000
var
2
,
cov
4000000
min
58
42000
5
,
167
23
,
0
170
31
,
0
5
,
167
23
,
0
89
,
0
2000000
2
2
≈
⋅
⋅
⋅
⋅
⋅
⋅
⋅
=
Zadanie 2
R – stopa zwrotu
R
f
st
R
R
β
+
=
f
R - stopa wolna od ryzyka
R
st
- risk premium
Dla I portfela:
08135
,
0
031
,
0
85
,
0
055
,
0
=
⋅
+
=
R
(nie uwzględniamy dodatkowej premii)
Lub
(
)
0839
,
0
003
,
0
031
,
0
85
,
0
055
,
0
=
+
⋅
+
=
R
(uwzględniamy dodatkową premię za ryzyko)
Dla portfela II:
08084
,
0
038
,
0
68
,
0
055
,
0
=
⋅
+
=
R
Jak widać w obu przypadkach stopa zwrotu portfela I jest większa od stopy portfela II

Zadanie 3
i
p - prawdopodobieństwo wypłacalności w i-tym roku
konca
do
osc
wyplacaln
sie
utrzyma
ze
bienstwo
prawdopodo
-
1
32
,
0
75
,
0
85
,
0
9
,
0
25
,
0
85
,
0
9
,
0
15
,
0
9
,
0
1
,
0
4
3
2
1
5
4
3
2
1
p
p
p
p
p
p
p
p
p
−
−
−
−
=
⋅
⋅
⋅
=
⋅
⋅
=
⋅
=
=
055
,
1
150000
3
,
0
1
⋅
=
w
2
2
055
,
1
150000
3
,
0
055
,
1
150000
065
,
0
⋅
+
⋅
=
w
3
2
3
055
,
1
150000
3
,
0
055
,
1
150000
065
,
0
055
,
1
150000
065
,
0
⋅
+
⋅
+
⋅
=
w
4
3
2
4
055
,
1
150000
3
,
0
055
,
1
150000
065
,
0
055
,
1
150000
065
,
0
055
,
1
150000
065
,
0
⋅
+
⋅
+
⋅
+
⋅
=
w
4
4
3
2
5
055
,
1
150000
055
,
1
1
055
,
1
1
055
,
1
1
055
,
1
1
150000
065
,
0
+
+
+
+
⋅
=
w
93816
5
5
4
4
3
3
2
2
1
1
≈
+
+
+
+
=
w
p
w
p
w
p
w
p
w
p
ODP
Zadanie 4
Gdy
(
)
+
=
→
≅
2
2
2
1
exp
,
σ
σ
w
Ee
w
N
X
X
Przy braku arbitrażu:
( )
(
)
09
,
0
;
0
3
,
0
bo
)
1
(
)
1
(
)
1
(
)
1
(
)
0
(
005
,
0
045
,
0
05
,
0
3
,
0
05
,
0
05
,
0
N
Z
e
A
e
e
A
e
E
A
e
ES
e
S
Z
≅
=
=
=
=
−
−
−
−
Z
e
e
S
S
e
S
A
3
,
0
005
,
0
005
,
0
)
0
(
)
1
(
)
0
(
)
1
(
=
→
=
→
( )
=
=
=
=
−
−
−
05
,
0
6
,
0
01
,
0
05
,
0
2
6
,
0
01
,
0
2
05
,
0
2
2
)
0
(
)
0
(
)
0
(
)
1
(
e
e
E
e
e
S
e
e
S
E
e
S
S
E
ODP
Z
Z
(
)
14
,
0
05
,
0
36
,
0
5
,
0
01
,
0
36
,
0
;
0
6
,
0
e
e
e
e
N
Z
=
=
≅
=
−
⋅
Zadanie 5
st(AA) – stan, że na początku roku 2 rating A i na początku roku 3 rating A
st(AB), st(BA), st(BB) – analogicznie
BB
BA
AB
AA
p
p
p
p
,
,
,
- odpowiednie prawdopodobieństwa
BB
BA
AB
AA
w
w
w
w
,
,
,
- odpowiednie wartości obligacji
49
,
0
7
,
0
2
=
=
AA
p
21
,
0
3
,
0
7
,
0
=
⋅
=
AB
p
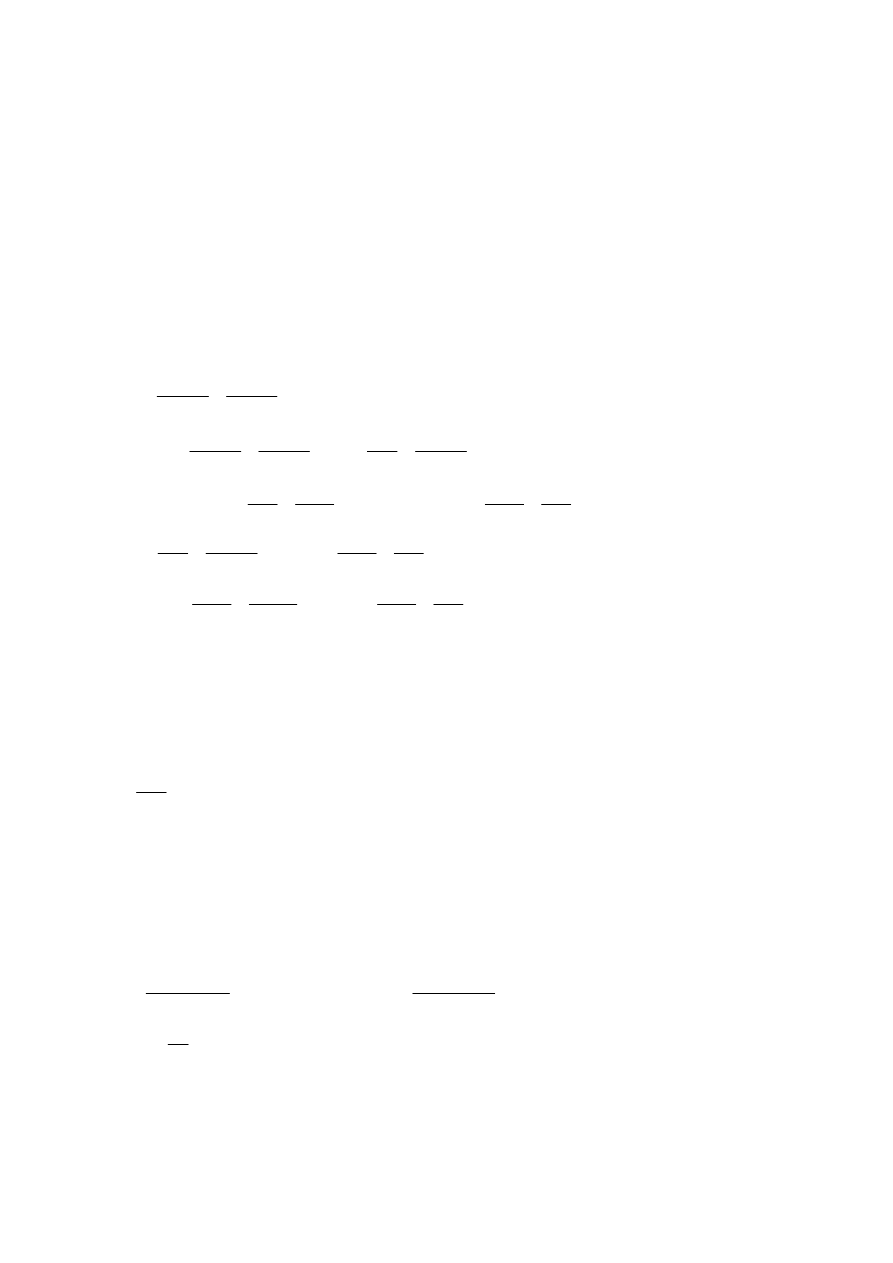
03
,
0
1
,
0
3
,
0
=
⋅
=
BA
p
27
,
0
9
,
0
3
,
0
=
⋅
=
BB
p
1050
9
,
0
50
9
,
0
50
9
,
0
3
2
⋅
+
⋅
+
⋅
=
AA
w
1050
8
,
0
9
,
0
50
9
,
0
50
9
,
0
2
2
⋅
⋅
+
⋅
+
⋅
=
AB
w
1050
9
,
0
8
,
0
9
,
0
50
8
,
0
9
,
0
50
9
,
0
⋅
⋅
⋅
+
⋅
⋅
+
⋅
=
BA
w
1050
8
,
0
9
,
0
50
8
,
0
9
,
0
50
9
,
0
2
⋅
⋅
+
⋅
⋅
+
⋅
=
BB
w
81
,
785
≈
⋅
+
⋅
+
⋅
+
⋅
=
BB
BB
BA
BA
AB
AB
AA
AA
w
p
w
p
w
p
w
p
ODP
Zadanie 6
3
2
)
1
(
200
)
1
(
5
i
i
P
+
−
+
−
=
′
∫
+
+
+
+
=
+
+
−
+
−
=
C
i
i
C
i
i
i
P
2
3
2
)
1
(
100
1
5
)
1
(
200
)
1
(
5
)
(
03
,
1
5
03
,
1
100
83
,
103
03
,
1
100
03
,
1
5
83
,
103
)
03
,
0
(
2
2
−
−
=
→
+
+
=
=
C
C
P
03
,
1
5
03
,
1
100
83
,
103
)
1
(
100
1
5
)
(
2
2
−
−
+
+
+
+
=
i
i
i
P
85
,
102
03
,
1
5
03
,
1
100
83
,
103
035
,
1
100
035
,
1
5
)
035
,
0
(
2
2
≈
−
−
+
+
=
P
Zadanie 7
A
x
- udział obligacji A
B
A
n
n ,
- długości obligacji
B
A
N
N ,
- nominały
06
,
1
1
=
v
(
)
A
A
n
n
v
v
v
I
05
,
1
...
05
,
0
9161
,
0
.
+
+
+
=
(
)
A
A
n
A
n
A
v
n
v
n
v
v
II
05
,
1
...
2
05
,
0
168
,
9
9161
,
0
.
2
+
+
+
+
=
⋅
(
)
B
B
n
n
v
v
v
III
07
,
1
...
07
,
0
0736
,
1
.
+
+
+
=
(
)
B
B
n
B
n
B
v
n
v
n
v
v
IV
07
,
1
...
2
07
,
0
0736
,
1
611
,
7
.
2
+
+
+
+
=
⋅
B
obligacji
ilosc
-
0736
,
1
1
A;
obligacji
ilosc
-
9161
,
0
⋅
−
=
⋅
=
B
A
B
A
A
A
N
x
c
N
x
c
M
L
=
579
,
7
, gdzie
(
)
(
)
(
)
[
]
+
−
+
−
+
+
+
=
−
−
1
1
2
1
05
,
1
1
...
2
05
,
0
A
A
n
A
n
A
A
A
v
n
v
n
v
v
N
c
L
(
)
(
)
(
)
[
]
1
1
2
1
07
,
1
1
...
2
07
,
0
−
−
−
+
−
+
+
+
+
B
B
n
B
n
B
B
B
v
n
v
n
v
v
N
c
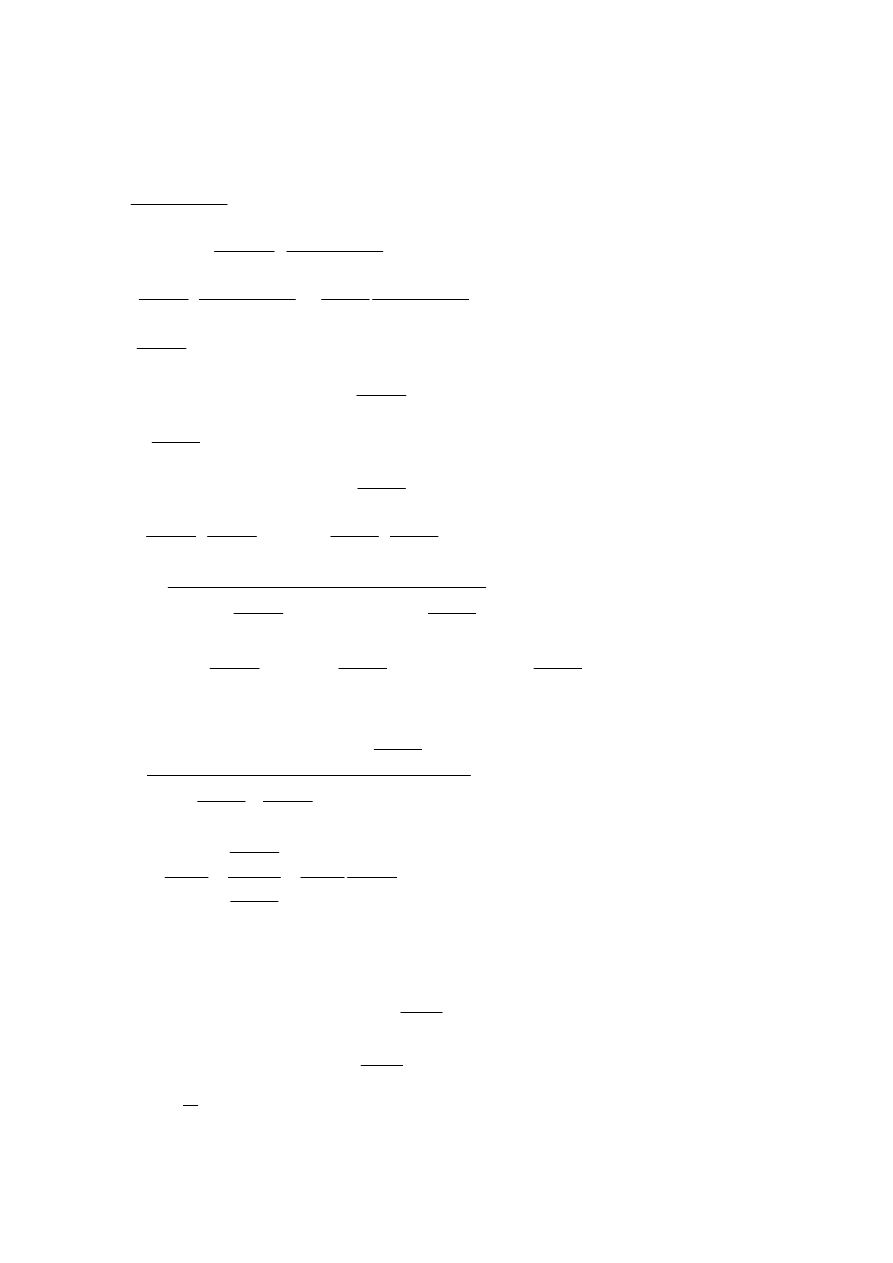
(
)
[
]
(
)
[
]
1
1
1
1
07
,
1
...
07
,
0
05
,
1
...
05
,
0
−
−
−
−
+
+
+
+
+
+
+
=
B
B
A
A
n
n
B
B
n
n
A
A
v
v
v
N
c
v
v
v
N
c
M
(
)
(
)
(
)
→
−
+
−
+
+
+
=
−
⋅
−
A
A
n
A
n
A
v
n
v
n
v
v
I
II
1
05
,
1
1
...
2
05
,
0
9161
,
0
9161
,
0
168
,
9
:
3
2
(
)
(
)
(
)
1
1
2
1
05
,
1
1
...
2
05
,
0
168
,
8
9161
,
0
−
−
−
+
−
+
+
+
=
⋅
→
A
A
n
A
n
A
v
n
v
n
v
v
v
Analogicznie:
(
)
(
)
(
)
1
1
2
1
07
,
1
1
...
2
07
,
0
0736
,
1
611
,
6
:
−
−
−
+
−
+
+
+
=
⋅
−
B
B
n
B
n
B
v
n
v
n
v
v
v
v
III
IV
v
x
v
x
L
A
A
0736
,
1
611
,
6
0736
,
1
1
168
,
8
9161
,
0
9161
,
0
⋅
−
+
⋅
=
z I:
(
)
1
1
05
,
1
...
1
05
,
0
9161
,
0
−
−
+
+
+
=
A
A
n
n
v
v
v
(
)
05
,
0
9161
,
0
05
,
1
...
05
,
0
1
1
−
=
+
+
+
→
−
−
v
v
v
v
A
A
n
n
Z III:
(
)
1
1
07
,
1
...
1
07
,
0
0736
,
1
−
−
+
+
+
=
B
B
n
n
v
v
v
(
)
07
,
0
0736
,
1
07
,
1
...
07
,
0
1
1
−
=
+
+
+
→
−
−
v
v
v
v
B
B
n
n
−
−
+
−
=
07
,
0
0736
,
1
0736
,
1
1
05
,
0
9161
,
0
9161
,
0
v
x
v
x
M
A
A
(
)
(
)
−
−
+
−
⋅
⋅
−
+
⋅
=
0736
,
1
07
,
0
06
,
1
1
9161
,
0
05
,
0
06
,
1
06
,
1
611
,
6
1
06
,
1
168
,
8
579
,
7
A
A
A
A
A
x
x
x
x
x
=
−
+
−
−
−
0736
,
1
07
,
0
06
,
1
579
,
7
0736
,
1
07
,
0
06
,
1
9161
,
0
05
,
0
06
,
1
579
,
7
A
x
(
)
611
,
6
06
,
1
611
,
6
06
,
1
06
,
1
168
,
8
⋅
+
⋅
−
⋅
=
A
x
(
)
611
,
6
168
,
8
06
,
1
9161
,
0
05
,
0
0736
,
1
07
,
0
579
,
7
0736
,
1
07
,
0
06
,
1
579
,
7
611
,
6
06
,
1
−
−
−
−
−
⋅
=
A
x
6
,
0
9161
,
0
0736
,
1
1
0736
,
1
1
9161
,
0
≈
−
=
−
=
=
A
A
A
A
B
B
A
A
x
x
x
x
N
c
N
c
ODP
Zadanie 8
Odsetki spłacone w I półroczu:
13000
400000
2
065
,
0
)
1
(
=
⋅
=
OD
Kredyt po roku
6
12
065
,
0
1
400000
)
1
(
+
=
K
12
/
065
,
0
;
360
)
1
(
Xa
K
=
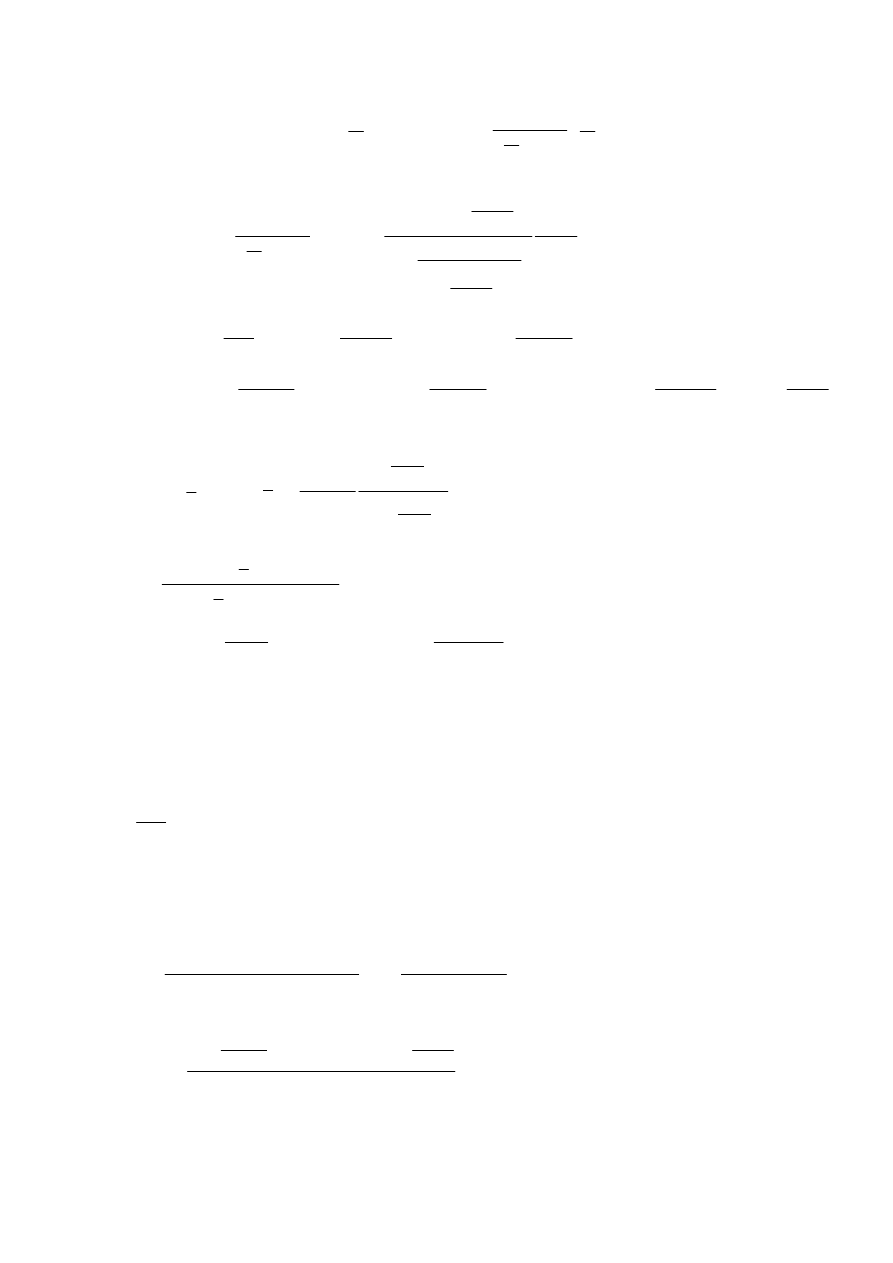
Kredyt po 120 ratach:
12
/
065
,
0
;
240
12
/
065
,
0
;
360
12
/
065
,
0
;
240
)
1
(
)
2
(
)
2
(
a
a
K
K
Xa
K
=
→
=
Raty zapłacone w 2 okresie:
12
065
,
0
12
065
,
0
1
1
1
12
065
,
0
1
400000
)
1
(
120
120
)
2
(
360
6
12
/
065
,
0
;
360
+
−
+
=
=
=
X
a
K
X
OD
+
+
+
+
+
+
+
+
+
+
=
60
2
)
1
(
1
)
60
(
...
)
1
(
1
)
2
(
1
1
)
(
)
2
(
i
A
X
i
A
X
i
A
X
K
12
065
,
0
gdzie
)
1
(
1
99
,
0
)
60
(
...
)
1
(
1
99
,
0
)
60
(
)
1
(
1
99
,
0
)
60
(
120
60
62
2
61
=
+
+
+
+
+
+
+
+
⋅
+
+
i
i
A
X
i
A
X
i
A
X
( )
(
)
A
X
i
i
i
Ia
A
Xa
K
B
i
i
60
1
99
,
0
1
1
99
,
0
1
)
1
(
99
,
0
)
2
(
60
61
;
60
;
60
+
+
−
+
−
+
+
+
=
4
4
4
3
4
4
4
2
1
B
Ia
BX
Xa
K
A
60
)
(
)
2
(
12
/
065
,
0
;
60
12
/
065
,
0
;
60
+
−
−
=
→
99
,
0
1
99
,
0
1
99
,
0
)
60
(
60
2
60
1
60
)
3
(
60
−
−
+
+
⋅
+
+
=
A
X
A
X
OD
6000
400000
015
,
0
)
4
(
=
⋅
=
OD
411000
400000
)
4
(
)
3
(
)
2
(
)
1
(
≈
−
+
+
+
=
OD
OD
OD
OD
ODP
Zadanie 9
K(i) – pozostały kredyt w i
05
,
1
1
=
v
+
+
+
+
+
+
+
=
6
2
)
19
(
...
)
15
(
)
14
(
)
14
(
v
X
R
v
X
R
v
X
R
K
16
8
7
)
9
(
...
)
17
(
)
18
(
v
X
R
v
X
R
v
X
R
+
+
+
+
+
+
+
15
7
6
5
2
)
9
(
...
)
17
(
)
18
(
)
19
(
...
)
16
(
)
15
(
)
15
(
v
X
R
v
X
R
v
X
R
v
X
R
v
X
R
v
X
R
K
+
+
+
+
+
+
+
+
+
+
+
+
+
=
(
)
X
R
K
K
X
R
K
K
X
R
ODP
14
)
15
(
)
14
(
1
14
)
15
(
)
14
(
14
+
−
−
=
+
−
−
+
=
16
15
7
6
5
2
)
9
(
...
...
)
15
(
)
14
(
v
X
R
Xv
Xv
Xv
Xv
Xv
Xv
K
K
+
+
+
+
+
+
−
−
−
−
=
−
=
+
−
−
−
+
+
−
−
−
=
X
R
v
v
Xv
v
X
R
v
v
Xv
ODP
14
1
1
)
9
(
1
1
1
5
16
10
6

(
)
%
56
14
7
,
16
9
7
,
16
1
2
1
14
9
1
1
16
16
6
16
6
16
6
≈
+
+
+
−
−
−
−
=
+
+
+
−
+
−
−
−
=
v
v
v
v
v
X
R
v
X
R
v
v
v
v
v
Zadanie 10
∑
∞
=
+
+
=
0
2
3
)
2
)(
1
(
1
n
n
n
v
n
n
ODP
)
2
)(
1
(
2
)
(
)
2
)(
1
(
)
1
(
)
2
(
2
1
)
2
)(
1
(
1
+
+
+
+
+
=
+
+
+
+
+
=
+
+
+
=
+
+
n
n
B
A
n
B
A
n
n
n
B
A
n
n
B
n
A
n
n
2
1
1
1
)
2
)(
1
(
1
1
1
1
2
0
+
−
+
=
+
+
→
−
=
=
→
=
+
=
+
n
n
n
n
B
A
B
A
B
A
3
:
2
v
x
OZNACZENIE
=
∑
∞
=
=
+
−
+
−
+
−
=
+
−
+
=
0
2
....
4
1
3
1
3
1
2
1
2
1
1
2
1
1
1
n
n
x
x
x
n
n
ODP
=
+
+
−
+
+
+
=
...
4
1
3
1
...
3
1
2
1
2
1
2
2
x
x
x
x
=
+
+
−
+
+
+
=
...
4
1
3
1
1
...
3
1
2
1
1
2
1
4
3
2
3
2
x
x
x
x
x
x
−
−
−
−
+
=
∑
∑
∞
=
∞
=
1
2
2
1
2
1
1
1
1
1
2
1
k
k
k
k
x
x
x
k
x
x
x
k
x
∑
∞
=
=
1
1
)
(
k
k
x
k
x
f
∑
∫
∞
=
−
=
→
=
+
−
−
=
−
=
→
−
=
=
′
1
1
0
0
)
0
(
ale
)
1
ln(
1
1
)
(
1
1
)
(
k
k
C
f
C
x
x
x
f
x
x
x
f
∑
∞
=
−
−
=
=
1
)
1
ln(
1
)
(
k
k
x
x
k
x
f
=
+
+
−
+
−
−
−
=
x
x
x
x
x
ODP
1
2
1
)
1
ln(
1
1
)
1
ln(
1
2
1
2
(
)
3
gdzie
)
1
ln(
1
)
1
ln(
1
1
2
2
v
x
x
x
x
x
=
−
+
−
−
=
56
,
0
≈
ODP
Wyszukiwarka
Podobne podstrony:
2011.06.20 matematyka finansowa
2011 06 20 Dec nr 230 MON Gosp mieniem Skarbu Państwa
2001 06 02 matematyka finansowaid 21606
mechanika egzamin MT-2011-06-20-termin1
2008.06.02 matematyka finansowa
2011.06.20 prawdopodobie stwo i statystyka
2001.06.02 matematyka finansowa
2006.03.20 matematyka finansowa
2006 06 05 matematyka finansowaid 25460
2002.06.15 matematyka finansowa
1 2000 06 17 matematyka finansowaid 8918
2011 04 04 matematyka finansowaid 27338
2011 06 20 prawdopodobie stwo i statystykaid 27374
2008 06 02 matematyka finansowaid 26453
2002 06 15 matematyka finansowaid 21641
2011 06 20 Dec nr 230 MON Gosp mieniem Skarbu Państwa
2001 06 02 matematyka finansowaid 21606
więcej podobnych podstron