Egzamin dla Aktuariuszy z 4 kwietnia 2011 r.
Matematyka Finansowa
Zadanie 1
(
)
(
)
(
)
(
)
1500
)
1
)(
2
(
)
1
(
)
1
(
2
2
2
1500
)
1
(
...
2
2
....
3
4
3
2
2
4
2
2
3
2
2
4
2
2
3
2
2
3
2
2
2
3
2
2
2
1
1
1
3
4
1
1
2
3
1
2
+
−
−
+
=
−
−
−
+
+
=
−
−
+
+
+
=
−
+
+
+
=
−
⋅
+
−
+
+
=
−
⋅
+
=
−
+
⋅
+
=
−
⋅
+
−
⋅
+
=
−
⋅
+
=
−
⋅
+
=
k
N
k
N
k
k
k
N
k
k
r
r
N
r
N
N
r
N
r
r
N
r
N
N
r
N
r
r
N
r
r
k
1498
)
1
(
2
+
+
−
+
=
N
k
N
k
r
k
2
1
2
dla
min
−
=
−
=
N
a
b
k
r
i N jest nieparzyste bo założenia
1500
)
1
(
2
+
−
=
N
r
N
1500
4
)
3
(
1500
2
2
1
2
2
1
4
1
2
1
2
1
2
2
min
+
−
−
=
+
−
−
−
−
+
=
−
−
−
−
+
=
N
N
N
N
N
N
N
r
196
4
)
1
(
1500
1500
)
1
(
2
3
=
−
+
−
+
−
N
N
56
3136
0
783
2
784
9
6
8
8
2
2
=
∆
=
∆
=
−
+
=
+
−
+
−
N
N
N
N
N
27
2
56
2
=
+
−
=
→
N
25
25
20
20
15
15
10
10
5
5
25
24
20
19
15
14
10
9
5
4
v
r
v
r
v
r
v
r
v
r
ODP
+
+
+
+
=
1500
1405
1500
19
5
1360
1500
14
10
1365
1500
9
15
1420
1500
4
20
25
20
15
10
5
=
=
+
⋅
−
=
=
+
⋅
−
=
=
+
⋅
−
=
=
+
⋅
−
=
r
r
r
r
r
3183
05
,
1
1
1500
25
24
05
,
1
1
1405
20
19
05
,
1
1
1360
15
14
05
,
1
1
1365
10
9
05
,
1
1
1420
5
4
25
20
15
10
5
≈
+
+
+
+
⋅
=
ODP
Zadanie 2
∑
∑
∑
∞
=
∞
=
∞
=
−
−
=
+
+
+
+
=
+
+
−
+
−
=
1
0
0
2
1
1
2
)
3
)(
1
(
!
2
1
)
2
(
)!
1
(
2
1
)
1
(
k
k
k
k
k
k
k
k
k
v
k
k
v
v
k
k
v
k
k
v
k
k
ODP
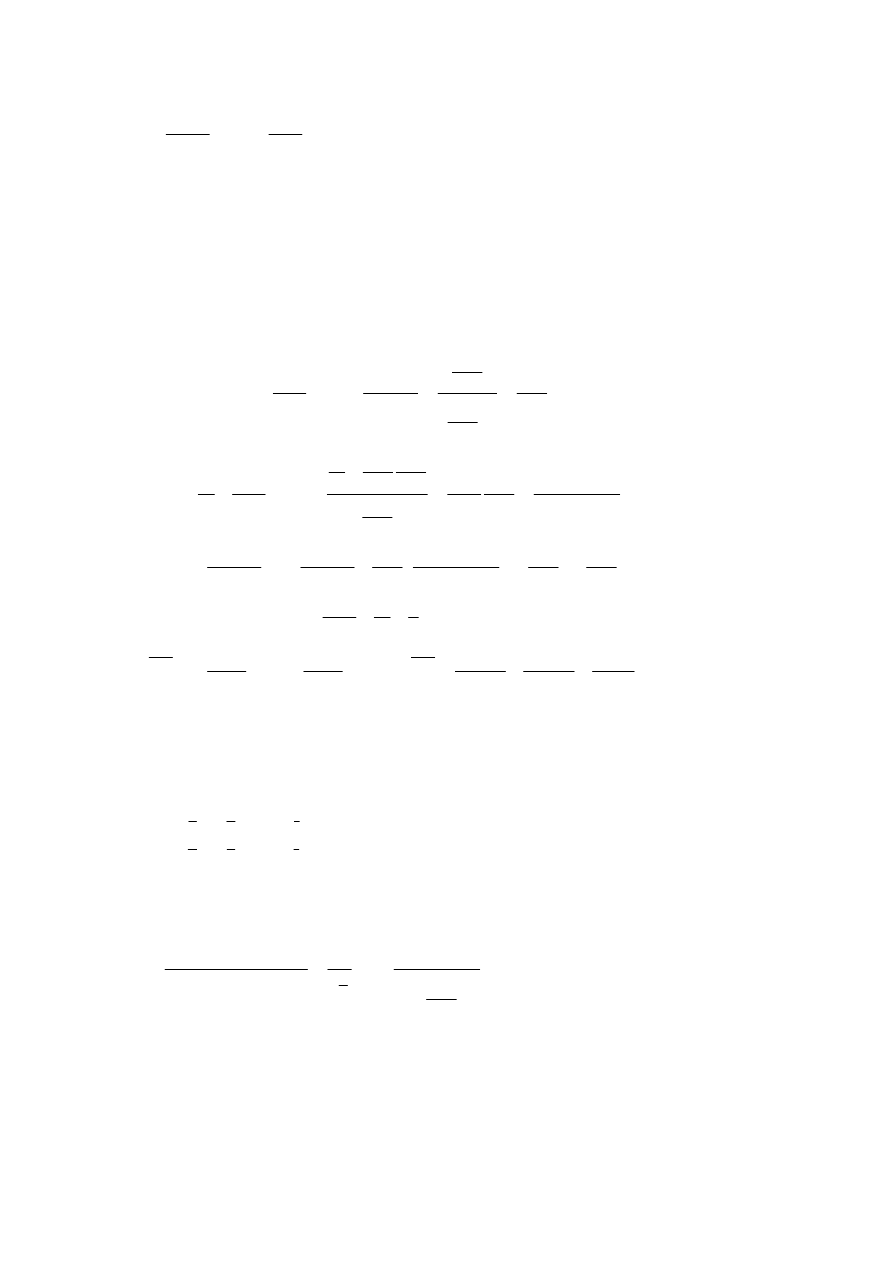
( )
(
)
∑
∑
∑
∞
=
∞
=
∞
=
+
+
+
+
=
0
0
0
2
2
3
4
!
2
1
!
5
,
0
k
k
k
k
k
k
k
k
v
k
k
v
v
k
v
k
k
(
)
(
)
(
)
....
....
2
2
...
)
1
1
2
(
1
0
2
...
1
2
1
)
1
(
...
2
1
...
2
1
2
3
2
2
2
2
2
2
3
2
2
2
2
2
2
+
+
+
+
+
=
+
+
⋅
+
+
⋅
=
+
−
+
=
−
+
+
=
+
+
=
v
v
v
v
v
v
v
v
v
X
v
v
Xv
v
v
X
2
2
2
2
3
2
2
1
1
1
1
)
1
(
1
...
)
1
(
...
2
...
2
i
i
i
i
i
v
v
Y
v
v
v
v
v
Y
v
v
Yv
v
v
Y
+
=
+
+
=
−
=
→
−
=
+
+
=
−
+
+
=
+
+
=
3
2
2
2
)
1
)(
2
(
1
2
1
1
1
1
2
1
1
2
)
1
(
i
i
i
i
i
i
i
i
i
i
i
i
i
X
v
v
i
v
X
+
+
=
+
+
=
+
+
+
+
=
→
−
+
=
−
∑
∑
∞
=
∞
=
=
+
+
+
+
+
+
+
+
+
=
0
0
2
3
2
1
3
1
4
)
1
)(
2
(
1
1
!
)
5
,
0
(
!
)
5
,
0
(
k
k
k
k
i
i
i
i
i
i
i
i
k
v
k
v
k
ODP
[
]
=
+
+
+
+
+
+
=
i
i
i
i
e
v
v
e
v
v
3
4
2
25
,
0
5
,
0
2
3
5
,
0
2
5
,
0
24486
045
,
0
3
045
,
0
4
045
,
0
045
,
2
045
,
1
1
25
,
0
045
,
1
1
5
,
0
2
3
045
,
1
1
5
,
0
2
045
,
1
1
5
,
0
≈
+
+
+
+
+
=
⋅
⋅
e
e
Zadanie 3
S – kwota spłaty z jednej raty kredytu
[
]
1
10
11
...
)
9
(
a
a
a
S
K
+
+
+
=
[
]
1
11
12
...
)
8
(
a
a
a
S
K
+
+
+
=
Na koniec 9 roku (po wpłacie) zostanie spłaconych 9 kredytów
Z tego wynika, że na koniec 9 roku kredytobiorca wpłaca 12S
[
]
51
,
0
1
07
,
1
1
1
07
,
0
12
1
12
)
9
(
)
8
(
)
9
(
)
8
(
12
12
12
≈
−
−
⋅
=
−
=
−
−
−
=
a
K
K
K
K
S
ODP
Zadanie 4
Z banku na koniec
05
,
1
500000
⋅
=
S
Na koniec każdego roku mamy kwotę
25000
05
,
0
500000
=
⋅
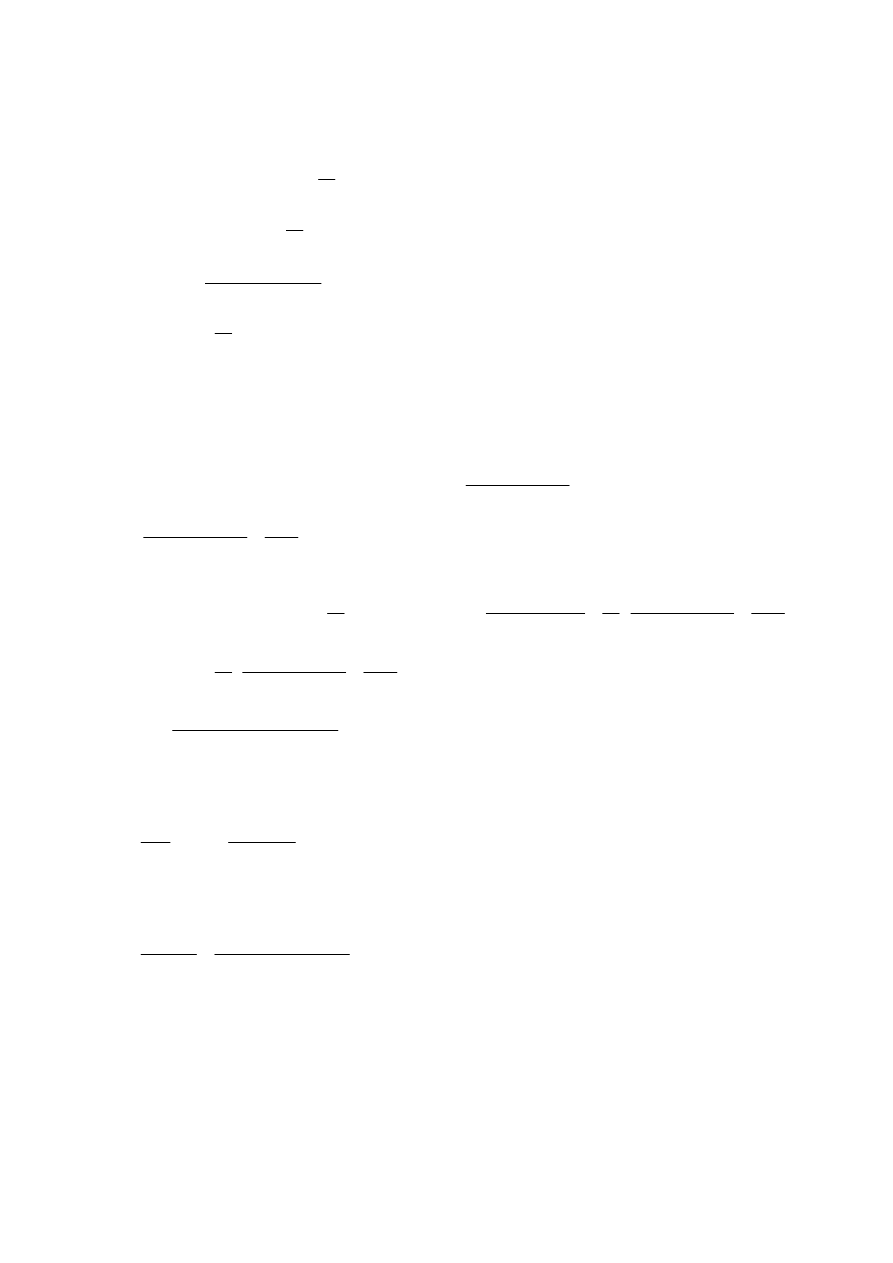
F(k) – kwota środków z k-tego funduszu na koniec 10 roku
[
]
055
,
1
...
055
,
1
25000
4
,
0
)
1
(
9
+
+
⋅
=
F
∑
=
−
−
−
=
9
1
10
06
,
1
11
1
)
4
,
0
1
(
25000
)
2
(
k
k
k
F
∑
=
−
⋅
−
=
9
1
10
07
,
1
11
)
4
,
0
1
(
25000
)
3
(
k
k
k
F
(
)
055
,
0
055
,
1
1
055
,
1
10000
)
1
(
9
−
=
F
4
4 3
4
4 2
1
X
k
k
k
F
∑
=
−
⋅
⋅
=
9
1
10
07
,
1
11
1
15000
)
3
(
(
)
(
)
10
07
,
1
07
,
0
07
,
1
1
07
,
1
07
,
1
9
07
,
1
...
07
,
1
07
,
1
1
07
,
1
07
,
1
9
...
07
,
1
2
07
,
1
07
,
1
07
,
1
9
...
07
,
1
2
07
,
1
10
2
9
10
2
9
10
8
9
⋅
−
−
=
⋅
−
+
+
+
=
−
⋅
+
+
⋅
+
=
⋅
⋅
+
+
⋅
+
=
X
X
X
(
)
07
,
0
7
,
10
07
,
0
07
,
1
1
07
,
1
2
10
−
−
=
X
(
)
(
)
−
−
−
−
=
⋅
−
=
∑
∑
=
=
−
−
06
,
0
6
,
10
06
,
0
06
,
1
1
06
,
1
11
1
06
,
0
06
,
1
1
06
,
1
15000
06
,
1
11
06
,
1
15000
)
2
(
2
10
9
9
1
9
1
10
10
k
k
k
k
k
F
(
)
−
−
⋅
=
07
,
0
7
,
10
07
,
0
07
,
1
1
07
,
1
11
1
15000
)
3
(
2
10
F
%
2
,
5
1
500000
)
3
(
)
2
(
)
1
(
1
,
0
≈
−
+
+
+
=
S
F
F
F
ODP
Zadanie 5
974
95
,
0
04
,
1
03
,
1
1080
95
,
0
03
,
1
70
2
≈
⋅
+
⋅
=
C
x – narzut
)
04
,
1
)(
03
,
1
(
1080
03
,
1
70
x
x
x
C
+
+
+
+
=
(
)
(
)
odpada
0
x
0
8
,
1152
0712
,
1
70
07
,
2
1080
70
8
,
72
07
,
2
0712
,
1
1080
)
04
,
1
(
70
)
04
,
1
)(
03
,
1
(
1947
2
2
<
→
=
−
+
−
⋅
+
+
+
=
+
+
+
+
=
+
+
≈
jeden
C
x
C
Cx
x
x
x
C
x
x
x
C
4
4 3
4
4 2
1
ODP wychodzi około 5,4%

Zadanie 6
2
)
1
(
1000
1
)
(
i
K
i
K
i
P
+
+
+
+
=
)
(
)
(
)
(
)
(
i
P
i
P
Convexity
i
P
i
P
ration
ModifiedDu
′′
=
′
−
=
3
,
1009
254
,
5
)
(
)
(
3
,
1009
855
,
1
⋅
=
′′
′
−
=
⋅
i
P
i
P
)
(
2
005
,
0
)
(
005
,
0
)
(
)
005
,
0
(
2
i
P
i
P
i
P
i
P
′′
+
′
−
=
−
z dokładnością do 0,001 (Taylor)
73
,
1018
3
,
1009
254
,
5
2
005
,
0
3
,
1009
855
,
1
005
,
0
3
,
1009
)
005
,
0
(
2
=
⋅
⋅
+
⋅
⋅
+
=
−
=
i
P
ODP
Zadanie 7
p – prawdopodobieństwo I stanu
1
q
p
i
2
3
1
,
2
5
1
,
2
=
+
+
=
+
=
qv
pv
qv
pv
v
I
II
v
pv
v
pv
7
3
,
6
4
2
1
,
2
4
1
,
2
=
→
−
→
⋅
+
=
+
=
9
1
1
9
10
1
63
10
7
7
3
,
6
)
1
(
3
,
6
1
7
=
−
=
−
⋅
=
→
=
+
→
=
+
i
i
i
Zadanie 8
4
,
45
88
1
0483
,
0
7
0
≈
=
−
⋅
e
S
(
)
=
≈
−
⋅
⋅
=
≈
=
−
⋅
⋅
17
,
0
69
,
36
1
0483
,
0
37
,
0
7
exp
88
83
,
0
5
,
60
88
1
0483
,
0
85
,
1
7
1
p
p
e
S
(
)
(
)
(
)
=
≈
−
⋅
⋅
⋅
=
≈
−
⋅
⋅
⋅
=
≈
−
⋅
=
2
2
2
2
2
17
,
0
91
,
33
1
0483
,
0
37
,
0
7
exp
88
17
,
0
83
,
0
2
8
,
40
1
0483
,
0
37
,
0
85
,
1
7
exp
88
83
,
0
97
,
102
1
0483
,
0
85
,
1
7
exp
88
p
p
p
S
(
)
(
)
(
)
(
)
=
≈
−
⋅
⋅
⋅
=
≈
−
⋅
⋅
⋅
=
≈
−
⋅
⋅
=
≈
−
⋅
=
3
3
2
2
2
2
3
3
3
17
,
0
93
,
32
1
0483
,
0
37
,
0
7
exp
88
17
,
0
83
,
0
3
27
,
35
1
0483
,
0
37
,
0
85
,
1
7
exp
88
17
,
0
83
,
0
3
67
,
49
1
0483
,
0
37
,
0
85
,
1
7
exp
88
83
,
0
35
,
275
1
0483
,
0
85
,
1
7
exp
88
p
p
p
p
S
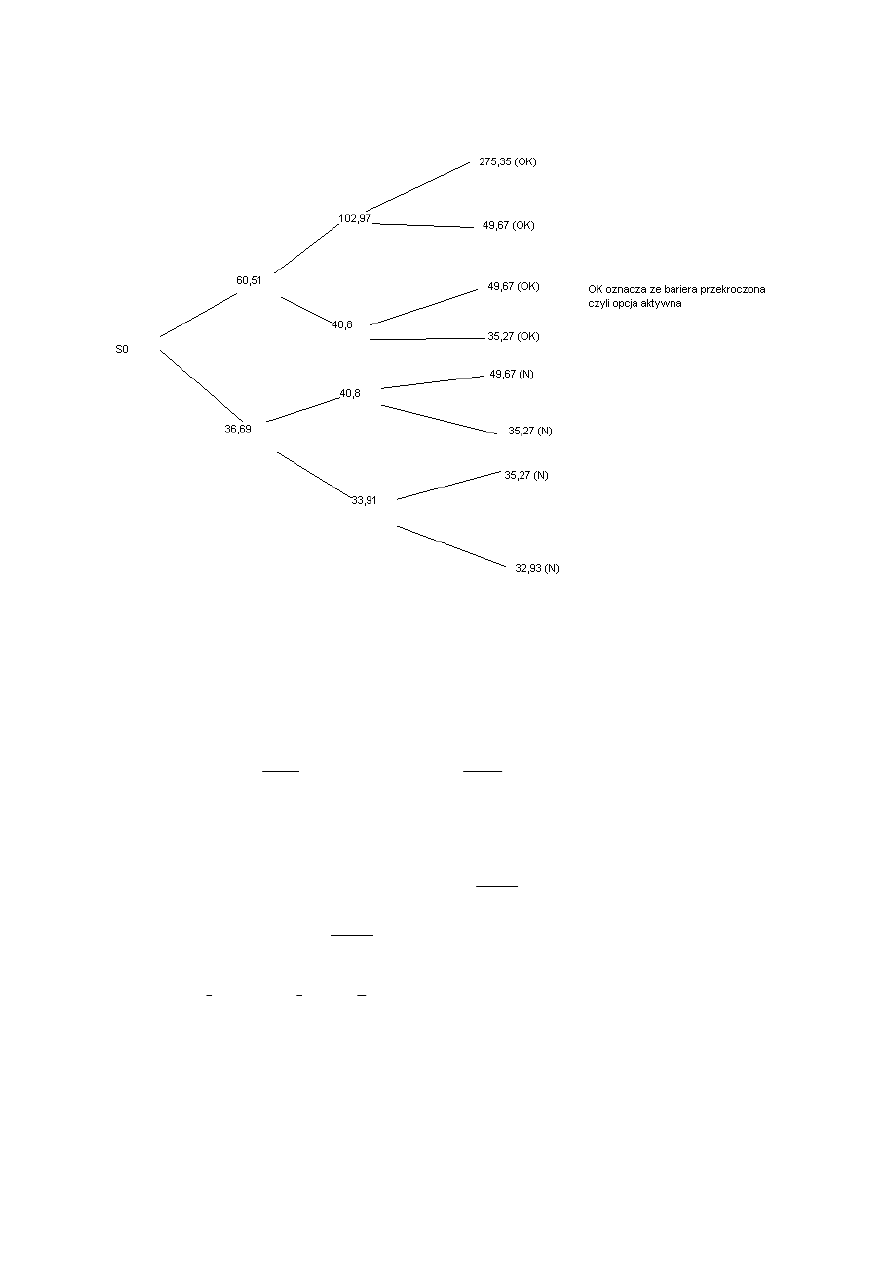
(
)
[
]
3
,
114
17
,
0
83
,
0
45
67
,
49
2
83
,
0
)
45
35
,
275
(
3
05
,
0
2
3
≈
−
+
−
≈
⋅
−
e
ODP
Najbliżej odpowiedź C
Zadanie 9
Odpowiedzi są w milionach i liczymy w milionach
Zgodnie ze wskazówką NAV
∆
to wartość bieżąca minus wartość po zmianie stopy
300
)
(
gdzie
)
(
)
(
)
(
)
(
=
′′
=
′
−
=
i
P
i
P
i
P
onvexity
effectivec
i
P
i
P
uration
effectived
CZ(w) – cena zobowiązania po wzroście stopy
CZ(s) – cena zobowiązania po spadku stopy
Z Taylora:
8105
,
259
3
,
2
300
2
03
,
0
5
,
4
300
)
05
,
0
08
,
0
(
300
)
(
2
=
⋅
⋅
+
⋅
⋅
−
−
=
w
CZ
8105
,
340
3
,
2
300
2
03
,
0
5
,
4
300
03
,
0
300
)
(
2
=
⋅
⋅
+
⋅
⋅
+
=
s
CZ
[
]
12
6
3
;
12
;
6
;
3
1
,
0
1
,
0
1
,
0
100
)
(
i
i
i
i
i
i
v
v
v
a
a
a
i
CA
+
+
+
+
+
⋅
=
65
,
13
300
)
(
)
08
,
0
(
)
05
,
0
(
=
−
+
−
=
∆
w
CZ
CA
CA
NAV
UP
→
<
−
+
−
=
∆
0
300
)
(
)
02
,
0
(
)
05
,
0
(
s
CZ
CA
CA
NAV
DOWN
odpowiedź B jest prawidłowa
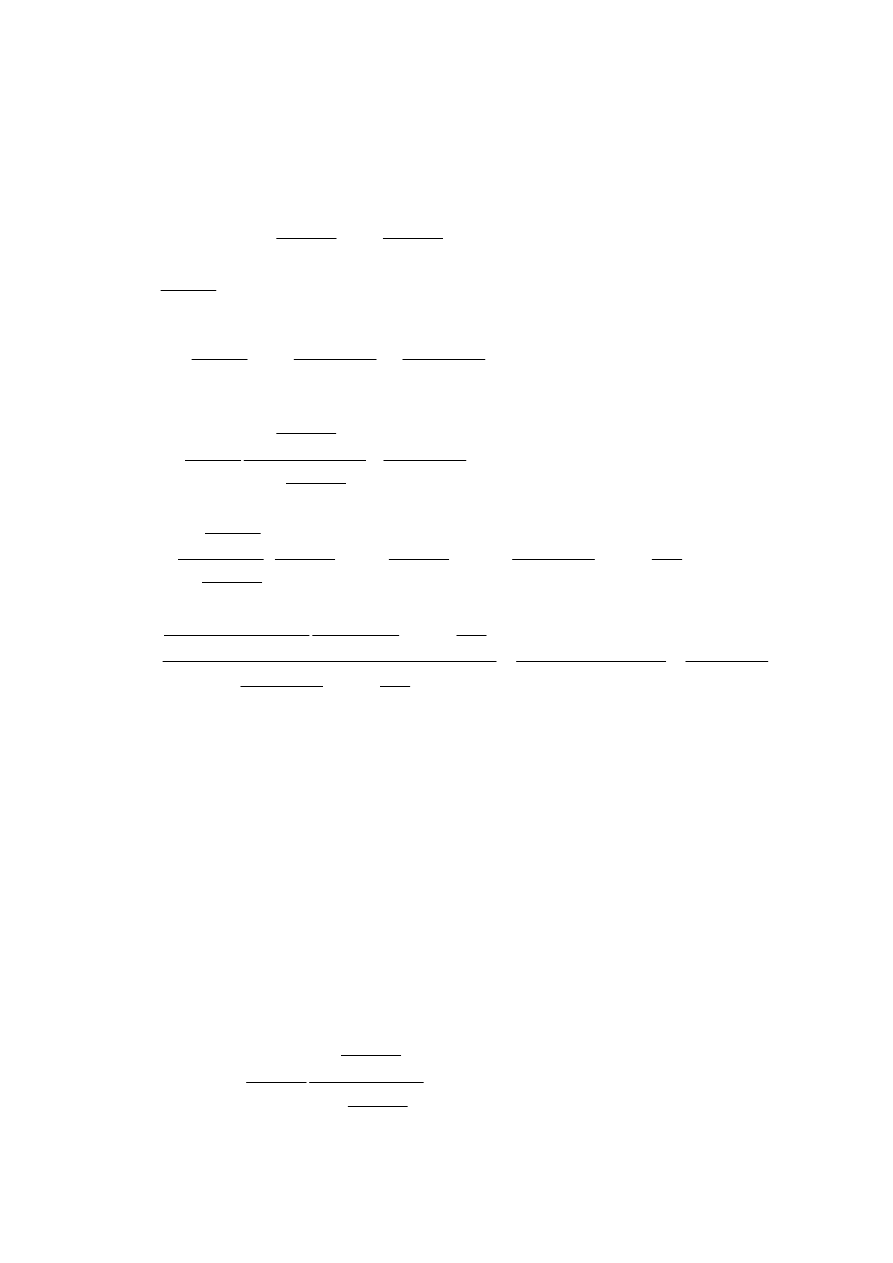
Zadanie 10
Pytanie powinno być jaką największą cenę (bo czym mniejsza cena tym większa
dochodowość)
1
04
,
1
gdzie
)
1
(
1
...
)
1
(
1
5
,
4
)
(
min
2
5
,
9
5
,
0
−
=
+
+
+
+
+
=
i
i
i
n
g
ODP
10
)
1
(
5
,
104
)
0
(
i
g
+
=
{
}
{
}
{
}
=
=
=
=
+
+
+
+
+
+
=
+
+
12
,
11
,
10
,
9
135
8
,
7
,
6
,
5
5
,
97
4
,
3
,
2
,
1
3
,
115
)
(
)
1
(
)
(
)
1
(
1
...
)
1
(
1
5
,
4
)
(
5
,
0
10
5
,
0
10
10
n
n
n
n
f
i
n
f
i
i
n
g
n
n
n
n
i
n
f
i
i
i
n
g
5
,
0
10
5
,
0
1
5
,
0
10
)
1
(
)
(
)
1
(
1
1
)
1
(
1
1
)
1
(
1
5
,
4
)
(
+
+
+
+
+
−
+
−
+
=
0
1
1
ln
5
,
0
)
1
(
1
)
(
)
1
(
1
ln
)
1
(
1
)
1
(
1
1
)
1
(
1
5
,
4
)
(
5
,
0
10
5
,
0
1
5
,
0
5
,
0
10
=
+
⋅
+
+
+
+
+
−
+
−
=
′
+
+
i
i
n
f
i
i
i
i
n
g
n
n
(
)
(
)
7
,
114
1
)
1
(
5
,
4
1
)
1
(
)
1
(
)
1
(
5
,
4
1
1
ln
5
,
0
)
1
(
1
1
1
ln
5
,
0
)
1
(
1
1
)
1
(
)
1
(
)
1
(
5
,
4
)
(
5
,
0
5
,
0
5
,
9
5
,
9
10
5
,
0
5
,
0
5
,
0
5
,
0
10
5
,
0
≈
−
+
=
−
+
+
+
=
+
⋅
+
+
⋅
+
−
+
+
+
=
+
+
i
i
i
i
i
i
i
i
i
i
i
n
f
n
n
7
,
114
)
(
dla
0
)
(
i
7
,
114
)
(
dla
0
)
(
>
>
′
<
<
′
→
n
f
n
g
n
f
n
g
{
}
{
}
{
}
)
9
(
)
(
min
12
,
11
,
10
,
9
dla
)
8
(
)
(
min
8
,
7
,
6
,
5
dla
)
1
(
)
(
min
4
,
3
,
2
,
1
dla
g
n
g
n
g
n
g
n
g
n
g
n
=
=
=
=
=
=
Porównujemy g(0), g(1), g(8), g(9)
61
,
60
)
9
(
4
,
48
)
8
(
63
,
54
)
1
(
69
,
47
)
0
(
≈
≈
≈
≈
g
g
g
g
8
,
106
)
1
(
1
1
)
1
(
1
1
)
1
(
1
5
,
4
69
,
47
5
,
0
19
5
,
0
5
,
0
≈
+
−
+
−
+
+
≈
i
i
i
ODP

Oznacza to, że płacąc 106,8 uzyskamy stopę 8% gdy obligacja zostanie wykupiona po 10
latach, a gdy później to stopa dochodowości będzie większa niż 8%
Wyszukiwarka
Podobne podstrony:
2010.10.04 matematyka finansowa
2010 10 04 matematyka finansowaid 27009
2011 06 20 matematyka finansowaid 27373
2011.06.20 matematyka finansowa
2011 06 20 matematyka finansowaid 27373
1 2009.04.06 matematyka finansowa
MATEMATYKA FINANSOWA WYKŁAD 3 (14 04 2012)
1 2000 04 08 matematyka finansowaid 8917
MATEMATYKA FINANSOWA ĆWICZENIA 4 (15 04 2012)
1 2009 04 06 matematyka finansowaid 8923
MATEMATYKA FINANSOWA ĆWICZENIA 4 (15 04 2012)
Complete Timeline of Darkest Powers Stories 2011 04 13
04 Zrodla finansowania dzialalnosci przedsiebiorstw zadania
więcej podobnych podstron